Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Determinants Ex 6.1 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 6 Determinants Ex 6.1
Question 1.
Evaluate the following determinants:


Solution:
(i) \(\left|\begin{array}{cc}
4 & 7 \\
-7 & 0
\end{array}\right|\)
= 4(0) – (-7)(7)
= 0 + 49
= 49
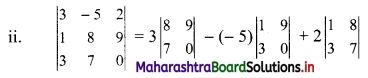
= 3(0 – 63) – 5(0 – 27) + 2(7 – 24)
= 3(-63) + 5 (-27) + 2(-17)
= – 189 – 135 – 34
= -358
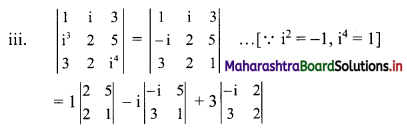
= 1(2 – 10) – i(-i – 15) + 3(-2i – 6)
= -8 + i2 + 15i – 6i – 18
= i2 – 26 + 9i
= -1 – 26 + 9i …[∵ i2 = -1]
= -27 + 9i
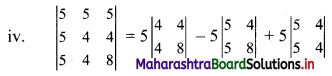
= 5(32 – 16) – 5(40 – 20) + 5(20 – 20)
= 5(16) – 5(20) + 5(0)
= 80 – 100
= -20
(v) \(\left|\begin{array}{cc}
2 \mathrm{i} & 3 \\
4 & -\mathrm{i}
\end{array}\right|\)
= 2i(-i) – 3(4)
= -2i2 – 12
= -2(-1) – 12 …[∵ i2 = -1]
= 2 – 12
= -10
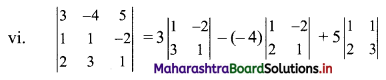
= 3(1 + 6) + 4(1 + 4) + 5(3 – 2)
= 3(7)+ 4(5) + 5(1)
= 21 + 20 + 5
= 46
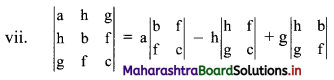
= a(bc – f2) – h(hc – gf) + g(hf – gb)
= abc – af2 – h2c + fgh + fgh – g2b
= abc + 2fgh – af2 – bg2 – ch2
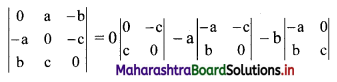
= 0 – a(0 + bc) – b(-ac – 0)
= -a(bc) – b(-ac)
= -abc + abc
= 0
![]()
Question 2.
Find the value(s) of x, if
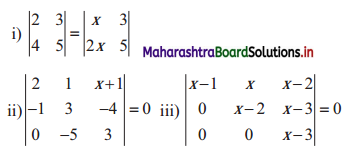
Solution:
(i) \(\left|\begin{array}{ll}
2 & 3 \\
4 & 5
\end{array}\right|=\left|\begin{array}{cc}
x & 3 \\
2 x & 5
\end{array}\right|\)
∴ 10 – 12 = 5x – 6x
∴ -2 = -x
∴ x = 2
Check:
We can check if our answer is right or wrong.
In order to do so, substitute x = 2 in the given determinant.
For x = 2,
L.H.S. = \(\left|\begin{array}{ll}
2 & 3 \\
4 & 5
\end{array}\right|\)
= 10 – 12
= -2
R.H.S. =\(\left|\begin{array}{cc}
x & 3 \\
2 x & 5
\end{array}\right|\)
= \(\left|\begin{array}{ll}
2 & 3 \\
4 & 5
\end{array}\right|\)
= 10 – 12
= -2
Thus, our answer is correct.
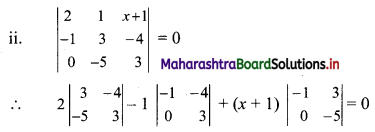
∴ 2(9 – 20) – 1 (-3 – 0) + (x + 1) (5 – 0) = 0
∴ 2(-11) – 1(-3) + (x + 1)(5) = 0
∴ -22 + 3 + 5x + 5 = 0
∴ 5x = 14
∴ x = \(\frac{14}{5}\)
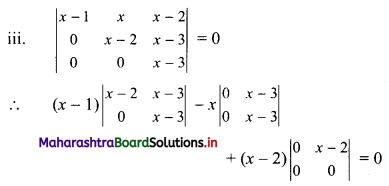
∴ (x – 1)[(x – 2)(x – 3) – 0] – x(0 – 0) + (x – 2)(0 – 0) = 0
∴ (x – 1)(x – 2)(x – 3) = 0
∴ x – 1 = 0 or x – 2 = 0 or x – 3 = 0
∴ x = 1 or x = 2 or x = 3
![]()
Question 3.
Solve the following equations.
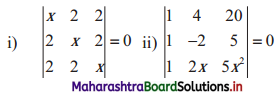
Solution:
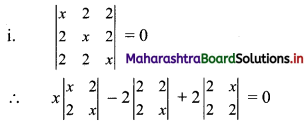
∴ x(x2 – 4) – 2(2x – 4) + 2(4 – 2x) = 0
∴ x(x2 – 4) – 2(2x – 4) – 2(2x – 4) = 0
∴ x(x + 2)(x – 2) – 4(2x – 4) = 0
∴ x(x + 2)(x – 2) – 8(x – 2) = 0
∴ (x – 2)[x(x + 2) – 8] = 0
∴ (x – 2)(x2 + 2x – 8) = 0
∴ (x – 2)(x2 + 4x – 2x – 8) = 0
∴ (x – 2)(x + 4)(x – 2) = 0
∴ (x – 2)2 (x + 4) = 0
∴ (x – 2)2 = 0 or x + 4 = 0
∴ x – 2 = 0 or x = -4
∴ x = 2 or x = -4
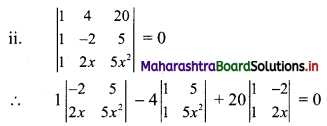
∴ 1(-10x2 – 10x) – 4(5x2 – 5) + 20(2x + 2) = 0
∴ -10x2 – 10x – 20x2 + 20 + 40x + 40 = 0
∴ -30x2 + 30x + 60 = 0
∴ x2 – x – 2 = 0 …..[Dividing throughout by (-30)]
∴ x2 – 2x + x – 2 = 0
∴ (x – 2)(x + 1) = 0
∴ x – 2 = 0 or x + 1 = 0 x = 2 or x = -1
![]()
Question 4.
Find the value of x, if
\(\left|\begin{array}{ccc}
x & -1 & 2 \\
2 x & 1 & -3 \\
3 & -4 & 5
\end{array}\right|\) = 29
Solution:
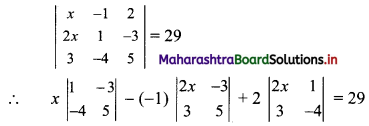
∴ x(5 – 12) + 1(10x + 9) + 2(-8x – 3) = 29
∴ -7x + 10x + 9 – 16x – 6 = 29
∴ -13x + 3 = 29
∴ -13x = 26
∴ x = -2
![]()
Question 5.
Find x and y if \(\left|\begin{array}{ccc}
4 i & i^{3} & 2 i \\
1 & 3 i^{2} & 4 \\
5 & -3 & i
\end{array}\right|\) = x + iy, where i = √-1.
Solution:

= 4i(-3i + 12) + i(i – 20) + 2i(-3 + 15)
= -12i2 + 48i + i2 – 20i + 24i
= -11i2 + 52i
= -11(-1) + 52i …..[∵ i2 = -1]
= 11 + 52i
Comparing with x + iy, we get
x = 11, y = 52