Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Determinants Ex 6.3 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 6 Determinants Ex 6.3
Question 1.
Solve the following equations using Cramer’s Rule.
(i) x + 2y – z = 5, 2x – y + z = 1, 3x + 3y = 8
Solution:
Given equations are
x + 2y – z = 5
2x – y + z = 1
3x + 3y = 8 i.e. 3x + 3y + 0z = 8
∴ D = \(\left|\begin{array}{ccc}
1 & 2 & -1 \\
2 & -1 & 1 \\
3 & 3 & 0
\end{array}\right|\)
= 1(0 – 3) – 2(0 – 3) – 1(6 + 3)
= -3 + 6 – 9
= -6
Dx = \(\left|\begin{array}{ccc}
5 & 2 & -1 \\
1 & -1 & 1 \\
8 & 3 & 0
\end{array}\right|\)
= 5(0 – 3) – 2(0 – 8) + (-1)(3 + 8)
= -15 + 16 – 11
= -10
Dy = \(\left|\begin{array}{ccc}
1 & 5 & -1 \\
2 & 1 & 1 \\
3 & 8 & 0
\end{array}\right|\)
= 1(0 – 8) – 5(0 – 3) + 1(16 – 3)
= -8 + 15 – 13
= -6
Dz = \(\left|\begin{array}{ccc}
1 & 2 & 5 \\
2 & -1 & 1 \\
3 & 3 & 8
\end{array}\right|\)
= 1(-8 – 3) – 2(16 – 3) + 5(6 + 3)
= -11 – 26 + 45
= 8
By Cramer’s Rule,

x = \(\frac{5}{3}\), y = 1 and z = \(\frac{-4}{3}\) are the solutions of the given equations.
Check:
We can check if our answer is right or wrong.
In order to do so, substitute the values of x, y and z in the given equations.
x = \(\frac{5}{3}\), y = 1 and z = \(\frac{-4}{3}\) satisfy the given equations.
If either one of the equations is not satisfied, then our answer is wrong.
If x = \(\frac{5}{3}\), y = 1 and z = \(\frac{-4}{3}\) are the solutions of the given equations.
L.H.S. = x + 2y – z
= \(\frac{5}{3}+2-\frac{4}{3}\)
= \(\frac{7}{3}\)
≠ R.H.S.
L.H.S. = 2x – y + z
= \(\frac{10}{3}-1+\frac{4}{3}\)
= \(\frac{11}{3}\)
≠ R.H.S.
L.H.S. = 3x + 3y
= 5 + 3
= 8
= R.H.S.
![]()
(ii) 2x – y + 6z = 10, 3x + 4y – 5z = 11, 8x – 7y – 9z = 12
Solution:
Given equations are
2x – y + 6z = 10
3x + 4y – 5z = 11
8x – 7y – 9z = 12
∴ D = \(\left|\begin{array}{ccc}
2 & -1 & 6 \\
3 & 4 & -5 \\
8 & -7 & -9
\end{array}\right|\)
= 2(-36 – 35) – (-1)(-27 + 40) + 6(-21 – 32)
= -142 + 13 – 318
= -447
Dx = \(\left|\begin{array}{ccc}
10 & -1 & 6 \\
11 & 4 & -5 \\
12 & -7 & -9
\end{array}\right|\)
= 10(-36 – 35) – (-1)(-99 + 60) + 6(-77 – 48)
= -710 – 39 – 750
= -1499
Dy = \(\left|\begin{array}{ccc}
2 & 10 & 6 \\
3 & 11 & -5 \\
8 & 12 & -9
\end{array}\right|\)
= 2(-99 + 60) – 10(-27 + 40) + 6(36 – 88)
= -78 – 130 – 312
= -520
Dz = \(\left|\begin{array}{ccc}
2 & -1 & 10 \\
3 & 4 & 11 \\
8 & -7 & 12
\end{array}\right|\)
= 2(48 + 77) – (-1)(36 – 88) + 10(-21 – 32)
= 250 – 52 – 530
= -332
By Cramer’s Rule,
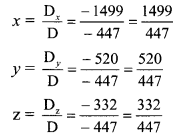
∴ x = \(\frac{1499}{447}\), y = \(\frac{520}{447}\) and z = \(\frac{332}{447}\) are the solutions of the given equations.
(iii) 11x – y – z = 31, x – 6y + 2z = -26, x + 2y – 7z = -24
Solution:
Given equations are
11x – y – z = 31
x – 6y + 2z = -26
x + 2y – 7z = -24
D = \(\left|\begin{array}{ccc}
11 & -1 & -1 \\
1 & -6 & 2 \\
1 & 2 & -7
\end{array}\right|\)
= 11(42 – 4) – (-1)(-7 – 2) + (-1)(2 + 6)
= 418 – 9 – 8
= 401
Dx = \(\left|\begin{array}{ccc}
31 & -1 & -1 \\
-26 & -6 & 2 \\
-24 & 2 & -7
\end{array}\right|\)
= 31(42 – 4) – (-1)(182 + 48) + (-1)(-52 – 144)
= 1178 + 230 + 196
= 1604
Dy = \(\left|\begin{array}{ccc}
11 & 31 & -1 \\
1 & -26 & 2 \\
1 & -24 & -7
\end{array}\right|\)
= 11(182 + 48) – 31(-7 – 2) + (-1)(-24 + 26)
= 2530 + 279 – 2
= 2807
Dz = \(\left|\begin{array}{ccc}
11 & -1 & 31 \\
1 & -6 & -26 \\
1 & 2 & -24
\end{array}\right|\)
= 11(144 + 52) – (-1)(-24 + 26) + 31(2 + 6)
= 2156 + 2 + 248
= 2406
By Cramer’s Rule,
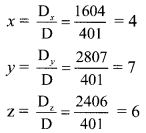
∴ x = 4, y = 7 and z = 6 are the solutions of the given equations.
![]()
(iv) \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=-2\), \(\frac{1}{x}-\frac{2}{y}+\frac{1}{z}=3\), \(\frac{2}{x}-\frac{1}{y}+\frac{3}{z}=-1\)
Solution:
Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r
The given equations become
p + q + r = -2
p – 2q + r = 3
2p – q + 3r = -1
D = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & -2 & 1 \\
2 & -1 & 3
\end{array}\right|\)
= 1(-6 + 1) – 1(3 – 2) + 1(-1 + 4)
= -5 – 1 + 3
= -3
Dp = \(\left|\begin{array}{rrr}
-2 & 1 & 1 \\
3 & -2 & 1 \\
-1 & -1 & 3
\end{array}\right|\)
= -2(-6 + 1) – 1(9 + 1) + 1(-3 – 2)
= 10 – 10 – 5
= -5
Dq = \(\left|\begin{array}{ccc}
1 & -2 & 1 \\
1 & 3 & 1 \\
2 & -1 & 3
\end{array}\right|\)
= 1(9 + 1) + 2(3 – 2) + 1(-1 – 6)
= 10 + 2 – 7
= 5
Dr = \(\left|\begin{array}{rrr}
1 & 1 & -2 \\
1 & -2 & 3 \\
2 & -1 & -1
\end{array}\right|\)
= 1(2 + 3) – 1(-1 – 6) – 2(-1 + 4)
= 5 + 7 – 6
= 6
By Cramer’s Rule,
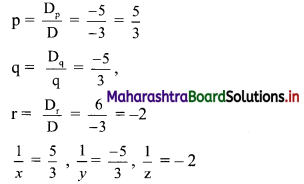
∴ x = \(\frac{3}{5}\), y = \(\frac{-3}{5}\), z = \(\frac{-1}{2}\) are the solutions of the given equations.
(v) \(\frac{2}{x}-\frac{1}{y}+\frac{3}{z}=4, \frac{1}{x}-\frac{1}{y}+\frac{1}{z}=2, \frac{3}{x}+\frac{1}{y}-\frac{1}{z}=2\)
Solution:
Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r
The given equations become
2p – q – 3r = 4
p – q + r = 2
3p + q – r = 2
D = \(\left|\begin{array}{ccc}
2 & -1 & 3 \\
1 & -1 & 1 \\
3 & 1 & -1
\end{array}\right|\)
= 2(1 – 1) – (-1)(-1 – 3) + 3(1 + 3)
= 0 – 4 + 12
= 8
Dp = \(\left|\begin{array}{ccc}
4 & -1 & 3 \\
2 & -1 & 1 \\
2 & 1 & -1
\end{array}\right|\)
= 4(1 – 1) – (-1)(-2 – 2) + 3(2 + 2)
= 0 – 4 + 12
= 8
Dq = \(\left|\begin{array}{ccc}
2 & 4 & 3 \\
1 & 2 & 1 \\
3 & 2 & -1
\end{array}\right|\)
= 2(-2 – 2) – 4(-1 – 3) + 3(2 – 6)
= -8 + 16 – 12
= -4
Dr = \(\left|\begin{array}{ccc}
2 & -1 & 4 \\
1 & -1 & 2 \\
3 & 1 & 2
\end{array}\right|\)
= 2(-2 – 2) – (-1)(2 – 6) + 4(1 + 3)
= -8 – 4 + 16
= 4
By Cramer’s Rule,
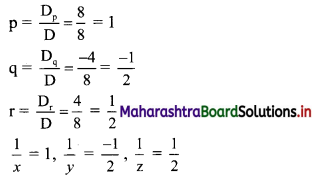
∴ x = 1, y = -2 and z = 2 are the solutions of the given equations.
![]()
Question 2.
An amount of ₹ 5,000 is invested in three plans at rates 6%, 7% and 8% per annum respectively. The total annual income from these investments is ₹ 350. If the total annual income from first two investments is ₹ 70 more than the income from the third, find the amount invested in each plan by using Cramer’s Rule.
Solution:
Let the amount of each investment be ₹ x, ₹ y and ₹ z.
According to the given conditions,
x + y + z = 5000
6%x + 7%y + 8%z = 350
∴ \(\frac{6}{100} x+\frac{7}{100} y-\frac{8}{100} z=350\)
∴ 6x + 7y + 8z = 35000
6%x + 7%y = 8%z + 70
∴ \(\frac{6}{100} x+\frac{7}{100} y=\frac{8}{100} z+70\)
∴ 6x + 7y = 8z + 7000
∴ 6x + 7y – 8z = 7000



∴ Amounts of investments are ₹ 1750, ₹ 1500, and ₹ 1750.
Check:
First condition:
1750 + 1500 + 1750 = 5000
Second condition:
6% of 1750 + 7% of 1500 + 8% of 1750
= 105 + 105 + 140
= 350
Third condition:
Combined income = 105 + 105
= 210
= 140 + 70
Thus, all the conditions are satisfied.
Question 3.
Show that the following equations are consistent.
2x + 3y + 4 = 0, x + 2y + 3 = 0, 3x + 4y + 5 = 0
Solution:
Given equations are
2x + 3y + 4 = 0
x + 2y + 3 = 0
3x + 4y + 5 = 0
∴ \(\left|\begin{array}{lll}
2 & 3 & 4 \\
1 & 2 & 3 \\
3 & 4 & 5
\end{array}\right|\)
= 2(10 – 12) – 3(5 – 9) + 4(4 – 6)
= 2(-2) – 3(-4) + 4(-2)
= -4 + 12 – 8
= 0
∴ The given equations are consistent.
![]()
Question 4.
Find k, if the following equations are consistent.
(i) x + 3y + 2 = 0, 2x + 4y – k = 0, x – 2y – 3k = 0
Solution:
Given equations are
x + 3y + 2 = 0
2x + 4y – k = 0
x – 2y – 3k = 0
Since, these equations are consistent.
∴ \(\left|\begin{array}{ccc}
1 & 3 & 2 \\
2 & 4 & -k \\
1 & -2 & -3 k
\end{array}\right|=0\)
∴ 1(-12k – 2k) – 3(-6k + k) + 2(-4 – 4) = 0
∴ -14k + 15k – 16 = 0
∴ k – 16 = 0
∴ k = 16
Check:
If the value of k satisfies the condition for the given equations to be consistent, then our answer is correct.
Substitute k = 16 in the given equation.
\(\left|\begin{array}{ccc}
1 & 3 & 2 \\
2 & 4 & -16 \\
1 & -2 & -48
\end{array}\right|\)
= 1(-192 – 32) – 3(-96 + 16) + 2(-4 – 4)
= 0
Thus, our answer is correct.
(ii) (k – 2)x + (k – 1)y = 17, (k – 1)x + (k – 2)y = 18, x + y = 5
Solution:
Given equations are
(k – 2)x + (k – 1)y = 17
(k – 1)x + (k – 2)y = 18
x + y = 5
Since, these equations are consistent.
∴ \(\left|\begin{array}{ccc}
k-2 & k-1 & -17 \\
k-1 & k-2 & -18 \\
1 & 1 & -5
\end{array}\right|=0\)
Applying R1 → R1 – R2, we get
\(\left|\begin{array}{ccc}
-1 & 1 & 1 \\
k-1 & k-2 & -18 \\
1 & 1 & -5
\end{array}\right|=0\)
∴ -1(-5k + 10 + 18) – 1(-5k + 5 + 18) + 1(k – 1 – k + 2) = 0
∴ -1(-5k – 28) – 1(- 5k + 23) + 1(1) = 0
∴ 5k – 28 + 5k – 23 – 1 = 0
∴ 10k – 50 = 0
∴ k = 5
Question 5.
Find the area of the triangle whose vertices are:
(i) (4, 5), (0, 7), (-1, 1)
Solution:
Here, A(x1, y1) ≡ A(4, 5), B(x2, y2) ≡ B(0, 7), C(x3, y3) ≡ C(-1, 1)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ A(ΔABC) = \(\frac{1}{2}\left|\begin{array}{ccc}
4 & 5 & 1 \\
0 & 7 & 1 \\
-1 & 1 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [4(7 – 1) – 5(0 + 1) + 1(0 + 7)]
= \(\frac{1}{2}\) (24 – 5 + 7)
= 13 sq.units.
(ii) (3, 2), (-1, 5), (-2, -3)
Solution:
Here, A(x1, y1) ≡ A(3, 2), B(x2, y2) = B(-1, 5), C(x3, y3) ≡ C(-2, -3)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ A(ΔABC) = \(\frac{1}{2}\left|\begin{array}{ccc}
3 & 2 & 1 \\
-1 & 5 & 1 \\
-2 & -3 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [3(5 + 3) – 2(-1 + 2) + 1(3 + 10)]
= \(\frac{1}{2}\) (24 – 2 + 13)
= \(\frac{35}{2}\) sq. units
![]()
(iii) (0, 5), (0, -5), (5, 0)
Solution:
Here, A(x1, y1) ≡ A(0, 5), B(x2, y2) ≡ B(0, -5), C(x3, y3) ≡ C(5,0)
Area of a triangle = \(\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ A(ΔABC) = \(\frac{1}{2}\left|\begin{array}{ccc}
0 & 5 & 1 \\
0 & -5 & 1 \\
5 & 0 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [0(-5 – 0) – 5(0 – 5) + 1(0 + 25)]
= \(\frac{1}{2}\) (0 + 25 + 25)
= \(\frac{50}{2}\)
= 25 sq.units
Question 6.
Find the value of k, if the area of the triangle with vertices at A(k, 3), B(-5, 7), C(-1, 4) is 4 square units.
Solution:
Here, A(x1, y1) ≡ A(k, 3), B(x2, y2) ≡ B(-5, 7), C(x3, y3) ≡ C(-1, 4)
A(ΔABC) = 4 sq.units
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{b} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ \(\frac{1}{2}\left|\begin{array}{ccc}
k & 3 & 1 \\
-5 & 7 & 1 \\
-1 & 4 & 1
\end{array}\right|\) = ±4
∴ k(7 – 4) – 3(-5 + 1) + 1(-20 + 7) = ±8
∴ 3k + 12 – 13 = ±8
∴ 3k – 1 = ±8
∴ 3k – 1 = 8 or 3k – 1 = -8
∴ 3k = 9 or 3k = -7
∴ k = 3 or k = \(\frac{-7}{3}\)
Check:
For k = 3,
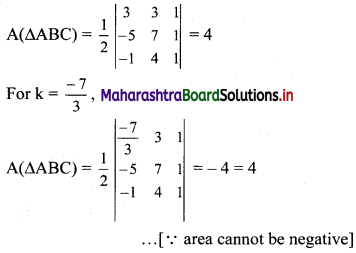
Thus, our answer is correct.
Question 7.
Find the area of the quadrilateral whose vertices are A(-3, 1), B(-2, -2), C(4, 1), D(2, 3).
Solution:
A(-3, 1), B(-2, -2), C(4, 1), D(2, 3)
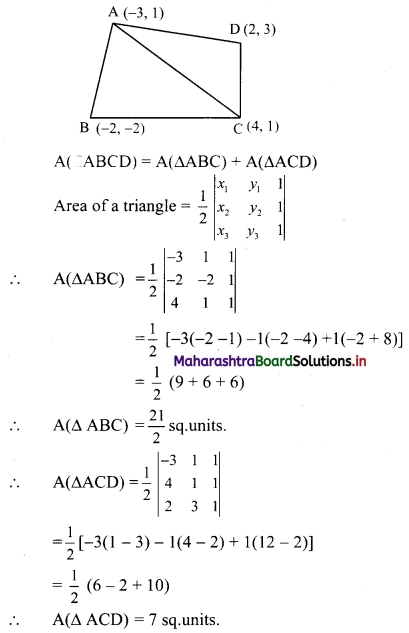
A(ABCD) = A(ΔABC) + A(ΔACD)
= \(\frac{21}{2}\) + 7
= \(\frac{35}{2}\) sq.units.
Question 8.
By using determinant, show that the following points are collinear.
P(5, 0), Q(10, -3), R(-5, 6)
Solution:
Here, P(x1, y1) ≡ P(5, 0), Q(x2, y2) ≡ Q(10, -3), R(x3, y3) ≡ R(-5, 6)
If A(ΔPQR) = 0, then the points P, Q, R are collinear.
∴ A(ΔPQR) = \(\frac{1}{2}\left|\begin{array}{ccc}
5 & 0 & 1 \\
10 & -3 & 1 \\
-5 & 6 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [5(-3 – 6) – 0(10 + 5) + 1(60 – 15)]
= \(\frac{1}{2}\) (-45 + 0 + 45)
= 0
∴ A(ΔPQR) = 0
∴ Points P, Q and R are collinear.
![]()
Question 9.
The sum of three numbers is 15. If the second number is subtracted from the sum of first and third numbers, then we get 5. When the third number is subtracted from the sum of twice the first number and the second number, we get 4. Find the three numbers.
Solution:
Let the three numbers be x, y and z.
According to the given conditions,
x + y + z = 15
x + z – y = 5 i.e. x – y + z = 5
2x + y – z = 4
D = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & -1 & 1 \\
2 & 1 & -1
\end{array}\right|\)
= 1(1 – 1) – 1 (-1 – 2) + 1(1 + 2)
= 1(0) – 1(-3) + 1(3)
= 0 + 3 + 3
= 6 ≠ 0
Dx = \(\left|\begin{array}{ccc}
15 & 1 & 1 \\
5 & -1 & 1 \\
4 & 1 & -1
\end{array}\right|\)
= 15(1 – 1) – 1(-5 – 4) + 1(5 + 4)
= 15(0) – 1(-9) + 1(9)
= 0 + 9 + 9
= 18
Dy = \(\left|\begin{array}{ccc}
1 & 15 & 1 \\
1 & 5 & 1 \\
2 & 4 & -1
\end{array}\right|\)
= 1(-5 – 4) – 15(-1 – 2) + 1(4 – 10)
= 1(-9) – 15(-3) + 1(-6)
= -9 + 45 – 6
= 30
Dz = \(\left|\begin{array}{ccc}
1 & 1 & 15 \\
1 & -1 & 5 \\
2 & 1 & 4
\end{array}\right|\)
= 1(-4 – 5) – 1(4 – 10) + 15(1 + 2)
= 1(-9) – 1(-6) + 15(3)
= -9 + 6 + 45
= 42
By Cramer’s Rule,
x = \(\frac{D_{x}}{D}=\frac{18}{6}\) = 3
y = \(\frac{D_{y}}{D}=\frac{30}{6}\) = 5
z = \(\frac{D_{z}}{D}=\frac{42}{6}\) = 7
∴ The three numbers are 3, 5 and 7.