Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Permutations and Combinations Ex 6.5 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 6 Permutations and Combinations Ex 6.5
Question 1.
In how many different ways can 8 friends sit around a table?
Solution:
We know that ‘n’ persons can sit around a table in (n – 1)! ways
∴ 8 friends can sit around a table in 7! ways
= 7 × 6 × 5 × 4 × 3 × 2 × 1
= 5040 ways.
∴ 8 friends can sit around a table in 5040 ways.
Question 2.
A party has 20 participants and a host. Find the number of distinct ways for the host to sit with them around a circular table. How many of these ways have two specified persons on either side of the host?
Solution:
A party has 20 participants.
All of them and the host (i.e., 21 persons) can be seated at a circular table in (21 – 1)! = 20! ways.
When two particular participants be seated on either side of the host.
Host takes chair in 1 way.
These 2 persons can sit on either side of host in 2! ways
Once host occupies his chair, it is not circular permutation any more.
Remaining 18 people occupy their chairs in 18! ways.
∴ Total number of arrangement possible if two particular participants be seated on either side of the host = 2! × 18!
![]()
Question 3.
Delegates from 24 countries participate in a round table discussion. Find the number of seating arrangements where two specified delegates are
(i) always together.
(ii) never together.
Solution:
(i) Delegates of 24 countries are to participate in a round table discussion such that two specified delegates are always together.
Let us consider these 2 delegates as one unit.
They can be arranged among themselves in 2! ways.
Also, these two delegates are to be seated with 22 other delegates (i.e. total 23) which can be done in (23 – 1)! = 22! ways.
∴ The total number of arrangements if two specified delegates are always together = 22! × 2!
(ii) When 2 specified delegates are never together then, the other 22 delegates can participate in a round table discussion in (22 – 1)! = 21! ways.
∴ There are 22 places of which any 2 places can be filled by those 2 delegates who are never together.
∴ Two specified delegates can be arranged in 22P2 ways.
∴ Total number of arrangements if two specified delegates are never together = 22P2 × 21!
= \(\frac{22 !}{(22-2) !}\) × 21!
= \(\frac{22 !}{20 !}\) × 21!
= 22 × 21 × 21!
= 21 × 22 × 21!
= 21 × 22!
Question 4.
Find the number of ways for 15 people to sit around the table so that no two arrangements have the same neighbours.
Solution:
There are 15 people to sit around a table.
∴ They can be arranged in (15 – 1)! = 14! ways.
But, they should not have the same neighbour in any two arrangements.
Around the table, arrangements (i.e. clockwise and anticlockwise) coincide.
∴ Number of arrangements possible for not to have same neighbours = \(\frac{14 !}{2}\)
Question 5.
A committee of 20 members sits around a table. Find the number of arrangements that have the president and the vice president together.
Solution:
A committee of 20 members sits around a table.
But, President and Vice-president sit together.
Let us consider President and Vice-president as one unit.
They can be arranged among themselves in 2! ways.
Now, this unit with the other 18 members of the committee is to be arranged around a table, which can be done in (19 – 1)! = 18! ways.
∴ The total number of arrangements possible if President and Vice-president sit together = 18! × 2!
![]()
Question 6.
Five men, two women, and a child sit around a table. Find the number of arrangements where the child is seated
(i) between the two women.
(ii) between two men.
Solution:
(i) 5 men, 2 women, and a child sit around a table
When a child is seated between two women
∴ The two women can be seated on either side of the child in 2! ways.
Let us consider these 3 (two women and a child) as one unit.
Also, these 3 are to be seated with 5 men, (i.e. a total of 6 units) which can be done in (6 – 1)! = 5! ways.
∴ The total number of arrangements if the child is seated between two women = 5! × 2!
(ii) Two men out of 5 men can sit on either side of the child in 5P2 ways.
Let us take two men and a child as one unit.
Now these are to be arranged with the remaining 3 men and 2 women
i.e., a total of 6 events (3 + 2 + 1) is to be arranged around a round table which can be done in (6 – 1)! = 5! ways.
∴ The total number of arrangements, if the child is seated between two men = 5P2 × 5!
Question 7.
Eight men and six women sit around a table. How many sitting arrangements will have no two women together?
Solution:
8 men can be seated around a table in (8 – 1)! = 7! ways.
There are 8 gaps created by 8 men’s seats.
∴ 6 Women can be seated in 8 gaps in 8P6 ways
∴ Total number of arrangements so that no two women are together = 7! × 8P6
Question 8.
Find the number of seating arrangements for 3 men and 3 women to sit around a table so that exactly two women are together.
Solution:
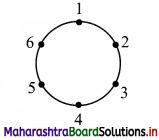
Two women sit together and one woman sits separately.
Women sitting separately can be selected in 3 ways.
The other two women occupy two chairs in one way (as it is a circular arrangement).
They can be seated on those two chairs in 2 ways. Suppose two chairs are chairs 1 and 2 shown in the figure.
Then the third woman has only two options viz chairs 4 or 5.
∴ The third woman can be seated in 2 ways. 3 men are seated in 3! ways
∴ Required number = 3 × 2 × 2 × 3!
= 12 × 6
= 72
Question 9.
Four objects in a set of ten objects are alike. Find the number of ways of arranging them in a circular order.
Solution:
Ten things can be arranged in a circular order of which 4 are alike in \(\frac{9 !}{4 !}\) ways.
∴ Required total number of arrangements = \(\frac{9 !}{4 !}\)
![]()
Question 10.
Fifteen persons sit around a table. Find the number of arrangements that have two specified persons not sitting side by side.
Solution:
Since 2 particular persons can’t be sitting side by side.
The other 13 persons can be arranged around the table in (13 – 1)! = 12!
13 people around a table create 13 gaps in which 2 people are to be seated
Number of arrangements of 2 people = 13P2
∴ The total number of arrangements in which two specified persons not sitting side by side = 12! × 13P2
= 12! × 13 × 12
= 13 × 12! × 12
= 12 × 13!