Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Permutations and Combinations Ex 6.7 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 6 Permutations and Combinations Ex 6.7
Question 1.
Find n if nC8 = nC12
Solution:
nC8 = nC12
If nCx = nCy, then either x = y or x = n – y
∴ 8 = 12 or 8 = n – 12
But 8 = 12 is not possible
∴ 8 = n – 12
∴ n = 20
Question 2.
Find n if 23C3n = 23C2n+3
Solution:
23C3n = 23C2n+3
If nCx = nCy, then either x = y or x = n – y
∴ 3n = 2n + 3 or 3n = 23 – 2n – 3
∴ n = 3 or n = 4
![]()
Question 3.
Find n if 21C6n = \({ }^{21} C_{n^{2}+5}\)
Solution:
21C6n = \({ }^{21} C_{n^{2}+5}\)
If nCx = nCy, then either x = y or x = n – y
∴ 6n = n2 + 5 or 6n = 21 – (n2 + 5)
∴ n2 – 6n + 5 = 0 or 6n = 21 – n2 – 5
∴ n2 – 6n + 5 = 0 or n2 + 6n – 16 = 0
If n2 – 6n + 5 = 0 then (n – 1)(n – 5) = 0
∴ n = 1 or n = 5
If n = 5 then n2 + 5 = 30 > 21
∴ n ≠ 5
∴ n = 1
If n2 + 6n – 16 = 0 then (n + 8)(n – 2) = 0
n = -8 or n = 2
n ≠ -8
∴ n = 2
Question 4.
Find n if 2nCr-1 = 2nCr+1
Solution:
2nCr-1 = 2nCr+1
If nCx = nCy, then either x = y or x = n – y
∴ r – 1 = r + 1 or r – 1 = 2n – (r + 1)
But r – 1 = r + 1 is not possible
∴ r – 1 = 2n – (r + 1)
∴ r + r = 2n
∴ r = n
Question 5.
Find n if nCn-2 = 15
Solution:
nCn-2 = 15
∴ nC2 = 15 …….[∵ nCr = nCn-r]
∴ \(\frac{n !}{(n-2) ! 2 !}\) = 15
∴ \(\frac{\mathrm{n}(\mathrm{n}-1)(\mathrm{n}-2) !}{(\mathrm{n}-2) ! 2 \times 1}\) = 15
∴ n(n – 1) = 30
∴ n(n – 1) = 6 × 5
Comparing both sides, we get
∴ n = 6
![]()
Question 6.
Find x if nPr = x nCr
Solution:
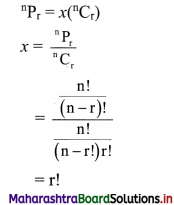
Question 7.
Find r if 11C4 + 11C5 + 12C6 + 13C7 = 14Cr
Solution:

Question 8.
Find the value of \(\sum_{r=1}^{4}{ }^{21-r} C_{4}+{ }^{17} C_{5}\)
Solution:

Question 9.
Find the differences between the largest values in the following:
(i) 14Cr – 12Cr
Solution:
Greatest value of 14Cr
Here n = 14, which is even
Greatest value of nCr occurs at r = \(\frac{n}{2}\) if n is even

∴ Difference between the greatest values of 14Cr and 12Cr = 3432 – 924 = 2508
(ii) 13Cr – 8Cr
Solution:
Greatest value of 13Cr
Here n = 13, which is odd
Greatest value of nCr occurs at r = \(\frac{\mathrm{n}-1}{2}\) if n is odd

∴ Difference between the greatest values of 13Cr and 8Cr = 1716 – 70 = 1646
(iii) 15Cr – 11Cr
Solution:
Greatest value of 15Cr
Here n = 15, which is odd
Greatest value of nCr occurs at r = \(\frac{\mathrm{n}-1}{2}\) if n is odd

Difference between the greatest values of 15Cr and 11Cr = 6435 – 462 = 5973
![]()
Question 10.
In how many ways can a boy invite his 5 friends to a party so that at least three join the party?
Solution:
Boy can invite = (3 or 4 or 5 friends)
Consider the following table:
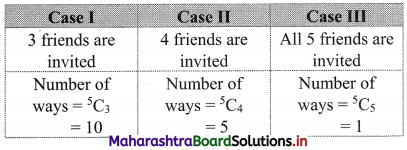
∴ Number of ways a boy can invite his friends to a party so that three or more join the party = 10 + 5 + 1 = 16
Question 11.
A group consists of 9 men and 6 women. A team of 6 is to be selected. How many possible selections will have at least 3 women?
Solution:
There are 9 men and 6 women.
A team of 6 persons is to be formed such that it consists of at least 3 women.
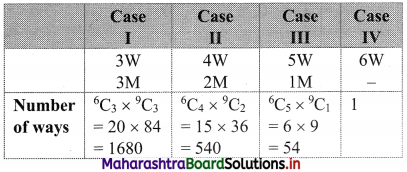
∴ Number of ways this can be done = 1680 + 540 + 54 + 1 = 2275
∴ 2275 teams can be formed if team consists of at least 3 women.
Question 12.
A committee of 10 persons is to be formed from a group of 10 women and 8 men. How many possible committees will have at least 5 women? How many possible committees will have men in the majority?
Solution:
(i) A committee of 10 persons is to be formed from 10 women and 8 men such that the committee contains at least 5 women
Consider the following table:
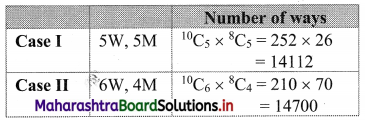
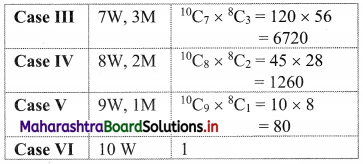
∴ Number of committees = 14112 + 14700 + 6720 + 1260 + 81 = 36873
∴ At least 5 women are there in 36873 committees.
(ii) Number of committees with men in majority = Total number of committees – (Number of committees with women in majority + women and men equal in number)
= 18C10 – 36873
= 18C8 – 36873
= 43758 – 36873
= 6885
![]()
Question 13.
A question paper has two sections. Section I has 5 questions and section II has 6 questions. A student must answer at least two questions from each section among 6 questions he answers. How many different choices does the student have in choosing questions?
Solution:
There are 11 questions, out of which 5 questions are from section I and 6 questions are from section II.
The student has to select 6 questions taking at least 2 questions from each section.
Consider the following table:

∴ Number of choices = 150 + 200 + 75 = 425
∴ In 425 ways students can select 6 questions, taking at least 2 questions from each section.
Question 14.
There are 3 wicketkeepers and 5 bowlers among 22 cricket players. A team of 11 players is to be selected so that there is exactly one wicketkeeper and at least 4 bowlers in the team. How many different teams can be formed?
Solution:
There are 22 cricket players, of which 3 are wicketkeepers and 5 are bowlers.
A team of 11 players is to be chosen such that exactly one wicketkeeper and at least 4 bowlers are to be included in the team.
Consider the following table:
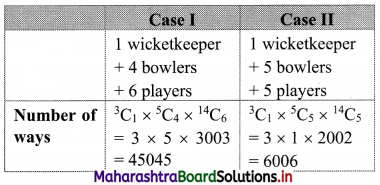
∴ Number of ways a team of 11 players can be selected = 45045 + 6006 = 51051
Question 15.
Five students are selected from 11. How many ways can these students be selected if
(i) two specified students are selected?
(ii) two specified students are not selected?
Solution:
5 students are to be selected from 11 students
(i) When 2 specified students are included
then remaining 3 students can be selected from (11 – 2) = 9 students.
∴ Number of ways of selecting 3 students from 9 students = 9C3
= \(\frac{9 !}{3 ! \times 6 !}\)
= \(\frac{9 \times 8 \times 7 \times 6 !}{3 \times 2 \times 1 \times 6 !}\)
= 84
∴ Selection of students is done in 126 ways when 2 specified students are not selected.
![]()
(ii) When 2 specified students are not included then 5 students can be selected from the remaining (11 – 2) = 9 students
∴ Number of ways of selecting 5 students from 9 students = 9C5
= \(\frac{9 !}{5 ! 4 !}\)
= \(\frac{9 \times 8 \times 7 \times 6 \times 5 !}{5 ! \times 4 \times 3 \times 2 \times 1}\)
= 126
∴ Selection of students is done in 126 ways when 2 specified students are not selected.