Maharashtra Board 11th Commerce Maths Solutions Chapter 7 Limits Miscellaneous Exercise 7

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 7 Limits Miscellaneous Exercise 7 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 7 Limits Miscellaneous Exercise 7

I.

Question 1.
If \(\lim _{x \rightarrow 2} \frac{x^{n}-2^{n}}{x-2}=80\) then find the value of n.
Solution:

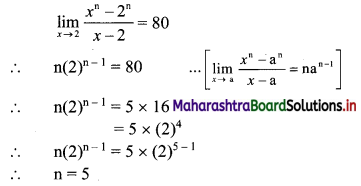
II. Evaluate the following Limits:

Question 1.
\(\lim _{x \rightarrow a} \frac{(x+2)^{\frac{5}{3}}-(a+2)^{\frac{5}{3}}}{x-a}\)
Solution:

Question 2.
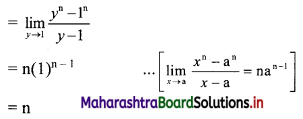
\(\lim _{x \rightarrow 0} \frac{(1+x)^{n}-1}{x}\)
Solution:

Question 3.
\(\lim _{x \rightarrow 2}\left[\frac{(x-2)}{2 x^{2}-7 x+6}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 1}\left[\frac{x^{3}-1}{x^{2}+5 x-6}\right]\)
Solution:

Question 5.
\(\lim _{x \rightarrow 3}\left[\frac{x-3}{\sqrt{x-2}-\sqrt{4-x}}\right]\)
Solution:

Question 6.
\(\lim _{x \rightarrow 4}\left[\frac{3-\sqrt{5+x}}{1-\sqrt{5-x}}\right]\)
Solution:

Question 7.
\(\lim _{x \rightarrow 0}\left[\frac{5^{x}-1}{x}\right]\)
Solution:

Question 8.
\(\lim _{x \rightarrow 0}\left(1+\frac{x}{5}\right)^{\frac{1}{x}}\)
Solution:

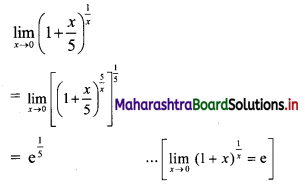
Question 9.
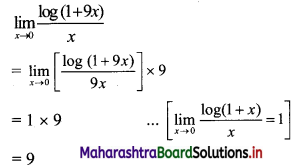
\(\lim _{x \rightarrow 0}\left[\frac{\log (1+9 x)}{x}\right]\)
Solution:

Question 10.
\(\lim _{x \rightarrow 0} \frac{(1-x)^{5}-1}{(1-x)^{3}-1}\)
Solution:

Question 11.
\(\lim _{x \rightarrow 0}\left[\frac{a^{x}+b^{x}+c^{x}-3}{x}\right]\)
Solution:

Question 12.
\(\lim _{x \rightarrow 0} \frac{e^{x}+e^{-x}-2}{x^{2}}\)
Solution:

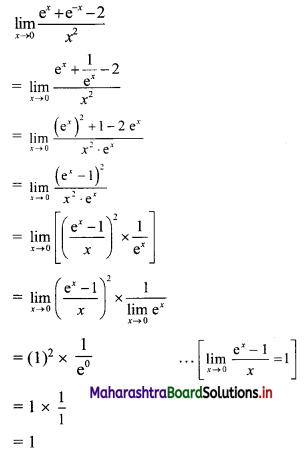
Question 13.
\(\lim _{x \rightarrow 0}\left[\frac{x\left(6^{x}-3^{x}\right)}{\left(2^{x}-1\right) \cdot \log (1+x)}\right]\)
Solution:

Question 14.
\(\lim _{x \rightarrow 0}\left[\frac{a^{3 x}-a^{2 x}-a^{x}+1}{x^{2}}\right]\)
Solution:

Question 15.
\(\lim _{x \rightarrow 0}\left[\frac{\left(5^{x}-1\right)^{2}}{x \cdot \log (1+x)}\right]\)
Solution:

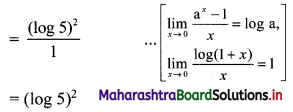
Question 16.
\(\lim _{x \rightarrow 0}\left[\frac{a^{4 x}-1}{b^{2 x}-1}\right]\)
Solution:

Question 17.
\(\lim _{x \rightarrow 0}\left[\frac{\log 100+\log (0.01+x)}{x}\right]\)
Solution:

Question 18.
\(\lim _{x \rightarrow 0}\left[\frac{\log (4-x)-\log (4+x)}{x}\right]\)
Solution:

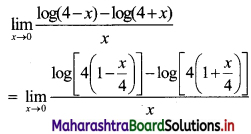
Question 19.
Evaluate the limit of the function if exist at x = 1 where,
\(f(x)= \begin{cases}7-4 x & x<1 \\ x^{2}+2 & x \geq 1\end{cases}\)
Solution: