Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 1 Complex Numbers Ex 1.2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 1 Complex Numbers Ex 1.2
Question 1.
Find the square root of the following complex numbers:
(i) -8 – 6i
Solution:
Let \(\sqrt{-8-6 i}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
-8 – 6i = (a + bi)2
-8 – 6i = a2 + b2i2 + 2abi
-8 – 6i = (a2 – b2) + 2abi …..[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = -8 and 2ab = -6

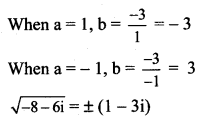
(ii) 7 + 24i
Solution:
Let \(\sqrt{7+24 i}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
7 + 24i = (a + bi)2
7 + 24i = a2 + b2i2 + 2abi
7 + 24i = (a2 – b2) + 2abi …..[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = 7 and 2ab = 24

![]()
(iii) 1 + 4√3 i
Solution:
Let \(\sqrt{1+4 \sqrt{3} i}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
1 + 4√3 i = (a + bi)2
1 + 4√3i = a2 + b2i2 + 2abi
1 + 4√3i = (a2 – b2) + 2abi …..[∵ i2 = -1]
Equating real arid imaginary parts, we get
a2 – b2 = 1 and 2ab = 4√3


(iv) 3 + 2√10 i
Solution:
Let \(\sqrt{3+2 \sqrt{10}} i\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
3 + 2√10 i = a2 + b2i2 + 2abi
3 + 2√10 i = (a2 – b2) + 2abi ……[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = 3 and 2ab = 2√10


(v) 2(1 – √3 i)
Solution:
Let \(\sqrt{2(1-\sqrt{3} i)}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
2(1 – √3 i) = a2 + b2i2 + 2abi
2 – 2√3 i = (a2 – b2) + 2abi ….[∵ i2 = -1]
Equating real and imaginary parts, we get
a2 – b2 = 2 and 2ab = -2√3
a2 – b2 = 2 and b = \(-\frac{\sqrt{3}}{a}\)

![]()
Question 2.
Solve the following quadratic equations:
(i) 8x2 + 2x + 1 = 0
Solution:
Given equation is 8x2 + 2x + 1 = 0
Comparing with ax2 + bx + c = 0, we get
a = 8, b = 2, c = 1
Discriminant = b2 – 4ac
= (2)2 – 4 × 8 × 1
= 4 – 32
= -28 < 0
So, the given equation has complex roots.
These roots are given by

(ii) 2x2 – √3 x + 1 = 0
Solution:
Given equation is 2x2 – √3 x + 1 = 0
Comparing with ax2 + bx + c = 0, we get
a = 2, b = -√3, c = 1
Discriminant = b2 – 4ac
= (-√3)2 – 4 × 2 × 1
= 3 – 8
= -5 < 0
So, the given equation has complex roots.
These roots are given by

(iii) 3x2 – 7x + 5 = 0
Solution:
Given equation is 3x2 – 7x + 5 = 0
Comparing with ax2 + bx + c = 0, we get
a = 3, b = -7, c = 5
Discriminant = b2 – 4ac
= (-7)2 – 4 × 3 × 5
= 49 – 60
= -11 < 0
So, the given equation has complex roots.
These roots are given by
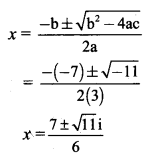
The roots of the given equation are \(\frac{7+\sqrt{11} \mathrm{i}}{6}\) and \(\frac{7-\sqrt{11} \mathrm{i}}{6}\)
![]()
(iv) x2 – 4x + 13 = 0
Solution:
Given equation is x2 – 4x + 13 = 0
Comparing with ax2 + bx + c = 0, we get
a = 1, b = -4, c = 13
Discriminant = b2 – 4ac
= (-4)2 – 4 × 1 × 13
= 16 – 52
= -36 < 0
So, the given equation has complex roots.
These roots are given by
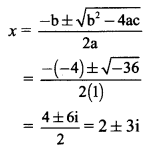
∴ The roots of the given equation are 2 + 3i and 2 – 3i.
Question 3.
Solve the following quadratic equations:
(i) x2 + 3ix + 10 = 0
Solution:
Given equation is x2 + 3ix + 10 = 0
Comparing with ax2 + bx + c = 0, we get
a = 1, b = 3i, c = 10
Discriminant = b2 – 4ac
= (3i)2 – 4 × 1 × 10
= 9i2 – 40
= -9 – 40 ……[∵ i2 = -1]
= -49 < 0
So, the given equation has complex roots.
These roots are given by

∴ x = 2i or x = -5i
∴ The roots of the given equation are 2i and -5i.
(ii) 2x2 + 3ix + 2 = 0
Solution:
Given equation is 2x2 + 3ix + 2 = 0
Comparing with ax + bx + c = 0, we get
a = 2, b = 3i, c = 2
Discriminant = b2 – 4ac
= (3i)2 – 4 × 2 × 2
= 9i2 – 16
= -9 – 16 …..[∵ i2 = -1]
= -25 < 0
So, the given equation has complex roots.
These roots are given by

∴ The roots of the given equation are \(\frac{1}{2}\)i and -2i.
![]()
(iii) x2 + 4ix – 4 = 0
Solution:
Given equation is x2 + 4ix – 4 = 0
Comparing with ax2 + bx + c = 0, we get
a = 1, b = 4i, c = -4
Discriminant = b2 – 4ac
= (4i)2 – 4 × 1 × (-4)
= 16i2 + 16
= -16 + 16 …..[∵ i2 = -1]
= 0
So, the given equation has equal roots.
These roots are given by
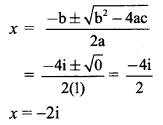
∴ x = -2i
∴ The root of the given equation is -2i.
(iv) ix2 – 4x – 4i = 0
Solution:
ix2 – 4x – 4i = 0
Multiplying throughout by i, we get
i2x2 – 4ix – 4i2 = 0
-x2 – 4ix + 4 = 0 …[∵ i2 = -1]
x2 + 4ix – 4 = 0
Comparing with ax2 + bx + c = 0, we get
a = 1, b = 4i, c = -4
Discriminant = b2 – 4ac
= (4i)2 – 4 × 1 × (-4)
= 16i2 + 16
= -16 + 16
= 0
So, the given equation has equal roots.
These roots are given by

∴ The root of the given equation is -2i
![]()
Question 4.
Solve the following quadratic equations:
(i) x2 – (2 + i) x – (1 – 7i) = 0
Solution:
Given equation is x2 – (2 + i)x – (1 – 7i) = 0
Comparing with ax2 + bx + c = 0, we get
a = 1, b = -(2 + i), c = -(1 – 7i)
Discriminant = b2 – 4ac
= [-(2 + i)]2 – 4 × 1 × -(1 – 7i)
= 4 + 4i + i2 + 4 – 28i
= 4 + 4i – 1 + 4 – 28i …..[∵ i2 = – 1]
= 7 – 24i
So, the given equation has complex roots.
These roots are given by
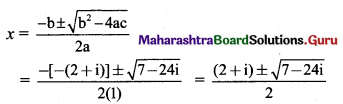
Let \(\sqrt{7-24 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
7 – 24i = a2 + i2b2 + 2abi
7 – 24i = a2 – b2 + 2abi
Equating real and imaginary parts, we get
a2 – b2 = 7 and 2ab = -24

(ii) x2 – (3√2 + 2i) x + 6√2 i = 0
Solution:
Given equation is x2 – (3√2 + 2i) x + 6√2 i = 0
Comparing with ax2 + bx + c = 0, we get
a = 1, b = -(3√2 + 2i), c = 6√2i
Discriminant = b2 – 4ac
= [-(3√2 + 2i)]2 – 4 × 1 × 6√2 i
= 18 + 12√2i + 4i2 – 24√2 i
= 18 – 12√2 i – 4 ……[∵ i2 = -1]
= 14 – 12√2 i
So, the given equation has complex roots.
These roots are given by



![]()
(iii) x2 – (5 – i) x + (18 + i) = 0
Solution:
Given equation is x2 – (5 – i)x + (18 + i) = 0
Comparing with ax2 + bx + c = 0, we get
a = 1, b = -(5 – i), c = 18 + i
Discriminant = b2 – 4ac
= [-(5 – i)]2 – 4 × 1 × (18 + i)
= 25 – 10i + i2 – 72 – 4i
= 25 – 10i – 1 – 72 – 4i ……[∵ i2 = -1]
= -48 – 14i
So, the given equation has complex roots.
These roots are given by


(iv) (2 + i) x2 – (5 – i) x + 2(1 – i) = 0
Solution:
Given equation is (2 + i) x2 – (5 – i) x + 2(1 – i) = 0
Comparing with ax2 + bx + c = 0, we get
a = 2 + i, b = -(5 – i), c = 2(1 – i)
Discriminant = b2 – 4ac
= [-(5 – i)]2 – 4 × (2 + i) × 2(1 – i)
= 25 – 10i + i2 – 8(2 + i) (1 – i)
= 25 – 10i + i2 – 8(2 – 2i + i – i2)
= 25 – 10i – 1 – 8(2 – i + 1) …..[∵ i2 = -1]
= 25 – 10i – 1 – 16 + 8i – 8
= -2i
So, the given equation has complex roots.
These roots are given by
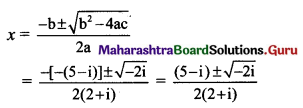
Let \(\sqrt{-2 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
-2i = a2 + b2i2 + 2abi
-2i = a2 – b2 + 2abi
Equating real and imaginary parts, we get
a2 – b2 = 0 and 2ab = -2
a2 – b2 = 0 and b = \(-\frac{1}{a}\)


![]()
Question 5.
Find the value of
(i) x3 – x2 + x + 46, if x = 2 + 3i
Solution:
x = 2 + 3i
x – 2 = 3i
(x – 2)2 = 9i2
x2 – 4x + 4 = 9(-1) …..[∵ i2 = -1]
x2 – 4x + 13 = 0 …..(i)

Dividend = Divisor × Quotient + Remainder
∴ x3 – x2 + x + 46 = (x2 – 4x + 13) (x + 3) + 7
= 0(x + 3) + 7 …..[from(i)]
= 7
Alternate Method:
x = 2 + 3i
α = 2 + 3i, \(\bar{\alpha}\) = 2 – 3i
α\(\bar{\alpha}\) = (2 + 3i)(2 – 3i)
= 4 – 6i + 6i – 9i2
= 4 – 9(-1)
= 4 + 9
= 13
α + \(\bar{\alpha}\) = 2 + 3i + 2 – 3i = 4
∴ Standard form of quadratic equation,
x2 – (Sum of roots) x + Product of roots = 0
x2 – 4x + 13 = 0

Dividend = Divisor × Quotient + Remainder
∴ x3 – x2 + x + 46 = (x2 – 4x + 13).(x + 3) + 7
= 0(x + 3) + 7 …..[From (i)]
= 7
(ii) 2x3 – 11x2 + 44x + 27, if x = \(\frac{25}{3-4 i}\)
Solution:


Dividend = Divisor × Quotient + Remainder
2x3 – 11x2 + 44x + 27 = (x2 – 6x + 25)(2x + 1) + 2
= 0.(2x + 1) + 2 …..[From (i)]
= 0 + 2
= 2
![]()
(iii) x3 + x2 – x + 22, if x = \(\frac{5}{1-2 i}\)
Solution:

Dividend = Divisor × Quotient + Remainder
x3 + x2 – x + 22 = (x2 – 2x + 5)(x + 3) + 7
= 0.(x + 3) + 7 …..[From (i)]
= 0 + 7
= 7
(iv) x4 + 9x3 + 35x2 – x + 4, if x = -5 + √-4
Solution:
x = -5 + √-4
x + 5 = √-4
x + 5 = √4 √-1
x + 5 = 2i
(x + 5)2 = 4i2
x2 + 10x + 25 = 4(-1) ….[∵ i2 = -1]
x2 + 10x + 29 = 0 …..(i)

Dividend = Divisor × Quotient + Remainder
x4 + 9x3 + 35x2 – x + 4 = (x2 + 10x + 29) (x2 – x + 16) – 132x – 460
= 0.(x2 – x + 16) – 132x – 460 …..[From (i)]
= -132 (-5 + 2i) – 460
= 660 – 264i – 460
= 200 – 264i
![]()
(v) 2x4 + 5x3 + 7x2 – x + 41, if x = -2 – √3i
Solution:
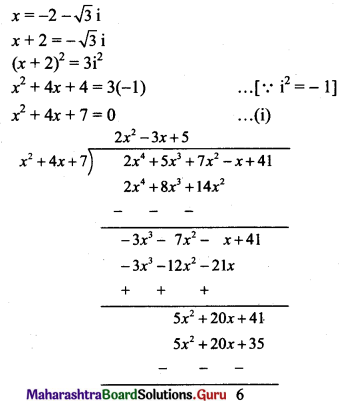
Dividend = Divisor × Quotient + Remainder
2x4 + 5x3 + 7x2 – x + 41 = (x2 + 4x + 7) (2x2 – 3x + 5) + 6
= 0(2x2 – 3x + 5) + 6 ……[From (i)]
= 0 + 6
= 6