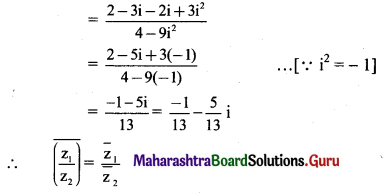Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 1 Complex Numbers Ex 1.3 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 1 Complex Numbers Ex 1.3
Question 1.
Find the modulus and amplitude for each of the following complex numbers:
(i) 7 – 5i
Solution:
Let z = 7 – 5i
a = 7, b = -5
i.e. a > 0, b < 0
|z| = \(\sqrt{a^{2}+b^{2}}=\sqrt{7^{2}+(-5)^{2}}=\sqrt{49+25}=\sqrt{74}\)
Here, (7, -5) lies in 4th quadrant.

(ii) √3 + √2 i
Solution:
Let z = √3 + √2 i
a = √3, b = √2,
i.e. a > 0, b > 0

![]()
(iii) -8 + 15i
Solution:
Let z = -8 + 15i
a = -8, b = 15 , i.e. a < 0, b > 0

(iv) -3(1 – i)
Solution:
Let z = -3(1 – i) = -3 + 3i
a = -3, b = 3 , i.e. a < 0, b > 0
|z| = \(\sqrt{a^{2}+b^{2}}=\sqrt{(-3)^{2}+3^{2}}=\sqrt{9+9}\) = 3√2
Here, (-3, 3) lies in 2nd quadrant.
amp(z) = π – \(\tan ^{-1}\left|\frac{b}{a}\right|\)
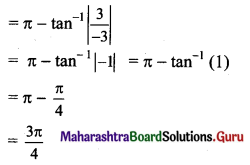
(v) -4 – 4i
Solution:
Let z = -4 – 4i
a = -4, b = -4 , i.e. a < 0, b < 0
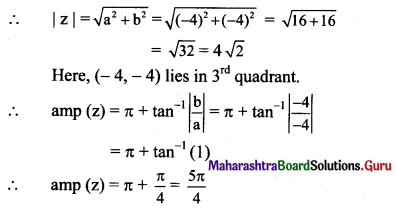
(vi) √3 – i
Solution:
Let z = √3 – i
a = √3, b = -1, i.e. a > 0, b < 0
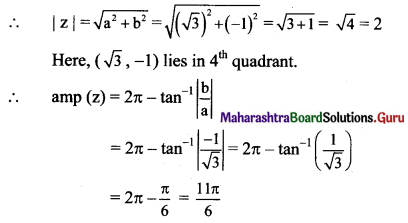
(vii) 3
Solution:
Let z = 3 + 0i
a = 3, b = 0
z is a real number, it lies on the positive real axis.
|z|= \(\sqrt{a^{2}+b^{2}}=\sqrt{3^{2}+0^{2}}=\sqrt{9+0}\) = 3
and amp (z) = 0
![]()
(viii) 1 + i
Solution:
Let z = 1 + i
a = 1, b = 1, i.e. a > 0, b > 0
|z| = \(\sqrt{a^{2}+b^{2}}=\sqrt{1^{2}+1^{2}}=\sqrt{1+1}=\sqrt{2}\)
Here, (1, 1) lies in 1st quadrant.
amp (z) = \(\tan ^{-1}\left(\frac{b}{a}\right)=\tan ^{-1}(1)=\frac{\pi}{4}\)
(ix) 1 + i√3
Solution:
Let z = 1 + i√3
a = 1, b = √3, i.e. a > 0, b > 0
|z| = \(\sqrt{a^{2}+b^{2}}=\sqrt{1^{2}+(\sqrt{3})^{2}}=\sqrt{1+3}=2\)
Here, (1, √3) lies in 1st quadrant.
amp (z) = \(\tan ^{-1}\left(\frac{b}{a}\right)=\tan ^{-1}(\sqrt{3})=\frac{\pi}{3}\)
(x) (1 + 2i)2 (1 – i)
Solution:
Let z = (1 + 2i)2 (1 – i)
= (1 + 4i + 4i2) (1 – i)
= [1 + 4i + 4(-1)] (1 – i) ….[∵ i2 = -1]
= (-3 + 4i) (1 – i)
= -3 + 3i + 4i – 4i2
= -3 + 7i – 4(-1)
= -3 + 7i + 4
∴ z = 1 + 7i
∴ a = 1, b = 7, i. e. a > 0, b > 0
∴ |z| = \(\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}=\sqrt{1^{2}+7^{2}}=\sqrt{1+49}=5 \sqrt{2}\)
Here, (1, 7) lies in 1st quadrant.
∴ amp(z) = \(\tan ^{-1}\left(\frac{b}{a}\right)=\tan ^{-1}(7)\)
Question 2.
Find real values of θ for which \(\left(\frac{4+3 i \sin \theta}{1-2 i \sin \theta}\right)\) is purely real.
Solution:

![]()
Question 3.
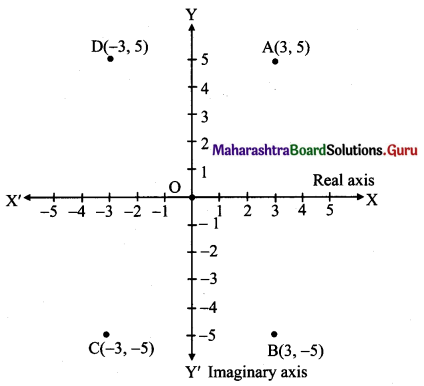
If z = 3 + 5i, then represent the z, \(\overline{\mathbf{z}}\), -z, \(\overline{\mathbf{-z}}\) in Argand’s diagram.
Solution:
z = 3 + 5i
\(\overline{\mathbf{z}}\) = 3 – 5i
-z = – 3 – 5i
\(\overline{\mathbf{-z}}\)= -3 + 5i
The above complex numbers will be represented by the points
A (3, 5), B (3, -5), C (-3, -5) , D (-3, 5) respectively as shown below:
Question 4.
Express the following complex numbers in polar form and exponential form.
(i) -1 + √3 i
Solution:
Let z = – 1 + √3
a = -1, b = √3

(ii) -i
Solution:
Let z = -i = 0 – i
a = 0, b = -1
z lies on negative imaginary Y-axis.
|z| = r = \(\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}=\sqrt{0^{2}+(-1)^{2}}\) = 1 and
θ = amp z = 270° = \(\frac{3 \pi}{2}\)
The polar form of z = r (cos θ + i sin θ)
= 1 (cos 270° + i sin 270°)
= 1 (cos \(\frac{3 \pi}{2}\) + i sin \(\frac{3 \pi}{2}\))
The exponential form of z = \(r e^{i \theta}=e^{\frac{3 \pi}{2} i}\)
(iii) -1
Solution:
Let z = -1 = -1 + 0.i
a = -1, b = 0
z lies on negative real X-axis.
|z| = r = \(\sqrt{a^{2}+b^{2}}=\sqrt{(-1)^{2}+0^{2}}\) = 1 and
θ = amp z = 180° = π
The polar form of z = r (cos θ + i sin θ)
= 1 (cos 180° + i sin 180°)
= 1 (cos π + i sin π)
The exponential form of z = \(r e^{i \theta}=e^{\pi i}\)
![]()
(iv) \(\frac{1}{1+i}\)
Solution:



(v) \(\frac{1+2 i}{1-3 i}\)
Solution:


(vi) \(\frac{1+7 \mathbf{i}}{(2-\mathbf{i})^{2}}\)
Solution:


![]()
Question 5.
Express the following numbers in the form x + iy:
(i) \(\sqrt{3}\left(\cos \frac{\pi}{6}+i \sin \frac{\pi}{6}\right)\)
Solution:

(ii) \(\sqrt{2} \cdot\left(\cos \frac{7 \pi}{4}+i \sin \frac{7 \pi}{4}\right)\)
Solution:

(iii) \(7\left(\cos \left(-\frac{5 \pi}{6}\right)+i \sin \left(-\frac{5 \pi}{6}\right)\right)\)
Solution:

(iv) \(e^{\frac{\pi}{3} i}\)
Solution:

(v) \(e^{\frac{-4 \pi}{3} i}\)
Solution:


![]()
(vi) \([latex]e^{\frac{5 \pi}{6} i}\)[/latex]
Solution:
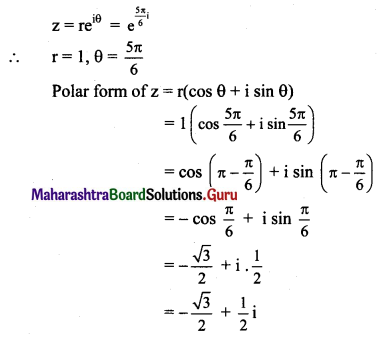
Question 6.
Find the modulus and argument of the complex number \(\frac{1+2 i}{1-3 i}\).
Solution:
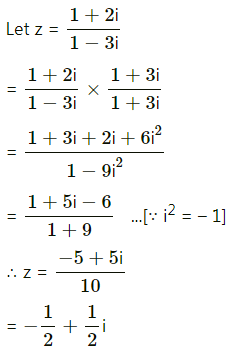

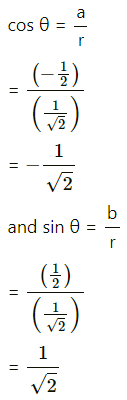
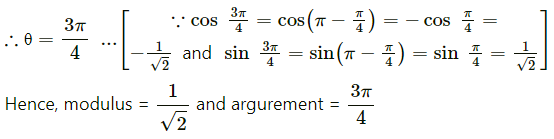
Question 7.
Convert the complex number \(\mathrm{z}=\frac{i-1}{\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}}\) in the polar form.
Solution:


![]()
Question 8.
For z = 2 + 3i, verify the following:
(i) \(\overline{(\bar{z})}=z\)
Solution:
z = 2 + 3i
∴ \(\bar{z}\) = 2 – 3i
∴ \(\overline{\bar{z}}\) = 2 + 3i = z
(ii) \(\overline{z \bar{z}}=|z|^{2}\)
Solution:
z\(\bar{z}\) = (2 + 3i) (2 – 3i)
= 4 – 9i2
= 4 – 9(-1) …..[∵ i2 = -1]
= 13
|z|2 = \(\left(\sqrt{2^{2}+3^{2}}\right)^{2}\)
= 22 + 32
= 4 + 9
= 13
∴ \(\overline{z \bar{z}}=|z|^{2}\)
(iii) (z + \(\bar{z}\)) is real
Solution:
(z + \(\bar{z}\)) = (2 + 3i) + (2 – 3i)
= 2 + 3i + 2 – 3i
= 4, which is a real number.
∴ z + \(\bar{z}\) is real.
(iv) z – \(\bar{z}\) = 6i
Solution:
z – \(\bar{z}\) = (2 + 3i) – (2 – 3i)
= 2 + 3i – 2 + 3i
= 6i
![]()
Question 9.
z1 = 1 + i, z2 = 2 – 3i, verify the following:
(i) \(\overline{Z_{1}+Z_{2}}=\overline{Z_{1}}+\overline{Z_{2}}\)
Solution:
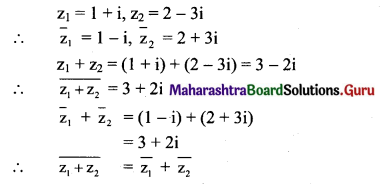
(ii) \(\overline{Z_{1}-Z_{2}}=\overline{Z_{1}}-\overline{Z_{2}}\)
Solution:
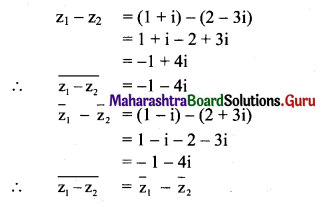
(iii) \(\overline{Z_{1} \cdot Z_{2}}=\overline{Z_{1}} \cdot \overline{Z_{2}}\)
Solution:

![]()
(iv) \(\overline{\left(\frac{\mathbf{z}_{1}}{\mathbf{z}_{2}}\right)}=\frac{\overline{\mathbf{z}}_{1}}{\overline{\mathbf{z}}_{2}}\)
Solution: