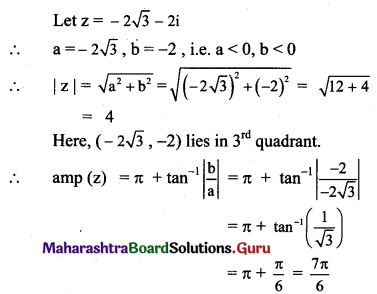Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 1 Complex Numbers Ex 1.4 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 1 Complex Numbers Ex 1.4
Question 1.
Find the value of
(i) ω18
(ii) ω21
(iii) ω-30
(iv) ω-105
Solution:

Question 2.
If ω is the complex cube root of unity, show that
(i) (2 – ω)(2 – ω2) = 7
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
L.H.S. = (2 – ω)(2 – ω2)
= 4 – 2ω2 – 2ω + ω3
= 4 – 2(ω2 + ω) + 1
= 4 – 2(-1) + 1
= 4 + 2 + 1
= 7
= R.H.S.
![]()
(ii) (1 + ω – ω2)6 = 64
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1

(iii) (1 + ω)3 – (1 + ω2)3 = 0
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
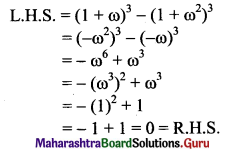
(iv) (2 + ω + ω2)3 – (1 – 3ω + ω2)3 = 65
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1

(v) (3 + 3ω + 5ω2)6 – (2 + 6ω + 2ω2)3 = 0
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
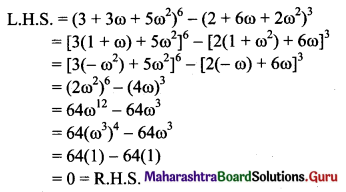
![]()
(vi) \(\frac{a+b \omega+c \omega^{2}}{c+a \omega+b \omega^{2}}\) = ω2
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1

(vii) (a + b) + (aω + bω2) + (aω2 + bω) = 0
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
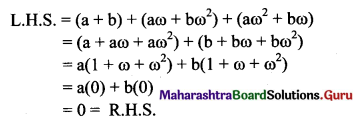
(viii) (a – b)(a – bω)(a – bω2) = a3 – b3
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1

(ix) (a + b)2 + (aω + bω2)2 + (aω2+ bω)2 = 6ab
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1

Question 3.
If ω is the complex cube root of unity, find the value of
(i) ω + \(\frac{1}{\omega}\)
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
\(\omega+\frac{1}{\omega}=\frac{\omega^{2}+1}{\omega}=\frac{-\omega}{\omega}=-1\)
(ii) ω2 + ω3 + ω4
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
ω2 + ω3 + ω4
= ω2(1 + ω + ω2)
= ω2(0)
= 0
![]()
(iii) (1 + ω2)3
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
(1 + ω2)3
= (-ω)3
= -ω3
= -1
(iv) (1 – ω – ω2)3 + (1 – ω + ω2)3
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
(1 – ω – ω2)3 + (1 – ω + ω2)3
= [1 – (ω + ω2)]3 + [(1 + ω2) – ω]3
= [1 – (-1)]2 + (-ω – ω)3
= 23 + (-2ω)3
= 8 – 8ω3
= 8 – 8(1)
= 0
(v) (1 + ω)(1 + ω2)(1 + ω4)(1 + ω8)
Solution:
ω is the complex cube root of unity.
ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
(1 + ω)(1 + ω2)(1 + ω4)(1 + ω8)
= (1 + ω)(1 + ω2)(1 + ω)(1 + ω2) …..[∵ ω3 = 1, ω4 = ω]
= (-ω2)(-ω)(-ω2)(-ω)
= ω6
= (ω3)2
= (1)2
= 1
![]()
Question 4.
If α and β are the complex cube roots of unity, show that
(i) α2 + β2 + αβ = 0
(ii) α4 + β4 + α-1β-1 = 0
Solution:
α and β are the complex cube roots of unity.


Question 5.
If x = a + b, y = αa + βb and z = aβ + bα, where α and β are complex cube roots of unity, show that xyz = a3 + b3.
Solution:
x = a + b, y = αa + βb, z = aβ + bα
α and β are the complex cube roots of unity.
∴ α = \(\frac{-1+i \sqrt{3}}{2}\) and β = \(\frac{-1-i \sqrt{3}}{2}\)

![]()
Question 6.
Find the equation in cartesian coordinates of the locus of z if
(i) |z| = 10
Solution:
Let z = x + iy
|z| = 10
|x + iy| = 10
\(\sqrt{x^{2}+y^{2}}\) = 10
∴ x2 + y2 = 100
(ii) |z – 3| = 2
Solution:
Let z = x + iy
|z – 3| = 2
|x + iy – 3| = 2
|(x – 3) + iy| = 2
\(\sqrt{(x-3)^{2}+y^{2}}\) = 2
∴ (x – 3)2 + y2 = 4
(iii) |z – 5 + 6i| = 5
Solution:
Let z = x + iy
|z – 5 + 6i| = 5
|x + iy – 5 + 6i| = 5
|(x – 5) + i(y + 6)| = 5
\(\sqrt{(x-5)^{2}+(y+6)^{2}}\) = 5
∴ (x – 5)2 + (y + 6)2 = 25
(iv) |z + 8| = |z – 4|
Solution:
Let z = x + iy
|z + 8| = |z – 4|
|x + iy + 8| = |x + iy – 4|
|(x + 8) + iy | = |(x – 4) + iy|
\(\sqrt{(x+8)^{2}+y^{2}}=\sqrt{(x-4)^{2}+y^{2}}\)
(x + 8)2 + y2 = (x – 4)2 + y2
x2 + 16x + 64 + y2 = x2 – 8x + 16 + y2
16x + 64 = -8x + 16
24x + 48 = 0
∴ x + 2 = 0
![]()
(v) |z – 2 – 2i | = |z + 2 + 2i|
Solution:
Let z = x + iy
|z – 2 – 2i| = |z + 2 + 2i|
|x + iy – 2 – 2i | = |x + iy + 2 + 2i |
|(x – 2) + i(y – 2)| = |(x + 2) + i(y + 2)|
\(\sqrt{(x-2)^{2}+(y-2)^{2}}=\sqrt{(x+2)^{2}+(y+2)^{2}}\)
(x – 2)2 + (y – 2)2 = (x + 2)2 + (y + 2)2
x2– 4x + 4 + y2 – 4y + 4 = x2 + 4x + 4 + y2 + 4y + 4
-4x – 4y = 4x + 4y
8x + 8y = 0
x + y = 0
y = -x
(vi) \(\frac{|z+3 i|}{|z-6 i|}=1\)
Solution:
Let z = x + iy
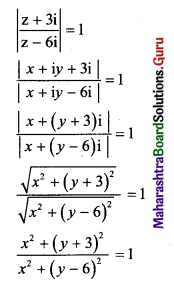
x2 + (y + 3)2 = x2 + (y – 6)2
y2 + 6y + 9 = y2 – 12y + 36
18y – 27 = 0
2y – 3 = 0
Question 7.
Use De Moivre’s theorem and simplify the following:
(i) \(\frac{(\cos 2 \theta+i \sin 2 \theta)^{7}}{(\cos 4 \theta+i \sin 4 \theta)^{3}}\)
Solution:


(ii) \(\frac{\cos 5 \theta+i \sin 5 \theta}{(\cos 3 \theta-i \sin 3 \theta)^{2}}\)
Solution:

(iii) \(\frac{\left(\cos \frac{7 \pi}{13}+i \sin \frac{7 \pi}{13}\right)^{4}}{\left(\cos \frac{4 \pi}{13}-i \sin \frac{4 \pi}{13}\right)^{6}}\)
Solution:
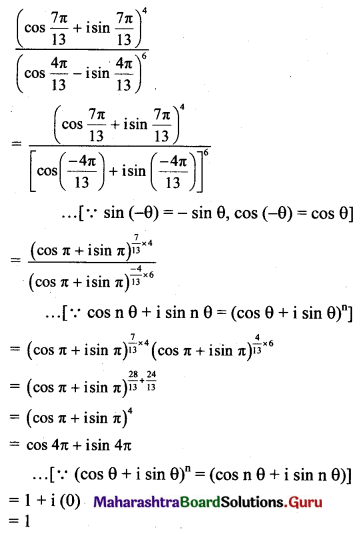
![]()
Question 8.
Express the following in the form a + ib, a, b ∈ R, using De Moivre’s theorem.
(i) (1 – i)5
Solution:


(ii) (1 + i)6
Solution:

(iii) (1 – √3 i)4
Solution:


![]()
(iv) (-2√3 – 2i)5
Solution: