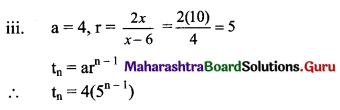Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 2 Sequences and Series Ex 2.1 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 2 Sequences and Series Ex 2.1
Question 1.
Check whether the following sequences are G.P. If so, write tn.
(i) 2, 6, 18, 54, ……
Solution:

(ii) 1, -5, 25, -125, ………
Solution:

(iii) \(\sqrt{5}, \frac{1}{\sqrt{5}}, \frac{1}{5 \sqrt{5}}, \frac{1}{25 \sqrt{5}}, \cdots\)
Solution:

![]()
(iv) 3, 4, 5, 6, ……
Solution:

(v) 7, 14, 21, 28, ……
Solution:

Question 2.
For the G.P.
(i) If r = \(\frac{1}{3}\), a = 9, find t7.
Solution:

(ii) If a = \(\frac{7}{243}\), r = 3, find t6.
Solution:

(iii) If r = -3 and t6 = 1701, find a.
Solution:

(iv) If a = \(\frac{2}{3}\), t6 = 162, find r.
Solution:
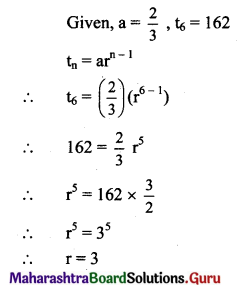
![]()
Question 3.
Which term of the G. P. 5, 25, 125, 625, …… is 510?
Solution:

Question 4.
For what values of x, the terms \(\frac{4}{3}\), x, \(\frac{4}{27}\) are in G. P.?
Solution:

Question 5.
If for a sequence, \(\mathrm{t}_{\mathrm{n}}=\frac{5^{n-3}}{2^{n-3}}\), show that the sequence is a G. P. Find its first term and the common ratio.
Solution:

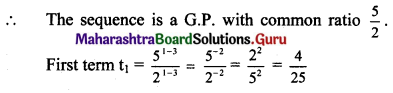
Question 6.
Find three numbers in G. P. such that their sum is 21 and the sum of their squares is 189.
Solution:
Let the three numbers in G. P. be \(\frac{a}{r}\), a, ar.
According to the given conditions,


When a = 6, r = 2,
\(\frac{a}{r}\) = 3, a = 6, ar = 12
Hence, the three numbers in G.P. are 12, 6, 3 or 3, 6, 12.
![]()
Check:
If sum of the three numbers is 21 and sum of their squares is 189, then our answer is correct.
Sum of the numbers = 12 + 6 + 3 = 21
Sum of the squares of the numbers = 122 + 62 + 32
= 144 + 36 + 9
= 189
Thus, our answer is correct.
Question 7.
Find four numbers in G. P. such that the sum of the middle two numbers is \(\frac{10}{3}\) and their product is 1.
Solution:
Let the four numbers in G.P. be \(\frac{a}{r^{3}}, \frac{a}{r}, a r, a r^{3}\)
According to the given conditions,


Question 8.
Find five numbers in G. P. such that their product is 1024 and the fifth term is square of the third term.
Solution:
Let the five numbers in G. P. be
\(\frac{a}{r^{2}}, \frac{a}{r}, a, a r, a r^{2}\)
According to the given conditions,

Hence, the five numbers in G.P. are
1, 2, 4, 8, 16 or 1, -2, 4, -8, 16.
Question 9.
The fifth term of a G. P. is x, the eighth term of a G.P. is y and the eleventh term of a G.P. is z, verify whether y2 = xz.
Solution:

Question 10.
If p, q, r, s are in G.P., show that p + q, q + r, r + s are also in G. P.
Solution:
p, q, r, s are in G.P.
∴ \(\frac{\mathrm{q}}{\mathrm{p}}=\frac{\mathrm{r}}{\mathrm{q}}=\frac{\mathrm{s}}{\mathrm{r}}\)
Let \(\frac{\mathrm{q}}{\mathrm{p}}=\frac{\mathrm{r}}{\mathrm{q}}=\frac{\mathrm{s}}{\mathrm{r}}\) = k
∴ q = pk, r = qk, s = rk
We have to prove that p + q, q + r, r + s are in G.P.
i.e., to prove that \(\frac{\mathrm{q}+\mathrm{r}}{\mathrm{p}+\mathrm{q}}=\frac{\mathrm{r}+\mathrm{s}}{\mathrm{q}+\mathrm{r}}\)

∴ p + q, q + r, r + s are in G.P.
![]()
Question 11.
The number of bacteria in a culture doubles every hour. If there were 50 bacteria originally in the culture, how many bacteria will be there at the end of the 5th hour?
Solution:
Since the number of bacteria in culture doubles every hour, increase in number of bacteria after every hour is in G.P.
∴ a = 50, r = \(\frac{100}{50}\) = 2
tn = arn-1
To find the number of bacteria at the end of the 5th hour.
(i.e., to find the number of bacteria at the beginning of the 6th hour, i.e., to find t6.)
∴ t6 = ar5
= 50 × (25)
= 50 × 32
= 1600
Question 12.
A ball is dropped from a height of 80 ft. The ball is such that it rebounds \(\left(\frac{3}{4}\right)^{\text {th }}\) of the height it has fallen. How high does the ball rebound on the 6th bounce? How high does the ball rebound on the nth bounce?
Solution:
Since the ball rebounds \(\left(\frac{3}{4}\right)^{\text {th }}\) of the height it has fallen, the height in successive bounce is in G.P.
1st height in the bounce = 80 × \(\frac{3}{4}\)
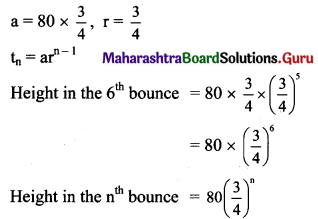
Question 13.
The numbers 3, x and x + 6 are in G. P. Find
(i) x
(ii) 20th term
(iii) nth term.
Solution:
(i) 3, x and x + 6 are in G. P.
\(\frac{x}{3}=\frac{x+6}{x}\)
x2 = 3x + 18
x2 – 3x – 18 = 0
(x – 6) (x + 3) = 0
x = 6, -3
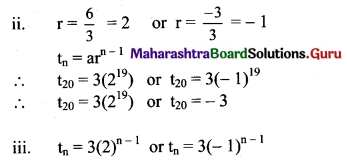
![]()
Question 14.
Mosquitoes are growing at a rate of 10% a year. If there were 200 mosquitoes in the beginning, write down the number of mosquitoes after
(i) 3 years
(ii) 10 years
(iii) n years
Solution:
a = 200, r = 1 + \(\frac{10}{100}\) = \(\frac{11}{10}\)
Mosquitoes at the end of 1st year = 200 × \(\frac{11}{10}\)
(i) Number of mosquitoes after 3 years
= 200 × \(\frac{11}{10} \times\left(\frac{11}{10}\right)^{2}\)
= 200 \(\left(\frac{11}{10}\right)^{3}\)
= 200 (1.1)3
(ii) Number of mosquitoes after 10 years = 200 (1.1)10
(iii) Number of mosquitoes after n years = 200 (1.1)n
Question 15.
The numbers x – 6, 2x and x2 are in G. P. Find
(i) x
(ii) 1st term
(iii) nth term
Solution:
(i) x – 6, 2x and x are in Geometric progression.
∴ \(\frac{2 x}{x-6}=\frac{x^{2}}{2 x}\)
4x2 = x2(x – 6)
4 = x – 6
x = 10
![]()
(ii) t1 = x – 6 = 10 – 6 = 4