Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 2 Trigonometry – I Ex 2.2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 2 Trigonometry – I Ex 2.2
Question 1.
If 2sin A = 1 = \(\sqrt{2}\) cos B and \(\frac{\pi}{2}\) < A < π, \(\frac{3 \pi}{2}\)
Solution:
Given, 2sin A = 1
∴ sin A = 1/2
we know that,
cos2 A = 1 – sin2 A = 1 – \(\left(\frac{1}{2}\right)^{2}=1-\frac{1}{4}=\frac{3}{4}\)
∴ cos A = \(\pm \frac{\sqrt{3}}{2}\)
Since \(\frac{\pi}{2}\) < A < π
A lies in the 2nd quadrant.

We know that,
Sin2 B = 1 – cos2 B = 1 – \(\left(\frac{1}{\sqrt{2}}\right)^{2}\)\(\frac{1}{2}=\frac{1}{2}\)
∴ sin B = \(\pm \frac{1}{\sqrt{2}}\)
Since \(\frac{3 \pi}{2}\) < B < 2π
B lies in the 4th quadrant,

![]()
Question 2.
If \(\) and A, B are angles in the second quadran, then prove that 4cosA + 3 cos B = -5
Solution:
Given, \(\frac{\sin \mathrm{A}}{3}=\frac{\sin \mathrm{B}}{4}=\frac{1}{5}\)
∴ sin A = \(\frac{3}{5}\) and sin B = \(\frac{4}{5}\)
We know that,
cos2 A = 1 – sin2 = 1 – \(\left(\frac{3}{5}\right)^{2}\) = 1 – \(\frac{9}{25}=\frac{16}{25}\)
∴ Cos A = ± \([{4}{5}\)
Since A lies in the second quadrant,
cos A < 0
∴ Cos A = –\(\frac{4}{5}\)
Sin B = 4/5
We know that,
cos2B = 1 – sin2B = 1 – \(\left(\frac{4}{5}\right)^{2}=1-\frac{16}{25}=\frac{9}{25}\)
∴ Cos B = ±\(\frac{4}{5}\)
Since B lies in the second quadrant, cos B < 0

Question 3.
If tan θ = \(\frac{1}{2}\), evaluate \(\frac{2 \sin \theta+3 \cos \theta}{4 \cos \theta+3 \sin \theta}\)
Solution:

Question 4.
Eliminate 0 from the following:
i. x = 3sec θ, y = 4tan θ
ii. x = 6cosec θ,y = 8cot θ
iii. x = 4cos θ – 5sin θ, y = 4sin θ + 5cos θ
iv. x = 5 + 6 cosec θ,y = 3 + 8 cot θ
v. x = 3 – 4tan θ,3y = 5 + 3sec θ
Solution:
i. x = 3sec θ, y = 4tan θ
∴ sec θ = \(\frac{x}{3}\) and tan θ= \(\frac{y}{4}\)
We know that,
sec2θ – tan2θ = 1
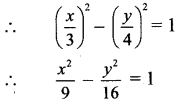
∴ 16x2 – 9y2 = 144
ii. x = 6cosec θ and y = 8cot θ
.’. cosec θ = \(\) and cot θ = \(\)
We know that,
cosec2 θ – cot2 θ =
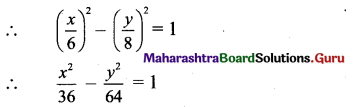
16x2 – 9y2 = 576
![]()
iii. x = 4cos θ – 5 sin θ … (i)
y = 4sin θ + 5cos θ .. .(ii)
Squaring (i) and (ii) and adding, we get
x2 + y2 = (4cos θ – 5sin θ)2 + (4sin θ + 5cos θ)2
= 16cos2θ – 40 sinθ cosθ + 25 sin2θ + 16 sin2 θ + 40sin θ cos θ + 25 cos2 θ
= 16(sin2 θ + cos2 θ) + 25(sin2 θ + cos2 θ)
= 16(1) + 25(1)
= 41
iv. x = 5 + 6cosec θ andy = 3 + 8cot θ
∴ x – 5 = 6cosec θ and y – 3 = 8cot θ
∴ cosec θ = \(\frac{x-5}{6}\) and cot θ = \(\frac{y-3}{8}\)
We know that,
cosec2 θ – cot2 θ = 1
∴ \(\left(\frac{x-5}{6}\right)^{2}-\left(\frac{y-3}{8}\right)^{2}\) = 1
v. 2x = 3 – 4tan θ and 3y = 5 + 3sec θ
∴ 2x – 3 = -4tan θ and 3y – 5 = 3sec θ
∴ tan θ = \(\frac{3-2 x}{4}\) and sec θ = \(\frac{3 y-5}{3}\)θ
We know that, sec2 θ – tan2 θ = 1
∴ \(\left(\frac{3 y-5}{3}\right)^{2}-\left(\frac{3-2 x}{4}\right)^{2}\) = 1
∴ \(\left(\frac{3 y-5}{3}\right)^{2}-\left(\frac{2 x-3}{4}\right)^{2}\) = 1
Question 5.
If 2sin2 θ + 3sin θ = 0, find the permissible values of cosθ.
Solution:
2sin2 θ + 3sin θ = 0
∴ sin θ (2sin θ + 3) = 0
∴ sin θ = 0 or sin θ = \(\frac{-3}{2}\)
Since – 1 ≤ sin θ ≤ 1,
sin θ = 0
\(\sqrt{1-\cos ^{2} \theta}\) = 0 …[ ∵ sin2 θ = 1- cos2 θ]
∴ 1 – cos2 θ = 0
∴ cos2 θ = 1
∴ cos θ = ±1 …[∵ – 1 ≤ cos θ ≤ 1]
Question 6.
If 2cos2 θ – 11 cos θ + 5 = 0, then find the possible values of cos θ.
Solution:
2cos2θ – 11 cos θ + 5 = 0
∴ 2cos2 θ – 10 cos θ – cos θ + 5 = 0
∴ 2cos θ(cos θ – 5) – 1 (cos θ – 5) = 0
∴ (cos θ – 5) (2cos θ – 1) = 0
cos θ – 5 = 0 or 2cos θ – 1 = 0
∴ cos θ = 5 or cos θ = 1/2
Since, -1 ≤ cos θ ≤ 1
∴ cos θ = 1/2
Question 7.
Find the acute angle θ such 2cos2 θ = 3sin θ.
Solution:
2cos20 = 3sin θ
∴ 2(1 – sin2 θ) = 3sin θ
∴ 2 – 2sin2 θ = 3sin θ
∴ 2sin2 θ + 3sin 9-2 = θ
∴ 2sin2 θ + 4sin θ – sin θ – 2 = θ
∴ 2sin θ(sin θ + 2) -1 (sin θ + 2) = θ
∴ (sin θ + 2) (2sin θ – 1) = 0
∴ sin θ + 2 = 0 or 2sin θ – 1 = 0
∴ sin θ = -2 or sin θ = 1/2
Since, -1 ≤ sin θ ≤ 1
∴ Sin θ = 1/2
∴ θ = 30° …[ ∵ sin 30 = 1/2]
![]()
Question 8.
Find the acute angle 0 such that 5tan2 0 + 3 = 9sec 0.
Solution:
5tan2 θ + 3 = 9sec θ
∴ 5(sec2 θ – 1) + 3 = 9sec θ
∴ 5sec2 θ – 5 + 3 = 9sec θ
∴ 5sec2 θ – 9sec θ – 2 = 0
∴ 5sec2 θ – 10 sec θ + sec θ – 2 = 0
∴ 5sec θ(sec θ – 2) + 1(sec θ – 2) = 0
∴ (sec θ – 2) (5sec θ + 1) = 0
∴ sec θ – 2 = 0 or 5sec θ + 1 = 0
∴ sec θ = 2 or sec θ = -1/5
Since sec θ ≥ 1 or sec θ ≤ -1,
sec θ = 2
∴ θ = 60° … [ ∵ sec 60° = 2]
Question 9.
Find sin θ such that 3cos θ + 4sin θ = 4.
Solution:
3cos θ + 4sin θ = 4
∴ 3cos θ = 4(1 – sin θ)
Squaring both the sides, we get .
9cos2θ = 16(1 – sin θ)2
∴ 9(1 – sin2 θ) = 16(1 + sin2 θ – 2sin θ)
∴ 9 – 9sin2 θ = 16 + 16sin2 θ – 32sin θ
∴ 25sin2 θ – 32sin θ + 7 = 0
∴ 25sin2 θ – 25sin θ – 7sin θ + 7 = 0
25sin θ (sin θ – 1) – 7 (sin θ – 1) = 0
∴ (sin θ – 1) (25sin θ – 7) = 0
∴ sin θ – 1 = 0 or 25 sin θ – 7 = 0
∴ sin θ = 1 or sin θ = \(\frac{7}{25}\)
Since, -1 ≤ sin θ ≤ 1
∴ sin θ = 1 or \(\frac{7}{25}\)
[Note: Answer given in the textbook is 1. However, as per our calculation it is 1 or \(\frac{7}{25}\).]
Question 10.
If cosec θ + cot θ = 5, then evaluate sec θ.
Solution:
cosec θ + cot θ = 5
∴ \(\frac{1}{\sin \theta}+\frac{\cos \theta}{\sin \theta}=5\)
∴ \(\frac{1+\cos \theta}{\sin \theta}=5\)
∴ 1 + cos θ = 5.sin θ
Squaring both the sides, we get
1 + 2 cos θ + cos2 θ = 25 sin2 θ
∴ cos2 θ + 2 cos θ + 1 = 25 (1 – cos2 θ)
∴ cos2 θ + 2 cos θ + 1 = 25 – 25 cos2 θ
∴ 26 cos2 θ + 2 cos θ – 24 = 0
∴ 26 cos2 θ + 26 cos θ – 24 cos θ – 24 = 0
∴ 26 cos θ (cos θ + 1) – 24 (cos θ + 1) = 0
∴ (cos θ + 1) (26 cos θ – 24) = 0
∴ cos θ + 1 = θ or 26 cos θ – 24 = 0
∴ cos θ = -1 or cos θ = \(\frac{24}{26}=\frac{12}{13}\)
When cos θ = -1, sin θ = 0
∴ cot θ and cosec x are not defined,
∴ cos θ ≠ -1
∴ cos θ = \(\frac{12}{13}\)
∴ sec θ = \(\frac{1}{\cos \theta}=\frac{13}{12}\)
[Note: Answer given in the textbook is -1 or \(\frac{13}{12}\).
However, as per our calculation it is only \(\frac{13}{12}\).]
Question 11.
If cot θ = \(\frac{3}{4}\) and π < θ < \(\frac{3 \pi}{2}\), then find the value of 4 cosec θ + 5 cos θ.
Solution:
We know that,
cosec2θ = 1 + cot2 θ = \(\left(\frac{3}{4}\right)^{2}\) = 1 + \(\frac{9}{16}\)
∴ cosec2 θ = \(\frac{25}{16}\)
∴ cosec θ = \(\pm \frac{5}{4}\)
Since π < θ < \(\frac{3 \pi}{2}\)
θ lies in the third quadrant.
∴ cosec θ < 0
∴ cosec θ = –\(\frac{5}{4}\)
cot θ = \(\frac{3}{4}\)
tan θ = \(\frac{1}{\cot \theta}=\frac{4}{3}\)
We know that,
sec2 θ = 1 + tan2 θ = 1 + \(\left(\frac{4}{3}\right)^{2}\)
= 1 + \(\frac{16}{9}=\frac{25}{9}\)
∴ sec θ = ±\(\frac{5}{3}\)
Since θ lies in the third quadrant,
sec θ < 0
∴ sec θ = –\(\frac{5}{3}\)
cos θ = \(\frac{1}{\sec \theta}=\frac{-3}{5}\)
∴ 4cosec θ + 5cos θ
= \(4\left(-\frac{5}{4}\right)+5\left(-\frac{3}{5}\right)\)
= -5 – 3 = -8
[Note: The question has been modified.]
![]()
Question 12.
Find the Cartesian co-ordinates of points whose polar co-ordinates are:
i. (3, 90°) ii. (1, 180°)
Solution:
i. (r, θ) = (3, 90°)
Using x = r cos θ and y = r sin θ, where (x, y) are the required cartesian co-ordinates, we get
x = 3cos 90° and y = 3sin 90°
∴ x = 3(0) = 0 and y = 3(1) = 3
∴ the required cartesian co-ordinates are (0, 3).
ii. (r, θ) = (1, 180°)
Using x = r cos θ and y = r sin θ, where (x, y) are the required cartesian co-ordinates, we get
x = 1(cos 180°) and y = 1(sin 180°)
∴ x = -1 and y = 0
∴ the required cartesian co-ordinates are (-1, 0).
Question 13.
Find the polar co-ordinates of points whose Cartesian co-ordinates are:
1. (5, 5) ii. (1, \(\sqrt{3}\))
ii. (-1, -1) iv. (-\(\sqrt{3}\), 1)
Solution:
i. (x, y) = (5, 5)
∴ r = \(\sqrt{x^{2}+y^{2}}\) = \(\sqrt{25+25}\)
\(=\sqrt{50}=5 \sqrt{2}\)
tan θ = \(\frac{y}{x}=\frac{5}{5}\) = 1
Since the given point lies in the 1st quadrant,
θ = 45° …[∵ tan 45° = 1]
∴ the required polar co-ordinates are (\(5 \sqrt{2}\), 45°).
ii. (x, y) = ( 1, \(\sqrt{3}\))
∴ r = \(\sqrt{x^{2}+y^{2}}=\sqrt{1+3}=\sqrt{4}=2\)
tan θ = \(\frac{y}{x}=\frac{\sqrt{3}}{1}=\sqrt{3}\)
Since the given point lies in the 1st quadrant,
θ = 60° …[∵ tan 60° = \(\sqrt{3}\)]
∴ the required polar co-ordinates are (2, 60°).
iii. (x, y) = (-1, -1)
∴ r = \(\sqrt{x^{2}+y^{2}}=\sqrt{1+1}=\sqrt{2}\)
tan θ = \(\frac{y}{x}=\frac{-1}{-1}=1\)
∴ tan θ = tan \(\frac{\pi}{4}\)
Since the given point lies in the 3rd quadrant,
tan θ = tan \(\left(\pi+\frac{\pi}{4}\right)\) …[∵ tan (n + x) = tanx]
∴ tan θ = tan \(\left(\frac{5 \pi}{4}\right)\)
∴ θ = \(\frac{5 \pi}{4}\) = 225°
∴ the required polar co-ordinates are (\(\sqrt{2}\), 225°).
iv. (x, y) = (-\(\sqrt{3}\) , 1)
∴ r = \(\sqrt{x^{2}+y^{2}}=\sqrt{3+1}=\sqrt{4}=2\)
tan θ = \(\frac{y}{x}=\frac{1}{-\sqrt{3}}\) = -tan \(\frac{\pi}{6}\)
Since the given point lies in the 2nd quadrant,
tan θ = tan \(\left(\pi-\frac{\pi}{6}\right)\) …[∵ tan (π – x) = – tanx]
∴ tan θ = tan \(\left(\frac{5 \pi}{6}\right)\)
∴ θ = \(\frac{5 \pi}{6}\) = 150°
∴ the required polar co-ordinates are (2, 150°)
Question 14.
Find the values of:
i. sin\(\frac{19 \pi^{e}}{3}\)
ii. cos 1140°
iii. cot \(\frac{25 \pi^{e}}{3}\)
Solution:
i. We know that sine function is periodic with period 2π.
sin \(\frac{19 \pi}{3}\) = sin \(\left(6 \pi+\frac{\pi}{3}\right)\) = sin \(\frac{\pi}{3}=\frac{\sqrt{3}}{2}\)
ii. We know that cosine function is periodic with period 2π.
cos 1140° = cos (3 × 360° + 60°)
= cos 60° = \(\frac {1}{2}\)
iii. We know that cotangent function is periodic with period π.
cot \(\frac{25 \pi}{3}\) = cot \(\left(8 \pi+\frac{\pi}{3}\right)\) = cot \(\frac{\pi}{3}\) = \(\frac{1}{\sqrt{3}}\)
dhana work.txt
Displaying dhana work.txt.