Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.1 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 3 Trigonometry – II Ex 3.1
Question 1.
Find the values of:
i. sin 150°
ü. cos 75°
iii. tan 105°
iv. cot 225°
Solution:
i. sin 15° = sin (45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°
\(\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right)-\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right)=\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
[Note: Answer given in the textbook is \(\frac{\sqrt{3}+1}{2 \sqrt{2}}\) However, as per our calculation it is \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
![]()
ii. cos 75° = cos (45° + 30°)
= cos 45° cos 30° – sin 45° sin 30°

iii. tan 105° = tan (60° +45°)

iv. cot 225°

Question 2.
Perove the following:
i. \(\cos \left(\frac{\pi}{2}-x\right) \cos \left(\frac{\pi}{2}-y\right) -\sin \left(\frac{\pi}{2}-x\right) \sin \left(\frac{\pi}{2}-y\right)=-\cos (x+y)\)
Solution:
L.H.S

= -(cos x cos y – sin x sin y)
= – cos (x+y)
= R.H.S
ii. \(\tan \left(\frac{\pi}{4}+\theta\right)=\frac{1+\tan \theta}{1-\tan \theta}\)
L.H.S =\(\tan \left(\frac{\pi}{4}+\theta\right)\)
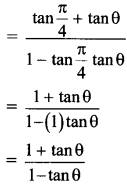
R.H.S.
[Note : The question has been modified.]
![]()
iii. \(\left(\frac{1+\tan x}{1-\tan x}\right)^{2}=\frac{\tan \left(\frac{\pi}{4}+x\right)}{\tan \left(\frac{\pi}{4}-x\right)}\)
Solution:
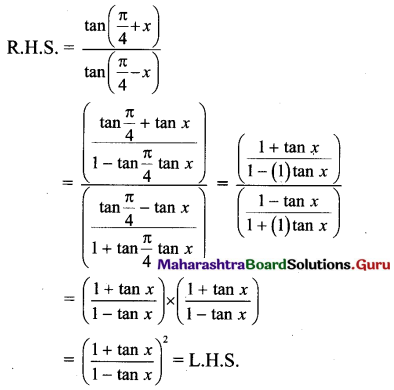
iv. sin [(n+1)A] . sin [(n+2)A] + cos [(n+1)A] . cos [(n+2)A] = cos A
Solution:
L.H.S. = sin [(n + 1)A] . sin [(n + 2)A] + cos [(n + 1)A] . cos [(n + 2)A]
= cos [(n + 2)A] . cos [(n + 1)A] + sin [(n + 2)A] . sin [(n + 1)A]
Let(n+2)Aaand(n+l)Ab …(i)
∴ L.H.S. = cos a. cos b + sin a. sin b
= cos (a — b)
= cos [(n + 2)A — (n + I )A]
…[From (i)]
cos[(n+2 – n – 1)A]
= cos A
= R.H.S.
v. \(\sqrt{2} \cos \left(\frac{\pi}{4}-\mathrm{A}\right)=\cos \mathrm{A}+\sin \mathrm{A}\)
Solution:

vi. \(\frac{\cos (x-y)}{\cos (x+y)}=\frac{\cot x \cot y+1}{\cot x \cot y-1}\)
Solution:

vii. cos (x + y). cos (x – y) = cos2y – sin2x
Solution:
L.H.S. = cos(x + y). cos(x – y)
= (cos x cos y – sin x sin y). (cos x cos y + sin x sin y)
= cos2 x cos2y – sin2x sin2y
…[∵ (a – b) (a + b) = a2 – b2]
= (1 – sin2x) cos2y – sin2x (1 – cos2y)
…[∵ sin2e + cos20 = 1]
= cos2y – cos2y sin2x – sin2x + sin2x cos2y
= cos2y – sin2x
=R.H.S.
![]()
viii.\(\frac{\tan 5 A-\tan 3 A}{\tan 5 A+\tan 3 A}=\frac{\sin 2 A}{\sin 8 A}\)
Solution:
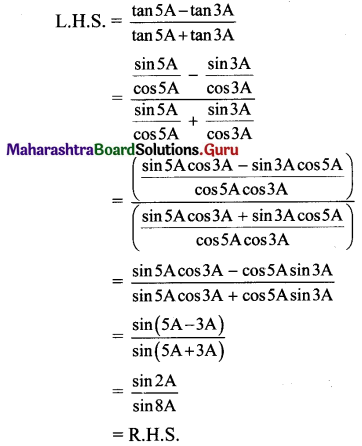
ix. tan 8θ – tan 5θ – tan 3θ = tan 8θ tan 5θ tan 3θ
Solution:
Since, 8θ = 5θ + 3θ
∴ tan 8θ = tan (5θ + 3θ)
∴ tan 8θ = \(\frac{\tan 5 \theta+\tan 3 \theta}{1-\tan 5 \theta \tan 3 \theta}\)
∴ tan 8θ (1 – tan 5θ.tan 3θ) = tan 5θ + tan 3θ
∴ tan 8θ – tan8θ.tan5θ.tan3θ = tan5θ + tan 3θ
∴ tan 8θ – tan 5θ – tan 3θ = tan 8θ.tan 5θ.tan 3θ
x. tan 50° = tan 40° + 2tan 10°
Solution:
Since, 50° = 10° +40°
∴ tan 50° = tan (10° + 40°)
∴ \(\frac{\tan 10^{\circ}+\tan 40^{\circ}}{1-\tan 10^{\circ} \tan 40^{\circ}}\)
∴ tan 50° (1 – tan 10° tan 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan 50° = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° tan (90° – 40°) = tan 10° + tan 40°
∴ tan 50° – tan 10° tan 40° cot 40°
= tan 10° + tan 40° …[∵ tan (90° – θ) = cot θ]
∴ tan 50° – tan 10° tan 40°. \(\frac{1}{\tan 40^{\circ}}\) = tan 10° + tan 40°
∴ tan 50° – tan 10°. 1 = tan 10° + tan 40°
∴ tan 50° = tan 40° + 2 tan 10°
xi. \(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}\) = tan 72°
Solution:
\(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}\)
Dividing numerator and cos 27°, we get denominator by cos 27°, we get
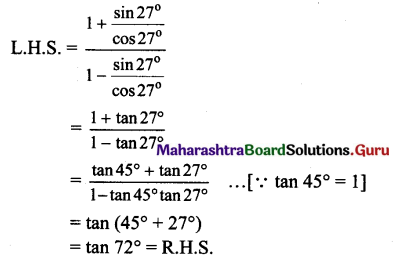
= tan (45° + 27°)
= tan 72° = R.H.S
xii. \(\frac{\cos 27^{\circ}+\sin 27^{\circ}}{\cos 27^{\circ}-\sin 27^{\circ}}=\tan 72^{\circ}\)
Solution:
Since 45° = 10° + 35°,
tan 45° = tan (10° +35°)
∴ \(\frac{\tan 10^{\circ}+\tan 35^{\circ}}{1-\tan 10^{\circ} \tan 35^{\circ}}\)
∴ 1 – tan 10° tan 35o = tan 10° + tan 35°
∴ tan 10° + tan 35° + tan 10° tan 35° = 1
xiii. tan 10° + tan 35° + tan 10°. tan 35° = 1
Solution:

![]()
xiv. \(\frac{\cos 15^{\circ}-\sin 15^{\circ}}{\cos 15^{\circ}+\sin 15^{\circ}}=\frac{1}{\sqrt{3}}\)
Solution:
Dividing numerator and cos 15°, we get

= tan (45° + 15°)
= tan 30° = \(\frac{1}{\sqrt{3}}\) = R.H.S
Question 3.
If sin A = \(-\frac{5}{13}\),π < A < \(\frac{3 \pi}{2}\) and cos B = \(\frac{3}{5}, \frac{3 \pi}{2}\) < B < 2π, find
i. sin (A+B)
ii. cos (A-B)
iii. tan (A + B)
Solution:
Given, sin A = \(-\frac{5}{13}\)
We know that,
cos2 A = 1 – sin2A = \(1-\left(-\frac{5}{13}\right)^{2}=1-\frac{25}{169}=\frac{144}{169}\)
∴ cos A = \(\pm \frac{12}{13}\)
Since, π < A < \(\frac{3 \pi}{2}\)
∴ ‘A’ lies in the 3rd quadrant.
∴ cos A<0
cos A = \(\frac{-12}{13}\)
Also,cos B = \(\frac{3}{5}\)
∴ sin2B = 1 – cos2B = \(1-\left(\frac{3}{5}\right)^{2}=1-\frac{9}{25}=\frac{16}{25}\)
∴ sin B = \(\pm \frac{4}{5}\)
Since, \(\frac{3 \pi}{2}\) < B < 2π
∴ ‘B’ lies in the 4th quadrant.
∴ sin B<0
Sin B = \(\frac{-4}{5}\)
i. sin (A + B) = sin A cos B+cos A sin B
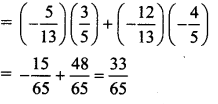
ii. cos (A -B) = cos A cos B + sin A sin B
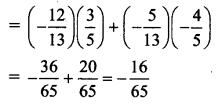
iii.
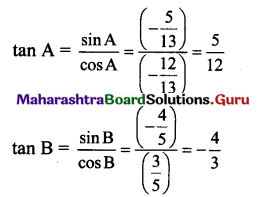
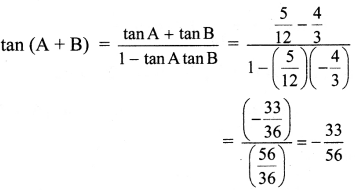
![]()
Question 4.
If tan A = \(\frac{5}{6}\) , tan B = \(\frac{1}{11}\) prove that A + B = \(\frac{\pi}{4}\)
Solution:
Given tan A = \(\frac{5}{6}\), tan B = \(\frac{1}{11}\)
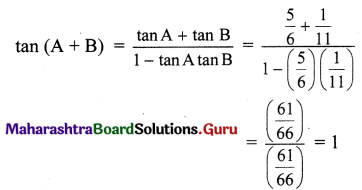
∴ tan (A + B) = tan \(\frac{\pi}{4}\)
∴ A + B = \(\frac{\pi}{4}\)