Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 3 Trigonometry – II Ex 3.2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 3 Trigonometry – II Ex 3.2
Question 1.
Find the values of:
i. sin 690°
ii. sin 495°
iii. cos 315°
iv. cos 600°
v. tan 225°
vi. tan (- 690°)
vii. sec 240°
viii. sec (- 855°)
ix. cosec 780°
x. cot (-1110°)
Solution:
i. sin 690° = sin (720° -30°)
Solution:
i. sin 690° = sin (720° -30°)
= sin (2 x 360° – 30°)
= – sin 30°
= \(\frac{-1}{2}\)
ii. sin 495° = sin (360° + 135°)
= sin (135°)
= sin (90° + 45°)
= cos 45°
= \(\frac{1}{\sqrt{2}}\)
![]()
iii. cos 315° = cos (270° + 45°)
sin 45° = \(\frac{1}{\sqrt{2}}\)
iv. cos 600° = cos (360° + 240°)
= cos 240°
= cos (180° + 60°)
= – cos 60°
= \(-\frac{1}{2}\)
v. tan 225° = tan (180° + 45°)
= tan 45°
= 1 .
vi. tan (- 690°) = – tan 690°
= – tan (720° – 30°)
= – tan (2 x 360° – 30°)
= – (- tan 30°)
= tan 30°
= \(\frac{1}{\sqrt{3}}\)
vii. sec 240° = sec (180° + 60°)
= – sec 60°
= – 2
viii. sec (-855°) = sec (855°)
= sec (720°+135°)
= sec (2 x360°+ 135°) = sec 135°
= sec (90° + 45°)
= – cosec 45°
= –\(\sqrt{2}\)
ix. cosec 780° = cosec (720° + 60°)
= cosec (2 x 360° + 60°)
= cosec 60°
= \(\frac{2}{\sqrt{3}}\)
x. cot (-1110°) =-cot (1110°)
= -cot (1080°+ 30°)
= – cot (3 x 360° + 30° )
= – cot 30°
= – \(\sqrt{3}\)
![]()
Question 2.
Prove the following:
i. \(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}=\cot ^{2} x\)
ii. \(\cos \left(\frac{3 \pi}{2}+x\right) \cos (2 \pi+x)\left[\cot \left(\frac{3 \pi}{2}-x\right)+\cot (2 \pi+x)\right]\)
iii. sec 840° cot (- 945°) + sin 600° tan (- 690°) = 3/2
iv. \(\frac{{cosec}\left(90^{\circ}-x\right) \sin \left(180^{\circ}-x\right) \cot \left(360^{\circ}-x\right)}{\sec \left(180^{\circ}+x\right) \tan \left(90^{\circ}+x\right) \sin (-x)}=1\)
v. \(\frac{\sin ^{3}(\pi+x) \sec ^{2}(\pi-x) \tan (2 \pi-x)}{\cos ^{2}\left(\frac{\pi}{2}+x\right) \sin (\pi-x) {cosec}^{2}(-x)}=\tan ^{3} x\)
vi. cos θ + sin (270° + θ) – sin (270° – θ) + cos (180° + θ) = 0
Solution:
i.

ii. L.H.S.
= cos ( \(\frac{3 \pi}{2}\) + x) cos (2π + x) . [cot ( – x) + (2π + x)]
= (sin x)(cos x) (tan x + cot x)
= sin x cos x ( \(\left(\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}\right)\))
= sin x cos x \(\left(\frac{\sin ^{2} x+\cos ^{2} x}{\sin x \cos x}\right)\)
= sin x cos x \(\left(\frac{1}{\sin x \cos x}\right)\)
= 1 = R.H.S
iii. sec 840° = sec (720° + 120°)
= sec (2 x 360° + 120°)
= sec (120°)
= sec (90° + 30°)
= – cosec 30°
= -2
cot(-945°) = -cot 945°
= -cot (720° + 225°)
= -cot (2 x 360° +225°)
= -cot (225°)
= -cot (180° + 459)
= -cot 45°
= -1
sin 600° = sin (360° + 240°)
= sin (240°)
= sin (180° +60°)
= – sin 60° = –\(\frac{\sqrt{3}}{2}\)
tan (-690°) = – tan 690°
= – tan (360° +330°)
= -tan (330°)
=- tan (360° – 30°)
=-(-tan 30°)
= tan 30°0 = \(\frac{1}{\sqrt{3}}\)
L.H.S. = sec 840° cot (-945°) + sin 600° tan (-690°)
= (-2)(-1) + \(\left(-\frac{\sqrt{3}}{2}\right)\left(\frac{1}{\sqrt{3}}\right)\)
= 2 – \(\frac{1}{2}=\frac{3}{2}\)
= R. H. S.
iv.
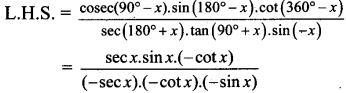
= 1
= R.H.S
![]()
v.
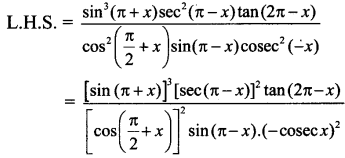
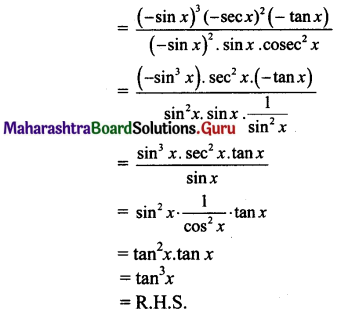
vi. L.H.S. = cos θ + sin (270° + θ) – sin (270° – θ) + cos (180° + θ)
= cos θ + (- cos θ)-(- cos θ) – cos θ
= cos θ – cos θ + cos θ – cos θ
= 0
= R.H.S.