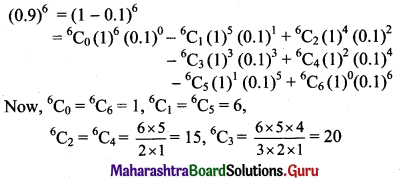Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Ex 4.2
Question 1.
Expand:
(i) (√3 + √2)4
Solution:
Here, a = √3, b = √2 and n = 4.
Using binomial theorem,

∴ (√3 + √2)4 = 1(9) (1) + 4(3√3) (√2) + 6(3)(2) + 4(√3) (2√2) + 1(1)(4)
= 9 + 12√6 + 36 + 8√6 + 4
= 49 + 20√6
(ii) (√5 – √2)5
Solution:
Here, a = √5, b = √2 and n = 5.
Using binomial theorem,

![]()
Question 2.
Expand:
(i) (2x2 + 3)4
Solution:
Here, a = 2x2, b = 3 and n = 4.
Using binomial theorem,
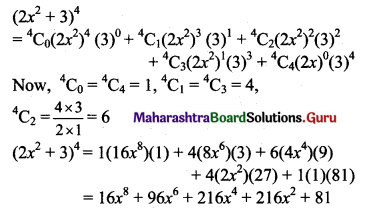
(ii) \(\left(2 x-\frac{1}{x}\right)^{6}\)
Solution:
Here, a = 2x, b = \(\frac{1}{x}\) and n = 6.
Using binomial theorem,
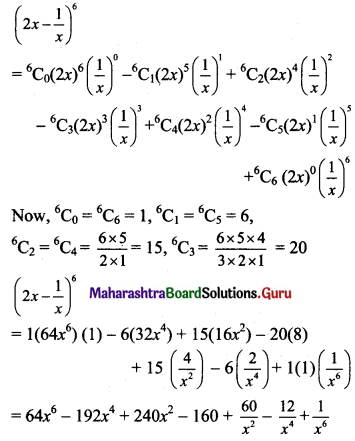
Question 3.
Find the value of
(i) (√3 + 1)4 – (√3 – 1)4
Solution:


(ii) (2 + √5)5 + (2 – √5)5
Solution:


Adding (i) and (ii), we get
∴ (2 + √5 )5 + (2 – √5)5 = (32 + 80√5 + 400 + 200√5 + 250 + 25√5) + (32 – 80√5 + 400 – 200√5+ 250 – 25√5 )
= 64 + 800 + 500
= 1364
![]()
Question 4.
Prove that:
(i) (√3 + √2)6 + (√3 – √2)6 = 970
Solution:



(ii) (√5 + 1)5 – (√5 – 1)5 = 352
Solution:


Question 5.
Using binomial theorem, find the value of
(i) (102)4
Solution:

(ii) (1.1)5
Solution:

![]()
Question 6.
Using binomial theorem, find the value of
(i) (9.9)3
Solution:

(ii) (0.9)4
Solution:

Question 7.
Without expanding, find the value of
(i) (x + 1)4 – 4(x + 1)3 (x – 1) + 6(x + 1)2 (x – 1)2 – 4(x + 1) (x – 1)3 + (x – 1)4
Solution:
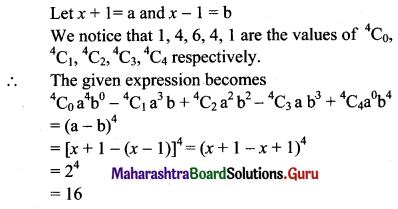
(ii) (2x – 1)4 + 4(2x – 1)3 (3 – 2x) + 6(2x – 1)2 (3 – 2x)2 + 4(2x – 1)1 (3 – 2x)3 + (3 – 2x)4
Solution:
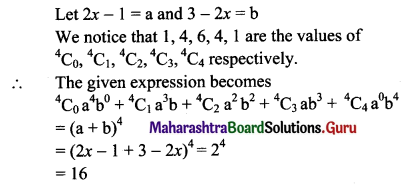
![]()
Question 8.
Find the value of (1.02)6, correct upto four places of decimals.
Solution:

Question 9.
Find the value of (1.01)5, correct upto three places of decimals.
Solution:

![]()
Question 10.
Find the value of (0.9)6, correct upto four places of decimals.
Solution: