Maharashtra Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Ex 4.3

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Ex 4.3

Question 1.
In the following expansions, find the indicated term.
(i) \(\left(2 x^{2}+\frac{3}{2 x}\right)^{8}\), 3rd term
Solution:

(ii) \(\left(x^{2}-\frac{4}{x^{3}}\right)^{11}\), 5th term
Solution:

(iii) \(\left(\frac{4 x}{5}-\frac{5}{2 x}\right)^{9}\), 7th term
Solution:

(iv) In \(\left(\frac{1}{3}+a^{2}\right)^{12}\), 9th term
Solution:

(v) In \(\left(3 a+\frac{4}{a}\right)^{13}\), 10th term
Solution:

Question 2.
In the following expansions, find the indicated coefficients.
(i) x³ in \(\left(x^{2}+\frac{3 \sqrt{2}}{x}\right)^{9}\)
Solution:

(ii) x⁸ in \(\left(2 x^{5}-\frac{5}{x^{3}}\right)^{8}\)
Solution:

(iii) x⁹ in \(\left(\frac{1}{x}+x^{2}\right)^{18}\)
Solution:

(iv) x^-3 in \(\left(x-\frac{1}{2 x}\right)^{5}\)
Solution:

(v) x^-20 in \(\left(x^{3}-\frac{1}{2 x^{2}}\right)^{15}\)
Solution:

Question 3.
Find the constant term (term independent of x) in the expansion of
(i) \(\left(2 x+\frac{1}{3 x^{2}}\right)^{9}\)
Solution:

(ii) \(\left(x-\frac{2}{x^{2}}\right)^{15}\)
Solution:

(iii) \(\left(\sqrt{x}-\frac{3}{x^{2}}\right)^{10}\)
Solution:

(iv) \(\left(x^{2}-\frac{1}{x}\right)^{9}\)
Solution:

(v) \(\left(2 x^{2}-\frac{5}{x}\right)^{9}\)
Solution:

Question 4.
Find the middle terms in the expansion of
(i) \(\left(\frac{x}{y}+\frac{y}{x}\right)^{12}\)
Solution:

(ii) \(\left(x^{2}+\frac{1}{x}\right)^{7}\)
Solution:

(iii) \(\left(x^{2}-\frac{2}{x}\right)^{8}\)
Solution:

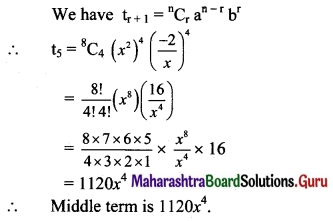
(iv) \(\left(\frac{x}{a}-\frac{a}{x}\right)^{10}\)
Solution:

(v) \(\left(x^{4}-\frac{1}{x^{3}}\right)^{11}\)
Solution:

Question 5.
In the expansion of (k + x)⁸, the coefficient of x⁵ is 10 times the coefficient of x⁶. Find the value of k.
Solution:

Question 6.
Find the term containing x⁶ in the expansion of (2 – x) (3x + 1)⁹.
Solution:

Question 7.
The coefficient of x² in the expansion of (1 + 2x)^m is 112. Find m.
Solution:
The coefficient of x² in (1 + 2x)^m = ^mC₂ (2²)
Given that the coefficient of x² = 112
∴ ^mC₂ (4) = 112
∴ ^mC₂ = 28
∴ \(\frac{\mathrm{m} !}{2 !(\mathrm{m}-2) !}=28\)
∴ \(\frac{m(m-1)(m-2) !}{2 \times(m-2) !}=28\)
∴ m(m – 1) = 56
∴ m² – m – 56 = 0
∴ (m – 8) (m + 7) = 0
As m cannot be negative.
∴ m = 8