Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Ex 4.5 Questions and Answers.
11th Maths Part 1 Determinants and Matrices Exercise 4.5 Questions And Answers Maharashtra Board
Question 1.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
5 & -4 \\
-6 & 1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
-1 & 2 \\
2 & 2 \\
0 & 3
\end{array}\right]\) and C = \(\left[\begin{array}{cc}
4 & 3 \\
-1 & 4 \\
-2 & 1
\end{array}\right]\)
Show that
i. A+B=B+A
ii. (A + B) + C = A + (B + C)
Solution:
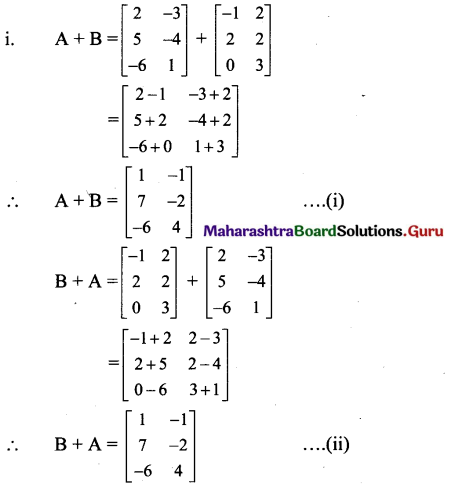
From (i) and (ii), we get
A + B = B + A
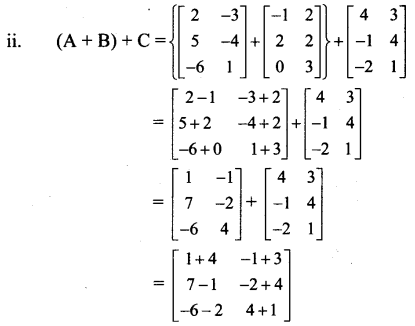

![]()
Question 2.
If A = \(\left[\begin{array}{cc}
1 & -2 \\
5 & 3
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & -3 \\
4 & -7
\end{array}\right]\) then find the matrix A – 2B + 6I, where I is the unit matrix of order 2.
Solution:
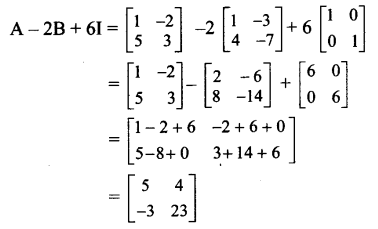
Question 3.
If A = \(\), B = \(\) then find the matrix C such that A + B + C is a zero matrix.
Solution:
A+ B + C is a zero matrix.
∴ A + B + C = O
C = -(A + B)
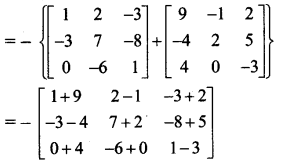
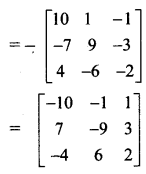
Question 4.
If A = \(\left[\begin{array}{cc}
1 & -2 \\
3 & -5 \\
-6 & 0
\end{array}\right]\) B = \(\left[\begin{array}{cc}
-1 & -2 \\
4 & 2 \\
1 & 5
\end{array}\right]\) and C = \(\left[\begin{array}{cc}
2 & 4 \\
-1 & -4 \\
-3 & 6
\end{array}\right]\) , find the matrix X such that 3A – 4B + 5X = C.
Solution:
3A-4B + 5X = C
∴ 5X = C + 4B – 3A

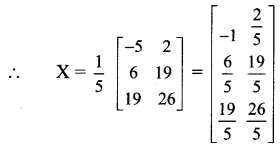
![]()
Question 5.
Solve the following equations for X and Y, if 3X – Y = \(=\left[\begin{array}{cc}
1 & -1 \\
-1 & 1
\end{array}\right]\) and X – 3Y = \(\left[\begin{array}{ll}
0 & -1 \\
0 & -1
\end{array}\right]\)
Solution:
Given equations are
\(=\left[\begin{array}{cc}
1 & -1 \\
-1 & 1
\end{array}\right]\)……………….. (i)
and X – 3Y = \(\left[\begin{array}{ll}
0 & -1 \\
0 & -1
\end{array}\right]\) ………………(ii)
By (i) x 3 – (ii) we get

Question 6.
Find the matrices A and B, if 2A – B = \(=\left[\begin{array}{ccc}
6 & -6 & 0 \\
-4 & 2 & 1
\end{array}\right]\) and A – 2B = \(\left[\begin{array}{ccc}
3 & 2 & 8 \\
-2 & 1 & -7
\end{array}\right]\)
Solution:
Given equations are
2A – B = \(=\left[\begin{array}{ccc}
6 & -6 & 0 \\
-4 & 2 & 1
\end{array}\right]\) ……………….. (i)
and A – 2B = \(\left[\begin{array}{ccc}
3 & 2 & 8 \\
-2 & 1 & -7
\end{array}\right]\) ……………….(ii)
By (i) – (ii) x 2, we get

![]()
Question 7.
Simplify \(\cos \theta\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]+\sin \theta\left[\begin{array}{cc}
\sin \theta & -\cos \theta \\
\cos \theta & \sin \theta
\end{array}\right]\)
Solution:
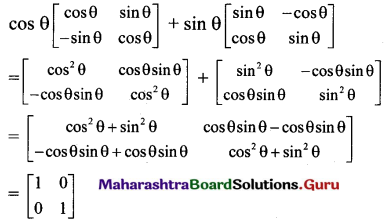
Quesiton 8.
If A = \(\left[\begin{array}{cc}
1 & 2 i \\
-3 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
2 i & 1 \\
2 & -3
\end{array}\right]\) where i =\(\sqrt{-1}\), find A + B and A – B. Show that A + B is singular. Is A – B singular? Justify your answer.
Solution:

Question 9.
Find x and y, if \(\left[\begin{array}{ccc}
2 x+y & -1 & 1 \\
3 & 4 y & 4
\end{array}\right]+\left[\begin{array}{ccc}
-1 & 6 & 4 \\
3 & 0 & 3
\end{array}\right]=\left[\begin{array}{ccc}
3 & 5 & 5 \\
6 & 18 & 7
\end{array}\right]\)
Solution:
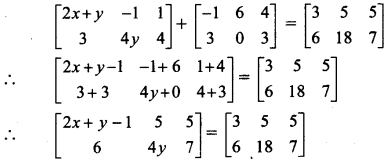
∴ By equality of matrices, we get
2x + y – 1 = 3 and 4y = 18
∴ 2x + y = 4 and y = \(\frac{18}{4}=\frac{9}{2}\)
∴ 2x + \(\frac{9}{2}\) = 4
∴ 2x = 4 – \(\frac{9}{2}\)
∴ 2x = \(\frac{1}{2}=\)
∴ x = –\(\frac{1}{4}=\) and y = \(\frac{9}{2}=\)
Question 10.
If \(\left[\begin{array}{ll}
2 a+b & 3 a-b \\
c+2 d & 2 c-d
\end{array}\right]=\left[\begin{array}{cc}
2 & 3 \\
4 & -1
\end{array}\right]\), find a, b, c and d.
Solution:
\(\left[\begin{array}{ll}
2 a+b & 3 a-b \\
c+2 d & 2 c-d
\end{array}\right]=\left[\begin{array}{cc}
2 & 3 \\
4 & -1
\end{array}\right]\)
∴ By equality of matrices, we get
2a + b = 2 ….(i)
3a – b = 3 ….(ii)
c + 2d = 4 ….(iii)
2c – d = -1 ….(iv)
Adding (i) and (ii), we get
5a = 5
∴ a = 1
Substituting a = 1 in (i), we get
2(1) + b = 2
∴ b = 0
By (iii) + (iv) x 2, we get
5c = 2
∴ c = \(\frac{2}{5}\)
Substituting c = \(\frac{2}{5}\) in (iii), we get
\(\frac{2}{5}\) + 2d = 4
∴ 2d = 4 – \(\frac{2}{5}\)
∴ 2d = \(\frac{18}{5}\)
∴ d = \(\frac{9}{5}\)
[Note: Answer given in the textbook is d = \(\frac{3}{5}\).
However, as per our calculation it is d = \(\frac{9}{5}\).]
![]()
Question 11.
There are two book shops owned by Suresh and Ganesh. Their sales (in Rupees) for books in three subjects – Physics, Chemistry and Mathematics for two months, July and August 2017 are given by two matrices A and B.
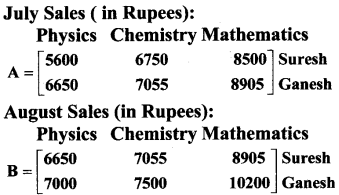
i. Find the increase in sales in Rupees from July to August 2017.
ii. If both book shops got 10% profit in the month of August 2017, find the profit for each bookseller in each subject in that month.
Solution:
i. Increase in sales in rupees from July to August 2017
For Suresh:
Increase in sales for Physics books
= 6650 – 5600= ₹ 1050
Increase in sales for Chemistry books
= 7055 – 6750 = ₹ 305
Increase in sales for Mathematics books
= 8905 – 8500 = ₹ 405
For Ganesh:
Increase in sales for Physics books
= 7000 – 6650 = ₹ 350
Increase in sales for Chemistry books
= 7500 – 7055 = ₹ 445
Increase in sales for Mathematics books
= 10200 – 8905 = ₹ 1295
[Note: Answers given in the textbook are 1760, 2090. However, as per our calculation, they are 1050, 305, 405, 350, 445, 1295.]
ii. Both book shops got 10% profit in the month of August 2017.
For Suresh:
Profit for Physics books = \(\frac{6650 \times 10}{100}\) = ₹ 665
Profit for Chemistry books = \(\frac{7055 \times 10}{100}\) = ₹ 705.50
Profit for Mathematics books = \(\frac{8905 \times 10}{100}\) = ₹ 890.50
For Ganesh:
Profit for Physics books = \(\frac{7000 \times 10}{100}\) = ₹ 700
Profit for Chemistry books = \(\frac{7500 \times 10}{100}\) = ₹ 750
Profit for Mathematics books = \(\frac{10200 \times 10}{100}\) = ₹ 1020
[Note: Answers given in the textbook for Suresh’s profit in Chemistry and Mathematics books are ? 675 and ?850 respectively. However, as per our calculation profit amounts are ₹ 705.50 and ₹ 890.50 respectively.]
11th Science Maths Chapter 4 Maths Solutions
- Determinants and Matrices Ex 4.1 Class 11 Maths Solutions
- Determinants and Matrices Ex 4.2 Class 11 Maths Solutions
- Determinants and Matrices Ex 4.3 Class 11 Maths Solutions
- Determinants and Matrices Miscellaneous Exercise 4(A) Class 11 Maths Solutions
- Determinants and Matrices Ex 4.4 Class 11 Maths Solutions
- Determinants and Matrices Ex 4.5 Class 11 Maths Solutions
- Determinants and Matrices Ex 4.6 Class 11 Maths Solutions
- Determinants and Matrices Ex 4.7 Class 11 Maths Solutions
- Determinants and Matrices Miscellaneous Exercise 4(B) Class 11 Maths Solutions