Maharashtra Board 11th Maths Solutions Chapter 4 Determinants and Matrices Ex 4.6

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Ex 4.6 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Determinants and Matrices Ex 4.6

Question 1.
Evaluate:
i. \(\left[\begin{array}{l}
3 \\
2 \\
1
\end{array}\right]\left[\begin{array}{lll}
{[2} & -4 & 3
\end{array}\right]\)
ii. \(\left[\begin{array}{lll}
2 & -1 & 3
\end{array}\right]\left[\begin{array}{l}
4 \\
3 \\
1
\end{array}\right]\)
Solution:
i. \(\begin{aligned}
\left[\begin{array}{l}
3 \\
2 \\
1
\end{array}\right]\left[\begin{array}{lll}
2 & -4 & 3
\end{array}\right] &=\left[\begin{array}{lll}
3(2) & 3(-4) & 3(3) \\
2(2) & 2(-4) & 2(3) \\
1(2) & 1(-4) & 1(3)
\end{array}\right] \\
&=\left[\begin{array}{ccc}
6 & -12 & 9 \\
4 & -8 & 6 \\
2 & -4 & 3
\end{array}\right]
\end{aligned}\)

ii. \(\left[\begin{array}{lll}
2 & -1 & 3
\end{array}\right]\left[\begin{array}{l}
4 \\
3 \\
1
\end{array}\right]\)
= [2(4)-1(3)+ 3(1)]
= [8 – 3 + 3] = [8]

Question 2.
If A = \(\left[\begin{array}{cc}
1 & -3 \\
4 & 2
\end{array}\right]\) B = \(\left[\begin{array}{cc}
4 & 1 \\
3 & -2
\end{array}\right]\), = show that AB ≠ BA.
Solution:

From (i) and (ii), we get
AB ≠ BA

Question 3.
If A = \(\left[\begin{array}{ccc}
-1 & 1 & 1 \\
2 & 3 & 0 \\
1 & -3 & 1
\end{array}\right]\) ,B = \(\left[\begin{array}{lll}
2 & 1 & 4 \\
3 & 0 & 2 \\
1 & 2 & 1
\end{array}\right]\) state whether AB = BA? Justify your answer.
Solution:


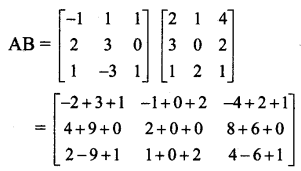
From (i) and (ii), we get
AB ≠ BA

Question 4.
Show that AB = BA, where
i. A = \(\left[\begin{array}{rrr}
-2 & 3 & -1 \\
-1 & 2 & -1 \\
-6 & 9 & -4
\end{array}\right]\) , B = \(\left[\begin{array}{rrr}
1 & 3 & -1 \\
2 & 2 & -1 \\
3 & 0 & -1
\end{array}\right]\)
ii. A = \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\), B = \(\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\)
Solution:

From (i) and (ii), we get
AB = BA

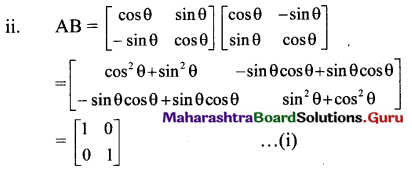
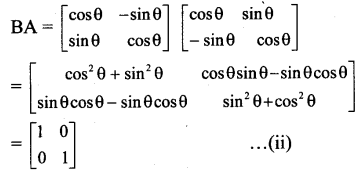
From (i) and (ii), we get
AB = BA
[Note: The question has been modified.]

Question 5.
If A = \(\left[\begin{array}{cc}
4 & 8 \\
-2 & -4
\end{array}\right]\), prove that A² = 0.
Solution:
A² = A.A
= \(\left[\begin{array}{cc}
4 & 8 \\
-2 & -4
\end{array}\right]\left[\begin{array}{cc}
4 & 8 \\
-2 & -4
\end{array}\right]\)
= \(\left[\begin{array}{cc}
16-16 & 32-32 \\
-8+8 & -16+16
\end{array}\right] \)
= \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\) = 0

Question 6.
Verify A(BC) = (AB)C in each of the following cases:
i. A = \(=\left[\begin{array}{cc}
4 & -2 \\
2 & 3
\end{array}\right]\), B = \(\left[\begin{array}{cc}
-1 & 1 \\
3 & -2
\end{array}\right]\) and C = \(\left[\begin{array}{cc}
4 & 1 \\
2 & -1
\end{array}\right]\)
ii. A = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 3 & 2
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 0 \\
-2 & 3 \\
4 & 3
\end{array}\right]\) and C = \(\left[\begin{array}{cc}
1 & 2 \\
-2 & 0 \\
4 & -3
\end{array}\right]\)
Solution:



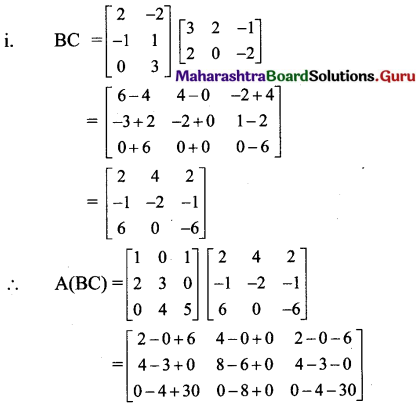
From (i) and (ii), we get
A(BC) = (AB)C.

Question 7.
Verify that A(B + C) = AB + AC in each of the following matrices:
i. A = \(\left[\begin{array}{cc}
4 & -2 \\
2 & 3
\end{array}\right]\), B = \(\left[\begin{array}{cc}
-1 & 1 \\
3 & -2
\end{array}\right]\) and C = \(=\left[\begin{array}{cc}
4 & 1 \\
2 & -1
\end{array}\right]\)
ii. A = \(\left[\begin{array}{ccc}
1 & -1 & 3 \\
2 & 3 & 2
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 0 \\
-2 & 3 \\
4 & 3
\end{array}\right]\) and C = \(\left[\begin{array}{cc}
1 & 2 \\
-2 & 0 \\
4 & -3
\end{array}\right]\)
Solution:

From (i) and (ii), we get
A(B + C) = AB + AC.
[Note: The question has been modified.]

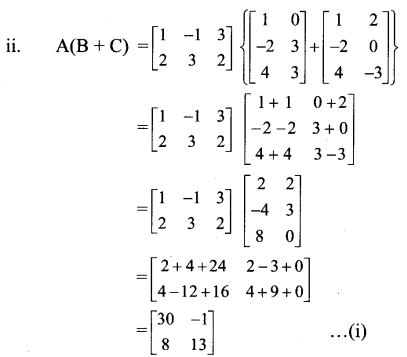
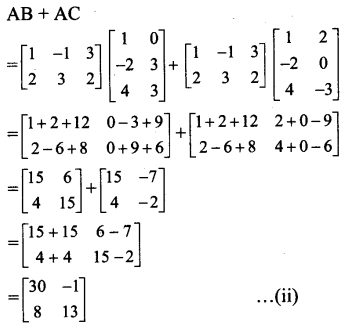
Question 8.
If A = \(\left[\begin{array}{cc}
1 & -2 \\
5 & 6
\end{array}\right]\), B = \(\left[\begin{array}{cc}
3 & -1 \\
3 & 7
\end{array}\right]\), find AB – 2I, where I is unit matrix of order 2.
Solution:

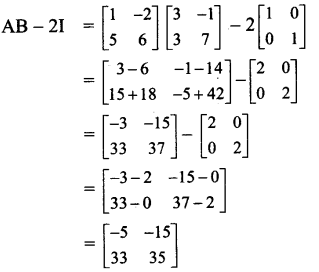
Question 9.
If A = \(\left[\begin{array}{ccc}
4 & 3 & 2 \\
-1 & 2 & 0
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 0 \\
1 & -2
\end{array}\right]\), show that matrix AB is non singular.
Solution:
im
∴ AB is non-singular matrix.

Question 10.
If A = \(\), find the product (A + I)(A – I).
Solution:

[Note : Answer given in the textbook is \(\left[\begin{array}{ccc}
9 & 6 & 4 \\
15 & 32 & -2 \\
35 & -7 & 29
\end{array}\right]\)
However, as per our calculation it is \(\left[\begin{array}{ccc}
10 & 10 & 4 \\
25 & 39 & 2 \\
35 & 7 & 22
\end{array}\right]\). ]

Question 11.
If A = \(\left[\begin{array}{ll}
\alpha & 0 \\
1 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & 0 \\
2 & 1
\end{array}\right]\), find α, if A² = B.
Solution:
A² = B

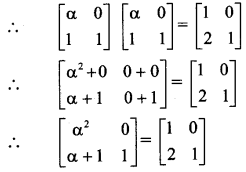
∴ By equality of matrices, we get
α² = 1 and α + 1 = 2
∴ α = ± 1 and α = 1
∴ α = 1

Question 12.
If A = \(\left[\begin{array}{lll}
1 & 2 & 2 \\
2 & 1 & 2 \\
2 & 2 & 1
\end{array}\right]\), show that A² – 4A is scalar matrix.
Solution:
A² – 4A = A.A – 4A

Question 13.
If A = \(\left[\begin{array}{cc}
1 & 0 \\
-1 & 7
\end{array}\right]\), find k so that A² – 8A – kI = O, where I is a unit matrix and O is a null matrix of order 2.
Solution:
A² – 8A – kI = O
∴ A.A – 8A – kI = O

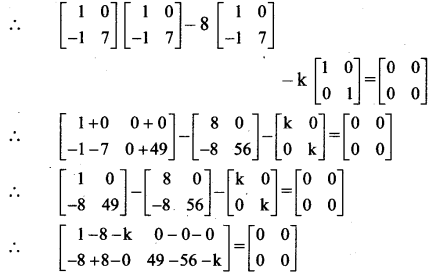
∴ by equality of matrices, we get
1 – 8 – k = 0
∴ k = -7

Question 14.
If A = \(\left[\begin{array}{cc}
8 & 4 \\
10 & 5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
5 & -4 \\
10 & -8
\end{array}\right]\), show that (A+B)² = A² + AB + B².
Solution:
We have to prove that (A + B)² = A² + AB + B²,
i.e., to prove A² + AB + BA + B² = A² + AB + B²,
i.e., to prove BA = 0.
BA = \(\left[\begin{array}{cc}
5 & -4 \\
10 & -8
\end{array}\right]\left[\begin{array}{cc}
8 & 4 \\
10 & 5
\end{array}\right]\)
\(\left[\begin{array}{cc}
40-40 & 20-20 \\
80-80 & 40-40
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)

Question 15.
If A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\), prove that A² – 5A + 7I = 0, where I is unit matrix of order 2.
Solution:
A² – 5A + 7I = 0 = A.A – 5A + 7I = 0

Question 16.
If A = \(\left[\begin{array}{cc}
3 & 4 \\
-4 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
2 & 1 \\
-1 & 2
\end{array}\right]\), show that (A + B)(A – B) = A² – B².
Solution:
We have to prove that (A + B)(A – B) = A² – B²,
i.e., to prove A² – AB + BA – B² = A² – B²,
i.e., to prove – AB + BA = 0,
i.e., to prove AB – BA.

From (i) and (ii), we get AB = BA

Question 17.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & -2
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & a \\
-1 & b
\end{array}\right]\) and (A + B)² = A² + B², find the values of a and b.
Solution:
Given, (A + B)² = A² + B²
∴ A² + AB + BA + B² = A² + B²
∴ AB + BA = 0
∴ AB = -BA

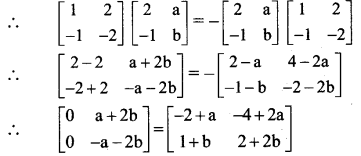
∴ by equality of matrices, we get
– 2 + a = 0 and 1 + b = 0
a = 2 and b = -1
[Note: The question has been modified.]

Question 18.
Find matrix X such that AX = B,
where A = \(\left[\begin{array}{cc}
1 & -2 \\
-2 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{c}
-3 \\
-1
\end{array}\right]\)
Solution:
Let X = \(\left[\begin{array}{c}
a \\
b
\end{array}\right]\)
But AX = B
∴ \(\left[\begin{array}{cc}
1 & -2 \\
-2 & 1
\end{array}\right]\left[\begin{array}{l}
\mathrm{a} \\
\mathrm{b}
\end{array}\right]=\left[\begin{array}{r}
-3 \\
-1
\end{array}\right]\)
∴ \(\left[\begin{array}{c}
a-2 b \\
-2 a+b
\end{array}\right]=\left[\begin{array}{l}
-3 \\
-1
\end{array}\right]\)
By equality of matrices, we get
a – 2b = -3 …(i)
-2a + b = -l …(ii)
By (i) x 2 + (ii), we get
-3b =-7
∴ b = \(\frac{7}{3}\)
Substituting b = \(\frac{7}{3}\) in (i), we get
a – 2 (\(\frac{7}{3}\)) = -3
∴ a = -3 + \(\frac{14}{3}=\frac{5}{3}\)
∴ X = \(\left[\begin{array}{l}
\frac{5}{3} \\
\frac{7}{3}
\end{array}\right]\)

Question 19.
Find k, if A = \(\left[\begin{array}{ll}
3 & -2 \\
4 & -2
\end{array}\right]\) and A² = KA – 2I
Solution:
A² = kA – 2I
∴ AA + 2I = kA

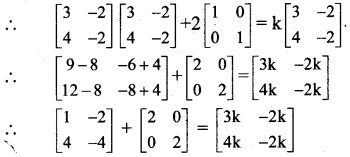
∴ \(\left[\begin{array}{ll}
3 & -2 \\
4 & -2
\end{array}\right]=\left[\begin{array}{ll}
3 k & -2 k \\
4 k & -2 k
\end{array}\right]\)
∴ By equality of matrices, we get
3k = 3
∴ k = 1

Question 20.
Find x, if \(\left[\begin{array}{lll}
1 & x & 1
\end{array}\right]\left[\begin{array}{ccc}
1 & 2 & 3 \\
4 & 5 & 6 \\
3 & 2 & 5
\end{array}\right]\left[\begin{array}{c}
1 \\
-2 \\
3
\end{array}\right]\) = 0
Solution:

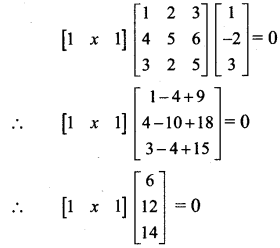
∴ [6 + 12x + 14] =[0]
∴ By equality of matrices, we get
∴ 12x + 20 = 0
∴ 12x =-20
∴ x = \(\frac{-5}{3}\)

Question 21.
Find x and y, if \(\left\{4\left[\begin{array}{ccc}
2 & -1 & 3 \\
1 & 0 & 2
\end{array}\right]-\left[\begin{array}{ccc}
3 & -3 & 4 \\
2 & 1 & 1
\end{array}\right]\right\}\left[\begin{array}{c}
2 \\
-1 \\
1
\end{array}\right]=\left[\begin{array}{l}
x \\
y
\end{array}\right]\)
Solution:

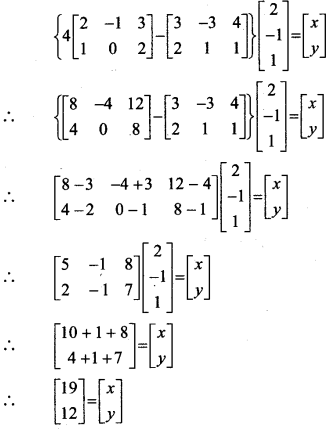
∴ By equality of matrices, we get
x = 19 andy = 12

Question 22.
Find x, y, z if
\(\left\{3\left[\begin{array}{ll}
2 & 0 \\
0 & 2 \\
2 & 2
\end{array}\right]-4\left[\begin{array}{cc}
1 & 1 \\
-1 & 2 \\
3 & 1
\end{array}\right]\right\}\left[\begin{array}{l}
1 \\
2
\end{array}\right]=\left[\begin{array}{c}
x-3 \\
y-1 \\
2 z
\end{array}\right]\)
Solution:

∴ By equality of matrices, we get
x – 3 = -6,y – 1 = 0, 2z = -2
∴ x = – 3, y = 1, z = – 1

Question 23.
If A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\) show that A² = \(=\left[\begin{array}{cc}
\cos 2 \alpha & \sin 2 \alpha \\
-\sin 2 \alpha & \cos 2 \alpha
\end{array}\right]\)
Solution:

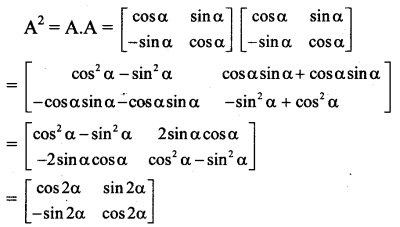
Question 24.
If A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
0 & 4 \\
2 & -1
\end{array}\right]\)
show that AB ≠ BA, but |AB| = |A| . |B|.
Solution:
AB = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 5
\end{array}\right]\left[\begin{array}{cc}
0 & 4 \\
2 & -1
\end{array}\right]\)

Now, |AB| = \(\left|\begin{array}{cc}
4 & 2 \\
10 & 7
\end{array}\right|\) = 28 – 20 = 8
|A| = \(\left|\begin{array}{ll}
1 & 2 \\
3 & 5
\end{array}\right|\) = 5 – 6 = -1
|B| = \(\left|\begin{array}{cc}
0 & 4 \\
2 & -1
\end{array}\right|\) = 0 – 8 = -8
∴ |A| . |B| = (-1).(-8) = 8 = |AB|
∴ AB ≠ BA, but |AB| = |A|.|B|

Question 25.
Jay and Ram are two friends in a class. Jay wanted to buy 4 pens and 8 notebooks, Ram wanted to buy 5 pens and 12 notebooks. Both of them went to a shop. The price of a pen and a notebook which they have selected was 6 and ₹ 10. Using matrix multiplication, find the amount required from each one of them.
Solution:
Let A be the matrix of pens and notebooks and B be the matrix of prices of one pen and one notebook.

The total amount required for each one of them is obtained by matrix AB.

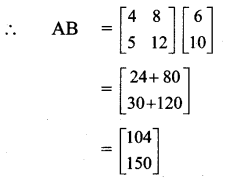
∴ Jay needs ₹ 104 and Ram needs ₹ 150.