Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 5 Sets and Relations Ex 5.1 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 5 Sets and Relations Ex 5.1
Question 1.
Describe the following sets in Roster form:
(i) A = {x/x is a letter of the word ‘MOVEMENT’}
(ii) B = {x/x is an integer, –\(\frac{3}{2}\) < x < \(\frac{9}{2}\)>
(iii) C = {x/x = 2n + 1, n ∈ N}
Solution:
(i) A = {M, O, V, E, N, T}
(ii) B = {-1, 0, 1, 2, 3, 4}
(iii) C = {3, 5, 7, 9, … }
![]()
Question 2.
Describe the following sets in Set-Builder form:
(i) {0}
(ii) {0, ±1, ±2, ±3}
(iii) \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
(iv) {0, -1, 2, -3, 4, -5, 6,…}
Solution:
(i) Let A = {0}
0 is a whole number but it is not a natural number.
∴ A = {x / x ∈ W, x ∉ N}
(ii) Let B = {0, ±1, ±2, ±3}
B is the set of elements which belongs to Z from -3 to 3.
∴ B = {x /x ∈ Z, -3 ≤ x ≤ 3}
(iii) Let C = \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
∴ C = {x / x = \(\frac{n}{n^{2}+1}\), n ∈ N, n ≤ 7}
(iv) Let D = {0, -1, 2, -3, 4, -5, 6, …}
∴ D = {x/x = (-1)n-1 × (n – 1), n ∈ N}
Question 3.
If A = {x / 6x2 + x – 15 = 0}, B = {x / 2x2 – 5x – 3 = 0}, C = {x / 2x2 – x – 3 = 0}, then find
(i) (A ∪ B ∪ C)
(ii) (A ∩ B ∩ C)
Solution:
A = [x/6x2 + x – 15 = 0)
6x2 + x – 15 = 0
6x2 + 10x – 9x – 15 = 0
2x(3x + 5) – 3(3x + 5) = 0
(3x + 5) (2x – 3) = 0
3x + 5 = 0 or 2x – 3 = 0
x = \(\frac{-5}{3}\) or x = \(\frac{3}{2}\)
A = {\(\frac{-5}{3}\), \(\frac{3}{2}\)}
B = {x/2x2 – 5x – 3 = 0}
2x2 – 5x – 3 = 0
2x2 – 6x + x – 3 = 0
2x(x – 3) + 1(x – 3) = 0
(x – 3)(2x + 1) = 0
x – 3 = 0 or 2x + 1 = 0
x = 3 or x = \(\frac{-1}{2}\)
B = (\(\frac{-1}{2}\), 3)
C = {x/2x2 – x – 3 = 0}
2x2 – x – 3 = 0
2x2 – 3x + 2x – 3 = 0
x(2x – 3) + 1(2x – 3) = 0
(2x – 3) (x + 1) = 0
2x – 3 = 0 or x + 1 = 0
x = \(\frac{3}{2}\) or x = -1
C = {-1, \(\frac{3}{2}\)}
(i) A ∪ B ∪ C = \(\left\{-\frac{5}{3}, \frac{3}{2}\right\} \cup\left\{\frac{-1}{2}, 3\right\} \cup\left\{-1, \frac{3}{2}\right\}\) = \(\left\{\frac{-5}{3},-1, \frac{-1}{2}, \frac{3}{2}, 3\right\}\)
(ii) A ∩ B ∩ C = { }
![]()
Question 4.
If A, B, C are the sets for the letters in the words ‘college’, ‘marriage’ and ‘luggage’ respectively, then verify that [A – (B ∪ C)] = [(A – B) ∩ (A – C)].
Solution:
A = {c, o, l, g, e}
B = {m, a, r, i, g, e}
C = {l, u, g, a, e}
B ∪ C = {m, a, r, i, g, e, l, u}
A – (B ∪ C) = {c, o}
A – B = {c, o, l}
A – C = {c, o}
∴ [(A – B) ∩ (A – C)] = {c, o} = A – (B ∪ C)
∴ [A -( B ∪ C)] = [(A – B) ∩ (A – C)]
Question 5.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8} and universal set X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then verify the following:
(i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(iii) (A ∪ B)’ = A’ ∩ B’
(iv) (A ∩ B)’ = A’ ∪ B’
(v) A = (A ∩ B) ∪ (A ∩ B’)
(vi) B = (A ∩ B) ∪ (A’ ∩ B)
(vii) (A ∪ B) = (A – B) ∪ (A ∩ B) ∪ (B – A)
(viii) A ∩ (B ∆ C) = (A ∩ B) ∆ (A ∩ C)
(ix) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
(x) n(B) = n (A’ ∩ B) + n (A ∩ B)
Solution:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8},
X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(i) B ∩ C = {4, 5, 6}
∴ A ∪ (B ∩ C) = {1, 2, 3, 4, 5, 6} …..(i)
A ∪ B = {1, 2, 3, 4, 5, 6}
A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
∴ (A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4, 5, 6} …….(ii)
From (i) and (ii), we get
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii) B ∪ C = {3, 4, 5, 6, 7, 8}
∴ A ∩ (B ∪ C) = {3, 4} ………(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) ∪ (A∩ C) = {3, 4} ……..(ii)
From (i) and (ii), we get
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(iii) A ∪ B = {1, 2, 3, 4, 5, 6}
∴ (A ∪ B)’ = {7, 8, 9, 10} ………(i)
A’ = {5, 6, 7, 8, 9, 10},
B’ = {1, 2, 7, 8, 9,10}
∴ A’ ∩ B’ = {7, 8, 9, 10} …….(ii)
From (i) and (ii), we get
(A ∪ B)’ = A’ ∩ B’
(iv) A ∩ B = {3, 4}
(A ∩ B)’= {1, 2, 5, 6, 7, 8, 9, 10} …….(i)
A’ = {5, 6, 7, 8, 9, 10}
B’ = {1, 2, 7, 8, 9, 10}
∴ A’ ∪ B’ = {1, 2, 5, 6, 7, 8, 9, 10} …….(ii)
From (i) and (ii), we get
(A ∩ B)’ = A’ ∪ B’
(v) A = {1, 2, 3, 4} ……(i)
A ∩ B = {3, 4}
B’ = {1, 2, 7, 8, 9, 10}
A ∩ B’ = {1, 2}
∴ (A ∩ B) ∪ (A ∩ B’) = {1, 2, 3, 4} …..(ii)
From (i) and (ii), we get
A = (A ∩ B) ∪ (A ∩ B’)
(vi) B = {3, 4, 5, 6} …..(i)
A ∩ B = {3, 4}
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ (A ∩ B) ∪ (A’ ∩ B) = {3, 4, 5, 6} …..(ii)
From (i) and (ii), we get
B = (A ∩ B) ∪ (A’ ∩ B)
(vii) A ∪ B = {1, 2, 3, 4, 5, 6} …….(i)
A – B = {1, 2}
A ∩ B = {3, 4}
B – A = {5, 6}
∴ (A – B) ∪ (A ∩ B) ∪ (B – A) = {1, 2, 3, 4, 5, 6} ……(ii)
From (i) and (ii), we get
A ∪ B = (A – B) ∪ (A ∩ B) ∪ (B – A)
![]()
(viii) B – C = {3}
C – B = {7, 8}
B Δ C = (B – C) ∪ (C – B) = {3, 7, 8}
∴ A ∩ (B Δ C) = {3} ……(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) Δ (A ∩ C) = [(A ∩ B) – (A ∩ C)] ∪ [(A ∩ C) – (A ∩ B)] = {3} …..(ii)
From (i) and (ii), we get
A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)
(ix) A = {1, 2, 3, 4}, B = {3, 4, 5, 6}
A ∩ B = {3, 4}, A ∪ B = {1, 2, 3, 4, 5, 6}
∴ n(A) = 4, n(B) = 4,
n(A ∩ B) = 2, n(A ∪ B) = 6 ……(i)
∴ n(A) + n(B) – n(A ∩ B) = 4 + 4 – 2
∴ n(A) + n(B) – n(A ∩ B) = 6 …..(ii)
From (i) and (ii), we get
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
(x) B = {3, 4, 5, 6}
∴ n(B) = 4 …..(i)
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ n(A’ ∩ B) = 2
A ∩ B = {3, 4}
∴ n(A ∩ B) = 2
∴ n(A’ ∩ B) + n(A ∩ B) = 2 + 2 = 4 …..(ii)
From (i) and (ii), we get
n(B) = n(A’ ∩ B) + n (A ∩ B)
Question 6.
If A and B are subsets of the universal set X and n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5, find
(i) n(A ∪ B)
(ii) n(A ∩ B)
(iii) n(A’ ∩ B)
(iv) n(A ∩ B’)
Solution:
n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5
(i) n(A ∪ B) = n(X) – [n(A ∪ B)’]
= n(X) – n(A’ ∩ B’)
= 50 – 5
= 45
(ii) n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 35 + 20 – 45
= 10
(iii) n(A’ ∩ B) = n(B) – n(A ∩ B)
= 20 – 10
= 10
(iv) n(A ∩ B’) = n(A) – n(A ∩ B)
= 35 – 10
= 25
![]()
Question 7.
In a class of 200 students who appeared in certain examinations, 35 students faded in CET, 40 in NEET and 40 in JEE, 20 faded in CET and NEET, 17 in NEET and JEE, 15 in CET and JEE and 5 faded in ad three examinations. Find how many students
(i) did not fail in any examination.
(ii) faded in NEET or JEE entrance.
Solution:
Let A = set of students who failed in CET
B = set of students who failed in NEET
C = set of students who failed in JEE
X = set of all students
∴ n(X) = 200, n(A) = 35, n(B) = 40, n(C) = 40, n(A ∩ B) = 20, n(B ∩ C) = 17, n(A ∩ C) = 15, n(A ∩ B ∩ C) = 5
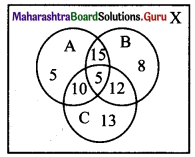
(i) n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
= 35 + 40 + 40 – 20 – 17 – 15 + 5
= 68
∴ No. of students who did not fail in any exam = n(X) – n(A ∪ B ∪ C)
= 200 – 68
= 132
(ii) No. of students who failed in NEET or JEE entrance = n(B ∪ C)
= n(B) + n(C) – n(B ∩ C)
= 40 + 40 – 17
= 63
Question 8.
From amongst 2000 Uterate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read
(i) at least one of the newspapers.
(ii) neither Marathi nor English newspaper.
(iii) only one of the newspapers.
Solution:
Let M = set of individuals who read Marathi newspapers
E = set of individuals who read English newspapers
X = set of all literate individuals
∴ n(X) = 2000,
n(M) = \(\frac{70}{100}\) × 2000 = 1400
n(E) = \(\frac{50}{100}\) × 2000 = 1000
n(M ∩ E) = \(\frac{32.5}{100}\) × 2000 = 650
(i) n(M ∪ E) = n(M) + n(E) – n(M ∩ E)
= 1400 + 1000 – 650
= 1750
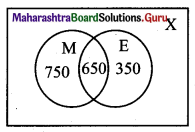
No. of individuals who read at least one of the newspapers = n(M ∪ E) = 1750.
(ii) No. of individuals who read neither Marathi nor English newspaper = n(M’ ∩ E’)
= n(M ∪ E)’
= n(X) – n(M ∪ E)
= 2000 – 1750
= 250
(iii) No. of individuals who read only one of the newspapers = n(M ∩ E’) + n(M’ ∩ E)
= n(M ∪ E) – n(M ∩ E)
= 1750 – 650
= 1100
![]()
Question 9.
In a hostel, 25 students take tea, 20 students take coffee, 15 students take milk, 10 students take both tea and coffee, 8 students take both milk and coffee. None of them take tea and milk both and everyone takes atleast one beverage, find the total number of students in the hostel.
Solution:
Let T = set of students who take tea
C = set of students who take coffee
M = set of students who take milk
∴ n(T) = 25, n(C) = 20, n(M) = 15, n(T ∩ C) = 10, n(M ∩ C) = 8, n(T ∩ M) = 0, n(T ∩ M ∩ C) = 0
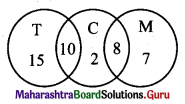
∴ Total number of students in the hostel = n(T ∪ C ∪ M)
= n(T) + n(C) + n(M) – n(T ∩ C) – n(M ∩ C) – n(T ∩ M) + n(T ∩ M ∩ C)
= 25 + 20 + 15 – 10 – 8 – 0 + 0
= 42
Question 10.
There are 260 persons with skin disorders. If 150 had been exposed to the chemical A, 74 to the chemical B, and 36 to both chemicals A and B, find the number of persons exposed to
(i) Chemical A but not Chemical B
(ii) Chemical B but not Chemical A
(iii) Chemical A or Chemical B
Solution:
Let A = set of persons exposed to chemical A
B = set of persons exposed to chemical B
X = set of all persons
∴ n(X) = 260, n(A) = 150, n(B) = 74, n(A ∩ B) = 36
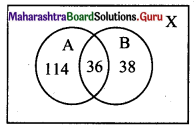
(i) No. of persons exposed to chemical A but not to chemical B = n(A ∩ B’)
= n(A) – n(A ∩ B)
= 150 – 36
= 114
(ii) No. of persons exposed to chemical B but not to chemical A = n(A’ ∩ B)
= n(B) – n(A ∩ B)
= 74 – 36
= 38
(iii) No. of persons exposed to chemical A or chemical B = n(A ∪ B)
= n(A) + n(B) – n(A ∩ B)
= 150 + 74 – 36
= 188
![]()
Question 11.
Write down the power set of A = {1, 2, 3}.
Solution:
A = {1, 2, 3}
The power set of A is given by
P(A) = {{Φ}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}}
Question 12.
Write the following intervals in Set-Builder form:
(i) (-3, 0)
(ii) [6, 12]
(iii) (6, ∞)
(iv) (-∞, 5]
(v) (2, 5]
(vi) [-3, 4)
Solution:
(i) (-3, 0) = {x / x ∈ R, -3 < x < 0}
(ii) [6, 12] = {x / x ∈ R, 6 ≤ x ≤ 12}
(iii) (6, ∞) = {x / x ∈ R, x > 6}
(iv) (-∞, 5] = {x / x ∈ R, x ≤ 5}
(v) (2, 5] = {x / x ∈ R, 2 < x ≤ 5}
(vi) [-3, 4) = {x / x ∈ R, -3 ≤ x < 4}
Question 13.
A college awarded 38 medals in volleyball, 15 in football, and 20 in basketball. The medals were awarded to a total of 58 players and only 3 players got medals in all three sports. How many received medals in exactly two of the three sports?
Solution:
Let A = Set of students who received medals in volleyball
B = Set of students who received medals in football
C = Set of students who received medals in basketball
n(A) = 38, n(B) = 15, n(C) = 20, n(A ∪ B ∪ C) = 58, n(A ∩ B ∩ C) = 3
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
58 = 38 + 15 + 20 – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + 3
∴ n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 ……(i)
Number of players who got exactly two medals = p + q + r
Here, s = n(A ∩ B ∩ C) = 3
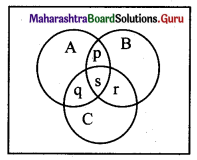
n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 …..[From (i)]
∴ p + s + s + r + q + s = 18
∴ p + q + r + 3s = 18
∴ p + q + r + 3(3) = 18
∴ p + q + r = 18 – 9 = 9
∴ Number of players who received exactly two medals = 9.
![]()
Question 14.
Solve the following inequalities and write the solution set using interval notation.
(i) -9 < 2x + 7 ≤ 19
(ii) x2 – x > 20
(iii) \(\frac{2 x}{x-4}\) ≤ 5
(iv) 6x2 + 1 ≤ 5x
Solution:
(i) -9 < 2x + 7 ≤ 19
∴ -16 < 2x ≤ 12
∴ -8< x ≤ 6
∴ x ∈ (-8, 6]
(ii) x2 – x > 20
∴ x2 – x – 20 > 0
∴ x2 – 5x + 4x – 20 > 0
∴ (x – 5) (x + 4) > 0
∴ either x – 5 > 0 and x + 4 > 0 or x – 5 < 0 and x + 4 < 0
Case I: x – 5 > 0 and x + 4 > 0
∴ x > 5 and x > -4
∴ x > 5 ….(i)
Case II:
x – 5 < 0 and x + 4 < 0
∴ x < 5 and x < -4
∴ x < -4 …..(ii)
From (i) and (ii), we get
x ∈ (-∞, – 4) ∪ (5, ∞)
(iii) \(\frac{2 x}{x-4}\) ≤ 5
∴ \(\frac{2 x}{x-4}\) – 5 ≤ 0
∴ \(\frac{2 x-5 x+20}{x-4}\) ≤ 0
∴ \(\frac{20-3 x}{x-4}\) ≤ 0
When \(\frac{a}{b}\) ≤ 0,
a ≥ 0 and b < 0 or a ≤ 0 and b > 0
∴ either 20 – 3x ≥ 0 and x – 4 < 0 or 20 – 3x ≤ 0 and x – 4 > 0
Case I:
20 – 3x ≥ 0 and x – 4 < 0
∴ x ≤ \(\frac{20}{3}\) and x < 4
∴ x < 4 ……(I)
Case II: 20 – 3x ≤ 0 and x – 4 > 0
∴ x ≥ \(\frac{20}{3}\) and x > 4
∴ x ≥ \(\frac{20}{3}\) ……(ii)
From (i) and (ii), we get
x ∈ (-∞, 4) ∪ [\(\frac{20}{3}\), ∞)
(iv) 6x2 + 1 ≤ 5x
6x2 – 5x + 1 ≤ 0
6x2 – 3x – 2x + 1 ≤ 0
(3x – 1) (2x – 1) ≤ 0
either 3x – 1 ≤ 0 and 2x – 1 ≥ 0 or 3x – 1 ≥ 0 and 2x – 1 ≤ 0
Case I:
3x – 1 ≤ 0 and 2x – 1 ≥ 0
∴ x ≤ \(\frac{1}{3}\) and x ≥ \(\frac{1}{2}\), which is not possible.
Case II:
3x – 1 ≥ 0 and 2x – 1 ≤ 0
∴ x ≥ \(\frac{1}{3}\) and x ≤ \(\frac{1}{2}\)
∴ x ∈ [\(\frac{1}{3}\), \(\frac{1}{2}\)]
![]()
Question 15.
If A = (-7, 3], B = [2, 6] and C = [4, 9], then find
(i) A ∪ B
(ii) B ∪ C
(iii) A ∪ C
(iv) A ∩ B
(v) B ∩ C
(vi) A ∩ C
(vii) A’ ∩ B
(viii) B’ ∩ C’
(ix) B – C
(x) A – B
Solution:
A = (-7, 3], B = [2, 6], C = [4, 9]
(i) A ∪ B = (-7, 6]
(ii) B ∪ C = [2, 9]
(iii) A ∪ C = (-7, 3] ∪ [4, 9]
(iv) A ∩ B = [2, 3]
(v) B ∩ C = [4, 6]
(vi) A ∩ C = { }
(vii) A’ = (-∞, – 7] ∪ (3, ∞)
∴ A’ ∩ B = (3, 6]
(viii) B’ = (-∞, 2) ∪ (6, ∞)
C’ = (-∞, 4) ∪ (9, ∞)
∴ B’ ∩ C’ = (-∞, 2) ∪ (9, ∞)
(ix) B – C = [2, 4)
(x) A – B = (-7, 2)