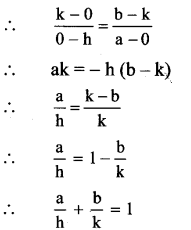Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 5 Straight Line Ex 5.2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 5 Straight Line Ex 5.2
Question 1.
Find the slope of each of the lines which passes through the following points:
i. A(2, -1), B(4,3)
ii. C(- 2,3), D(5, 7)
iii. E(2,3), F(2, – 1)
iv. G(7,1), H(- 3,1)
Solution:
i. Here, A = (2, -1) andB = (4, 3)
Slope of line AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-(-1)}{4-2}=\frac{4}{2}\) = 2
ii. Here, C = (-2, 3) and D = (5, 7)
Slope of line CD = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{7-3}{5-(-2)}=\frac{4}{7}\)
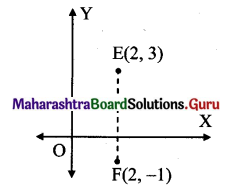
iii. Here, E s (2, 3) and F = (2, -1)
Slope of line EF = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-1-3}{2-2}=\frac{-4}{0}\), which ix not defined.
Alternate Method:
Points E and F have the same x co-ordinates i.e. 2.
Points E and F lie on a line parallel to Y-axis.
∴ The slope of EF is not defined.
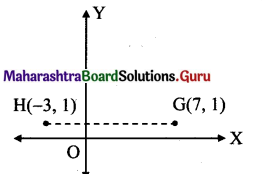
iv. Here, G = (7, 1) and H = (-3, 1)
Slope of line GH = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{1-1}{-3-7}\) = o
![]()
Alternate Method:
Points G and H have the same y co-ordinate i.e. 1.
∴ Points G and H lie on a line parallel to the
X-axis.
∴ The slope of GH is 0.
Question 2.
If the x and x-intercepts of line L are 2 and 3 respectively, then find the slope of line L.
Solution:
Given, the x-intercept of line L is 2 and the y-intercept of line L is 3
∴ The line L intersects X-axis at (2, 0) and Y-axis at (0,3).
∴ The line L passes through (2, 0) and (0, 3).
Slope of line L = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-0}{0-2}=\frac{-3}{2}\)
Question 3.
Find the slope of the line whose inclination is 30°.
Solution:
Given, inclination (θ) = 30°
∴ Slope of the line = tanθ = tan30° = \(\frac{1}{\sqrt{3}}\)
Question 4.
Find the slope of the line whose inclination is \(\frac{\pi}{4}\)
Solution:
Given, inclination (0) = \(\frac{\pi}{4}\)
∴ Slope of the line = tan θ = tan\(\frac{\pi}{4}\) = 1
Question 5.
A line makes intercepts 3 and 3 on the co-ordinate axes. Find the inclination of the line.
Solution:
Given, x-intercept of line is 3 and y-intercept of line is 3
∴ The line intersects X-axis at (3, 0) and Y-axis at (0, 3).
∴ The line passes through (3, 0) and (0,3).
∴ Slope of line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-0}{0-3}\) = -1
But, slope of a line = tan θ
∴ tan θ = – 1
= – tan \(\frac{\pi}{4}\)
= tan(π-\(\frac{\pi}{4}\) ) …[v tan(π – θ) = -tan θ]
tan θ = tan \(\frac{3\pi}{4}\)
θ = \(\frac{3\pi}{4}\)
The inclination of the line is \(\frac{3\pi}{4}\).
[Note: Answer given in the textbook is ‘-1 However, as per our calculation it is \(\frac{3\pi}{4}\)]
Question 6.
Without using Pythagoras theorem, show that points A (4, 4), B (3, 5) and C (- 1, – 1) are the vertices of a right-angled triangle.
Solution:
Given, A(4,4), B(3, 5), C (-1, -1).
Slope of AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{5-4}{3-4}\) = – 1
Slope of BC = \(\frac{-1-5}{-1-3}=\frac{-6}{-4}=\frac{3}{2}\)
Slope of AC = \(\frac{-1-4}{-1-4}\) = 1
Slope of AB x slope of AC = – 1 x 1 = – 1
∴ side AB ⊥ side AC
∴ ∆ABC is a right angled triangle right angled at A.
∴ The given points are the vertices of a right angled triangle.
![]()
Question 7.
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured anticlockwise.
Solution:
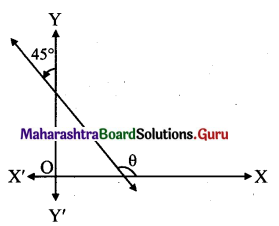
Since the line makes an angle of 45° with positive direction of Y-axis in anticlockwise direction,
Inclination of the line (0) = (90° + 45°)
∴ Slope of the line = tan(90° + 45°)
= – cot 45°
= -1
Question 8.
Find the value of k for which the points P(k, -1), Q(2,1) and R(4,5) are collinear.
Solution:
Given, points P(k, – 1), Q (2, 1) and R(4, 5) are collinear.
∴ Slope of PQ = Slope of QR .
∴ \(\frac{1-(-1)}{2-k}=\frac{5-1}{4-2}\)
∴ \(\frac{2}{2-k}=\frac{4}{2}\)
∴ 4 = 4 (2 – k)
∴ 1 = 2 – k
∴ k = 2 – 1 = 1
Question 9.
Find the acute angle between the X-axis and the line joining the points A(3, -1) and B(4, – 2).
Solution:
Given, A (3, – 1) and B (4, – 2)
Slope of AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-(-1)}{4-3}\) = – 1
But, slope of a line = tan θ
∴ tan θ = – 1
= – tan 45°
= tan (180° -45°)
… [∵ tan (180° – θ) = -tan θ]
= tan 135°
∴ θ = 135°
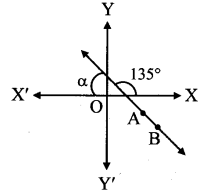
Let α be the acute angle that line AB makes with X-axis.
Then, α + 0 = 180°
α = 180°- 135° = 45°
∴ The acute angle between the X-axis and the line joining the points A and B is 45°.
![]()
Question 10.
A line passes through points A(xi, y0 and B(h, k). If the slope of the line is m, then show that k – y1 = m (h – x1).
Solution:
Given, A(x1, y1), B(h, k) and
slope of line AB = m
Slope of line AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
∴ m = \(\frac{\mathrm{k}-y_{1}}{\mathrm{~h}-x_{1}}\)
∴ k – y1 = m (h – x1)
Question 11.
If the points A(h, 0), B(0, k) and C(a, b) lie on a line, then show that \(\frac{a}{h}+\frac{b}{k}\) = 1. ‘
Solution:
Given, A(h, 0), B(0, k) and C(a, b)
Since the points A, B and C lie on a line, they are collinear.
∴ Slope of AB = slope of BC