Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 5 Straight Line Ex 5.3 Questions and Answers.
11th Maths Part 1 Straight Line Exercise 5.3 Questions And Answers Maharashtra Board
Question 1.
Write the equation of the line:
i. parallel to the X-axis and at a distance of 5 units from it and above it.
ii. parallel to the Y-axis and at a distance of 5 units from it and to the left of it.
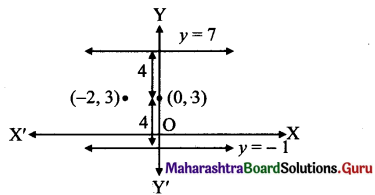
iii. parallel to the X-axis and at a distance of 4 units from the point (- 2,3).
Solution:
i. Equation of a line parallel to X-axis is y = k. Since the line is at a distance of 5 units above X-axis, k = 5
∴ The equation of the required line is y = 5.
ii. Equation of a line parallel to Y-axis is x = h. Since the line is at a distance of 5 units to the left of Y-axis, h = -5
∴ The equation of the required line is x = -5.
[Note: Answer given in the textbook is ‘y = -5
However, we found that ‘x = – 5’.]
iii. Equation of a line parallel to the X-axis is of the form y = k (k > 0 or k < 0).
Since the line is at a distance of 4 units from the point (- 2, 3),
k = 4 + 3 = 7 or k = 3- 4 = -1
∴ The equation of the required line is y = 1 or y = – 1.
![]()
Question 2.
Obtain the equation of the line:
i. parallel to the X-axis and making an intercept of 3 units on the Y-axis.
ii. parallel to the Y-axis and making an intercept of 4 units on the X-axis.
Solution:
i. Equation of a line parallel to X-axis with y-intercept ‘k’ isy = k.
Here, y-intercept = 3
∴ The equation of the required line is y = 3.
ii. Equation of a line parallel to Y-axis with x-intercept ‘h’ is x = h.
Here, x-intercept = 4
∴ The equation of the required line is x = 4.
Question 3.
Obtain the equation of the line containing the point:
i. A(2, – 3) and parallel to the Y-axis.
ii. B(4, – 3) and parallel to the X-axis.
Solution:
i. Equation of a line parallel to Y-axis is of the form x = h.
Since the line passes through A(2, – 3), h = 2
∴ The equation of the required line is x = 2.
ii. Equation of a line parallel to X-axis is of the formy = k.
Since the line passes through B(4, – 3), k = -3
∴ The equation of the required line is y = – 3.
Question 4.
Find the equation of the line:
i. passing through the points A(2, 0) and B(3,4)
ii. passing through the points P(2, 1) and Q(2,-1)
Solution:
i. The required line passes through the points A(2, 0) and B(3,4).
Equation of the line in two point form is \(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
Here, (x1y1) = (2,0) and (x1,y2) = (3,4)
∴ The equation of the required line is
∴ \(\frac{y-0}{4-0}=\frac{x-2}{3-2}\)
∴ \(\frac{y}{4}=\frac{x-2}{1}\)
∴ y = 4(x – 2)
∴ y = 4x – 8
∴ 4x – y – 8 = 0
ii. The required line passes through the points P(2, 1) and Q(2,-1).
Since both the given points have same
x co-ordinates i.e. 2,
the given points lie on the line x = 2.
∴ The equation of the required line is x = 2.
![]()
Question 5.
Find the equation of the line:
i. containing the origin and having inclination 60°.
ii. passing through the origin and parallel to AB, where A is (2,4) and B is (1,7).
iii. having slope 1/2 and containing the point (3, -2)
iv. containing the point A(3, 5) and having slope 2/3
v. containing the point A(4, 3) and having inclination 120°.
vi. passing through the origin and which bisects the portion of the line 3JC + y = 6 intercepted between the co-ordinate axes.
Solution:
i. Given, Inclination of line = θ = 60°
Slope of the line (m) = tan θ = tan 60°
= \(\sqrt{3}\)
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
.‘. The equation of the required line is y = \(\sqrt{3}\) x
ii. Given, A (2, 4) and B (1, 7)
Slope of AB = \(\frac{7-4}{1-2}\) = -3 1-2
Since the required line is parallel to line AB, slope of required line (m) = slope of AB
∴ m = – 3 and the required line passes through the origin.
Equation of the line having slope m and passing through origin (0, 0) is y = mx.
∴ The equation of the required line is y = – 3x
iii. Given, slope(m) = \(=\frac{1}{2}\) and the line passes through (3, – 2).
Equation of the line in slope point form is
y-y 1= m(x-x1)
∴ The equation of the required line is
[y-(- 2)]=\(\frac{1}{2}\)(x-3)
∴ 2(y + 2)=x – 3
∴ 2y + 4 = x – 3
∴ x – 2y – 7 = 0
iv. Given, slope(m) = \(\frac{2}{3}\) and the line passes through (3, 5).
Equation of the line in slope point form is y-y1 = m(x -x1)
∴ The equation of the required line is y – 5 = \(\frac{2}{3}\)(x-3)
∴ 3 (y – 5) = 2 (x – 3)
∴ 3y – 15 = 2x – 6
∴ 2x – 3y + 9 = 0
v. Given, Inclination of line = θ = 120°
Slope of the line (m) = tan θ = tan 120°
= tan (90° + 30°)
= – cot 30°
= – \(\sqrt{3}\)
and the line passes through A(4, 3).
Equation of the line in slope point form is y-y1 = m(x -x1)
∴ The equation of the required line is
y- 3 = –\(\sqrt{3}\)(x-4)
∴ y – 3 = –\(\sqrt{3}\) x + 4\(\sqrt{3}\)
∴ \(\sqrt{3}\)x + y – 3 -4\(\sqrt{3}\) = 0
vi.
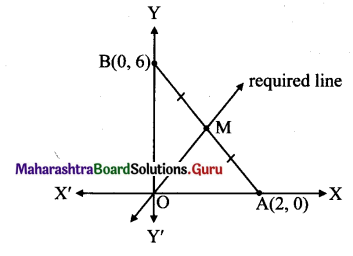
Given equation of the line is 3x +y = 6.
∴ \(\frac{x}{2}+\frac{y}{6}=1\)
This equation is of the form \(\frac{x}{\mathrm{a}}+\frac{y}{\mathrm{~b}}\) = 1,
where a = 2, b = 6
∴ The line 3x + y = 6 intersects the X-axis and Y-axis at A(2, 0) and B(0, 6) respectively. Required line is passing through the midpoint of AB.
∴ Midpoint of AB = ( \(\frac{2+0}{2}, \frac{0+6}{2}\) ) = (1,3)
∴ Required line passes through (0, 0) and (1,3).
Equation of the line in two point form is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
∴ The equation of the required line is
\(\frac{y-0}{3-0}=\frac{x-0}{1-0}\)
\(\frac{y}{3}=\frac{x}{1}\)
∴ y = 3x
∴ 3x – y = 0
Alternate Method:
Given equation of the line is 3x + y = 6 …(i)
Substitute y = 0 in (i) to get a point on X-axis.
∴ 3x + 0 = 6
∴ x = 2
Substitute x = 0 in (i) to get a point on Y-axis.
∴ 3(0) + 7 = 6
∴ y = 6
∴ The line 3x + y = 6 intersects the X-axis and Y-axis at A(2,0) and B(0,6) respectively.
Let M be the midpoint of AB.
M = \(\left(\frac{2+0}{2}, \frac{0+6}{2}\right)\) = (1,3)
Slope of OM (m) = \(\frac{3-0}{1-0}\) = 3
Equation of OM is of the formy = mx.
∴ The equation of the required line is y = 3x
∴ 3x – y = 0
![]()
Question 6.
Line y = mx + c passes through the points A(2,1) and B(3,2). Determine m and c.
Solution:
Given, A(2, 1) and B(3,2)
Equation of the line in two point form is \(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
∴ The equation of the required line is
\(\frac{y-1}{2-1}=\frac{x-2}{3-2}\)
∴ \(\frac{y-1}{1}=\frac{x-2}{1}\)
∴ y – 1 = x – 2
∴ y = x – 1
Comparing this equation with y = mx + c, we get
m = 1 and c = – 1
Alternate Method:
Points A(2, 1) and B(3, 2) lie on the line y = mx + c.
∴ They must satisfy the equation.
∴ 2m + c = 1 …(i)
and 3m + c = 2 …(ii)
equation (ii) – equation (i) gives m = 1
Substituting m = 1 in (i), we get 2(1) + c = 1
∴ c = 1 – 2 = – 1
Question 7.
Find the equation of the line having inclination 135° and making x-intercept 7.
Solution:
Given, Inclination of line = 0 = 135°
∴ Slope of the line (m) = tan 0 = tan 135°
= tan (90° + 45°)
= – cot 45° = – 1 x-intercept of the required line is 7.
∴ The line passes through (7, 0).
Equation of the line in slope point form is y – y1 = m(x – x1)
∴ The equation of the required line is y — 0 = – 1 (x – 7)
∴ y = -x + 7
∴ x + y – 7 = 0
Question 8.
The vertices of a triangle are A(3, 4), B(2, 0) and C(- 1, 6). Find the equations of the lines containing
i. side BC
ii. the median AD
iii. the midpoints of sides AB and BC.
Solution:
Vertices of AABC are A(3, 4), B(2, 0) and C(- 1, 6).
i. Equation of the line in two point form is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
∴ The equation of the side BC is
\(\frac{y-0}{6-0}=\frac{x-2}{-1-2}\)
\(\frac{y}{6}=\frac{x-2}{-3}\)
∴ – 3y = 6x – 12
∴ 6x + 3y – 12 = 0
∴ 2x + y – 4 = 0
ii. Let D be the midpoint of side BC.
Then, AD is the median through A.
∴ D = \(\left(\frac{2-1}{2}, \frac{0+6}{2}\right)=\left(\frac{1}{2}, 3\right)\)
The median AD passes through the points
A(3,4) and D( \(\frac{1}{2}\) , 3)
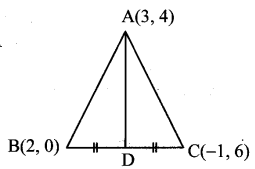
∴ The equation of the median AD is
\(\frac{y-4}{3-4}=\frac{x-3}{\frac{1}{2}-3}\)
\(\frac{y-4}{-1}=\frac{x-3}{-\frac{5}{2}}\)
\(\frac{5}{2}\)(y-4) = x – 3
∴ 5y – 20 = 2x – 6
∴ 2x – 5y + 14 = 0
iii. Let D and E be the midpoints of side AB and side BC respectively.
The equation of the line DE is
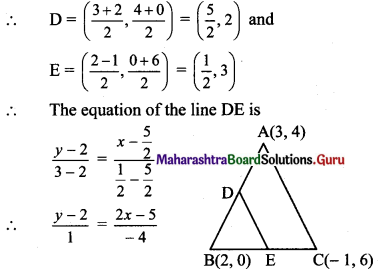
∴ -4(y-2) = 2x-5
∴ 2x + 4y – 13 = 0
Question 9.
Find the x and y-intercepts of the following lines:
i. \(\frac{x}{3}+\frac{y}{2}=1\)
ii. \(\frac{3 x}{2}+\frac{2 y}{3}=1\)
iii. 2x – 3y + 12 = 0
Solution:
i. Given equation of the line is latex]\frac{x}{3}+\frac{y}{2}=1[/latex]
This is of the form \(\frac{x}{a}+\frac{y}{b}\) = 1,
where x-intercept = a, y-intercept = b
∴ x-intercept = 3, y-intercept = 2
ii. Given equation of the line is \(\frac{3 x}{2}+\frac{2 y}{3}\) = 1
∴ \(\frac{x}{\left(\frac{2}{3}\right)}+\frac{y}{\left(\frac{3}{2}\right)}\) = 1
This is of the form = \(\frac{x}{a}+\frac{y}{b}\) = 1,
where x-intercept = a, y-intercept = b
∴ x-intercept = \(\frac{2}{3}\) and y-intercept = \(\frac{3}{2}\)
iii. Given equation of the line is 2x – 3y + 12 = 0
∴ 2x – 3y = – 12
∴ \(\frac{2 x}{(-12)}-\frac{3 y}{(-12)}=1\)
∴ \(\frac{x}{-6}+\frac{y}{4}=1\)
This is of the form \(\) = 1,
where x-intercept = a, y-intercept = b
∴ x-intercept = – 6 and y-intercept = 4
![]()
Question 10.
Find equations of the line which contains the point A(l, 3) and the sum of whose intercepts on the co-ordinate axes is zero.
Solution:
Case I: Line not passing through origin.
Let the equation of the line be
\(\frac{x}{a}+\frac{y}{b}=1\) ………..(i)
Since, the sum of the intercepts of the line is zero.
∴ a + b = 0
∴ b = – a
Substituting b = – a in (i), we get
\(\frac{x}{a}+\frac{y}{(-a)}=1\)
x – y = a .. .(ii)
Since, the line passes through A(1, 3).
∴ 1 – 3 = a
∴ a = – 2
Substituting the value of a in (ii), equation of the required line is
∴ x – y = – 2,
∴ x – y + 2 = 0
Case II: Line passing through origin.
Slope of line passing through origin and
A(1, 3) is m = \(\frac{3-0}{1-0}\) = 3
∴ Equation of the line having slope m and passing through origin (0, 0) is / = mx.
∴ The equation of the required line is y = 3x
∴ 3x – y = 0
Question 11.
Find equations of the line containing the point A(3, 4) and making equal intercepts on the co-ordinate axes.
Solution:
Case I: Line not passing through origin.
Let the equation of the line be \(\frac{x}{a}+\frac{y}{b}=1\) …………(i)
This line passes through A(3, 4).
∴ \(\frac{3}{a}+\frac{4}{b}=1\)……………..(ii)
Since, the required line make equal intercepts on the co-ordinate axes.
∴ a = b …(iii)
Substituting the value of b in (ii), we get
\(\frac{3}{a}+\frac{4}{a}=1\)
∴ \(\frac{7}{a}=1\)
∴ a = 7
∴ b = 7 …[From (iii)]
Substituting the values of a and b in (i), equation of the required line is
\(\frac{x}{7}+\frac{y}{7}=1\) = 1
∴ x + y = 7
Case II: Line passing through origin.
Slope of line passing through origin and A(3,4) is m = \(=\frac{4-0}{3-0}=\frac{4}{3}\)
∴ Equation of the line having slope m and passing through origin (0, 0) is y = mx.
∴ The equation of the required line is 4
y = \(\frac{4}{3}\)x
∴ 4x – 3y = 0
Question 12.
Find the equations of the altitudes of the triangle whose vertices are A(2, 5), B(6, – 1 ) and C(- 4, – 3).
Solution:
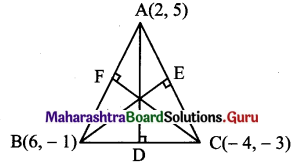
A(2, 5), B(6, – 1), C(- 4, – 3) are the vertices of ∆ABC.
Let AD, BE and CF be the altitudes through the vertices A, B and C respectively of ∆ABC.
∴ Slope of AD = -5 …[∵AD ⊥ BC]
Since altitude AD passes through (2, 5) and has slope – 5,
equation of the altitude AD is y – 5 = -5 (x – 2)
∴ y – 5 = – 5x + 10
∴ 5x +y -15 = 0
Now, slope of AC = \(\frac{-3-5}{-4-2}=\frac{-8}{-6}=\frac{4}{3}\)
Slope of BE = \(\frac{-3}{4}\)
…[∵ BE ⊥ AC]
Since altitude BE passes through (6,-1) and has slope \(\frac{-3}{4}\),
equation of the altitude BE is
y-(-1) = \(\frac{-3}{4}\) (x – 6)
∴ 4 (y + 1) = – 3 (x – 6)
∴ 4y + 4 =-3x+ 18
∴ 3x + 4y – 14 = 0
Also, slope of AB = \(\frac{-1-5}{6-2}=\frac{-6}{4}=\frac{-3}{2}\)
∴ Slope of CF = \({2}{3}\) ….[∵ CF ⊥ AB]
Since altitude CF passes through (- 4, – 3) and has slope , \(\frac{2}{3}\)
equation of the altitude CF is
y-(-3) = \(\frac{2}{3}\)[x-(-4)]
∴ 3 (y + 3) = 2 (x + 4)
∴ 3y + 9 = 2x + 8
∴ 2x – 3y – 1 = 0
![]()
Question 13.
Find the equations of perpendicular bisectors of sides of the triangle whose vertices are P(-1, 8), Q(4, – 2) and R(- 5, – 3).
Solution:
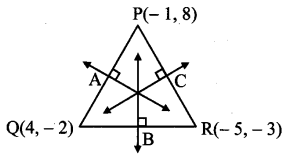
Let A, B and C be the midpoints of sides PQ, QR and PR respectively of APQR.
A is the midpoint of side PQ.
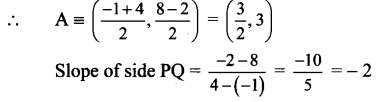
Slope of perpendicular bisector of PQ is \(\frac{1}{2}\) and it passes through (\(\frac{3}{2}\)), 3).
Equation of the perpendicular bisector of side PQ is
y – 3 = \(\frac{1}{2}\)(x – \(\frac{3}{2}\))
y – 3 = (\(\frac{1}{2}\left(\frac{2 x-3}{2}\right)\))
∴ 4(y – 3) = 2x – 3
∴ 4y – 12 = 2x – 3
∴ 2x – 4y + 9 = 0
B is the midpoint of side QR
∴ B = \(\left(\frac{4-5}{2}, \frac{-2-3}{2}\right)=\left(\frac{-1}{2}, \frac{-5}{2}\right)\)
Slope of side QR = \(\frac{-3-(-2)}{-5-4}=\frac{-1}{-9}=\frac{1}{9}\)
∴ Slope of perpendicular bisector of QR is -9 and it passes through \(\left(-\frac{1}{2},-\frac{5}{2}\right)\)
∴ Equation of the perpendicular bisector of side QR is
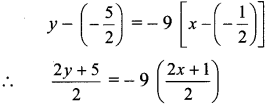
∴ 2y + 5 = -18x – 9
∴ 18x + 2y + 14 = 0
∴ 9x + y + 7 = 0
C is the midpoint of side PR.

Equation of the perpendicular bisector of PR is \(y-\frac{5}{2}=-\frac{4}{11}(x+3)\)
∴ \(11\left(\frac{2 y-5}{2}\right)\) =-4(x + 3)
∴ 11(2y – 5) = – 8 (x + 3)
∴ 22y – 55 = – 8x – 24
∴ 8x + 22y -31 = 0
Question 14.
Find the co-ordinates of the orthocentre of the triangle whose vertices are A(2, – 2), B(l, 1) and C(-1,0).
Solution:
Let O be the orthocentre of AABC.
Let AM and BN be the altitudes of sides BC and AC respectively.
Now, slope of BC = \(\frac{0-1}{-1-1}=\frac{-1}{-2}=\frac{1}{2}\)
Slope of AM = -2 ,..[∵ AM ⊥ BC]
Since AM passes through (2, – 2) and has slope -2,
equation of the altitude AM is y – (- 2) = – 2 (x – 2)
∴ y + 2 = -2x + 4
∴ 2x + y – 2 = 0 …(i)
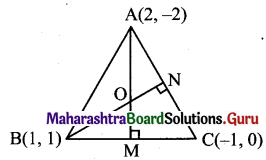
Also, slope of AC = \(\frac{0-(-2)}{-1-2}=\frac{2}{-3}\)
∴ Slope of BN = \(\frac{3}{2}\) …[∵ BN ⊥ AC]
Since BN passes through (1,1) and has slope \(\frac{3}{2}\), equation of the altitude BN is
y – 1 = \(\frac{3}{2}\)(x-1)
∴ 2y – 2 = 3x – 3
∴ 3x – 2y – 1 = 0 …(ii)
To find co-ordinates of orthocentre, we have to solve equations (i) and (ii).
By (i) x 2 + (ii), we get
7x – 5 = 0
∴ x = \(\frac{5}{7}\)
substituting x = \(\frac{5}{7}\) in eq (i), we get
2(\(\frac{5}{7}\)) + y – 2 = 0
∴ y = -2(\(\frac{5}{7}\)) + 2
∴ y = \(\frac{-10+14}{7}=\frac{4}{7}\)
∴ Coordinates of orthocentre O = \(\left(\frac{5}{7}, \frac{4}{7}\right)\)
![]()
Question 15.
N(3, – 4) is the foot of the perpendicular drawn from the origin to line L. Find the equation of line L.
Solution:
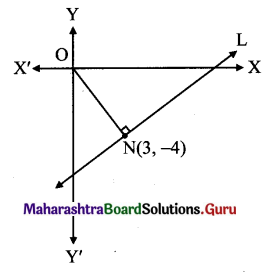
Slope of ON = \(\frac{-4-0}{3-0}=\frac{-4}{3}\)
Since line L ⊥ ON,
slope of the line L is \(\frac{3}{4}\) and it passes through point N(3, -4).
Equation of the line in slope point form is y – y1 = m(x – x1)
Equation of line L is
y-(-4) = \(\frac{3}{4}\)(x-3)
∴ 4(y + 4) = 3(x – 3)
∴ 4y + 16 = 3x – 9
∴ 3x – 4y – 25 = 0
11th Std State Board Maths Solution