Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 6 Circle Miscellaneous Exercise 6 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 6 Circle Miscellaneous Exercise 6
(I) Choose the correct alternative.
Question 1.
Equation of a circle which passes through (3, 6) and touches the axes is
(A) x2 + y2 + 6x + 6y + 3 = 0
(B) x2 + y2 – 6x – 6y – 9 = 0
(C) x2 + y2 – 6x – 6y + 9 = 0
(D) x2 + y2 – 6x + 6y – 3 = 0
Answer:
(C) x2 + y2 – 6x – 6y + 9 = 0
Question 2.
If the lines 2x – 3y = 5 and 3x – 4y = 7 are the diameters of a circle of area 154 sq. units, then find the equation of the circle.
(A) x2 + y2 – 2x + 2y = 40
(B) x2 + y2 – 2x – 2y = 47
(C) x2 + y2 – 2x + 2y = 47
(D) x2 + y2 – 2x – 2y = 40
Answer:
(C) x2 + y2 – 2x + 2y = 47
Hint:
Centre of circle = Point of intersection of diameters.
Solving 2x – 3y = 5 and 3x – 4y = 7, we get
x = 1, y = -1
Centre of the circle C(h, k) = C(1, -1)
∴ Area = 154
πr2 = 154
\(\frac{22}{7} \times r^{2}\) = 154
r2 = 154 × \(\frac{22}{7}\) = 49
∴ r = 7
equation of the circle is
(x – 1)2 + (y + 1)2 = 72
x2 + y2 – 2x + 2y = 47
![]()
Question 3.
Find the equation of the circle which passes through the points (2, 3) and (4, 5), and the center lies on the straight line y – 4x + 3 = 0.
(A) x2 + y2 – 4x – 10y + 25 = 0
(B) x2 + y2 – 4x – 10y – 25 = 0
(C) x2 + y2 – 4x + 10y – 25 = 0
(D) x2 + y2 + 4x – 10y + 25 = 0
Answer:
(A) x2 + y2 – 4x – 10y + 25 = 0
Question 4.
The equation(s) of the tangent(s) to the circle x2 + y2 = 4 which are parallel to x + 2y + 3 = 0 are
(A) x – 2y = 2
(B) x + 2y = ±2√3
(C) x + 2y = ±2√5
(D) x – 2y = ±2√5
Answer:
(C) x + 2y = ±2√5
Question 5.
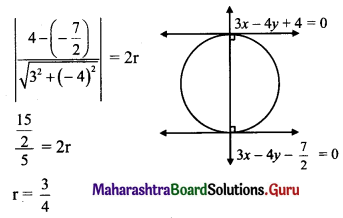
If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.
(A) \(\frac{3}{4}\)
(B) \(\frac{4}{3}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{7}{4}\)
Answer:
(A) \(\frac{3}{4}\)
Hint:
Tangents are parallel to each other.
The perpendicular distance between tangents = diameter
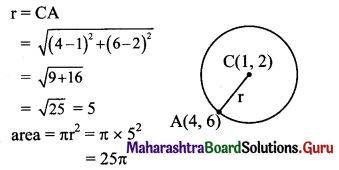
Question 6.
The area of the circle having centre at (1, 2) and passing through (4, 6) is
(A) 5π
(B) 10π
(C) 25π
(D) 100π
Answer:
(C) 25π
Hint:
![]()
Question 7.
If a circle passes through the points (0, 0), (a, 0), and (0, b), then find the co-ordinates of its centre.
(A) \(\left(\frac{-a}{2}, \frac{-b}{2}\right)\)
(B) \(\left(\frac{a}{2}, \frac{-b}{2}\right)\)
(C) \(\left(\frac{-a}{2}, \frac{b}{2}\right)\)
(D) \(\left(\frac{a}{2}, \frac{b}{2}\right)\)
Answer:
(D) \(\left(\frac{a}{2}, \frac{b}{2}\right)\)
Question 8.
The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is
(A) x2 + y2 = 9a2
(B) x2 + y2 = 16a2
(C) x2 + y2 = 4a2
(D) x2 + y2 = a2
Answer:
(C) x2 + y2 = 4a2
Hint:
Since the triangle is equilateral.
The centroid of the triangle is same as the circumcentre
and radius of the circumcircle = \(\frac{2}{3}\) (median) = \(\frac{2}{3}\)(3a) = 2a
Hence, the equation of the circumcircle whose centre is at (0, 0) and radius 2a is x2 + y2 = 4a2
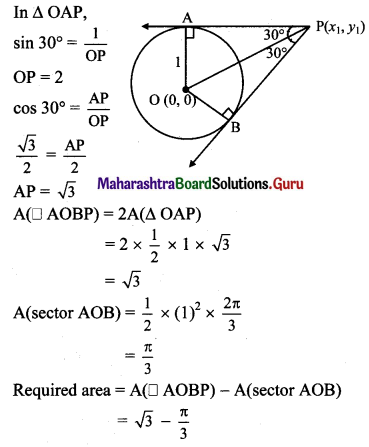
Question 9.
A pair of tangents are drawn to a unit circle with centre at the origin and these tangents intersect at A enclosing an angle of 60. The area enclosed by these tangents and the arc of the circle is
(A) \(\frac{2}{\sqrt{3}}-\frac{\pi}{6}\)
(B) \(\sqrt{3}-\frac{\pi}{3}\)
(C) \(\frac{\pi}{3}-\frac{\sqrt{3}}{6}\)
(D) \(\sqrt{3}\left(1-\frac{\pi}{6}\right)\)
Answer:
(B) \(\sqrt{3}-\frac{\pi}{3}\)
Hint:
Question 10.
The parametric equations of the circle x2 + y2 + mx + my = 0 are
(A) x = \(\frac{-m}{2}+\frac{m}{\sqrt{2}} \cos \theta\), y = \(\frac{-m}{2}+\frac{m}{\sqrt{2}} \sin \theta\)
(B) x = \(\frac{-m}{2}+\frac{m}{\sqrt{2}} \cos \theta\), y = \(\frac{+m}{2}+\frac{m}{\sqrt{2}} \sin \theta\)
(C) x = 0, y = 0
(D) x = m cos θ, y = m sin θ
Answer:
(A) x = \(\frac{-m}{2}+\frac{m}{\sqrt{2}} \cos \theta\), y = \(\frac{-m}{2}+\frac{m}{\sqrt{2}} \sin \theta\)
![]()
(II) Answer the following:
Question 1.
Find the centre and radius of the circle x2 + y2 – x + 2y – 3 = 0.
Solution:
Given equation of the circle is x2 + y2 – x + 2y – 3 = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -1, 2f = 2 and c = -3
g = \(\frac{-1}{2}\), f = 1 and c = -3
Centre of the circle = (-g, -f) = (\(\frac{1}{2}\), -1)
and radius of the circle
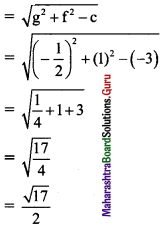
Question 2.
Find the centre and radius of the circle x = 3 – 4 sin θ, y = 2 – 4 cos θ.
Solution:
Given, x = 3 – 4 sin θ, y = 2 – 4 cos θ
⇒ x – 3 = -4 sin θ, y – 2 = -4 cos θ
On squaring and adding, we get
⇒ (x – 3)2 + (y – 2)2 = (-4 sin θ)2 + (-4 cos θ)2
⇒ (x – 3)2 + (y – 2)2 = 16 sin2 θ + 16 cos2 θ
⇒ (x – 3)2 + (y – 2)2 = 16(sin2 θ + cos2 θ)
⇒ (x – 3)2 + (y – 2)2 = 16(1)
⇒ (x – 3)2 + (y – 2)2 = 16
⇒ (x – 3)2 + (y – 2)2 = 42
Comparing this equation with (x – h)2 + (y – k)2 = r2, we get
h = 3, k = 2, r = 4
∴ Centre of the circle is (3, 2) and radius is 4.
![]()
Question 3.
Find the equation of circle passing through the point of intersection of the lines x + 3y = 0 and 2x – 7y = 0 and whose centre is the point of intersection of lines x + y + 1 = 0 and x – 2y + 4 = 0.
Solution:
Required circle passes through the point of intersection of the lines x + 3y = 0 and 2x – 7y = 0.
x + 3y = 0
⇒ x = -3y ……..(i)
2x – 7y = 0 ……(ii)
Substituting x = -3y in (ii), we get
⇒ 2(-3y) – 7y = 0
⇒ -6y – 7y = 0
⇒ -13y = 0
⇒ y = 0
Substituting y = 0 in (i), we get
x = -3(0) = 0
Point of intersection is O(0, 0).
This point O(0, 0) lies on the circle.
Let C(h, k) be the centre of the required circle.
Since, point of intersection of lines x + y = -1 and x – 2y = -4 is the centre of circle.
∴ x = h, y = k
∴ Equations of lines become
h + k = -1 ……(iii)
h – 2k = -4 …..(iv)
By (iii) – (iv), we get
3k = 3
⇒ k = 1
Substituting k = 1 in (iii), we get
h + 1 = -1
⇒ h = -2
∴ Centre of the circle is C(-2, 1) and it passes through point O(0, 0).
Radius(r) = OC
= \(\sqrt{(0+2)^{2}+(0-1)^{2}}\)
= \(\sqrt{4+1}\)
= √5
The equation of a circle with centre at (h, k) and radius r is given by
(x – h)2 + (y – k)2 = r2
Here, h = -2, k = 1
the required equation of the circle is
(x + 2)2 + (y – 1)2 = (√5)2
⇒ x2 + 4x + 4 + y2 – 2y + 1 = 5
⇒ x2 + y2 + 4x – 2y = 0
Question 4.
Find the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the positive side of the X-axis and Y-axis respectively.
Solution:
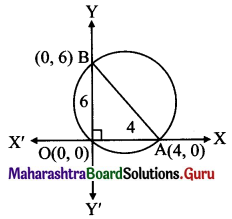
Let the circle cut the chord of length 4 on X-axis at point A and the chord of length 6 on the Y-axis at point B.
∴ the co-ordinates of point A are (4, 0) and co-ordinates of point B are (0, 6).
Since ∠BOA is a right angle.
AB represents the diameter of the circle.
The equation of a circle having (x1, y1) and (x2, y2) as endpoints of diameter is given by
(x – x1) (x – x2) + (y – y1) (y – y2) = 0
Here, x1 = 4, y1 = 0, x2 = 0, y2 = 6
∴ the required equation of the circle is
⇒ (x – 4) (x – 0) + (y – 0) (y – 6) = 0
⇒ x2 – 4x + y2 – 6y = 0
⇒ x2 + y2 – 4x – 6y = 0
![]()
Question 5.
Show that the points (9, 1), (7, 9), (-2, 12) and (6, 10) are concyclic.
Solution:
Let the equation of circle passing through the points (9, 1), (7, 9), (-2, 12) be
x2 + y2 + 2gx + 2fy + c = 0 …….(i)
For point (9, 1),
Substituting x = 9 andy = 1 in (i), we get
81 + 1 + 18g + 2f + c = 0
⇒ 18g + 2f + c = -82 …..(ii)
For point (7, 9),
Substituting x = 7 andy = 9 in (i), we get
49 + 81 + 14g + 18f + c = 0
⇒ 14g + 18f + c = -130 ……(iii)
For point (-2, 12),
Substituting x = -2 and y = 12 in (i), we get
4 + 144 – 4g + 24f + c = 0
⇒ -4g + 24f + c = -148 …..(iv)
By (ii) – (iii), we get
4g – 16f = 48
⇒ g – 4f = 12 …..(v)
By (iii) – (iv), we get
18g – 6f = 18
⇒ 3g – f = 3 ……(vi)
By 3 × (v) – (vi), we get
-11f = 33
⇒ f = -3
Substituting f = -3 in (vi), we get
3g – (-3) = 3
⇒ 3g + 3 = 3
⇒ g = 0
Substituting g = 0 and f = -3 in (ii), we get
18(0) + 2(-3) + c = – 82
⇒ -6 + c = -82
⇒ c = -76
Equation of the circle becomes
x2 + y2 + 2(0)x + 2(-3)y + (-76) = 0
⇒ x2 + y2 – 6y – 76 = 0 ……(vii)
Now for the point (6, 10),
Substituting x = 6 and y = 10 in L.H.S. of (vii), we get
L.H.S = 62 + 102 – 6(10) – 76
= 36 + 100 – 60 – 76
= 0
= R.H.S.
∴ Point (6,10) satisfies equation (vii).
∴ the given points are concyciic.
Question 6.
The line 2x – y + 6 = 0 meets the circle x2 + y2 + 10x + 9 = 0 at A and B. Find the equation of circle with AB as diameter. Solution:
2x – y + 6 = 0
⇒ y = 2x + 6
Substituting y = 2x + 6 in x2 + y2 + 10x + 9 = 0, we get
⇒ x2 + (2x + 6)2 + 10x + 9 = 0
⇒ x2 + 4x2 + 24x + 36 + 10x + 9 = 0
⇒ 5x2 + 34x + 45 = 0
⇒ 5x2 + 25x + 9x + 45 = 0
⇒ (5x + 9) (x + 5) = 0
⇒ 5x = -9 or x = -5
⇒ x = \(\frac{-9}{5}\) or x = -5
When x = \(\frac{-9}{5}\),
y = 2 × \(\frac{-9}{5}\) + 6
= \(\frac{-18}{5}\) + 6
= \(\frac{-18+30}{5}\)
= \(\frac{12}{5}\)
∴ Point of intersection is A\(\left(\frac{-9}{5}, \frac{12}{5}\right)\)
When x = -5,
y = -10 + 6 = -4
∴ Point of intersection in B (-5, -4).
By diameter form, equation of circle with AB as diameter is
(x + \(\frac{9}{5}\)) (x + 5) + (y – \(\frac{12}{5}\)) (y + 4) = 0
⇒ (5x + 9) (x + 5) + (5y – 12) (y + 4) = 0
⇒ 5x2 + 25x + 9x + 45 + 5y2 + 20y – 12y – 48 = 0
⇒ 5x2 + 5y2 + 34x + 8y – 3 = 0
![]()
Question 7.
Show that x = -1 is a tangent to circle x2 + y2 – 4x – 2y – 4 = 0 at (-1, 1).
Solution:
Given equation of circle is x2 + y2 – 4x – 2y – 4 = 0.
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -4, 2f = -2, c = -4
⇒ g = -2, f = -1, c = -4
The equation of a tangent to the circle
x2 + y2 + 2gx + 2fy + c = 0 at (x1, y1) is xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
the equation of the tangent at (-1, 1) is
⇒ x(-1) + y(1) – 2(x – 1) – 1(y + 1) – 4 = 0
⇒ -3x – 3 = 0
⇒ -x – 1 = 0
⇒ x = -1
∴ x = -1 is the tangent to the given circle at (-1, 1).
Question 8.
Find the equation of tangent to the circle x2 + y2 = 64 at the point P(\(\frac{2 \pi}{3}\)).
Solution:
Given equation of circle is x2 + y2 = 64
Comparing this equation with x2 + y2 = r2, we get r = 8
The equation of a tangent to the circle x2 + y2 = r2 at P(θ) is x cos θ + y sin θ = r
∴ the equation of the tangent at P(\(\frac{2 \pi}{3}\)) is
⇒ x cos \(\frac{2 \pi}{3}\) + y sin \(\frac{2 \pi}{3}\) = 9
⇒ \(x\left(\frac{-1}{2}\right)+y\left(\frac{\sqrt{3}}{2}\right)=8\)
⇒ -x + √3y = 16
⇒ x – √3y + 16 = 0
Question 9.
Find the equation of locus of the point of intersection of perpendicular tangents drawn to the circle x = 5 cos θ and y = 5 sin θ.
Solution:
The locus of the point of intersection of perpendicular tangents is the director circle of the given circle.
x = 5 cos θ and y = 5 sin θ
⇒ x2 + y2 = 25 cos2 θ + 25 sin2 θ
⇒ x2 + y2 = 25 (cos2 θ + sin2 θ)
⇒ x2 + y2 = 25(1) = 25
The equation of the director circle of the circle x2 + y2 = a2 is x2 + y2 = 2a2.
Here, a = 5
∴ the required equation is
x2 + y2 = 2(5)2 = 2(25)
∴ x2 + y2 = 50
![]()
Question 10.
Find the equation of the circle concentric with x2 + y2 – 4x + 6y = 1 and having radius 4 units.
Solution:
Given equation of circle is
x2 + y2 – 4x + 6y = 1 i.e., x2 + y2 – 4x + 6y – 1 = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -4, 2f = 6
⇒ g = -2, f = 3
Centre of the circle = (-g, -f) = (2, -3)
Given circle is concentric with the required circle.
∴ They have same centre.
∴ Centre of the required circle = (2, -3)
The equation of a circle with centre at (h, k) and radius r is (x – h)2 + (y – k)2 = r2
Here, h = 2, k = -3 and r = 4
∴ the required equation of the circle is
(x – 2)2 + [y – (-3)]2 = 42
⇒ (x – 2)2 + (y + 3)2 = 16
⇒ x2 – 4x + 4 + y2 + 6y + 9 – 16 = 0
⇒ x2 + y2 – 4x + 6y – 3 = 0
Question 11.
Find the lengths of the intercepts made on the co-ordinate axes, by the circles.
(i) x2 + y2 – 8x + y – 20 = 0
(ii) x2 + y2 – 5x + 13y – 14 = 0
Solution:
To find x-intercept made by the circle x2 + y2 + 2gx + 2fy + c = 0,
substitute y = 0 and get a quadratic equation in x, whose roots are, say, x1 and x2.
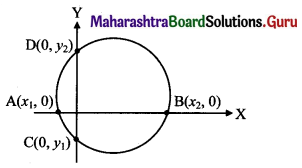
These values represent the abscissae of ends A and B of the x-intercept.
Length of x-intercept = |AB| = |x2 – x1|
Similarly, substituting x = 0, we get a quadratic equation in y whose roots, say, y1 and y2 are ordinates of the ends C and D of the y-intercept.
Length of y-intercept = |CD| = |y2 – y1|
(i) Given equation of the circle is
x2 + y2 – 8x + y – 20 = 0 ……(i)
Substituting y = 0 in (i), we get
x2 – 8x – 20 = 0 ……(ii)
Let AB represent the x-intercept, where
A = (x1, 0), B = (x2, 0)
Then from (ii),
x1 + x2 = 8 and x1x2 = -20
(x1 – x2)2 = (x1 + x2)2 – 4x1x2
= (8)2 – 4(-20)
= 64 + 80
= 144
∴ |x1 – x2| = \(\sqrt{\left(x_{1}-x_{2}\right)^{2}}\) = √144 = 12
∴ Length of x – intercept =12 units
Substituting x = 0 in (i), we get
y2 + y – 20 = 0 …..(iii)
Let CD represent the y – intercept,
where C = (0, y1) and D = (0, y2)
Then from (iii),
y1 + y2 = -1 and y1y2 = -20
(y1 – y2)2 = (y1 + y2)2 – 4y1y2
= (-1)2 – 4(-20)
= 1 + 80
= 81
∴ |y1 – y2| = \(\sqrt{\left(y_{1}-y_{2}\right)^{2}}\) = √81 = 9
∴ Length of y – intercept = 9 units.
Alternate Method:
Given equation of the circle is x2 + y2 – 8x + y – 20 = 0 ……(i)
x-intercept:
Substituting y = 0 in (i), we get
x2 – 8x – 20 = 0
⇒ (x – 10)(x + 2) = 0
⇒ x = 10 or x = -2
length of x-intercept = |10 – (-2)| = 12 units
y-intercept:
Substituting x = 0 in (i), we get
y2 + y – 20 = 0
⇒ (y + 5)(y – 4) = 0
⇒ y = -5 or y = 4
length of y-intercept = |-5 – 4| = 9 units
![]()
(ii) Given equation of the circle is
x2 + y2 – 5x + 13y – 14 = 0
Substituting y = 0 in (i), we get
x2 – 5x – 14 = 0 ……(ii)
Let AB represent the x-intercept, where
A = (x1, 0), B = (x2, 0)
Then from (ii),
x1 + x2 = 5 and x1x2 = -14
(x1 – x2)2 = (x1 + x2)2 – 4x1x2
= (5)2 – 4(-14)
= 25 + 56
= 81
∴ |x1 – x2| = \(\sqrt{\left(x_{1}-x_{2}\right)^{2}}\) = √81 = 9
∴ Length of x-intercept = 9 units
Substituting x = 0 in (i), we get
y2 + 13y – 14 = 0 ……(iii)
Let CD represent they-intercept,
where C = (0, y1), D = (0, y2).
Then from (iii),
y1 + y2 = -13 and y1y2 = -14
(y1 – y2)2 = (y1 + y2)2 – 4y1y2
= (-13)2 – 4(-14)
= 169 + 56
= 225
∴ |y1 – y2| = \(\sqrt{\left(y_{1}-y_{2}\right)^{2}}\) = √225 = 15
∴ Length ofy-intercept = 15 units
Question 12.
Show that the circles touch each other externally. Find their point of contact and the equation of their common tangent.
(i) x2 + y2 – 4x + 10y + 20 = 0
x2 + y2 + 8x – 6y – 24 = 0
(ii) x2 + y2 – 4x – 10y + 19 = 0
x2 + y2 + 2x + 8y – 23 = 0
Solution:
(i) Given equation of the first circle is x2 + y2 – 4x + 10y + 20 = 0
Here, g = -2, f = 5, c = 20
Centre of the first circle is C1 = (2, -5)
Radius of the first circle is
r1 = \(\sqrt{(-2)^{2}+5^{2}-20}\)
= \(\sqrt{4+25-20}\)
= √9
= 3
Given equation of the second circle is x2 + y2 + 8x – 6y – 24 = 0
Here, g = 4, f = -3, c = -24
Centre of the second circle is C2 = (-4, 3)
Radius of the second circle is
r2 = \(\sqrt{4^{2}+(-3)^{2}+24}\)
= \(\sqrt{16+9+24}\)
= √49
= 7
By distance formula,
C1C2 = \(\sqrt{(-4-2)^{2}+[3-(-5)]^{2}}\)
= \(\sqrt{36+64}\)
= √1oo
= 10
r1 + r2 = 3 + 7 = 10
Since, C1C2 = r1 + r2
∴ the given circles touch each other externally.
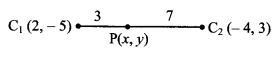
Let P(x, y) be the point of contact.
∴ P divides C1C2 internally in the ratio r1 : r2 i.e. 3 : 7.
∴ By internal division,

Equation of common tangent is
(x2 + y2 – 4x + 10y + 20) – (x2 + y2 + 8x – 6y – 24) = 0
⇒ -4x + 10y + 20 – 8x + 6y + 24 = 0
⇒ -12x + 16y + 44 = 0
⇒ 3x – 4y – 11 = 0
(ii) Given equation of the first circle is x2 + y2 – 4x – 10y + 19 = 0
Here, g = -2, f = -5, c = 19
Centre of the first circle is C1 = (2, 5)
Radius of the first circle is
r1 = \(\sqrt{(-2)^{2}+(-5)^{2}-19}\)
= \(\sqrt{4+25-19}\)
= √10
Given equation of the second circle is x2 + y2 + 2x + 8y – 23 = 0
Here, g = 1, f = 4, c = -23
Centre of the second circle is C2 = (-1, -4)
Radius of the second circle is
r2 = \(\sqrt{(-1)^{2}+4^{2}+23}\)
= \(\sqrt{1+16+23}\)
= √40
= 2√10
By distance formula,
C1C2 = \(\sqrt{(-1-2)^{2}+(-4-5)^{2}}\)
= \(\sqrt{9+81}\)
= √90
= 3√10
r1 + r2 = √10 + 2√10 = 3√10
Since, C1C2 = r1 + r2
the given circles touch each other externally.
r1 : r2 = √10 : 2√10 = 1 : 2
Let P(x, y) be the point of contact.
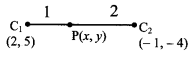
∴ P divides C1 C2 internally in the ratio r1 : r2 i.e. 1 : 2
∴ By internal division,
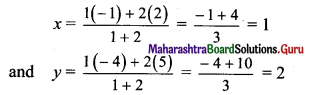
Point of contact = (1, 2)
Equation of common tangent is
(x2 + y2 – 4x – 10y + 19) – (x2 + y2 + 2x + 8y – 23) = 0
⇒ -4x – 10y + 19 – 2x – 8y + 23 = 0
⇒ -6x – 18y + 42 = 0
⇒ x + 3y – 7 = 0
![]()
Question 13.
Show that the circles touch each other internally. Find their point of contact and the equation of their common tangent.
(i) x2 + y2 – 4x – 4y – 28 = 0,
x2 + y2 – 4x – 12 = 0
(ii) x2 + y2 + 4x – 12y + 4 = 0,
x2 + y2 – 2x – 4y + 4 = 0
Solution:
(i) Given equation of the first circle is x2 + y2 – 4x – 4y – 28 = 0
Here, g = -2, f = -2, c = -28
Centre of the first circle is C1 = (2, 2)
Radius of the first circle is
r1 = \(\sqrt{(-2)^{2}+(-2)^{2}+28}\)
= \(\sqrt{4+4+28}\)
= √36
= 6
Given equation of the second circle is x2 + y2 – 4x – 12 = 0
Here, g = -2, f = 0, c = -12
Centre of the second circle is C2 = (2, 0)
Radius of the second circle is
r2 = \(\sqrt{(-2)^{2}+0^{2}+12}\)
= \(\sqrt{4+12}\)
= √16
= 4
By distance formula,
C1C2 = \(\sqrt{(2-2)^{2}+(0-2)^{2}}\)
= √4
= 2
|r1 – r2| = 6 – 4 = 2
Since, C1C2 = |r1 – r2|
∴ the given circles touch each other internally.
Equation of common tangent is
(x2 + y2 – 4x – 4y – 28) – (x2 + y2 – 4x – 12) = 0
⇒ -4x – 4y – 28 + 4x + 12 = 0
⇒ -4y – 16 = 0
⇒ y + 4 = 0
⇒ y = -4
Substituting y = -4 in x2 + y2 – 4x – 12 = 0, we get
⇒ x2 + (-4)2 – 4x – 12 = 0
⇒ x2 + 16 – 4x – 12 = 0
⇒ x2 – 4x + 4 = 0 .
⇒ (x – 2)2 = 0
⇒ x = 2
∴ Point of contact is (2, -4) and equation of common tangent is y + 4 = 0.
(ii) Given equation of the first circle is x2 + y2 + 4x – 12y + 4 = 0
Here, g = 2, f = -6, c = 4
Centre of the first circle is C1 = (-2, 6)
Radius of the first circle is
r1 = \(\sqrt{2^{2}+(-6)^{2}-4}\)
= \(\sqrt{4+36-4}\)
= √36
= 6
Given equation of the second circle is x2 + y2 – 2x – 4y + 4 = 0
Here, g = -1, f = -2, c = 4
Centre of the second circle is C2 = (1, 2)
Radius of the second circle is
r2 = \(\sqrt{(-1)^{2}+(-2)^{2}-4}\)
= \(\sqrt{1+4-4}\)
= √1
= 1
By distance formula,
C1C2 = \(\sqrt{[1-(-2)]^{2}+(2-6)^{2}}\)
= \(\sqrt{9+16}\)
= √25
= 5
|r1 – r2| = 6 – 1 = 5
Since, C1C2 = |r1 – r2|
the given circles touch each other internally.
Equation of common tangent is
(x2 + y2 + 4x – 12y + 4) – (x2 + y2 – 2x – 4y + 4) = 0
⇒ 4x – 12y + 4 + 2x + 4y – 4 = 0
⇒ 6x – 8y = 0
⇒ 3x – 4y = 0
⇒ y = \(\frac{3 x}{4}\)
Substituting y = \(\frac{3 x}{4}\) in x2 + y2 – 2x – 4y + 4 = 0, we get

∴ Point of contact is \(\left(\frac{8}{5}, \frac{6}{5}\right)\) and equation of common tangent is 3x – 4y = 0.
Question 14.
Find the length of the tangent segment drawn from the point (5, 3) to the circle x2 + y2 + 10x – 6y – 17 = 0.
Solution:
Given equation of circle is x2 + y2 + 10x – 6y – 17 = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = 10, 2f = -6, c = -17
⇒ g = 5, f = -3, c = -17
Centre of circle = (-g, -f) = (-5, 3)
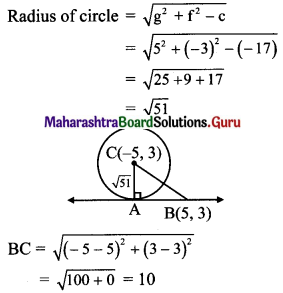
In right angled ∆ABC,
BC2 = AB2 + AC2 …..[Pythagoras theorem]
⇒ (10)2 = AB2+ (√51)2
⇒ AB2 = 100 – 51 = √49
⇒ AB = 7
∴ Length of the tangent segment from (5, 3) is 7 units.
Alternate method:
Given equation of circle is x2 + y2 + 10x – 6y – 17 = 0
Here, g = 5, f = -3, c = -17
Length of the tangent segment to the circle x2 + y2 + 2gx + 2fy + c = 0 from the point (x1, y1) is \(\sqrt{x_{1}^{2}+y_{1}^{2}+2 g x_{1}+2 f y_{1}+c}\)
Length of the tangent segment from (5, 3)
= \(\sqrt{(5)^{2}+(3)^{2}+10(5)-6(3)-17}\)
= \(\sqrt{25+9+50-18-17}\)
= √49
= 7 units
![]()
Question 15.
Find the value of k, if the length of the tangent segment from the point (8, -3) to the circle x2 + y2 – 2x + ky – 23 = 0 is √10.
Solution:
Given equation of the circle is x2 + y2 – 2x + ky – 23 = 0
Here, g = -1, f = \(\frac{\mathrm{k}}{2}\), c = -23
Length of the tangent segment to the circle x2 + y2 + 2gx + 2fy + c = 0 from the point (x1, y1) is \(\sqrt{x_{1}^{2}+y_{1}^{2}+2 g x_{1}+2 f y_{1}+c}\)
Length of the tangent segment from (8, -3) = √10
⇒ \(\sqrt{8^{2}+(-3)^{2}-2(8)+k(-3)-23}=\sqrt{10}\)
⇒ 64 + 9 – 16 – 3k – 23 = 10 …..[Squaring both the sides]
⇒ 34 – 3k = 10
⇒ 3k = 24
⇒ k = 8
Question 16.
Find the equation of tangent to circle x2 + y2 – 6x – 4y = 0, at the point (6, 4) on it.
Solution:
Given equation of the circle is x2 + y2 – 6x – 4y = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -6, 2f = -4, c = 0
⇒ g = -3, f = -2, c = 0
The equation of a tangent to the circle x2 + y2 + 2gx + 2fy + c = 0 at (x1, y1) is
xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
the equation of the tangent at (6, 4) is
x(6) + y(4) – 3(x + 6) – 2(y + 4) + 0 = 0
⇒ 6x + 4y – 3x – 18 – 2y – 8 = 0
⇒ 3x + 2y – 26 = 0
Alternate method:
Given equation of the circle is x2 + y2 – 6x – 4y = 0
x(x – 6) + y(y – 4) = 0, which is in diameter form where (0, 0) and (6, 4) are endpoints of diameter.
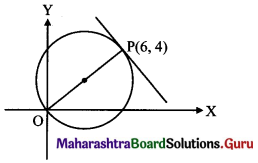
Slope of OP = \(\frac{4-0}{6-0}=\frac{2}{3}\)
Since, OP is perpendicular to the required tangent.
Slope of the required tangent = \(\frac{-3}{2}\)
the equation of the tangent at (6, 4) is
y – 4 = \(\frac{-3}{2}\) (x – 6)
⇒ 2(y – 4) = 3(x – 6)
⇒ 2y – 8 = -3x + 18
⇒ 3x + 2y – 26 = 0
Question 17.
Fihd the equation of tangent to circle x2 + y2 = 5, at the point (1, -2) on it.
Solution:
Given equation of the circle is x2 + y2 = 5
Comparing this equation with x2 + y2 = r2, we get
r2 = 5
The equation of a tangent to the circle x2 + y2 = r2 at (x1, y1) is xx1 + yy1 = r2
the equation of the tangent at (1, -2) is
x(1) + y(-2) = 5
⇒ x – 2y = 5
Question 18.
Find the equation of tangent to circle x = 5 cos θ, y = 5 sin θ, at the point θ = \(\frac{\pi}{3}\) on it.
Solution:
The equation of a tangent to the circle x2 + y2 = r2 at P(θ) is x cos θ + y sin θ = r
Here, r = 5, θ = \(\frac{\pi}{3}\)
the equation of the tangent at P(\(\frac{\pi}{3}\)) is
x cos \(\frac{\pi}{3}\) + y sin \(\frac{\pi}{3}\) = 5
⇒ \(x\left(\frac{1}{2}\right)+y\left(\frac{\sqrt{3}}{2}\right)=5\)
⇒ x + √3y = 10
![]()
Question 19.
Show that 2x + y + 6 = 0 is a tangent to x2 + y2 + 2x – 2y – 3 = 0. Find its point of contact.
Solution:
Given equation of circle is
x2 + y2 + 2x – 2y – 3 = 0 ….(i)
Given equation of line is 2x + y + 6 = 0
y = -6 – 2x ……(ii)
Substituting y = -6 – 2x in (i), we get
x + (-6 – 2x)2 + 2x – 2(-6 – 2x) – 3 = 0
⇒ x2 + 36 + 24x + 4x2 + 2x + 12 + 4x – 3 = 0
⇒ 5x2 + 30x + 45 = 0
⇒ x2 + 6x + 9 = 0
⇒ (x + 3)2 = 0
⇒ x = -3
Since, the roots are equal.
∴ 2x + y + 6 = 0 is a tangent to x2 + y2 + 2x – 2y – 3 = 0
Substituting x = -3 in (ii), we get
y = -6 – 2(-3) = -6 + 6 = 0
Point of contact = (-3, 0)
Question 20.
If the tangent at (3, -4) to the circle x2 + y2 = 25 touches the circle x2 + y2 + 8x – 4y + c = 0, find c.
Solution:
The equation of a tangent to the circle
x2 + y2 = r2 at (x1, y1) is xx1 + yy1 = r2
Equation of the tangent at (3, -4) is
x(3) + y(-4) = 25
⇒ 3x – 4y – 25 = 0 ……(i)
Given equation of circle is x2 + y2 + 8x – 4y + c = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = 8, 2f = -4
⇒ g = 4, f = -2
∴ C = (-4, 2) and r = \(\sqrt{4^{2}+(-2)^{2}-c}=\sqrt{20-c}\)
Since line (i) is a tangent to this circle also, the perpendicular distance from C(-4, 2) to line (i) is equal to radius r.

Question 21.
Find the equations of the tangents to the circle x2 + y2 = 16 with slope -2.
Solution:
Given equation of the circle is x2 + y2 = 16
Comparing this equation with x2 + y2 = a2, we get
a2 = 16
Equations of the tangents to the circle x2 + y2 = a2 with slope m are
\(y=m x \pm \sqrt{a^{2}\left(1+m^{2}\right)}\)
Here, m = -2, a2 = 16
the required equations of the tangents are
y = \(-2 x \pm \sqrt{16\left[1+(-2)^{2}\right]}\)
⇒ y = \(-2 x \pm \sqrt{16(5)}\)
⇒ y = -2x ± 4√5
⇒ 2x + y ± 4√5 = 0
![]()
Question 22.
Find the equations of the tangents to the circle x2 + y2 = 4 which are parallel to 3x + 2y + 1 = 0.
Solution:
Given equation of the circle is x2 + y2 = 4
Comparing this equation with x2 + y2 = a2, we get
a2 = 4
Given equation of the line is 3x + 2y + 1 = 0
Slope of this line = \(\frac{-3}{2}\)
Since, the required tangents are parallel to the given line.
Slope of required tangents (m) = \(\frac{-3}{2}\)
Equations of the tangents to the circle x2 + y2 = a2 with slope m are
y = mx ± \(\sqrt{\mathrm{a}^{2}\left(1+\mathrm{m}^{2}\right)}\)
the required equations of the tangents are
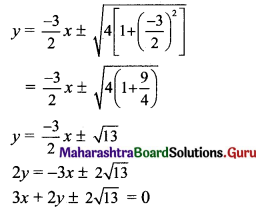
Question 23.
Find the equations of the tangents to the circle x2 + y2 = 36 which are perpendicular to the line 5x + y = 2.
Solution:
Given equation of the circle is x2 + y2 = 36
Comparing this equaiton with x2 + y2 = a2, we get
a2 = 36
Given equation of line is 5x + y = 2
Slope of this line = -5
Since, the required tangents are perpendicular to the given line.
Slope of required tangents (m) = \(\frac{1}{5}\)
Equations of the tangents to the circle x2 + y2 = a2 with slope m are
y = mx ± \(\sqrt{\mathrm{a}^{2}\left(1+\mathrm{m}^{2}\right)}\)
the required equations of the tangents are

Question 24.
Find the equations of the tangents to the circle x2 + y2 – 2x + 8y – 23 = 0 having slope 3.
Solution:
Let the equation of the tangent with slope 3 be y = 3x + c.
3x – y + c = 0 ……(i)
Given equation of circle is x2 + y2 – 2x + 8y – 23 = 0
Comparing this equation with x2 + y2 + 2gx + 2fy + c = 0, we get
2g = -2, 2f = 8, c = -23
g = -1, f = 4, c = -23
The centre of the circle is C(1, -4)
and its radius = \(\sqrt{1+16+23}\)
= √40
= 2√10
Since line (i) is a tangent to this circle the perpendicular distance from C(1, -4) to line (i) is equal to radius r.
\(\left|\frac{3(1)+4+c}{\sqrt{9+1}}\right|\) = 2√10
⇒ \(\left|\frac{7+c}{\sqrt{10}}\right|\) = 2√10
⇒ (7 + c) = ± 20
⇒ 7 + c = 20 or 7 + c = -20
⇒ c = 13 or c = – 27
∴ Equations of the tangents are 3x – y + 13 = 0 and 3x – y – 21 = 0
![]()
Question 25.
Find the equation of the locus of a point, the tangents from which to the circle x2 + y2 = 9 are at right angles.
Solution:
Given equation of the circle is x2 + y2 = 9
Comparing this equation with x2 + y2 = a2, we get
a2 = 9
The locus of the point of intersection of perpendicular tangents is the director circle of the given circle.
The equation of the director circle of the circle x2 + y2 = a2 is x2 + y2 = 2a2.
the required equation is
x2 + y2 = 2(9)
x2 + y2 = 18
Alternate method:
Given equation of the circle is x2 + y2 = 9
Comparing this equation with x2 + y2 = a2, we get a2 = 9
Let P(x1, y1) be a point on the required locus.
Equations of the tangents to the circle x2 + y2 = a2 with slope m are
y = mx ± \(\sqrt{\mathrm{a}^{2}\left(1+\mathrm{m}^{2}\right)}\)
∴ Equations of the tangents are
y = mx ± \(\sqrt{9\left(\mathrm{~m}^{2}+1\right)}\)
⇒ y = mx ± 3\(\sqrt{1+m^{2}}\)
Since, these tangents pass through (x1, y1).
y1 = mx1 ± 3\(\sqrt{1+m^{2}}\)
⇒ y1 – mx1 = ± 3\(\sqrt{1+m^{2}}\)
⇒ (y1 – mx1)2 = 9(1 + m2) ……[Squaring both the sides]
⇒ \(y_{1}^{2}-2 m x_{1} y_{1}+m^{2} x_{1}^{2}=9+9 m^{2}\)
⇒ \(\left(x_{1}^{2}-9\right) \mathrm{m}^{2}-2 \mathrm{~m} x_{1} y_{1}+\left(y_{1}^{2}-9\right)=0\)
This is a quadratic equation which has two roots m1 and m2.
m1m2 = \(\frac{y_{1}^{2}-9}{x_{1}^{2}-9}\)
Since, the tangents are at right angles.
m1m2 = -1
⇒ \(\frac{y_{1}^{2}-9}{x_{1}^{2}-9}=-1\)
⇒ \(y_{1}^{2}-9=9-x_{1}^{2}\)
⇒ \(x_{1}^{2}+y_{1}^{2}=18\)
Equation of the locus of point P is x2 + y2 = 18.
![]()
Question 26.
Tangents to the circle x2 + y2 = a2 with inclinations, θ1 and θ2 intersect in P. Find the locus of P such that
(i) tan θ1 + tan θ2 = 0
(ii) cot θ1 + cot θ2 = 5
(iii) cot θ1 . cot θ2 = c
Solution:
Let P(x1, y1) be a point on the required locus.
Equations of the tangents to the circle x2 + y2 = a2 with slope m are
y = mx ± \(\sqrt{\mathrm{a}^{2}\left(1+\mathrm{m}^{2}\right)}\)
Since, these tangents pass through (x1, y1).


