Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 7 Conic Sections Ex 7.1 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 7 Conic Sections Ex 7.1
Question 1.
Find co-ordinates of focus, equation of directrix, length of latus rectum and the co-ordinates of end points of latus rectum of the parabola:
(i) 5y2 = 24x
(ii) y2 = -20x
(iii) 3x2 = 8y
(iv) x2 = -8y
(v) 3y2 = -16x
Solution:
(i) Given equation of the parabola is 5y2 = 24x.
⇒ y2 = \(\frac{24}{5}\)x
Comparing this equation with y2 = 4ax, we get
⇒ 4a = \(\frac{24}{5}\)
⇒ a = \(\frac{6}{5}\)
Co-ordinates of focus are S(a, 0), i.e., S(\(\frac{6}{5}\), 0)
Equation of the directrix is x + a = 0.
⇒ x + \(\frac{6}{5}\) = 0
⇒ 5x + 6 = 0
Length of latus rectum = 4a
= 4(\(\frac{6}{5}\))
= \(\frac{24}{5}\)
Co-ordinates of end points of latus rectum are (a, 2a) and (a, -2a),
⇒ \(\left(\frac{6}{5}, \frac{12}{5}\right)\) and \(\left(\frac{6}{5}, \frac{-12}{5}\right)\)
(ii) Given equation of the parabola is y2 = -20x.
Comparing this equation with y2 = -4ax, we get
⇒ 4a = 20
⇒ a = 5
Co-ordinates of focus are S(-a, 0), i.e., S(-5, 0)
Equation of the directrix is x – a = 0
⇒ x – 5 = 0
Length of latus rectum = 4a = 4(5) = 20
Co-ordinates of end points of latus rectum are (-a, 2a) and (-a, -2a),
⇒ (-5, 10) and (-5, -10).
![]()
(iii) Given equation of the parabola is 3x2 = 8y
⇒ x2 = \(\frac{8}{3}\) y
Comparing this equation with x2 = 4by, we get
⇒ 4b = \(\frac{8}{3}\)
⇒ b = \(\frac{2}{3}\)
Co-ordinates of focus are S(0, b), i.e., S(0, \(\frac{2}{3}\))
Equation of the directrix is y + b = 0,
⇒ y + \(\frac{2}{3}\) = 0
⇒ 3y + 2 = 0
Length of latus rectum = 4b = 4(\(\frac{2}{3}\)) = \(\frac{8}{3}\)
Co-ordinates of end points of latus rectum are (2b, b) and (-2b, b),
⇒ \(\left(\frac{4}{3}, \frac{2}{3}\right)\) and \(\left(-\frac{4}{3}, \frac{2}{3}\right)\).
(iv) Given equation of the parabola is x2 = -8y.
Comparing this equation with x2 = -4by, we get
⇒ 4b = 8
⇒ b = 2
Co-ordinates of focus are S(0, -b), i.e., S(0, – 2)
Equation of the directrix is y – b = 0, i.e., y – 2 = 0
Length of latus rectum = 4b = 4(2) = 8
∴ Co-ordinates of end points of latus rectum are (2b, -b) and (-2b, -b), i.e., (4, -2) and (-4, -2).
(v) Given equation of the parabola is 3y2 = -16x.
⇒ y2 = \(-\frac{16}{3}\)x
Comparing this equation withy = -4ax, we get
⇒ 4a = \(\frac{16}{3}\)
⇒ a = \(\frac{4}{3}\)
Co-ordinates of focus are S(-a, 0), i.e., (\(-\frac{4}{3}\), 0)
Equation of the directrix is x – a = 0,
⇒ x – \(-\frac{4}{3}\) = 0
⇒ 3x – 4 = 0
Length of latus rectum = 4a = 4(\(\frac{4}{3}\)) = \(\frac{16}{3}\)
Co-ordinates of end points of latus rectum are (-a, 2a) and (-a, -2a),
i.e., \(\left(-\frac{4}{3}, \frac{8}{3}\right)\) and \(\left(-\frac{4}{3},-\frac{8}{3}\right)\)
![]()
Question 2.
Find the equation of the parabola with vertex at the origin, the axis along the Y-axis, and passing through the point (-10, -5).
Solution:
Vertex of the parabola is at origin (0, 0) and its axis is along Y-axis.
Equation of the parabola can be either x2 = 4by or x2 = -4by
Since the parabola passes through (-10, -5), it lies in 3rd quadrant.
Required parabola is x2 = -4by.
Substituting x = -10 and y = -5 in x2 = -4by, we get
⇒ (-10)2 = -4b(-5)
⇒ b = \(\frac{100}{20}\) = 5
∴ The required equation of the parabola is x2 = -4(5)y, i.e., x2 = -20y.
Question 3.
Find the equation of the parabola with vertex at the origin, the axis along the X-axis, and passing through the point (3, 4).
Solution:
Vertex of the parabola is at the origin (0, 0) and its axis is along X-axis.
Equation of the parabola can be either y2 = 4ax or y2 = -4ax.
Since the parabola passes through (3, 4), it lies in the 1st quadrant.
Required parabola is y2 = 4ax.
Substituting x = 3 and y = 4 in y2 = 4ax, we get
⇒ (4)2 = 4a(3)
⇒ a = \(\frac{16}{12}=\frac{4}{3}\)
The required equation of the parabola is
y2 = 4(\(\frac{4}{3}\))x
⇒ 3y2 = 16x
Question 4.
Find the equation of the parabola whose vertex is O(0, 0) and focus at (-7, 0).
Solution:
Focus of the parabola is S(-7, 0) and vertex is O(0, 0).
Since focus lies on X-axis, it is the axis of the parabola.
Focus S(-7, 0) lies on the left-hand side of the origin.
It is a left-handed parabola.
Required parabola is y = -4ax.
Focus is S(-a, 0).
a = 7
∴ The required equation of the parabola is y2 =-4(7)x, i.e., y2 = -28x.
![]()
Question 5.
Find the equation of the parabola with vertex at the origin, the axis along X-axis, and passing through the point
(i) (1, -6)
(ii) (2, 3)
Solution:
(i) Vertex of the parabola is at origin (0, 0) and its axis is along X-axis.
Equation of the parabola can be either y2 = 4ax or y2 = -4ax.
Since the parabola passes through (1, -6), it lies in the 4th quadrant.
Required parabola is y2 = 4ax.
Substituting x = 1 and y = -6 in y2 = 4ax, we get
⇒ (-6)2 = 4a(1)
⇒ 36 = 4a
⇒ a = 9
∴ The required equation of the parabola is y2 = 4(9)x, i.e., y2 = 36x.
(ii) Vertex of the parabola is at origin (0, 0) and its axis is along X-axis.
Equation of the parabola can be either y2 = 4ax or y2 = -4ax.
Since the parabola passes through (2, 3), it lies in 1st quadrant.
∴ Required parabola is y2 = 4ax.
Substituting x = 2 and y = 3 in y2 = 4ax, we get
⇒ (3)2 = 4a(2)
⇒ 9 = 8a
⇒ a = \(\frac{9}{8}\)
The required equation of the parabola is
y2 = 4(\(\frac{9}{8}\))x
⇒ y2 = \(\frac{9}{2}\) x
⇒ 2y2 = 9x.
Question 6.
For the parabola 3y2 = 16x, find the parameter of the point:
(i) (3, -4)
(ii) (27, -12)
Solution:
Given the equation of the parabola is 3y2 = 16x.
⇒ y2 = \(\frac{16}{3}\)x
Comparing this equation with y2 = 4ax, we get
⇒ 4a = \(\frac{16}{3}\)
⇒ a = \(\frac{4}{3}\)
If t is the parameter of the point P on the parabola, then
P(t) = (at2, 2at)
i.e., x = at2 and y = 2at ………(i)
(i) Given point is (3, -4)
Substituting x = 3, y = -4 and a = \(\frac{4}{3}\) in (i), we get
3 = \(\frac{4}{3}\) t2 and -4 = 2(\(\frac{4}{3}\)) t
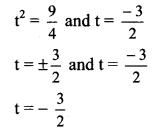
∴ The parameter of the given point is \(\frac{-3}{2}\)
(ii) Given point is (27, -12)
Substituting x = 27, y = -12 and a = \(\frac{4}{3}\) in (i), we get

∴ The parameter of the given point is \(\frac{-9}{2}\)
![]()
Question 7.
Find the focal distance of a point on the parabola y2 = 16x whose ordinate is 2 times the abscissa.
Solution:
Given the equation of the parabola is y2 = 16x.
Comparing this equation with y2 = 4ax, we get
⇒ 4a = 16
⇒ a = 4
Since ordinate is 2 times the abscissa,
y = 2x
Substituting y = 2x in y2 = 16x, we get
⇒ (2x)2 = 16x
⇒ 4x2 = 16x
⇒ 4x2 – 16x = 0
⇒ 4x(x – 4) = 0
⇒ x = 0 or x = 4
When x = 4,
focal distance = x + a = 4 + 4 = 8
When x = 0,
focal distance = a = 4
∴ Focal distance is 4 or 8.
Question 8.
Find coordinates of the point on the parabola. Also, find focal distance.
(i) y2 = 12x whose parameter is \(\frac{1}{3}\)
(ii) 2y2 = 7x whose parameter is -2
Solution:
(i) Given equation of the parabola is y2 = 12x.
Comparing this equation with y2 = 4ax, we get
⇒ 4a = 12
⇒ a = 3
If t is the parameter of the point P on the parabola, then
P(t) = (at2, 2at)
i.e., x = at2 and y = 2at ……..(i)
Given, t = \(\frac{1}{3}\)
Substituting a = 3 and t = \(\frac{1}{3}\) in (i), we get
x = 3(\(\frac{1}{3}\))2 and y = 2(3)(\(\frac{1}{3}\))
x = \(\frac{1}{3}\) and y = 2
The co-ordinates of the point on the parabola are (\(\frac{1}{3}\), 2)
∴ Focal distance = x + a
= \(\frac{1}{3}\) + 3
= \(\frac{10}{3}\)
(ii) Given equation of the parabola is 2y2 = 7x.
⇒ y2 = \(\frac{7}{2}\)x
Comparing this equation with y2 = 4ax, we get
⇒ 4a = \(\frac{7}{2}\)
⇒ a = \(\frac{7}{8}\)
If t is the parameter of the point P on the parabola, then
P(t) = (at2, 2at)
i.e., x = at2 and y = 2at …..(i)
Given, t = -2
Substituting a = \(\frac{7}{8}\) and t = -2 in (i), we get
x = \(\frac{7}{8}\)(-2)2 and y = 2(\(\frac{7}{8}\))(-2)
x = \(\frac{7}{2}\) and y = \(\frac{-7}{2}\)
The co-ordinates of the point on the parabola are (\(\frac{7}{2}\), \(\frac{-7}{2}\))
∴ Focal distance = x + a
= \(\frac{7}{2}\) + \(\frac{7}{8}\)
= \(\frac{35}{8}\)
![]()
Question 9.
For the parabola y2 = 4x, find the coordinates of the point whose focal distance is 17.
Solution:
Given the equation of the parabola is y2 = 4x.
Comparing this equation with y2 = 4ax, we get
⇒ 4a = 4
⇒ a = 1
Focal distance of a point = x + a
Given, focal distance = 17
⇒ x + 1 = 17
⇒ x = 16
Substituting x = 16 in y2 = 4x, we get
⇒ y2 = 4(16)
⇒ y2 = 64
⇒ y = ±8
∴ The co-ordinates of the point on the parabola are (16, 8) or (16, -8).
Question 10.
Find the length of the latus rectum of the parabola y2 = 4ax passing through the point (2, -6).
Solution:
Given equation of the parabola is y2 = 4ax and it passes through point (2, -6).
Substituting x = 2 and y = -6 in y2 = 4ax, we get
⇒ (-6)2 = 4a(2)
⇒ 4a = 18
∴ Length of latus rectum = 4a = 18 units
Question 11.
Find the area of the triangle formed by the line joining the vertex of the parabola x2 = 12y to the endpoints of the latus rectum.
Solution:
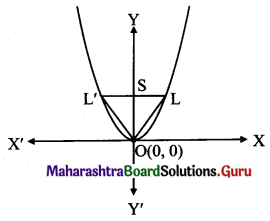
Given the equation of the parabola is x2 = 12y.
Comparing this equation with x2 = 4by, we get
⇒ 4b = 12
⇒ b = 3
The co-ordinates of focus are S(0, b), i.e., S(0, 3)
End points of the latus-rectum are L(2b, b) and L'(-2b, b),
i.e., L(6, 3) and L'(-6, 3)
Also l(LL’) = length of latus-rectum = 4b = 12
l(OS) = b = 3
Area of ∆OLL’ = \(\frac{1}{2}\) × l(LL’) × l(OS)
= \(\frac{1}{2}\) × 12 × 3
Area of ∆OLL’ = 18 sq. units
![]()
Question 12.
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find its focus.
Solution:
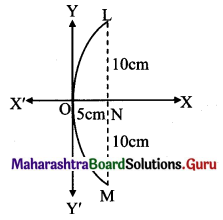
Let LOM be the parabolic reflector such that LM is the diameter and ON is its depth.
It is given that ON = 5 cm and LM = 20 cm.
LN = 10 cm
Taking O as the origin, ON along X-axis and a line through O ⊥ ON as Y-axis.
Let the equation of the reflector be y2 = 4ax ……(i)
The point L has the co-ordinates (5, 10) and lies on parabola given by (i).
Substituting x = 5 and y = 10 in (i), we get
⇒ 102 = 4a(5)
⇒ 100 = 20a
⇒ a = 5
Focus is at (a, 0), i.e., (5, 0)
Question 13.
Find co-ordinates of focus, vertex, and equation of directrix and the axis of the parabola y = x2 – 2x + 3.
Solution:
Given equation of the parabola is y = x2 – 2x + 3
⇒ y = x2 – 2x + 1 + 2
⇒ y – 2 = (x – 1)2
⇒ (x – 1)2 = y – 2
Comparing this equation with X2 = 4bY, we get
X = x – 1, Y = y – 2
⇒ 4b = 1
⇒ b = \(\frac{1}{4}\)
The co-ordinates of vertex are (X = 0, Y = 0)
⇒ x – 1 = 0 and y – 2 = 0
⇒ x = 1 and y = 2
The co-ordinates of vertex are (1, 2).
The co-ordinates of focus are S(X = 0, Y = b)
⇒ x – 1 = 0 and y – 2 = \(\frac{1}{4}\)
⇒ x = 1 and y = \(\frac{9}{4}\)
The co-ordinates of focus are (1, \(\frac{9}{4}\))
Equation of the axis is X = 0
x – 1 = 0, i.e., x = 1
Equation of directrix is Y + b = 0
⇒ y – 2 + \(\frac{1}{4}\) = 0
⇒ y – \(\frac{7}{4}\) = 0
⇒ 4y – 7 = 0
Question 14.
Find the equation of tangent to the parabola
(i) y2 = 12x from the point (2, 5)
(ii) y2 = 36x from the point (2, 9)
Solution:
(i) Given equation of the parabola is y2 = 12x.
Comparing this equation with y2 = 4ax, we get
⇒ 4a = 12
⇒ a = 3
Equation of tangent to the parabola y2 = 4ax having slope m is
y = mx + \(\frac{a}{m}\)
Since the tangent passes through the point (2, 5)
⇒ 5 = 2m + \(\frac{3}{m}\)
⇒ 5m = 2m2 + 3
⇒ 2m2 – 5m + 3 = 0
⇒ 2m2 – 2m – 3m + 3 = 0
⇒ 2m(m – 1) – 3(m – 1) = 0
⇒ (m- 1)(2m – 3) = 0
⇒ m = 1 or m = \(\frac{3}{2}\)
These are the slopes of the required tangents.
By slope point form, y – y1 = m(x – x1), the equations of the tangents are
⇒ y – 5 = 1(x – 2) and y – 5 = \(\frac{3}{2}\) (x – 2)
⇒ y – 5 = x – 2 and 2y – 10 = 3x – 6
⇒ x – y + 3 = 0 and 3x – 2y + 4 = 0
![]()
(ii) Given equation of the parabola is y2 = 36x.
Comparing this equation with y2 = 4ax, we get
⇒ 4a = 36
⇒ a = 9
Equation of tangent to the parabola y2 = 4ax having slope m is
y = mx + \(\frac{a}{m}\)
Since the tangent passes through the point (2, 9),
⇒ 9 = 2m + \(\frac{9}{m}\)
⇒ 9m = 2m2 + 9
⇒ 2m2 – 9m + 9 = 0
⇒ 2m2 – 6m – 3m + 9 = 0
⇒ 2m(m – 3) – 3(m – 3) = 0
⇒ (m – 3)(2m – 3) = 0
⇒ m = 3 or m = \(\frac{3}{2}\)
These are the slopes of the required tangents.
By slope point form, y – y1 = m(x – x1), the equations of the tangents are
⇒ y – 9 = 3(x – 2) and y – 9 = \(\frac{3}{2}\) (x – 2)
⇒ y – 9 = 3x – 6 and 2y – 18 = 3x – 6
⇒ 3x – y + 3 = 0 and 3x – 2y + 12 = 0
Question 15.
If the tangents drawn from the point (-6, 9) to the parabola y2 = kx are perpendicular to each other, find k.
Solution:
Given equation of the parabola is y2 = kx
Comparing this equation with y2 = 4ax, we get
⇒ 4a = k
⇒ a = \(\frac{\mathrm{k}}{4}\)
Equation of tangent to the parabola y2 = 4ax having slope m is
y = mx + \(\frac{a}{m}\)
Since the tangent passes through the point (-6, 9),
⇒ 9 = -6m + \(\frac{k}{4m}\)
⇒ 36m = -24m2 + k
⇒ 24m2 + 36m – k = 0
The roots m1 and m2 of this quadratic equation are the slopes of the tangents.
m1m2 = \(\frac{-\mathrm{k}}{24}\)
Since the tangents are perpendicular to each other,
m1m2 = -1
⇒ \(\frac{-\mathrm{k}}{24}\) = -1
⇒ k = 24
Alternate method:
We know that, tangents drawn from a point on directrix are perpendicular.
(-6, 9) lies on the directrix x = -a.
⇒ -6 = -a
⇒ a = 6
Since 4a = k
⇒ k = 4(6) = 24
![]()
Question 16.
Two tangents to the parabola y2 = 8x meet the tangents at the vertex in the points P and Q. If PQ = 4, prove that the equation of the locus of the point of intersection of two tangents is y2 = 8(x + 2).
Solution:
Given equation of the parabola is y2 = 8x
Comparing this equation with y2 = 4ax, we get
⇒ 4a = 8
⇒ a = 2
Equation of tangent to given parabola at A(t1) is y
t1 = x + 2\(\mathrm{t}_{1}^{2}\) …….(i)
Equation of tangent to given parabola at B(t2) is y
t2 = x + 2\(\mathrm{t}_{2}^{2}\) …..(ii)
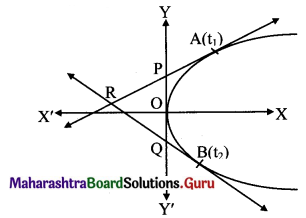
A tangent at the vertex is Y-axis whose equation is x = 0.
x-coordinate of points P and Q is 0.
Let P be(0, k1) and Q be (0, k2).
Then, from (i) and (ii), we get

∴ Equation of locus of R is y2 = 8(x + 2).
Question 17.
Find the equation of common tangent to the parabolas y2 = 4x and x2 = 32y.
Solution:
Given equation of the parabola is y2 = 4x
Comparing this equation with y2 = 4ax, we get
⇒ 4a = 4
⇒ a = 1
Let the equation of common tangent be
y = mx + \(\frac{1}{m}\) …..(i)
Substituting y = mx + \(\frac{1}{m}\) in x2 = 32y, we get
⇒ x2 = 32(mx + \(\frac{1}{m}\)) = 32 mx + \(\frac{32}{m}\)
⇒ mx2 = 32 m2x + 32
⇒ mx2 – 32 m2x – 32 = 0 ……..(ii)
Line (i) touches the parabola x2 = 32y.
The quadratic equation (ii) in x has equal roots.
Discriminant = 0
⇒ (-32m2)2 – 4(m)(-32) = 0
⇒ 1024 m4 + 128m = 0
⇒ 128m (8m3 + 1) = 0
⇒ 8m3 + 1 = 0 …..[∵ m ≠ 0]
⇒ m3 = \(-\frac{1}{8}\)
⇒ m = \(-\frac{1}{2}\)
Substituting m = \(-\frac{1}{2}\) in (i), we get
⇒ \(y=-\frac{1}{2} x+\frac{1}{\left(-\frac{1}{2}\right)}\)
⇒ \(y=-\frac{1}{2} x-2\)
⇒ x + 2y + 4 = 0, which is the equation of the common tangent.
Question 18.
Find the equation of the locus of a point, the tangents from which to the parabola y2 = 18x are such that sum of their slopes is -3.
Solution:
Given equation of the parabola is y2 = 18x
Comparing this equation with y2 = 4ax, we get
⇒ 4a = 18
⇒ a = \(\frac{9}{2}\)
Equation of tangent to the parabola y2 = 4ax having slope m is
⇒ y = mx + \(\frac{a}{m}\)
⇒ y = mx + \(\frac{9}{2m}\)
⇒ 2ym = 2xm2 + 9
⇒ 2xm2 – 2ym + 9 = 0
The roots m1 and m2 of this quadratic equation are the slopes of the tangents.
m1 + m2 = \(-\frac{(-2 y)}{2 x}=\frac{y}{x}\)
But, m1 + m2 = -3
\(\frac{y}{x}\) = -3
y = -3x, which is the required equation of locus.
![]()
Question 19.
The towers of a bridge, hung in the form of a parabola, have their tops 30 metres above the roadway and are 200 metres apart. If the cable is 5 metres above the roadway at the centre of the bridge, find the length of the vertical supporting cable 30 metres from the centre.
Solution:
Let CAB be the cable of the bridge and X’OX be the roadway.
Let A be the centre of the bridge.
From the figure, vertex of parabola is at A(0, 5).
Let the equation of parabola be
x2 = 4b(y – 5) …..(i)
Since the parabola passes through (100, 30).
Substituting x = 100 and y = 30 in (i), we get
⇒ 1002 = 4b (30 – 5)
⇒ 1002 = 4b(25)
⇒ 1002 = 100b
⇒ b = 100
Substituting the value of b in (i), we get
x2 = 400(y – 5) …..(ii)
Let l metres be the length of vertical supporting cable.
Then P(30, l) lies on (ii).
⇒ 302 = 400(l – 5)
⇒ 900 = 400(l – 5)
⇒ \(\frac{9}{4}\) = l – 5
⇒ l = \(\frac{9}{4}\) + 5
⇒ l = \(\frac{9}{4}\) m = 7.25 m
The length of the vertical supporting cable is 7.25 m.
Question 20.
A circle whose centre is (4, -1) passes through the focus of the parabola x2 + 16y = 0. Show that the circle touches the directrix of the parabola.
Solution:
Given equation of the parabola is x2 + 16y = 0.
⇒ x2 = -16y
Comparing this equation with x2 = -4by, we get
⇒ 4b = 16
⇒ b = 4
Focus = S(0, -b) = (0, -4)
Centre of the circle is C(4, -1) and it passes through focus S of the parabola.
Radius = CS
= \(\sqrt{(4-0)^{2}+(-1+4)^{2}}\)
= \(\sqrt{16+9}\)
= 5
Equation of the directrix is y – b = 0, i.e.,y – 4 = 0
Length of the perpendicular from centre C(4, -1) to the directrix
= \(\left|\frac{0(4)+1(-1)-4}{\sqrt{(0)^{2}+(1)^{2}}}\right|\)
= \(\left|\frac{-1-4}{1}\right|\)
= 5
= radius
∴ The circle touches the directrix of the parabola.