Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 7 Limits Miscellaneous Exercise 7 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 7 Limits Miscellaneous Exercise 7
I. Select the correct answer from the given alternatives.
Question 1.
\(\lim _{x \rightarrow 2}\left(\frac{x^{4}-16}{x^{2}-5 x+6}\right)=\)
(A) 23
(B) 32
(C) -32
(D) -16
Answer:
(C) -32
Hint:

Question 2.
\(\lim _{x \rightarrow-2}\left(\frac{x^{7}+128}{x^{3}+8}\right)=\)
(A) \(\frac{56}{3}\)
(B) \(\frac{112}{3}\)
(C) \(\frac{121}{3}\)
(D) \(\frac{28}{3}\)
Answer:
(B) \(\frac{112}{3}\)
Hint:

Question 3.
\(\lim _{x \rightarrow 3}\left(\frac{1}{x^{2}-11 x+24}+\frac{1}{x^{2}-x-6}\right)=\)
(A) \(-\frac{2}{25}\)
(B) \(\frac{2}{25}\)
(C) \(\frac{7}{25}\)
(D) \(-\frac{7}{25}\)
Answer:
(A) \(-\frac{2}{25}\)
Hint:

![]()
Question 4.
\(\lim _{x \rightarrow 5}\left(\frac{\sqrt{x+4}-3}{\sqrt{3 x-11-2}}\right)=\)
(A) \(\frac{-2}{9}\)
(B) \(\frac{2}{7}\)
(C) \(\frac{5}{9}\)
(D) \(\frac{2}{9}\)
Answer:
(D) \(\frac{2}{9}\)
Hint:

Question 5.
\(\lim _{x \rightarrow \frac{\pi}{3}}\left(\frac{\tan ^{2} x-3}{\sec ^{3} x-8}\right)=\)
(A) 1
(B) \(\frac{1}{2}\)
(C) \(\frac{1}{3}\)
(D) \(\frac{1}{4}\)
Answer:
(C) \(\frac{1}{3}\)
Hint:

Question 6.
\(\lim _{x \rightarrow 0}\left(\frac{5 \sin x-x \cos x}{2 \tan x-3 x^{2}}\right)=\)
(A) 0
(B) 1
(C) 2
(D) 3
Answer:
(C) 2
Hint:

Question 7.
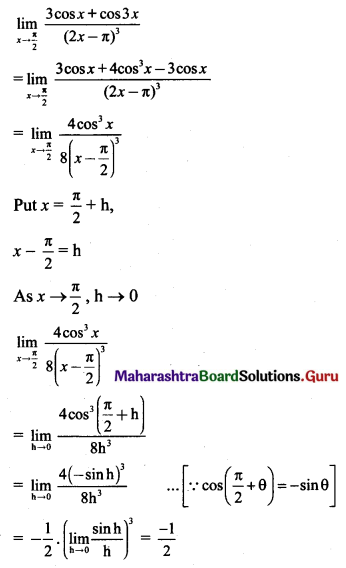
\(\lim _{x \rightarrow \frac{\pi}{2}}\left[\frac{3 \cos x+\cos 3 x}{(2 x-\pi)^{3}}\right]=\)
(A) \(\frac{3}{2}\)
(B) \(\frac{1}{2}\)
(C) \(-\frac{1}{2}\)
(D) \(\frac{1}{4}\)
Answer:
(C) \(-\frac{1}{2}\)
Hint:
Question 8.
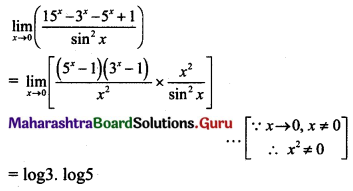
\(\lim _{x \rightarrow 0}\left(\frac{15^{x}-3^{x}-5^{x}+1}{\sin ^{2} x}\right)=\)
(A) log 15
(B) log 3 + log 5
(C) log 3 . log 5
(D) 3 log 5
Answer:
(C) log 3 . log 5
Hint:
![]()
Question 9.
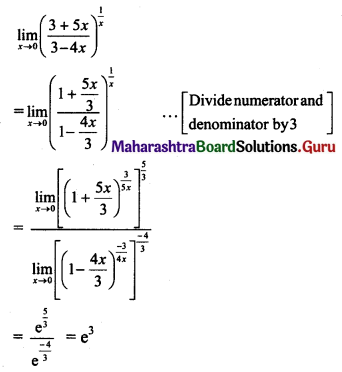
\(\lim _{x \rightarrow 0}\left(\frac{3+5 x}{3-4 x}\right)^{\frac{1}{x}}=\)
(A) e3
(B) e6
(C) e9
(D) e-3
Answer:
(A) e3
Hint:
Question 10.
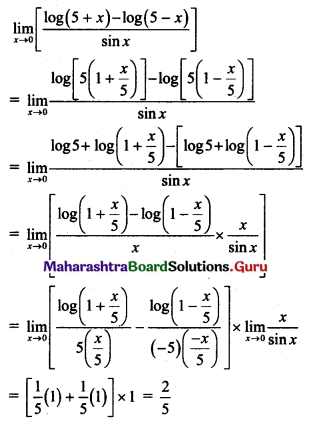
\(\lim _{x \rightarrow 0}\left[\frac{\log (5+x)-\log (5-x)}{\sin x}\right]=\)
(A) \(\frac{3}{2}\)
(B) \(-\frac{5}{2}\)
(C) \(-\frac{1}{2}\)
(D) \(\frac{2}{5}\)
Answer:
(D) \(\frac{2}{5}\)
Hint:
Question 11.
\(\lim _{x \rightarrow \frac{\pi}{2}}\left(\frac{3^{\cos x}-1}{\frac{\pi}{2}-x}\right)=\)
(A) 1
(B) log 3
(C) \(3^{\frac{\pi}{2}}\)
(D) 3 log 3
Answer:
(B) log 3
Hint:
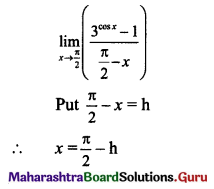
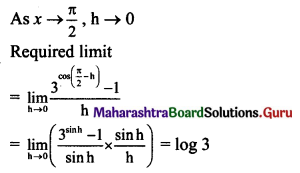
Question 12.
\(\lim _{x \rightarrow 0}\left[\frac{x \cdot \log (1+3 x)}{\left(e^{3 x}-1\right)^{2}}\right]=\)
(A) \(\frac{1}{\mathrm{e}^{9}}\)
(B) \(\frac{1}{\mathrm{e}^{3}}\)
(C) \(\frac{1}{9}\)
(D) \(\frac{1}{3}\)
Answer:
(D) \(\frac{1}{3}\)
Hint:

Question 13.
\(\lim _{x \rightarrow 0}\left[\frac{\left(3^{\sin x}-1\right)^{3}}{\left(3^{x}-1\right) \cdot \tan x \cdot \log (1+x)}\right]=\)
(A) 3 log 3
(B) 2 log 3
(C) (log 3)2
(D) (log 3)3
Answer:
(C) (log 3)2
Hint:
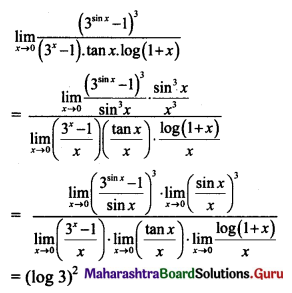
Question 14.
\(\lim _{x \rightarrow 3}\left[\frac{5^{x-3}-4^{x-3}}{\sin (x-3)}\right]=\)
(A) log 5 – 4
(B) log \(\frac{5}{4}\)
(C) \(\frac{\log 5}{\log 4}\)
(D) \(\frac{\log 5}{4}\)
Answer:
(B) log \(\frac{5}{4}\)
Hint:
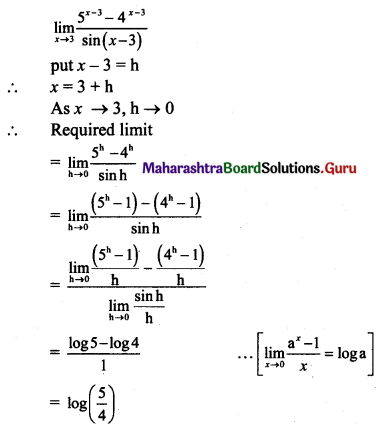
Question 15.
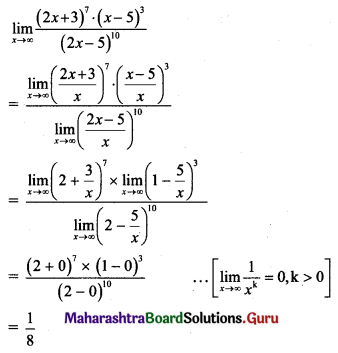
\(\lim _{x \rightarrow \infty}\left[\frac{(2 x+3)^{7}(x-5)^{3}}{(2 x-5)^{10}}\right]=\)
(A) \(\frac{3}{8}\)
(B) \(\frac{1}{8}\)
(C) \(\frac{1}{6}\)
(D) \(\frac{1}{4}\)
Answer:
(B) \(\frac{1}{8}\)
Hint:
(II) Evaluate the following.
Question 1.
\(\lim _{x \rightarrow 0}\left[\frac{(1-x)^{5}-1}{(1-x)^{3}-1}\right]\)
Solution:

Question 2.
\(\lim _{x \rightarrow 0}[x]\) ([*] is a greatest integer function.)
Solution:

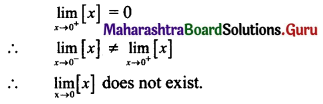
![]()
Question 3.
If f(r) = πr2 then find \(\lim _{h \rightarrow 0}\left[\frac{f(r+h)-f(r)}{h}\right]\)
Solution:

Question 4.
\(\lim _{x \rightarrow 0}\left[\frac{x}{|x|+x^{2}}\right]\)
Solution:

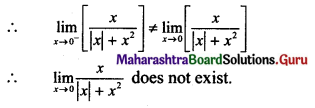
Question 5.
Find the limit of the function, if it exists, at x = 1
\(f(x)=\left\{\begin{array}{lll}
7-4 x & \text { for } & x<1 \\
x^{2}+2 & \text { for } & x \geq 1
\end{array}\right.\)
Solution:

Question 6.
Given that 7x ≤ f(x) ≤ 3x2 – 6 for all x. Determine the value of \(\lim _{x \rightarrow 3} f(x)\)
Solution:
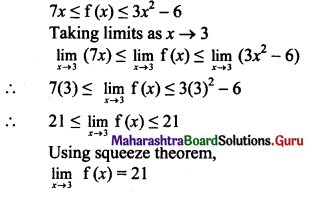
Question 7.
\(\lim _{x \rightarrow 0}\left[\frac{\sec x^{2}-1}{x^{4}}\right]\)
Solution:

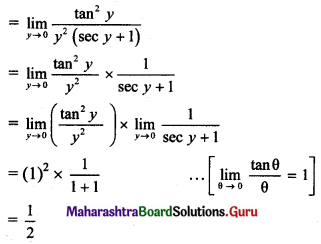
Question 8.
\(\lim _{x \rightarrow 0}\left[\frac{e^{x}+e^{-x}-2}{x \cdot \tan x}\right]\)
Solution:

Question 9.
\(\lim _{x \rightarrow 0}\left[\frac{x\left(6^{x}-3^{x}\right)}{\cos (6 x)-\cos (4 x)}\right]\)
Solution:
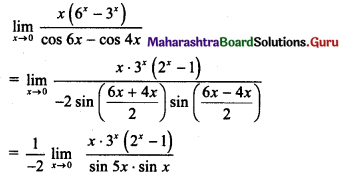

Question 10.
\(\lim _{x \rightarrow 0}\left[\frac{a^{3 x}-a^{2 x}-a^{x}+1}{x \cdot \tan x}\right]\)
Solution:

Question 11.
\(\lim _{x \rightarrow a}\left[\frac{\sin x-\sin a}{x-a}\right]\)
Solution:

![]()
Question 12.
\(\lim _{x \rightarrow 2}\left[\frac{\log x-\log 2}{x-2}\right]\)
Solution:

Question 13.
\(\lim _{x \rightarrow 1}\left[\frac{a b^{x}-a^{x} b}{x^{2}-1}\right]\)
Solution:

Question 14.
\(\lim _{x \rightarrow 0}\left[\frac{\left(5^{x}-1\right)^{2}}{\left(2^{x}-1\right) \log (1+x)}\right]\)
Solution:


Question 15.
\(\lim _{x \rightarrow \infty}\left[\frac{(2 x+1)^{2}(7 x-3)^{3}}{(5 x+2)^{5}}\right]\)
Solution:

Question 16.
\(\lim _{x \rightarrow a}\left[\frac{x \cos a-a \cos x}{x-a}\right]\)
Solution:


Question 17.
\(\lim _{x \rightarrow \frac{\pi}{4}}\left[\frac{(\sin x-\cos x)^{2}}{\sqrt{2}-\sin x-\cos x}\right]\)
Solution:

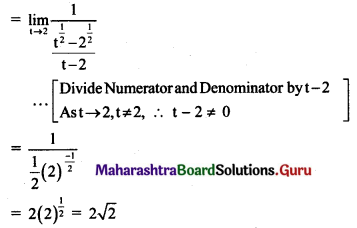
Question 18.
\(\lim _{x \rightarrow 1}\left[\frac{2^{2 x-2}-2^{x}+1}{\sin ^{2}(x-1)}\right]\)
Solution:
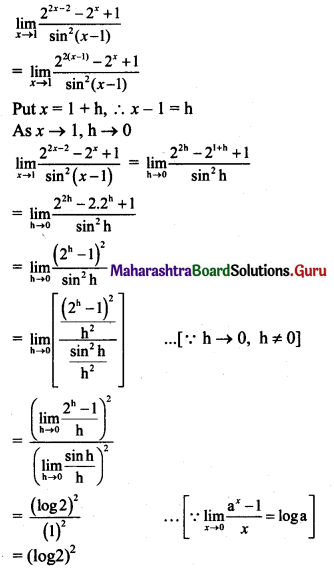
Question 19.
\(\lim _{x \rightarrow 1}\left[\frac{4^{x-1}-2^{x}+1}{(x-1)^{2}}\right]\)
Solution:


![]()
Question 20.
\(\lim _{x \rightarrow 1}\left[\frac{\sqrt{x}-1}{\log x}\right]\)
Solution:

Question 21.
\(\lim _{x \rightarrow 0}\left(\frac{\sqrt{1-\cos x}}{x}\right)\)
Solution:
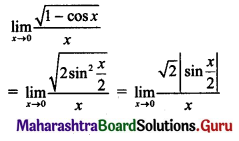

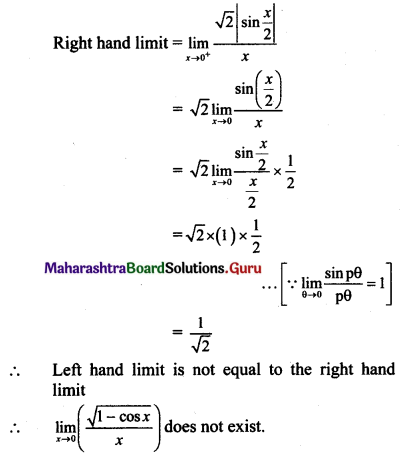
Question 22.
\(\lim _{x \rightarrow 1}\left(\frac{x+3 x^{2}+5 x^{3}+\cdots \cdots \cdots \cdots \cdots+(2 n-1) x^{n}-n^{2}}{x-1}\right)\)
Solution:



Question 23.
\(\lim _{x \rightarrow 0} \frac{1}{x^{12}}\left[1-\cos \left(\frac{x^{2}}{2}\right)-\cos \left(\frac{x^{4}}{4}\right)+\cos \left(\frac{x^{2}}{2}\right) \cdot \cos \left(\frac{x^{4}}{4}\right)\right]\)
Solution:
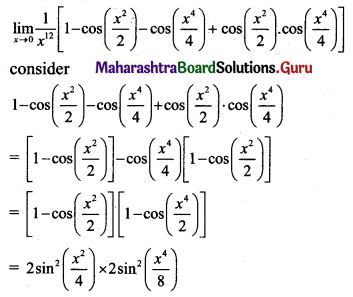
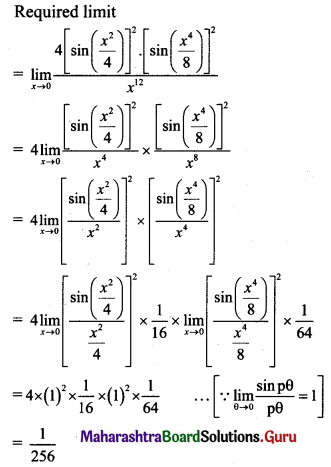
![]()
Question 24.
\(\lim _{x \rightarrow \infty}\left(\frac{8 x^{2}+5 x+3}{2 x^{2}-7 x-5}\right)^{\frac{4 x+3}{8 x-1}}\)
Solution:

