Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 9 Probability Ex 9.4 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 9 Probability Ex 9.4
Question 1.
There are three bags, each containing 100 marbles. Bag 1 has 75 red and 25 blue marbles. Bag 2 has 60 red and 40 blue marbles and Bag 3 has 45 red and 55 blue marbles. One of the bags is chosen at random and marble is picked from the chosen bag. What is the probability that the chosen marble is red?
Solution:
Let event R: Chosen marble is red.
Let event Bi: ith bag is chosen.
∴ P(Bi) = \(\frac{1}{3}\)
If Bag 1 is chosen, it has 75 red and 25 blue marbles.
∴ Probability that the chosen marble is red under the condition that it is from Bag 1 = P(R/B1)
= \(\frac{{ }^{75} \mathrm{C}_{1}}{{ }^{100} \mathrm{C}_{1}}\)
= \(\frac{75}{100}\)
= 0.75
Similarly we get,
P(R/B2) = \(\frac{60}{100}\) = 0.60
P(R/B3) = \(\frac{45}{100}\) = 0.45
∴ Required probability
P(R) = P(B1) P(R/B1) + P(B2) P(R/B2) + P(B3) P(R/B3)
= \(\frac{1}{3}\)(0.75) + \(\frac{1}{3}\)(0.60) + \(\frac{1}{3}\)(0.45)
= \(\frac{1}{3}\)(1.8)
= 0.60
![]()
Question 2.
A box contains 2 blue and 3 pink balls and another box contains 4 blue and 5 pink balls. One ball is drawn at random from one of the two boxes and it is found to be pink. Find the probability that it was drawn from
(i) first box
(ii) second box
Solution:
Let event A1: The ball is drawn from 1st box and
event A2: The ball is drawn from the 2nd box.
∴ P(A1) = \(\frac{1}{2}\), P(A2) = \(\frac{1}{2}\)
Let event B: The ball drawn is pink.
There are 5 balls in the 1st box, of which 3 are pink.
∴ P(B/A1) = \(\frac{3}{5}\)
There are 9 balls in the 2nd box, of which 5 are pink.
∴ P(B/A2) = \(\frac{5}{9}\)
(i) By Bayes’ theorem,
the probability that a pink ball is drawn from the first box, is given by
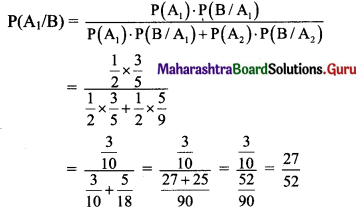
(ii) By Bayes’ theorem,
the probability that a pink ball is drawn from the second box, is given by

Question 3.
There is a working women’s hostel in a town, where 75% are from neighbouring town. The rest all are from the same town. 48% of women who hail from the same town are graduates and 83% of the women who have come from the neighbouring town are also graduates. Find the probability that a woman selected at random is a graduate from the same town.
Solution:
Let the total number of women be 100.
∴ n(S) = 100
Let event N: Women are from neighbouring town,
event W: Women are from same town and
event G: Women are graduates.
Number of women from neighbouring town,
n(N) = 75
Number of women from same town,
n(W) = 25
∴ P(N) = \(\frac{n(N)}{n(S)}=\frac{75}{100}\) and
P(W) = \(\frac{n(W)}{n(S)}=\frac{25}{100}\)
P(G/N), P(G/W) represent probabilities that woman is graduate given that she is from neighbouring town or same town respectively.
∴ P(G/N) = \(\frac{\mathrm{n}(\mathrm{G} / \mathrm{N})}{\mathrm{n}(\mathrm{S})}=\frac{83}{100}\) and
P(G/W) = \(\frac{\mathrm{n}(\mathrm{G} / \mathrm{W})}{\mathrm{n}(\mathrm{S})}=\frac{48}{100}\)
By Bayes’ theorem, the probability that a women selected at random is a graduate from the same town, is given by
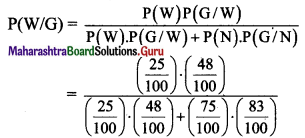

![]()
Question 4.
If E1 and E2 are equally likely, mutually exclusive and exhaustive events and P(A/E1) = 0.2, P(A/E2) = 0.3. Find P(E1/A).
Solution:
E1 and E2 are equally likely, mutually exclusive and exhaustive events.
∴ P(E1) = P(E2) = \(\frac{1}{2}\)

Question 5.
Jar I contains 5 white and 7 black balls. Jar II contains 3 white and 12 black balls. A fair coin is flipped; if it is Head, a ball is drawn from Jar I, and if it is Tail, a ball is drawn from Jar II. Suppose that this experiment is done and a white ball was drawn. What is the probability that this ball was in fact taken from Jar II?
Solution:
Let event J1: Ball drawn from jar I,
event J2: Ball drawn from jar II.
P(J1) = P(head) = \(\frac{1}{2}\)
P(J2) = P(tail) = \(\frac{1}{2}\)
Let event W: Ball drawn is white.
In Jar I, there are total 12 balls, out of which 5 balls are white.
∴ Probability that the ball drawn is white under the condtion that it is drawn from Jar I.
P(W/J1) = \(\frac{{ }^{5} C_{1}}{{ }^{12} C_{1}}=\frac{5}{12}\)
Similarly, P(W/J2) = \(\frac{{ }^{3} C_{1}}{{ }^{15} C_{1}}=\frac{3}{15}=\frac{1}{5}\)
Required probability = P(J2/W)
By Bayes’ theorem,
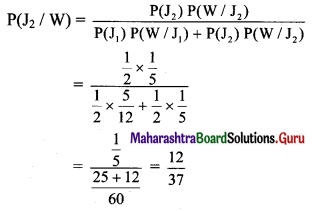
Question 6.
A diagnostic test has a probability 0.95 of giving a positive result when applied to a person suffering from a certain disease, and a probability 0.10 of giving a (false) positive result when applied to a non-sufferer. It is estimated that 0.5% of the population are sufferers. Suppose that the test is now administered to a person about whom we have no relevant information relating to the disease (apart from the fact that he/she comes from this population). Calculate the probability that:
(i) given a positive result, the person is a sufferer.
(ii) given a negative result, the person is a non-sufferer.
Solution:
Let event T: Test positive
event S: Sufferer
P(S) = \(\frac{0.5}{100}\) = 0.005
∴ P(S’) = 1 – P(S) = 1 – 0.005 = 0.995
Since a probability of getting a positive result when applied to a person suffering from a disease is 0.95 and probability of getting positive result when applied to a non sufferer is 0.10.
∴ P(T/S) = 0.95 and P(T/S’) = 0.10
∴ P(T) = P(S) P(T/S) + P(S’) P(T/S’)
= 0.005 × 0.95 + 0.995 × 0.10
= 0.10425
∴ P(T’) = 1 – P(T) = 1 – 0.10425 = 0.8958
(i) Required probability = P(S/T)
By Bayes’ theorem,

(ii) P(T’/S’) = 1 – 0.1 = 0.9
Required probability = P(S’/T’)
By Bayes’ theorem

![]()
Question 7.
A doctor is called to see a sick child. The doctor has prior information that 80% of the sick children in that area have the flu, while the other 20% are sick with measles. Assume that there is no other disease in that area. A well-known symptom of measles is rash. From the past records, it is known that, chances of having rashes given that sick child is suffering from measles is 0.95. However occasionally children with flu also develop rash, whose chance are 0.08. Upon examining the child, the doctor finds a rash. What is the probability that child is suffering from measles?
Solution:
Let the total number of sick children be 100.
∴ n(S) = 100.
Let event A: The child is sick with flu,
event B: The child is sick with measles,
event C: The child is sick with rash.
∴ n(A) = 80 and n(B) = 20
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{80}{100}=\frac{4}{5}\)
P(B) = \(\frac{n(B)}{n(S)}=\frac{20}{100}=\frac{1}{5}\)
Since the chances of having rashes, if the child is suffering from measles is 0.95 and the chances of having rashes if the child has flu is 0.08,
P(C/B) = 0.95 = \(\frac{95}{100}\) and
P(C/A) = 0.08 = \(\frac{8}{100}\)
Required probability = P(B/C)
By Bayes’ theorem,
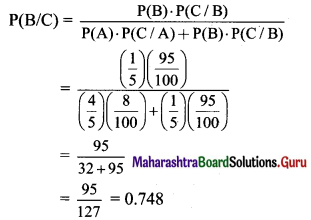
Question 8.
2% of the population have a certain blood disease of a serious form: 10% have it in a mild form; and 88% don’t have it at all. A new blood test is developed; the probability of testing positive is \(\frac{9}{10}\) if the subject has the
serious form, \(\frac{6}{10}\) if the subject has the mild form, and \(\frac{1}{10}\) if the subject doesn’t have the disease. A subject is tested positive. What is the probability that the subject has serious form of the disease?
Solution:
Let event A1: Disease in serious form,
event A2: Disease in mild form,
event A3: Subject does not have disease,
event B: Subject tests positive.
P(A1) = 0.02, P(A2) = 0.1, P(A3) = 0.88
The probability of testing positive is \(\frac{9}{10}\) if the subject has the serious form, \(\frac{6}{10}\) if the subject has the mild form, and \(\frac{1}{10}\) if the subject doesn’t have the disease.
∴ P(B/A1) = 0.9, P(B/A2) = 0.6, P(B/A3) = 0.1
P(B) = P(A1) P(B/A1) + P(A2) P(B/A2) + P(A3) P(B/A3)
= 0.02 × 0.9 + 0.1 × 0.6 + 0.88 × 0.1
= 0.166
Required probability = P(A1/B)
By Baye’s theorem

Question 9.
A box contains three coins: two fair coins and one fake two-headed coin. A coin is picked randomly from the box and tossed.
(i) What is the probability that it lands head up?
(ii) If happens to be head, what is the probability that it is the two-headed coin?
Solution:
Let event A: Fair coin is tossed,
event B: Fake coin is tossed
and event H: Head occur.
Clearly, a fair coin has one head.
∴ Probability that head occur under the condition that the fair coin is tossed = P(H/A) = \(\frac{1}{2}\)
Fake coin has two heads.
∴ Probability that head occur under the condition that the fake coin is tossed = P(H/B) = 1
n(A) = 2, n(B) = 1, n(S) = 3
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{2}{3}\)
P(B) = \(\frac{n(B)}{n(S)}=\frac{1}{3}\)
(i) Required probability
P(H) = P(A) P(H/A) + P(B) P(H/B)
= \(\frac{2}{3} \times \frac{1}{2}+\frac{1}{3} \times 1\)
= \(\frac{1}{3}+\frac{1}{3}\)
= \(\frac{2}{3}\)
![]()
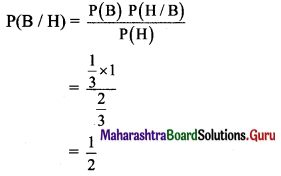
(ii) Required probability = P(B/H)
By Baye’s theorem
Question 10.
There are three social media groups on a mobile: Group I, Group II and Group III. The probabilities that Group I, Group II and Group III sending the messages on sports are \(\frac{2}{5}\), \(\frac{1}{2}\) and \(\frac{2}{3}\) respectively. The probability of opening the messages by Group I, Group II and Group III are \(\frac{1}{2}\), \(\frac{1}{4}\) and \(\frac{1}{4}\) respectively. Randomly one of the messages is opened and found a message on sports. What is the probability that the message was from Group III.
Solution:
Let event A: Message sent on sports by group I,
event B: Message sent on sports by group II,
event C: Message sent on sports by group III,
event E: Message is opened.
Given that the probabilities that Group I, Group II and Group III sending the messages on sports are \(\frac{2}{5}\), \(\frac{1}{2}\) and \(\frac{2}{3}\) respectively and the probability of opening the messages by Group I, Group II and Group III are \(\frac{1}{2}\), \(\frac{1}{4}\) and \(\frac{1}{4}\) respectively.
∴ P(A) = \(\frac{2}{5}\)
P(B) = \(\frac{1}{2}\)
P(C) = \(\frac{2}{3}\)
P(E/A) = \(\frac{1}{2}\)
P(E/B) = \(\frac{1}{4}\)
P(E/C) = \(\frac{1}{4}\)
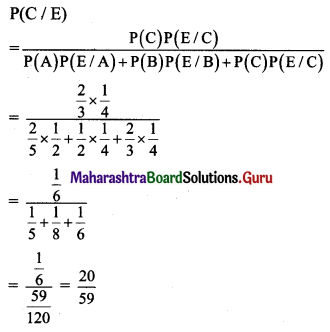
Required probability = P(C/E)
By Baye’s theorem
![]()
Question 11.
Mr. X goes to office by Auto, Car and train. The probabilities of him travelling by these modes are \(\frac{2}{7}\), \(\frac{3}{7}\), \(\frac{2}{7}\) respectively. The chances of him being late to the office are \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{4}\) respectively by Auto, Car and train. On one particular day he was late to the office. Find the probability that he travelled by car.
Solution:
Let A, C and T be the events that Mr. X goes to office by Auto, Car and Train respectively.
Let L be event that he is late.
