Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Ex 5.1 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Integration Ex 5.1
Question 1.
Evaluate \(\int \frac{-2}{\sqrt{5 x-4}-\sqrt{5 x-2}} d x\)
Solution:
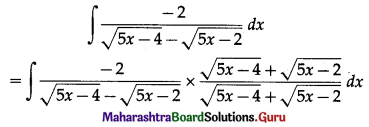

Question 2.
Evaluate \(\int\left(1+x+\frac{x^{2}}{2 !}\right) d x\)
Solution:

![]()
Question 3.
Evaluate \(\int \frac{3 x^{3}-2 \sqrt{x}}{x} d x\)
Solution:

Question 4.
Evaluate ∫(3x2 – 5)2 dx
Solution:
∫(3x2 – 5)2 dx
= ∫(9x4 – 30x2 + 25) dx
= 9∫x4 dx – 30∫x2 dx + 25∫1 dx
= 9(\(\frac{x^{5}}{5}\)) – 30(\(\frac{x^{3}}{3}\)) + 25x + c
= \(\frac{9x^{5}}{5}\) – 10x3 + 25x + c.
Question 5.
Evaluate \(\int \frac{1}{x(x-1)} d x\)
Solution:
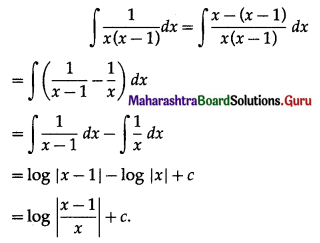
![]()
Question 6.
If f'(x) = x2 + 5 and f(0) = -1, then find the value of f(x).
Solution:
By the definition of integral
f(x) = ∫f'(x) dx
= ∫(x2 + 5) dx
= ∫x2 dx + 5∫1 dx
= \(\frac{x^{3}}{3}\) + 5x + c
Now, f(0) = -1 gives
f(0) = 0 + 0 + c = -1
∴ c = -1
∴ from (1), f(x) = \(\frac{x^{3}}{3}\) + 5x – 1.
Question 7.
If f(x) = 4x3 – 3x2 + 2x + k, f(0) = -1 and f(1) = 4, find f(x).
Solution:
By the definition of integral
f(x) = ∫f'(x) dx
= ∫(4x3 – 3x2 + 2x + k) dx
= 4∫x3 dx – 3∫x2 dx + 2∫x dx + k∫1 dx
= 4(\(\frac{x^{4}}{4}\)) – 3(\(\frac{x^{3}}{3}\)) + 2(\(\frac{x^{2}}{2}\)) + kx + c
∴ f(x) = x4 – x3 + x2 + kx + c
Now, f(0) = 1 gives
f(0) = 0 – 0 + 0 + 0 + c = 1
∴ c = 1
∴ from (1), f(x) = x4 – x3 + x2 + kx + 1
Further f(1) = 4 gives
f(1) = 1 – 1 + 1 + k + 1 = 4
∴ k = 2
∴ from (2), f(x) = x4 – x3 + x2 + 2x + 1.
![]()
Question 8.
If f(x) = \(\frac{x^{2}}{2}\) – kx + 1, f(0) = 2 and f(3) = 5, find f(x).
Solution:
By the definition of integral
