Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 6 Definite Integration Ex 6.1 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 6 Definite Integration Ex 6.1
Evaluate the following definite integrals:
Question 1.
\(\int_{4}^{9} \frac{1}{\sqrt{x}} d x\)
Solution:

Question 2.
\(\int_{-2}^{3} \frac{1}{x+5} d x\)
Solution:

![]()
Question 3.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\)
Solution:
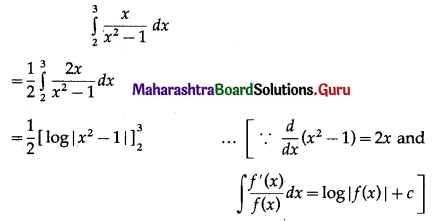
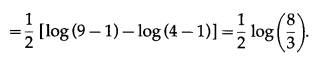
Question 4.
\(\int_{0}^{1} \frac{x^{2}+3 x+2}{\sqrt{x}} d x\)
Solution:

Question 5.
\(\int_{2}^{3} \frac{x}{(x+2)(x+3)} d x\)
Solution:
Let I = \(\int_{2}^{3} \frac{x}{(x+2)(x+3)} d x\)
Let \(\frac{x}{(x+2)(x+3)}=\frac{A}{x+3}+\frac{B}{x+2}\)
∴ x = A(x + 2) + B(x + 3)
Put x + 3 = 0, i.e. x = -3, we get
-3 = A(-1) + B(0)
∴ A = 3
Put x + 2 = 0, i.e. x = -2, we get
-2 = A(0) + B(1)
∴ B = -2
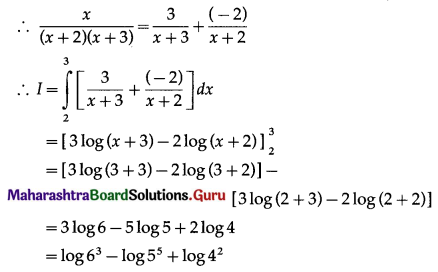
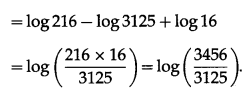
![]()
Question 6.
\(\int_{1}^{2} \frac{d x}{x^{2}+6 x+5}\)
Solution:

Question 7.
If \(\int_{0}^{a}(2 x+1) d x\) = 2, find the real values of ‘a’.
Solution:
Let I = \(\int_{0}^{a}(2 x+1) d x\)
= \(\left[2 \cdot \frac{x^{2}}{2}+x\right]_{0}^{a}\)
= a2 + a – 0
= a2 + a
∴ I = 2 gives a2 + a = 2
∴ a2 + a – 2 = 0
∴ (a + 2)(a – 1) = 0 1
∴ a + 2 = 0 or a – 1 = 0
∴ a = -2 or a = 1.
Question 8.
If \(\int_{1}^{a}\left(3 x^{2}+2 x+1\right) d x\) = 11, find ‘a’.
Solution:
Let I = \(\int_{1}^{a}\left(3 x^{2}+2 x+1\right) d x\)
= \(\left[3\left(\frac{x^{3}}{3}\right)+2\left(\frac{x^{2}}{2}\right)+x\right]_{1}^{a}\)
= \(\left[x^{3}+x^{2}+x\right]_{1}^{a}\)
= (a3 + a2 + a) – (1 + 1 + 1)
= a3 + a2 + a – 3
∴ I = 11 gives a3 + a2 + a – 3 = 11
∴ a3 + a2 + a – 14 = 0
∴ (a3 – 8) + (a2 + a – 6) = 0
∴ (a – 2)(a2 + 2a + 4) + (a + 3)(a – 2) = 0
∴ (a – 2)(a2 + 2a + 4 + a + 3) = 0
∴ (a – 2)(a2 + 3a + 7) = 0
∴ a – 2 = 0 or a2 + 3a + 7 = 0
∴ a = 2 or a = \(\frac{-3 \pm \sqrt{9-28}}{2}\)
The latter two roots are not real.
∴ they are rejected.
∴ a = 2.
![]()
Question 9.
\(\int_{0}^{1} \frac{1}{\sqrt{1+x}+\sqrt{x}} d x\)
Solution:

Question 10.
\(\int_{1}^{2} \frac{3 x}{9 x^{2}-1} d x\)
Solution:
Let I = \(\int_{1}^{2} \frac{3 x}{9 x^{2}-1} d x\) = \(\int_{1}^{2} \frac{3 x}{(3 x)^{2}-1} d x\)
Put 3x = t
∴ 3 dx = dt
∴ dx = \(\frac{d t}{3}\)
When x = 1, t = 3 × 1 = 3
When x = 2, t = 3 × 2 = 6


![]()
Question 11.
\(\int_{1}^{3} \log x d x\)
Solution:
