Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 6 Linear Programming Ex 6.1 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 6 Linear Programming Ex 6.1
Question 1.
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to a machine shop for finishing. The number of man-hours of labour required in each shop for production of A and B and the number of man-hours available for the firm is as follows.
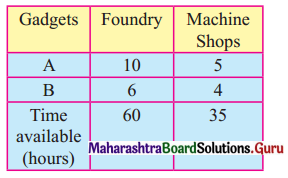
Profit on the sale of A is ₹ 30 and B ₹ 20 Per unit Formulate the LPP to have maximum profit.
Solution:
Let the manufacturing firm produce x gadgets of type A and y gadgets of type B.
On selling x gadgets of type A the firm gets ₹ 30 and that on type B is ₹ 20.
∴ Total profit is z = ₹ 30x + 20y.
Since x and y are the numbers of gadgets, x ≥ 0, y ≥ 0
From the given table, the availability of man-hours of labour required in each shop and for the firm is given as 60 and 35.
∴ The inequation are 10x + 6y ≤ 60 and 5x + 4y ≤ 35.
Hence the given LPP can be formulated as Maximize z = 30x + 20y
Subject to 10x + 6y ≤ 60, 5x + 4y ≤ 35, x ≥ 0, y ≥ 0.
![]()
Question 2.
In a cattle breeding farm, it is prescribed that the food ratio for one animal must contain 14, 22, and 1 unit of nutrients A, B, and C respectively. Two different kinds of fodder are available. Each unit weight of these two contains the following:
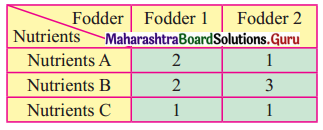
The cost of fodder 1 is ₹ 3 per unit and that of fodder 2 is ₹ 2 per unit. Formulate the LPP to minimize the cost.
Solution:
Let x unit of fodder 1 and y unit of fodder 2 be included in the ration of an animal
The cost of 1 unit of fodder 1 is ₹ 3 and the cost of 1 unit of fodder 2 is ₹ 2.
∴ The total cost is ₹ 3x + 2y.
The minimum requirement of the nutrients A, B, and C is given as 14 units, 22 units, and 1 unit.
∴ From the given table, the daily food ration will include (2x + 2y) unit of Nutrient A, (2x + 3y) unit of Nutrient B, and (x + y) of Nutrient C.
The total cost is 2 = ₹ 3x + 2y
Hence the given LPP can be formulated as Minimize z = 3x + 2y
subject to 2x + y ≥ 14, 2x + 3y ≥ 22, x + y ≥ 1, x ≥ 0, y ≥ 0.
Question 3.
A Company manufactures two types of chemicals A and B. Each chemical requires two types of raw materials P and Q. The table below shows a number of units of P and Q required to manufacture one unit of A and one unit of B.
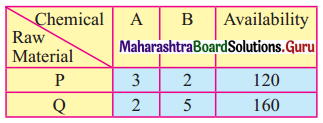
The company gets profits of ₹ 350/- and ₹ 400/- by selling one unit of A and one unit of B respectively. Formulate the problem as LPP to maximize the profit.
Solution:
∴ Let the company manufactures x unit of chemical A and y unit of chemical B.
The availability of the raw materials for the production of chemicals A and B are given as 120 and 160 units.
The company gets ₹ 350 as profit on selling one unit of chemical A and ₹ 400 as profit on selling one unit of chemical B.
∴ Total profit is ₹ (350x + 400y).
The inequation can be written as.
3x + 2y ≤ 120
2x + 5y ≤ 160
and x & y cannot be negative
Hence the LPP can be formulated as follows,
Maximize z = 350x + 400y
Subject to 3x + 2y ≤ 120, 2x + 5y ≤ 160, x ≥ 0, y ≥ 0.
![]()
Question 4.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 on magazines A and B per copy. These are processed on three machines I, II, III. Magazine A requires 2 hours on the machine I, 5 hours on machine II, and 2 hours on machine III. Magazine B requires 3 hours on machine 1, 2 hours on machine II and 6 hours on machine III. Machines I, II, III are available for 36, 50, 60 hours per week respective. Formulate the linear programming problem to maximize the profit.
Solution:
Let the company print x magazine of type A and y magazines of type B.
Then the total earnings of the company are ₹ 10x + 15y.
The given problem can be tabulated as follows.
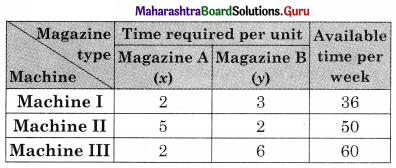
From the table, the total time required for Machine I is (2x + 3y) hours, for machine II is (5x + 2y) hours, and for machine III is (2x + 6y) hours.
The machine I, II, and III are available for 36, 50, and 60 hours per work.
∴ The constraints are 2x + 3y ≤ 36, 5x + 2y ≤ 50 and 2x + 6y ≤ 60.
Since x and y cannot be negative, we have x ≥ 0, y ≥ 0.
Hence the given LPP can be formulated as
Maximize z = 10x + 15y
Subject to 2x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60, x ≥ 0, y ≥ 0.
Question 5.
Manufacture produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on machine M1 and 3 hours of work on M2. A package of tubes requires 2 hours on machine M1 and 4 hours on machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit. He operates M1 for at most 10 hours and M2 for at most 12 hours a day.
Solution:
Let the manufacturer produce x packages of bulbs and y packages of tubes.
He earns a profit of ₹ 13.5 per packages of bulbs and ₹ 55 per package of tubes.
∴ His total profit = ₹ (13.5x + 55y).
The given problem can be tabulated as follows.
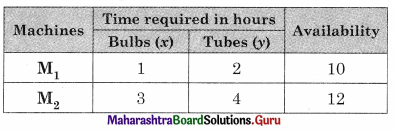
From the above table, the total time required for M1 is (x + 2y), and that of M2 is (3x + 4y).
M1 and M2 are available for at most 10 hrs per day and 12 hours per day.
∴ The constraint for the objective function is x + 2y ≤ 10, 3x + 4y ≤ 12
Hence the give LPP can be formulated as
Maximize z = 13.5x + 55y
Subject to x + 2y ≤ 10, 3x + 4y ≤ 12, x ≥ 0, y ≥ 0.
![]()
Question 6.
A Company manufactures two types of fertilizers F1 and F2. Each type of fertilizer requires two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F1 and F2 and availability of the raw materials A and B per day are given in the table below
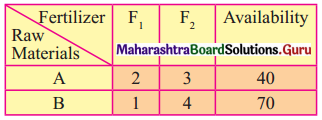
By selling one unit of F1 and one unit of F2, the company gets a profit of ₹ 500 and ₹ 750 respectively. Formulate the problem as LPP to maximize the profit.
Solution:
Let the company manufacture x units of Fertilizers F1 and y units of fertilizer F2.
The company gets a profit of ₹ 500 and ₹ 750 by selling a unit of F1 and F2.
∴ Total profit = ₹ (500x + 750y)
The availability of raw materials A and B per day is given as 40 and 70.
∴ From the given table the constraints can be written as 2x + 3y ≤ 40 and x + 4y ≤ 70.
Since x & y cannot be negative, x ≥ 0, y ≥ 0
Hence the given LPP can be formulated as
Maximize z = 500x + 750y
Subject to 2x + 3y ≤ 40, x + 4y ≤ 70, x ≥ 0, y ≥ 0.
Question 7.
A doctor has prescribed two different kinds of feeds A and B to form a weekly diet for a sick person. The minimum requirement of fats, carbohydrates, and proteins are 18, 28,14 units respectively. One unit of food A has 4 units of fat, 14 units of carbohydrates, and 8 units of protein. One unit of food B has 6 units of fat, 12 units of carbohydrates and 8 units of protein. The price of food A is ₹ 4.5 per unit and that of food B is ₹ 3.5 per unit. Form the LPP so that the sick person’s diet meets the requirements at minimum cost.
Solution:
Let x unit of food A and y unit of food B be consumed by a sick person.
The cost of food A in ₹ 4.5 per unit and food B is ₹ 3.5 per unit.
∴ Total cost = ₹ (4.5x + 3.5y)
The given conditions can be tabulated as follows.
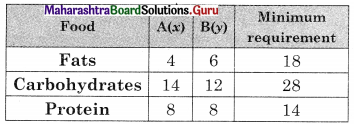
∴ The given LPP can be formulated as
Minimise z = 4.5x + 3.5y
Subject to 4x + 6y ≥ 18, 14x + 12y ≥ 28, 8x + 8y ≥ 14, x ≥ 0, y ≥ 0.
Question 8.
If John drives a car at a speed of 60 kms/hour he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 km/ hour, the cost of petrol increases to ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as LPP.
Solution:
Let John drive x km at a speed of 60 km/hr and y km at a speed of 90 km/hr.
∴ Time required to drive a distance of x km is \(\frac{x}{60}\) hours and the time require to drive at a distance of y km is \(\frac{y}{90}\) hours.
∴ Total time required \(\left(\frac{x}{60}+\frac{y}{90}\right)\) hours.
Since he wishes to drive maximum distance within an hour,
\(\frac{x}{60}+\frac{y}{90} \leq 1\)
He has to spend ₹ 5 per km at a speed of 60 km/hr and ₹ 8 per km at a speed of 90 km/hr.
He has ₹ 600 on petrol to spend, 5x + 8y ≤ 600
The total distance he wishes to travel is (x + y) hours.
∴ The given LPP can be formulated as
Maximize z = x + y
Subject to \(\frac{x}{60}+\frac{y}{90}\) ≤ 1, 5x + 8y ≤ 600, x ≥ 0, y ≥ 0.
![]()
Question 9.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg. and sand costs ₹ 6 per kg. Strength considerations dictate that a concrete brick should contain a minimum of 4 kg of cement and not more than 2 kg of sand. Formulate the LPP for the cost to be minimum.
Solution:
Let the concrete brick contain x kg of cement and y kg of sand.
The cost of cement is ₹ 20 per kg and sand is ₹ 6 per kg.
∴ The total cost = ₹ (20x + 6y)
Since the weight of the concrete brick has to be at least 5 kg, therefore, x + y ≥ 5
Also, the concrete brick should contain a minimum of 4 kg of cement, i.e. x ≥ 4, and not more than 2 kg of sand, i.e, y ≤ 2.
∴ The LPP can be formulated as
Minimize z = 20x + 6y
Subject to x + y ≥ 5, x ≥ 4, y ≤ 2, x ≥ 0, y ≥ 0.