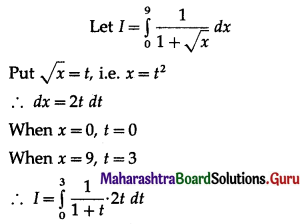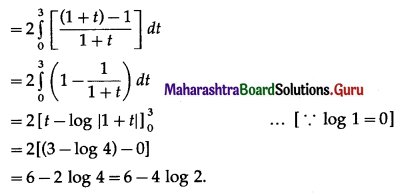Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 6 Definite Integration Miscellaneous Exercise 6 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 6 Definite Integration Miscellaneous Exercise 6
(I) Choose the correct alternative:
Question 1.
\(\int_{-9}^{9} \frac{x^{3}}{4-x^{2}} d x\) = ________
(a) 0
(b) 3
(c) 9
(d) -9
Answer:
(a) 0
Question 2.
\(\int_{-2}^{3} \frac{d x}{x+5}\) = _________
(a) -log(\(\frac{8}{3}\))
(b) log(\(\frac{8}{3}\))
(c) log(\(\frac{3}{8}\))
(d) -log(\(\frac{3}{8}\))
Answer:
(b) log(\(\frac{8}{3}\))
Question 3.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\) = _________
(a) log(\(\frac{8}{3}\))
(b) -log(\(\frac{8}{3}\))
(c) \(\frac{1}{2}\) log(\(\frac{8}{3}\))
(d) \(\frac{-1}{2}\) log(\(\frac{8}{3}\))
Answer:
(c) \(\frac{1}{2}\) log(\(\frac{8}{3}\))
![]()
Question 4.
\(\int_{4}^{9} \frac{d x}{\sqrt{x}}\) = ___________
(a) 9
(b) 4
(c) 2
(d) 0
Answer:
(c) 2
Question 5.
If \(\int_{0}^{a} 3 x^{2} d x=8\), then a = __________
(a) 2
(b) 0
(c) \(\frac{8}{3}\)
(d) a
Answer:
(a) 2
Question 6.
\(\int_{2}^{3} x^{4}\) dx = ________
(a) \(\frac{1}{2}\)
(b) \(\frac{5}{2}\)
(c) \(\frac{5}{211}\)
(d) \(\frac{211}{5}\)
Answer:
(d) \(\frac{211}{5}\)
Question 7.
\(\int_{0}^{2} e^{x}\) dx = _______
(a) e – 1
(b) 1 – e
(c) 1 – e2
(d) e2 – 1
Answer:
(d) e2 – 1
Question 8.
\(\int_{a}^{b} f(x) d x\) = ________
(a) \(\int_{b}^{a} f(x) d x\)
(b) –\(\int_{a}^{b} f(x) d x\)
(c) –\(\int_{b}^{a} f(x) d x\)
(d) \(\int_{0}^{a} f(x) d x\)
Answer:
(c) –\(\int_{b}^{a} f(x) d x\)
![]()
Question 9.
\(\int_{-7}^{7} \frac{x^{3}}{x^{2}+7} d x\) = _________
(a) 7
(b) 49
(c) 0
(d) \(\frac{7}{2}\)
Answer:
(c) 0
Question 10.
\(\int_{2}^{7} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{9-x}} d x\) = _________
(a) \(\frac{7}{2}\)
(b) \(\frac{5}{2}\)
(c) 7
(d) 2
Answer:
(b) \(\frac{5}{2}\)
(II) Fill in the blanks:
Question 1.
\(\int_{0}^{2} e^{x} d x\) = ________
Answer:
e2 – 1
Question 2.
\(\int_{2}^{3} x^{4} d x\) = __________
Answer:
\(\frac{211}{5}\)
Question 3.
\(\int_{0}^{1} \frac{d x}{2 x+5}\) = ____________
Answer:
\(\frac{1}{2} \log \left(\frac{7}{5}\right)\)
Question 4.
If \(\int_{0}^{a} 3 x^{2} d x\) = 8, then a = _________
Answer:
2
![]()
Question 5.
\(\int_{4}^{9} \frac{1}{\sqrt{x}} d x\) = _________
Answer:
2
Question 6.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\) = _________
Answer:
\(\frac{1}{2} \log \left(\frac{8}{3}\right)\)
Question 7.
\(\int_{-2}^{3} \frac{d x}{x+5}\) = _________
Answer:
\(\log \left(\frac{8}{3}\right)\)
Question 8.
\(\int_{-9}^{9} \frac{x^{3}}{4-x^{2}} d x\) = _____________
Answer:
o
(III) State whether each of the following is True or False:
Question 1.
\(\int_{a}^{b} f(x) d x=\int_{-b}^{-a} f(x) d x\)
Answer:
True
Question 2.
\(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(t) d t\)
Answer:
True
![]()
Question 3.
\(\int_{0}^{a} f(x) d x=\int_{a}^{0} f(a-x) d x\)
Answer:
False
Question 4.
\(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(x-a-b) d x\)
Answer:
False
Question 5.
\(\int_{-5}^{5} \frac{x^{3}}{x^{2}+7} d x=0\)
Answer:
True
Question 6.
\(\int_{1}^{2} \frac{\sqrt{x}}{\sqrt{3-x}+\sqrt{x}} d x=\frac{1}{2}\)
Answer:
True
Question 7.
\(\int_{2}^{7} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{9-x}} d x=\frac{9}{2}\)
Answer:
False
Question 8.
\(\int_{4}^{7} \frac{(11-x)^{2}}{(11-x)^{2}+x^{2}} d x=\frac{3}{2}\)
Answer:
True
(IV) Solve the following:
Question 1.
\(\int_{2}^{3} \frac{x}{(x+2)(x+3)} d x\)
Solution:
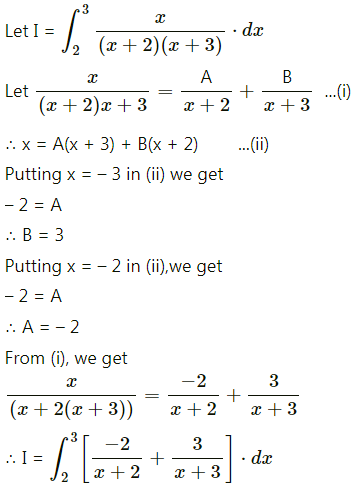
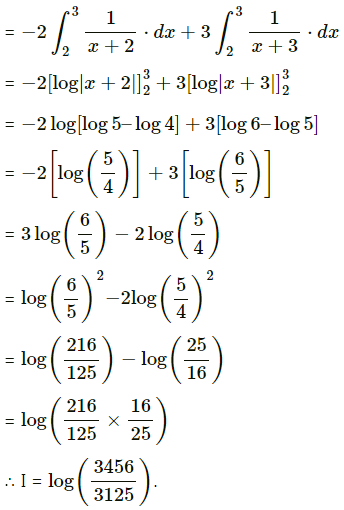
Question 2.
\(\int_{1}^{2} \frac{x+3}{x(x+2)} d x\)
Solution:
Let I = \(\int_{1}^{2} \frac{x+3}{x(x+2)} d x\)
Let \(\frac{x+3}{x(x+2)}=\frac{A}{x}+\frac{B}{x+2}\)
∴ x + 3 = A(x + 2) + Bx
Put x = 0, we get
3 = A(2) + B(0)
∴ A = \(\frac{3}{2}\)
Put x + 2 = 0, i.e. x = -2, we get
-2 + 3 = A(0) + B(-2)
∴ 1 = -2B
∴ B = \(-\frac{1}{2}\)

![]()
Question 3.
\(\int_{1}^{3} x^{2} \log x d x\)
Solution:

Question 4.
\(\int_{0}^{1} e^{x^{2}} \cdot x^{3} d x\)
Solution:
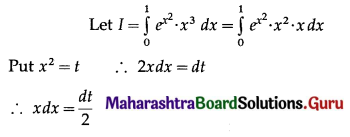

Question 5.
\(\int_{1}^{2} e^{2 x}\left(\frac{1}{x}-\frac{1}{2 x^{2}}\right) d x\)
Solution:

Question 6.
\(\int_{4}^{9} \frac{1}{\sqrt{x}} d x\)
Solution:
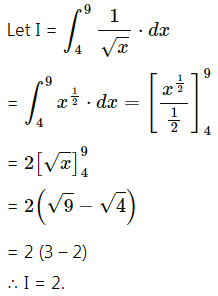
Question 7.
\(\int_{-2}^{3} \frac{1}{x+5} d x\)
Solution:
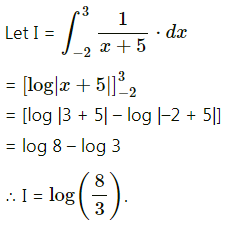
![]()
Question 8.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\)
Solution:
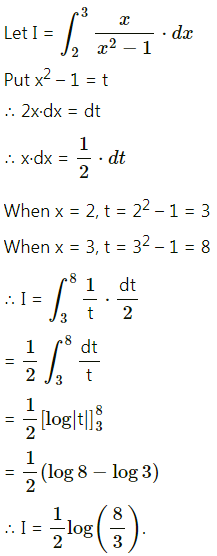
Question 9.
\(\int_{0}^{1} \frac{x^{2}+3 x+2}{\sqrt{x}} d x\)
Solution:
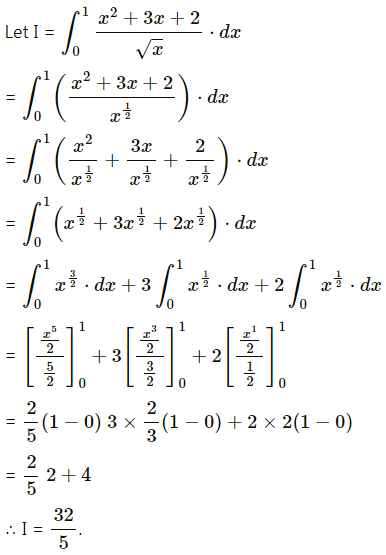
Question 10.
\(\int_{3}^{5} \frac{d x}{\sqrt{x+4}+\sqrt{x-2}}\)
Solution:

Question 11.
\(\int_{2}^{3} \frac{x}{x^{2}+1} d x\)
Solution:

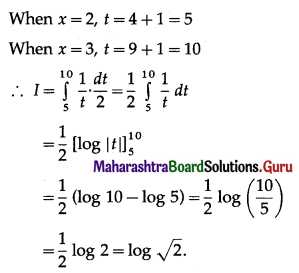
Question 12.
\(\int_{1}^{2} x^{2} d x\)
Solution:

![]()
Question 13.
\(\int_{-4}^{-1} \frac{1}{x} d x\)
Solution:
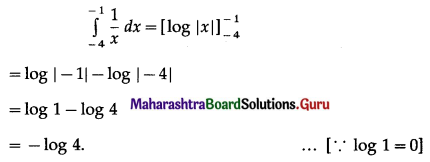
Question 14.
\(\int_{0}^{1} \frac{1}{\sqrt{1+x}+\sqrt{x}} d x\)
Solution:
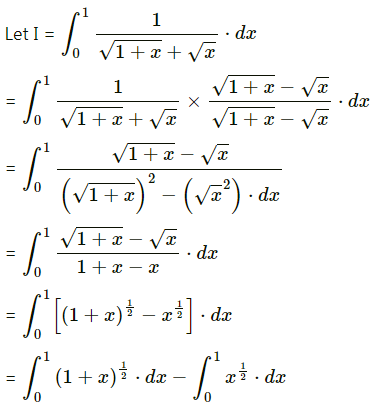
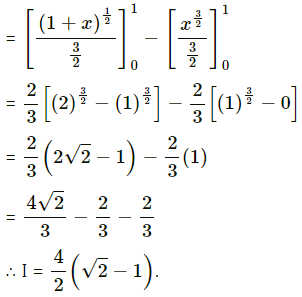
Question 15.
\(\int_{0}^{4} \frac{1}{\sqrt{x^{2}+2 x+3}} d x\)
Solution:

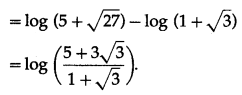
Question 16.
\(\int_{2}^{4} \frac{x}{x^{2}+1} d x\)
Solution:
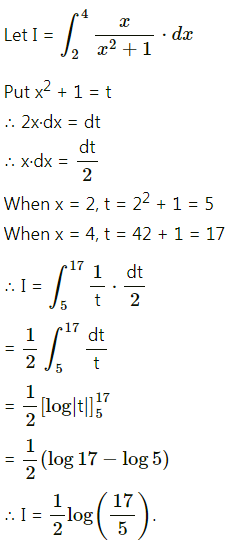
Question 17.
\(\int_{0}^{1} \frac{1}{2 x-3} d x\)
Solution:

Question 18.
\(\int_{1}^{2} \frac{5 x^{2}}{x^{2}+4 x+3} d x\)
Solution:
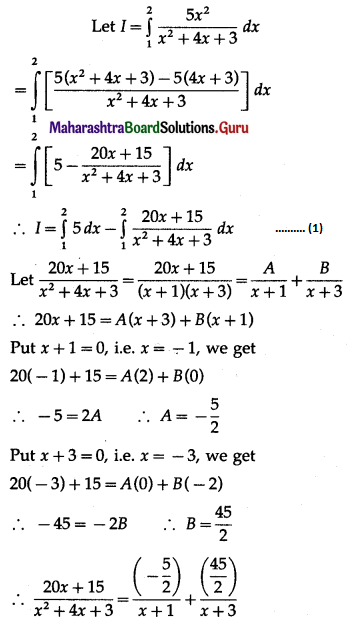
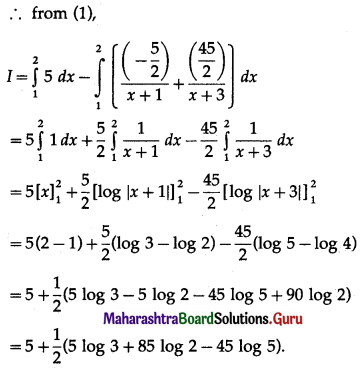
![]()
Question 19.
\(\int_{1}^{2} \frac{d x}{x(1+\log x)^{2}}\)
Solution:

Question 20.
\(\int_{0}^{9} \frac{1}{1+\sqrt{x}} d x\)
Solution: