Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.1 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.1
Question 1.
Let X represent the difference between a number of heads and the number of tails obtained when a coin is tossed 6 times. What are the possible values of X?
Solution:
∵ A coin is tossed 6 times
S = {6H and 0T, 5H and 1T, 4H and 2T, 3H and 3T, 2H and 4T, 1H and 5T, 0H and 6T}
X: Difference between no. of heads and no. of tails.
X = 6 – 0 = 6
X = 5 – 1 = 4
X = 4 – 2 = 2
X = 3 – 3 = 0
X = 2 – 4 = -2
X = 1 – 5 = -4
X = 0 – 6 = -6
X = {-6, -4, -2, 0, 2, 4, 6}
![]()
Question 2.
An urn contains 5 red and 2 black balls. Two balls are drawn at random. X denotes the number of black balls drawn. What are the possible values of X?
Solution:
S : Two bolts are drawn from the Urn
S = {RR, RB, BR, BB}
X : No. of black balls
∴ X = {0, 1, 2}
Question 3.
Determine whether each of the following is a probability distribution. Give reasons for your answer.
(i)
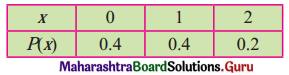
Solution:
Here, P(X = x) ≥ 0, ∀ x and
\(\sum_{x=0}^{2} \mathrm{P}(\mathrm{X}=x)\) = p(0) + p(1) + p(2)
= 0.4 + 0.4 + 0.2
= 1
∴ The function is a p.m.f.
(ii)
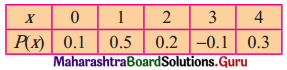
Solution:
Here, p(3) = -0.1 < 0
∴ P(X = x) ≯ 0, ∀ x
∴ The function is not a p.m.f.
(iii)
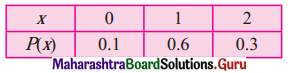
Solution:
Here, P(X = x) ≥ 0, ∀ x and
\(\sum_{x=0}^{2} \mathrm{P}(\mathrm{X}=x)\) = p(0) + p(1) + p(2)
= 0.1 + 0.6 + 0.3
= 1
∴ The function is a p.m.f.
(iv)
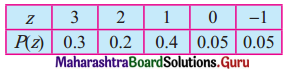
Solution:
Here, P(Z = z) ≥ 0, ∀ z and
\(\sum_{x=-1}^{3} \mathrm{P}(\mathrm{Z}=z)\) = p(-1) + p(0) + p(1) + p(2) + p(3)
= 0.05 + 0 + 0.4 + 0.2 + 0.3
= 0.95
≠ 1
∴ The function is not a p.m.f.
![]()
(v)
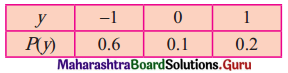
Solution:
Here, P(Y = y) ≥ 0, ∀ y and
\(\sum_{x=-1}^{2} \mathrm{P}(\mathrm{Y}=y)\) = p(-1) + p(0) + p(1)
= 0.1 + 0.6 + 0.2
= 0.9
≠ 1
∴ The function is not a p.m.f.
(vi)
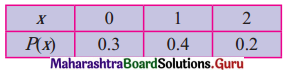
Solution:
Here, P(X = x) ≥ 0, ∀ x and
\(\sum_{x=0}^{0} \mathrm{P}(X=x)\) = p(-2) + p(-1) + p(0)
= 0.3 + 0.4 + 0.2
= 0.9
≠ 1
∴ The function is not a p.m.f.
Question 4.
Find the probability distribution of
(i) number of heads in two tosses of a coin,
(ii) number of trails in three tosses of a coin,
(iii) number of heads in four tosses of a coin.
Solution:
(i) S: Coin is tossed two times
S = {HH, HT, TH, TT}
n(S) = 4
X: No. of heads
Range of X = {0, 1, 2}
p.m.f. Table
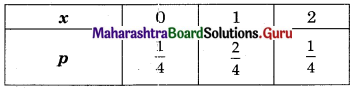
(ii) S: 3 coin are tossed
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
X: No. of heads
Range of X = {0, 1, 2, 3}
p.m.f. Table
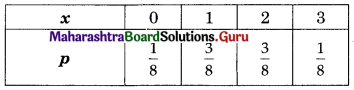
(iii) S: Four coin are tossed
S = {HHHH, HHHT, HHTH, HHTT, HTHH, HTHT, HTTH, HTTT, THHH, THHT, THTH, THTT, TTHH, TTHT, TTTH, TTTT}
n(S) = 16
X: No. of heads
Range of X = {0, 1, 2, 3, 4}
p.m.f. Table
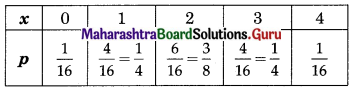
Question 5.
Find the probability distribution of the number of successes in two tosses of a die if successes are defined as getting a number greater than 4.
Solution:
S = A die is tossed 2 times
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
X = No. getting greater than 4
Range of X = {0, 1, 2}
p(0) = \(\frac{16}{36}=\frac{4}{9}\)
p(1) = \(\frac{16}{36}=\frac{4}{9}\)
p(2) = \(\frac{4}{36}=\frac{1}{9}\)

Question 6.
A sample of 4 bulbs is drawn at random with replacement from a lot of 30 bulbs which includes 6 defective bulbs. Find the probability distribution of the number of defective bulbs.
Solution:
Total no. of bulbs = 30
No. of defective bulbs = 6
A sample of 4 bulbs are drawn from 30 bulbs.
∴ n(S) = \({ }^{30} \mathrm{C}_{4}\)
∴ No. of non-defective bulbs = 24
Let X = No. of defective bulbs drawn in sample of 4 bulbs.


![]()
Question 7.
A coin is biased so that the head is 3 times as likely to occur as the tail. Find the probability distribution of a number of tails in two tosses.
Solution:
Here, the head is 3 times as likely to occur as the tail.
i.e., If 4 times coin is tossed, 3 times there will be a head and 1 time there will be the tail.
∴ p(H) = \(\frac{3}{4}\) and p(T) = \(\frac{1}{4}\)
Let X : No. of tails in two tosses.
And coin is tossed twice.
∴ X = {0, 1, 2}
For X = 0,
p(0) = p(both heads)
= p(H) × p(H)
= \(\frac{3}{4} \times \frac{3}{4}\)
= \(\frac{9}{16}\)
For X = 1,
p(1) = p(HT or TH)
= p(HT) + p(TH)
= p(H) × p(T) + p(T) × p(H)
= \(\frac{3}{4} \times \frac{1}{4}+\frac{1}{4} \times \frac{3}{4}\)
= \(\frac{6}{16}\)
For X = 2,
p(2) = p(both tails)
= p(T) × p(T)
= \(\frac{1}{4} \times \frac{1}{4}\)
= \(\frac{1}{16}\)
The probability distribution of the number of tails in two tosses is

Question 8.
A random variable X has the following probability distribution:

Determine (i) k, (ii) P(X < 3), (iii) P(0 < X < 3), (iv) P(X > 4).
Solution:
(i) It is a p.m.f. of r.v. X
∴ Σp(x) = 1
∴ p(1) + p(2) + p(3) + p(4) + p(5) + p(6) + p(7) = 1
∴ k + 2k + 2k + 3k + k2 + 2k2 + (7k2 + k) = 1
∴ 10k2 + 9k = 1
∴ 10k2 + 9k – 1 = 0
∴ 10k2 + 10k – k – 1 = 0
∴ 10k(k + 1) – (k + 1) = 0
∴ (10k – 1)(k + 1) = 0
∴ 10k – 1 = 0 or k + 1 = 0
∴ k = \(\frac{1}{10}\) or k = -1
but k = -1 is not accepted
∴ k = \(\frac{1}{2}\) is accepted
(ii) P(X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)
(iii) P(0 < X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)
(iv) P(X > 4) = p(5) + p(6) + p(7)
= k2 + 2k2 + (7k2 + k)
= 10k2 + k
= \(10\left(\frac{1}{10}\right)^{2}+\frac{1}{10}\)
= \(\frac{2}{10}\)
= \(\frac{1}{5}\)
Question 9.
Find expected value and variance of X using the following p.m.f.
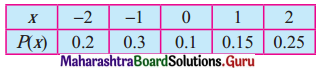
Solution:
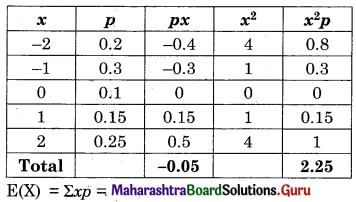
E(X) = Σxp = -0.05
V(X) = Σx2p – (Σxp)2
= 2.25 – (-0.05)2
= 2.25 – 0.0025
= 2.2475
Question 10.
Find expected value and variance of X, the number on the uppermost face of a fair die.
Solution:
S : A fair die is thrown
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
X: No obtained on uppermost face of die
Range of X = {1, 2, 3, 4, 5, 6}
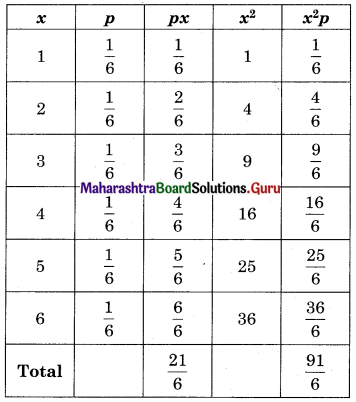
E(X) = Σxp = \(\frac{21}{6}=\frac{7}{2}\) = 3.5
V(X) = Σx2p – (Σxp)2
= \(\frac{91}{6}\) – (3.5)2
= 15.17 – 12.25
= 2.92
Question 11.
Find the mean of the number of heads in three tosses of a fair coin.
Solution:
S : A coin is tossed 3 times
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
n(S) = 8
Range of X = {0, 1, 2, 3}
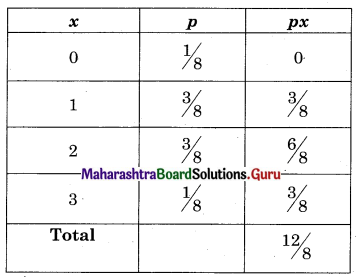
∴ Mean = E(X) = Σxp = \(\frac{12}{8}=\frac{3}{2}\) = 1.5
Question 12.
Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.
Solution:
S : Two dice are thrown
S = {(1, 1), (1, 2), (1, 3), ……, (6, 6)}
n(S) = 36
Range of X = {0, 1, 2}
First 6 positive integers are 1, 2, 3, 4, 5, 6
X = Larger two numbers selected
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
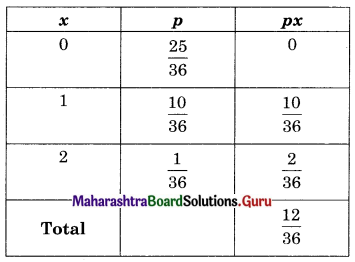
∴ E(X) = Σxp = \(\frac{12}{36}=\frac{1}{3}\)
![]()
Question 13.
Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers. Find E(X).
Solution:
First 6 positive integers are 1, 2, 3, 4, 5, 6
X : The larger of the selected two numbers
S = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
n(S) = 30
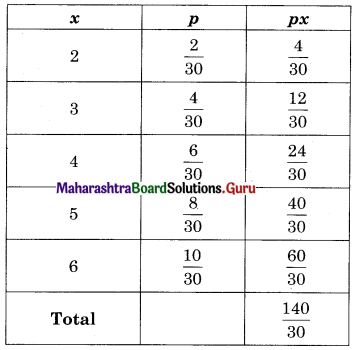
E(X) = Σxp = \(\frac{140}{30}=\frac{14}{3}\) = 4.67
Question 14.
Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance of X.
Solution:
S : Two fair dice are rolled
S = {(1, 1), (1, 2), (1, 4), ……, (6, 6)}
n(S) = 36
X : Sum of the two numbers.
Range of X = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
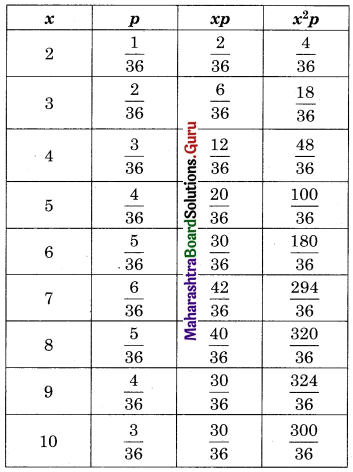
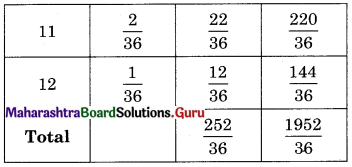
V(X) = Σx2p – (Σxp)2
= \(\frac{1952}{36}-\left(\frac{252}{36}\right)^{2}\)
= 54.22 – (7)2
= 5.22
SD(X) = √V(X) = √5.22 = 2.28
Question 15.
A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. If X denotes the age of a randomly selected student, find the probability distribution of X. Find the mean and variance of X.
Solution:
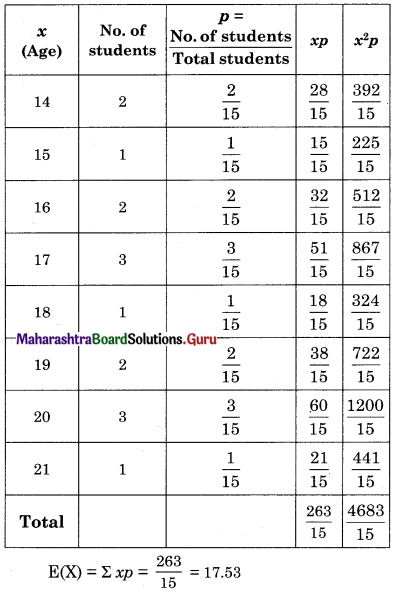

![]()
Question 16.
70% of the member’s favour and 30% oppose a proposal in a meeting. The random variable X takes the value 0 if a member opposes the proposal and the value 1 if a member is in favour. Find E(X) and V(X).
Solution:
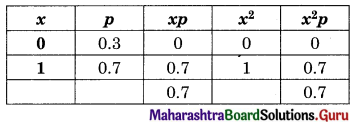
E(X) = Σxp = 0.7
V(X) = Σx2p – (Σxp)2
= 0.7 – (0.7)2
= 0.7 – 0.49
= 0.21