Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.2 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Ex 8.2
Question 1.
Obtain the differential equation by eliminating arbitrary constants from the following equations:
(i) y = Ae3x + Be-3x
Solution:
y = Ae3x + Be-3x ……(1)
Differentiating twice w.r.t. x, we get

This is the required D.E.
(ii) y = \(c_{2}+\frac{c_{1}}{x}\)
Solution:
y = \(c_{2}+\frac{c_{1}}{x}\)
∴ xy = c2x + c1
Differentiating w.r.t. x, we get

![]()
(iii) y = (c1 + c2x) ex
Solution:
y = (c1 + c2x) ex
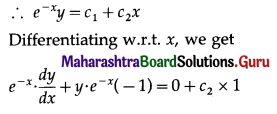

This is the required D.E.
(iv) y = c1 e3x+ c2 e2x
Solution:


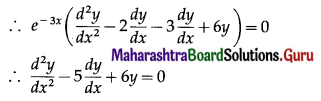
This is the required D.E.
(v) y2 = (x + c)3
Solution:
y2 = (x + c)3
Differentiating w.r.t. x, we get

This is the required D.E.
![]()
Question 2.
Find the differential equation by eliminating arbitrary constant from the relation x2 + y2 = 2ax.
Solution:
x2 + y2 = 2ax
Differentiating both sides w.r.t. x, we get
2x + 2y\(\frac{d y}{d x}\) = 2a
Substituting value of 2a in equation (1), we get
x2 + y2 = [2x + 2y \(\frac{d y}{d x}\)]x = 2x2 + 2xy \(\frac{d y}{d x}\)
∴ 2xy \(\frac{d y}{d x}\) = y2 – x2 is the required D.E.
Question 3.
Form the differential equation by eliminating arbitrary constants from the relation bx + ay = ab.
Solution:
bx + ay = ab
∴ ay = -bx + ab
∴ y = \(-\frac{b}{a} x+b\)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}=-\frac{b}{a} \times 1+0=-\frac{b}{a}\)
Differentiating again w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = 0 is the required D.E.
Question 4.
Find the differential equation whose general solution is x3 + y3 = 35ax.
Solution:
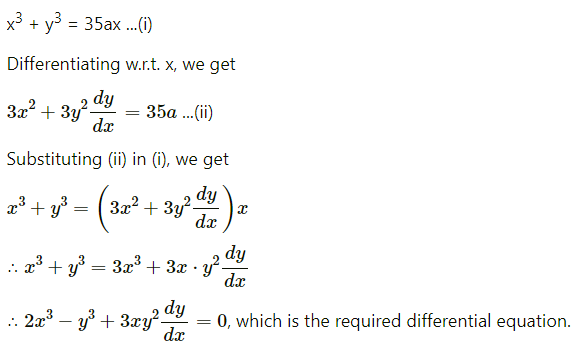
![]()
Question 5.
Form the differential equation from the relation x2 + 4y2 = 4b2.
Sol ution:
x2 + 4y2 = 4b2
Differentiating w.r.t. x, we get
2x + 4(2y\(\frac{d y}{d x}\)) = 0
i.e. x + 4y\(\frac{d y}{d x}\) = 0 is the required D.E.