Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Ex 8.4 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Ex 8.4
Question 1.
If X has Poisson distribution with m = 1, then find P(X ≤ 1) given e-1 = 0.3678.
Solution:
∵ m = 1
∵ X follows Poisson Distribution
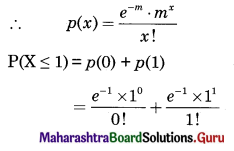
= e-m × 1 + e-m × 1
= e-1 + e-1
= 2 × e-1
= 2 × 0.3678
= 0.7356
![]()
Question 2.
If X ~ P(\(\frac{1}{2}\)), then find P(X = 3) given e-0.5 = 0.6065.
Solution:

Question 3.
If X has Poisson distribution with parameter m and P(X = 2) = P(X = 3), then find P(X ≥ 2). Use e-3 = 0.0497
Solution:
∵ X follows Poisson Distribution

Question 4.
The number of complaints which a bank manager receives per day follows a Poisson distribution with parameter m = 4. Find the probability that the manager receives (i) only two complaints on a given day, (ii) at most two complaints on a given day. Use e-4 = 0.0183.
Solution:
∵ m = 1
∵ X ~ P(m = 4)
∴ p(x) = \(\frac{e^{-m} \cdot m^{x}}{x !}\)
X = No. of complaints recieved
(i) P(Only two complaints on a given day)

(ii) P(Atmost two complaints on a given day)
P(X ≤ 2) = p(0) + p(1) + p(2)
= \(\frac{e^{-4} \times 4^{0}}{0 !}+\frac{e^{-4} \times 4^{1}}{1 !}\) + 0.1464
= e-4 + e-4 × 4 + 0.1464
= e-4 [1 + 4] + 0.1464
= 0.0183 × 5 + 0.1464
= 0.0915 + 0.1464
= 0.2379
![]()
Question 5.
A car firm has 2 cars, which are hired out day by day. The number of cars hired on a day follows a Poisson distribution with a mean of 1.5. Find the probability that
(i) no car is used on a given day.
(ii) some demand is refused on a given day, given e-1.5 = 0.2231.
Solution:
Let X = No. of demands for a car on any day
∴ No. of cars hired
n = 2
m = 1.5
∵ X ~ P(m = 1.5)

Question 6.
Defects on plywood sheets occur at random with an average of one defect per 50 sq. ft. Find the probability that such a sheet has (i) no defect, (ii) at least one defect. Use e-1 = 0.3678.
Solution:
∵ X = No. of defects on a plywood sheet
∵ m = -1
∵ X ~ P(m = -1)
∴ p(x) = \(\frac{e^{-m} \cdot m^{x}}{x !}\)
(i) P(No defect)
P(X = 0) = \(\frac{e^{-1} \times 1^{0}}{0 !}\)
= e-1
= 0.3678
(ii) P(At least one defect)
P(X ≥ 1) = 1 – P(X < 1)
= 1 – p(0)
= 1 – 0.3678
= 0.6322
![]()
Question 7.
It is known that, in a certain area of a large city, the average number of rats per bungalow is five. Assuming that the number of rats follows Poisson distribution, find the probability that a randomly selected bungalow has
(i) exactly 5 rats
(ii) more than 5 rats
(iii) between 5 and 7 rats, inclusive. Given e-5 = 0.0067.
Solution:
X = No. of rats
∵ m = 5
∴ X ~ P(m = 5)
∴ p(x) = \(\frac{e^{-m} \cdot m^{x}}{x !}\)
(i) P(Exactly five rats)

(ii) P(More than five rats)
P(X > 5) = 1 – P(X ≤ 5)

(iii) P(between 5 and 7 rats, inclusive)
P(5 ≤ x ≤ 7) = p(5) + p(6) + p(7)
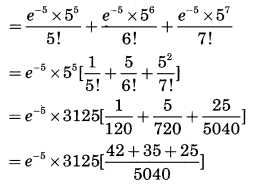
= 0.0067 × 3125 × 0.02
= 0.0067 × 62.5
= 0.42