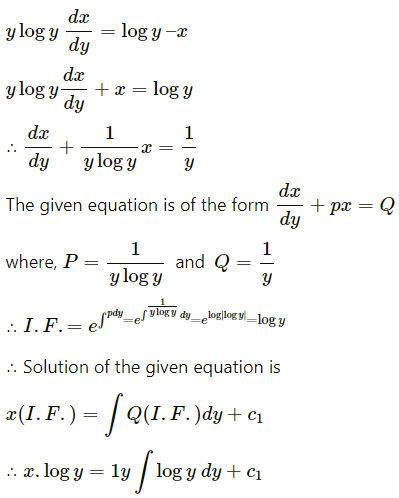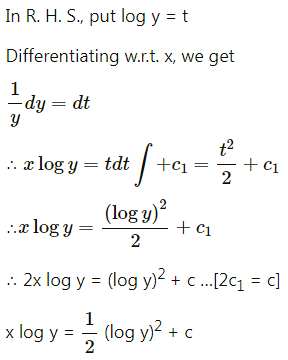Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8
(I) Choose the correct option from the given alternatives:
Question 1.
The order and degree of \(\left(\frac{d y}{d x}\right)^{3}-\frac{d^{3} y}{d x^{3}}+y e^{x}=0\) are respectively.
(a) 3, 1
(b) 1, 3
(c) 3, 3
(d) 1, 1
Answer:
(a) 3, 1
Question 2.
The order and degree of \(\left[1+\left(\frac{d y}{d x}\right)^{3}\right]^{\frac{2}{3}}=8 \frac{d^{3} y}{d x^{3}}\) are respectively
(a) 3, 1
(c) 3, 3
(b) 1, 3
(d) 1, 1
Answer:
(c) 3, 3
![]()
Question 3.
The differential equation of y = k1 + \(\frac{k_{2}}{x}\) is
(a) \(\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
(b) \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
(c) \(\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}=0\)
(d) \(x \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}=0\)
Answer:
(b) \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
Question 4.
The differential equation of y = k1 ex + k2 e-x is
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)
(b) \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)
(c) \(\frac{d^{2} y}{d x^{2}}+y \frac{d y}{d x}=0\)
(d) \(\frac{d^{2} y}{d x^{2}}+y=0\)
Answer:
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)
Question 5.
The solution of \(\frac{d y}{d x}\) = 1 is
(a) x + y = c
(b) xy = c
(c) x2 + y2 = c
(d) y – x = c
Answer:
(d) y – x = c
Question 6.
The solution of \(\frac{d y}{d x}+\frac{x^{2}}{y^{2}}=0\) is
(a) x3 + y3 = 7
(b) x2 + y2 = c
(c) x3 + y3 = c
(d) x + y = c
Answer:
(c) x3 + y3 = c
![]()
Question 7.
The solution of x \(\frac{d y}{d x}\) = y log y is
(a) y = aex
(b) y = be2x
(c) y = be-2x
(d) y = eax
Answer:
(d) y = eax
Question 8.
Bacterial increases at a rate proportional to the number present. If the original number M doubles in 3 hours, then the number of bacteria will be 4M in
(a) 4 hours
(b) 6 hours
(c) 8 hours
(d) 10 hours
Answer:
(b) 6 hours
Question 9.
The integrating factor of \(\frac{d y}{d x}\) – y = ex is
(a) x
(b) -x
(c) ex
(d) e-x
Answer:
(c) ex
![]()
Question 10.
The integrating factor of \(\frac{d y}{d x}\) – y = ex is e-x, then its solution is
(a) ye-x = x + c
(b) yex = x + c
(c) yex = 2x + c
(d) ye-x = 2x + c
Answer:
(a) ye-x = x + c
(II) Fill in the blanks:
Question 1.
The order of highest derivative occurring in the differential equation is called ________ of the differential equation.
Answer:
order
Question 2.
The power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any is called ________ of the differential equation.
Answer:
degree
Question 3.
A solution of differential equation that can be obtained from the general solution by giving particular values to the arbitrary constants is called _________ solution.
Answer:
particular
Question 4.
Order and degree of a differential equation are always _________ integers.
Answer:
positive
![]()
Question 5.
The integrating factor of the differential equation \(\frac{d y}{d x}\) – y = x is _________
Answer:
e-x
Question 6.
The differential equation by eliminating arbitrary constants from bx + ay = ab is _________
Answer:
\(\frac{d^{2} y}{d x^{2}}=0\)
(III) State whether each of the following is True or False:
Question 1.
The integrating factor of the differential equation \(\frac{d y}{d x}\) – y = x is e-x.
Answer:
True
Question 2.
The order and degree of a differential equation are always positive integers.
Answer:
True
Question 3.
The degree of a differential equation is the power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any.
Answer:
True
Question 4.
The order of highest derivative occurring in the differential equation is called the degree of the differential equation.
Answer:
False
![]()
Question 5.
The power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any is called the order of the differential equation.
Answer:
False
Question 6.
The degree of the differential equation \(e^{\frac{d y}{d x}}=\frac{d y}{d x}+c\) is not defined.
Answer:
True
(IV) Solve the following:
Question 1.
Find the order and degree of the following differential equations:
(i) \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3 / 2}=\frac{d^{2} y}{d x^{2}}\)
Solution:
The given differential equation is \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3 / 2}=\frac{d^{2} y}{d x^{2}}\)
∴ \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3}=\left(\frac{d^{2} y}{d x^{2}}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 3
∴ order = 3 and degree = 3
(ii) \(x+\frac{d y}{d x}=1+\left(\frac{d y}{d x}\right)^{2}\)
Solution:
The given differential equation is \(x+\frac{d y}{d x}=1+\left(\frac{d y}{d x}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d y}{d x}\) with power 2.
∴ order = 1, degree = 2.
Question 2.
Verify that y = log x + c is a solution of the differential equation \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\).
Solution:
y = log x + c
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{1}{x}+0=\frac{1}{x}\)
∴ x\(\frac{d y}{d x}\) = 1
Differentiating again w.r.t. x, we get
\(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \times 1=0\)
∴ \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)
This shows that y = log x + c is a solution of the D.E.
\(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)
![]()
Question 3.
Solve the following differential equations:
(i) \(\frac{d y}{d x}\) = 1 + x + y + xy
Solution:
\(\frac{d y}{d x}\) = 1 + x + y + xy
∴ \(\frac{d y}{d x}\) = (1 + x) + y(1 + x) = (1 + x)(1 + y)
∴ \(\frac{1}{1+y}\) dy = (1 + x) dx
Integrating, we get
∫\(\frac{1}{1+y}\) dy = ∫(1 + x) dx
∴ log|1 + y| = x + \(\frac{x^{2}}{2}\) + c
This is the general solution.
(ii) \(e^{d y / d x}=x\)
Solution:
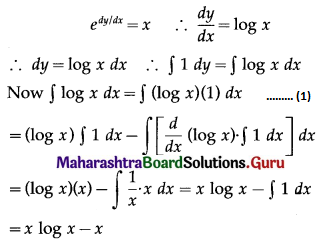
∴ from (1), the general solution is
y = x log x – x + c, i.e. y = x(log x – 1) + c.
(iii) dr = ar dθ – θ dr
Solution:
dr = ar dθ – θ dr
∴ dr + θ dr = ar dθ
∴ (1 + θ) dr = ar dθ
∴ \(\frac{d r}{r}=\frac{a d \theta}{1+\theta}\)
On integrating, we get
\(\int \frac{d r}{r}=a \int \frac{d \theta}{1+\theta}\)
∴ log |r| = a log |1 + θ| + c
This is the general solution.
(iv) Find the differential equation of the family of curves y = ex (ax + bx2), where a and b are arbitrary constants.
Solution:
y = ex (ax + bx2)
ax + bx2 = ye-x …….(1)
Differentiating (1) w.r.t. x twice and writing \(\frac{d y}{d x}\) as y1 and \(\frac{d^{2} y}{d x^{2}}\) as y2, we get


This is the required differential equation.
Question 4.
Solve \(\frac{d y}{d x}=\frac{x+y+1}{x+y-1}\) when x = \(\frac{2}{3}\) and y = \(\frac{1}{3}\).
Solution:


![]()
Question 5.
Solve y dx – x dy = -log x dx.
Solution:
y dx – x dy = -log x dx
∴ y dx – x dy + log x dx = 0
∴ x dy = (y + log x) dx
∴ \(\frac{d y}{d x}=\frac{y+\log x}{x}=\frac{y}{x}+\frac{\log x}{x}\)
∴ \(\frac{d y}{d x}-\frac{1}{x} \cdot y=\frac{\log x}{x}\) …….(1)
This is the linear differential equation of the form


This is the general solution.
Question 6.
Solve y log y \(\frac{d x}{d y}\) + x – log y = 0.
Solution:


Question 7.
Solve (x + y) dy = a2 dx
Solution:



Question 8.
Solve \(\frac{d y}{d x}+\frac{2}{x} y=x^{2}\)
Solution:
\(\frac{d y}{d x}+\frac{2}{x} y=x^{2}\) ……..(1)
This is a linear differential equation of the form

This is the general solution.
![]()
Question 9.
The rate of growth of the population is proportional to the number present. If the population doubled in the last 25 years and the present population is 1 lakh, when will the city have a population of 400000?
Solution:
Let P be the population at time t years.
Then the rate of growth of the population is \(\frac{d P}{d t}\) which is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant
∴ \(\frac{d P}{P}\)= k dt
On integrating, we get
\(\int \frac{d P}{P}=k \int d t\)
∴ log P = kt + c
The population doubled in 25 years and present population is 1,00,000.
∴ initial population was 50,000
i.e. when t = 0, P = 50000
∴ log 50000 = k × 0 + c
∴ c = log 50000
∴ log P = kt + log 50000
When t = 25, P = 100000
∴ log 100000 = k × 25 + log 50000
∴ 25k = log 100000 – log 50000 = log(\(\frac{100000}{50000}\))
∴ k = \(\frac{1}{25}\) log 2
∴ log P = \(\frac{t}{25}\) log 2 + log 50000
If P = 400000, then
log 400000 = \(\frac{t}{25}\) log 2 + log 50000
∴ log 400000 – log 50000 = \(\frac{t}{25}\) log 2
∴ log(\(\frac{400000}{50000}\)) = \(\log (2)^{t / 25}\)
∴ log 8 = \(\log (2)^{t / 25}\)
∴ 8 = \((2)^{t / 25}\)
∴ \((2)^{t / 25}\) = (2)3
∴ \(\frac{t}{25}\) = 3
∴ t = 75
∴ the population will be 400000 in (75 – 25) = 50 years.
Question 10.
The resale value of a machine decreases over a 10 years period at a rate that depends on the age of the machine. When the machine is x years old, the rate at which its value is changing is ₹ 2200(x – 10) per year. Express the value of the machine as a function of its age and initial value. If the machine was originally worth ₹ 1,20,000 how much will it be worth when it is 10 years old?
Solution:
Let V be the value of the machine after x years.
Then rate of change of the value is \(\frac{d V}{d x}\) which is 2200(x – 10)
∴ \(\frac{d V}{d x}\) = 2200(x – 10)
∴ dV = 2200(x – 10) dx
On integrating, we get
∫dV = 2200∫(x – 10) dx
∴ V = 2200[\(\frac{x^{2}}{2}\) – 10x] + c
Initially, i.e. at x = 0, V = 120000
∴ 120000 = 2200 × 0 + c = c
∴ c = 120000
∴ V = 2200[\(\frac{x^{2}}{2}\) – 10x] + 120000 …….(1)
This gives value of the machine in terms of initial value and age x.
We have to find V when x = 10.
When x = 10, from (1)
V = 2200[\(\frac{100}{2}\) – 100] + 120000
= 2200 [-50] + 120000
= -110000 + 120000
= 10000
Hence, the value of the machine after 10 years will be ₹ 10000.
![]()
Question 11.
Solve y2 dx + (xy + x2) dy = 0
Solution:
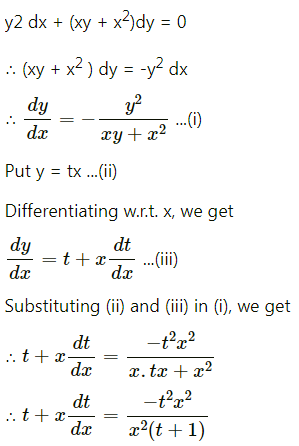
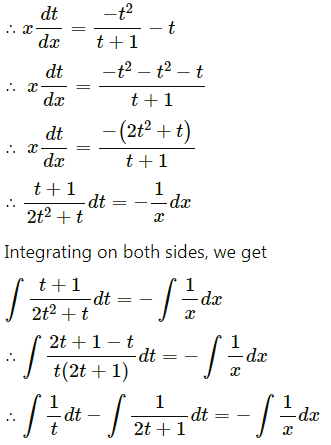
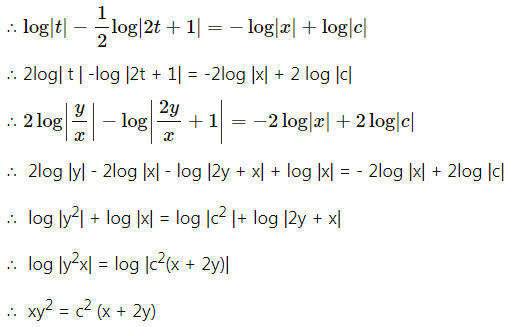
Question 12.
Solve x2y dx – (x3 + y3) dy = 0
Solution:
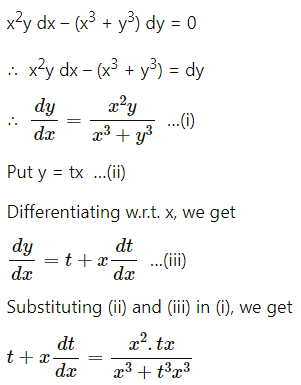

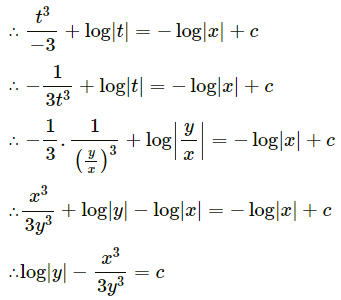
Question 13.
Solve yx \(\frac{d y}{d x}\) = x2 + 2y2
Solution:
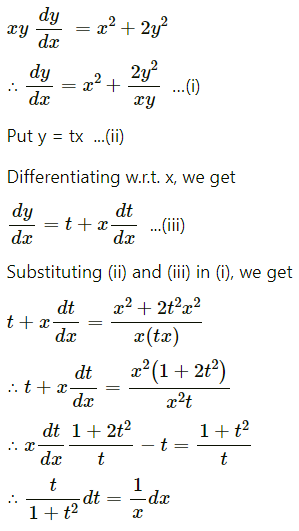
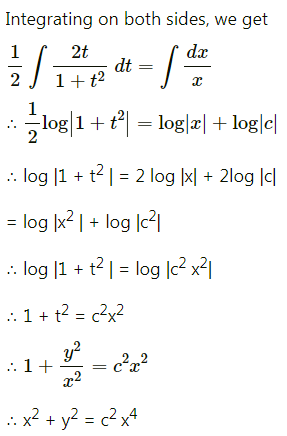
Question 14.
Solve (x + 2y3) \(\frac{d y}{d x}\) = y
Solution:
(x + 2y3) \(\frac{d y}{d x}\) = y
∴ x + 2y3 = y \(\frac{d x}{d y}\)

This is the general solution.
![]()
Question 15.
Solve y dx – x dy + log x dx = 0
Solution:
y dx – x dy + log x dx = 0
∴ (y + log x) dx = x dy


This is the general solution.
Question 16.
Solve \(\frac{d y}{d x}\) = log x dx
Solution:
\(\frac{d y}{d x}\) = log x dx
∴ dy = log x dx
On integrating, we get
∫dy = ∫log x . 1 dx
∴ y = (log x) ∫1 dx – \(\int\left[\left\{\frac{d}{d x}(\log x)\right\} \cdot \int 1 d x\right] d x\)
∴ y = (log x) . x – \(\int \frac{1}{x} \cdot x d x\)
∴ y = x log x – ∫1 dx
∴ y = x log x – x + c
This is the general solution.
Question 17.
y log y \(\frac{d x}{d y}\) = log y – x
Solution: