Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Differentiation Ex 1.1 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 1 Differentiation Ex 1.1
Question 1.
Differentiate the following w.r.t. x :
(i) (x3 – 2x – 1)5
Solution:
Method 1:
Let y = (x3 – 2x – 1)5
Put u = x3 – 2x – 1. Then y = u5
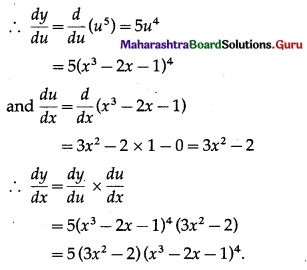
Method 2:
Let y = (x3 – 2x – 1)5
Differentiating w.r.t. x, we get
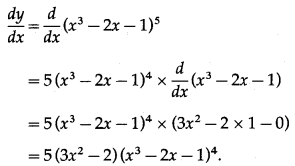
(ii) \(\left(2 x^{\frac{3}{2}}-3 x^{\frac{4}{3}}-5\right)^{\frac{5}{2}}\)
Solution:
Let y = \(\left(2 x^{\frac{3}{2}}-3 x^{\frac{4}{3}}-5\right)^{\frac{5}{2}}\)
Differentiating w.r.t. x, we get
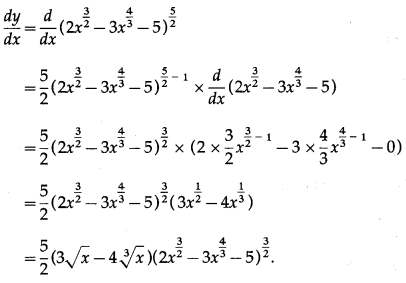
(iii) \(\sqrt{x^{2}+4 x-7}\)
Solution:
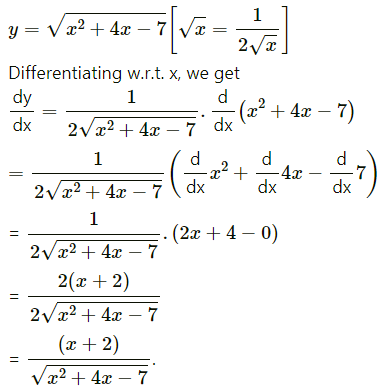
![]()
(iv) \(\sqrt{x^{2}+\sqrt{x^{2}+1}}\)
Solution:
Let y = \(\sqrt{x^{2}+\sqrt{x^{2}+1}}\)
Differentiating w.r.t. x, we get


(v) \(\frac{3}{5 \sqrt[3]{\left(2 x^{2}-7 x-5\right)^{5}}}\)
Solution:
Let y = \(\frac{3}{5 \sqrt[3]{\left(2 x^{2}-7 x-5\right)^{5}}}\)
Differentiating w.r.t. x, we get
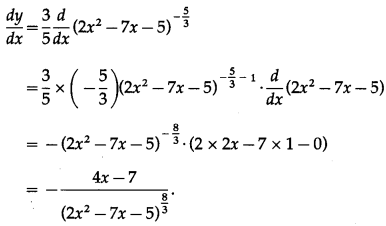
(vi) \(\left(\sqrt{3 x-5}-\frac{1}{\sqrt{3 x-5}}\right)^{5}\)
Solution:
Let y = \(\left(\sqrt{3 x-5}-\frac{1}{\sqrt{3 x-5}}\right)^{5}\)
Differentiating w.r.t. x, we get
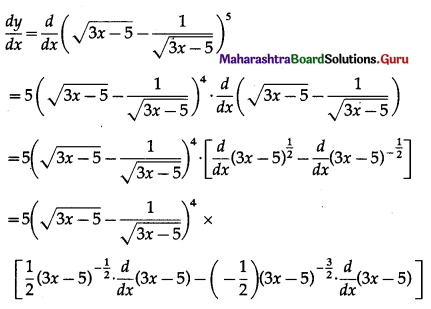
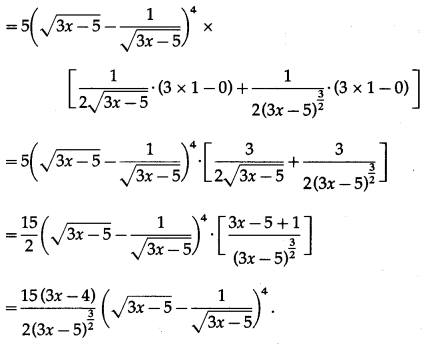
![]()
Question 2.
Diffrentiate the following w.r.t. x
(i) cos(x2 + a2)
Solution:
Let y = cos(x2 + a2)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)[cos(x2 + a2)]
= -sin(x2 + a2)∙\(\frac{d}{d x}\)x2 + a2)
= -sin(x2 + a2)∙(2x + 0)
= -2xsin(x2 + a2)
(ii) \(\sqrt{e^{(3 x+2)}+5}\)
Solution:
Let y = \(\sqrt{e^{(3 x+2)}+5}\)
Differentiating w.r.t. x, we get
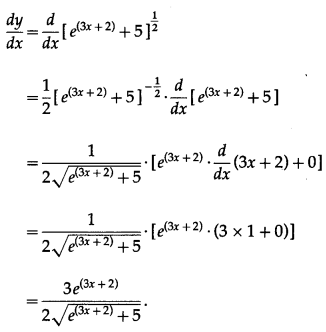
(iii) log[tan(\(\frac{x}{2}\))]
Solution:
Let y = log[tan(\(\frac{x}{2}\))]
Differentiating w.r.t. x, we get

![]()
(iv) \(\sqrt{\tan \sqrt{x}}\)
Solution:
Let y = \(\sqrt{\tan \sqrt{x}}\)
Differentiating w.r.t. x, we get
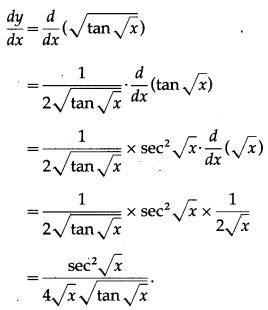
(v) cot3[log (x3)]
Solution:
Let y = cot3[log (x3)]
Differentiating w.r.t. x, we get
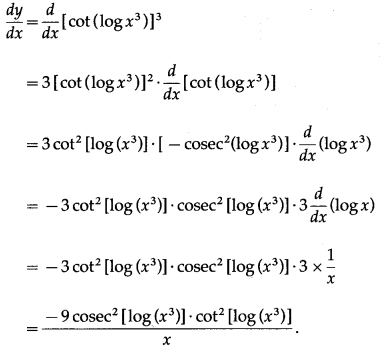
(vi) 5sin3x+ 3
Solution:
Let y = 5sin3x+ 3
Differentiating w.r.t. x, we get
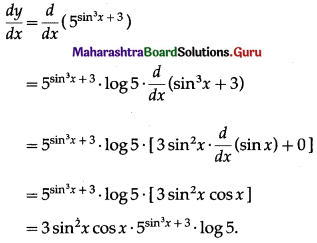
![]()
(vii) cosec (\(\sqrt{\cos X}\))
Solution:
Let y = cosec (\(\sqrt{\cos X}\))
Differentiating w.r.t. x, we get
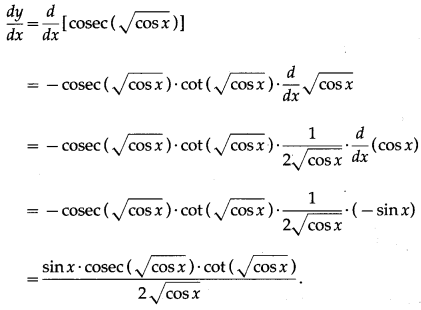
(viii) log[cos (x3 – 5)]
Solution:
Let y = log[cos (x3 – 5)]
Differentiating w.r.t. x, we get
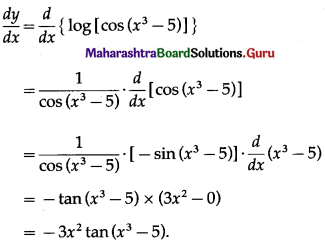
(ix) e3 sin2x – 2 cos2x
Solution:
Let y = e3 sin2x – 2 cos2x
Differentiating w.r.t. x, we get
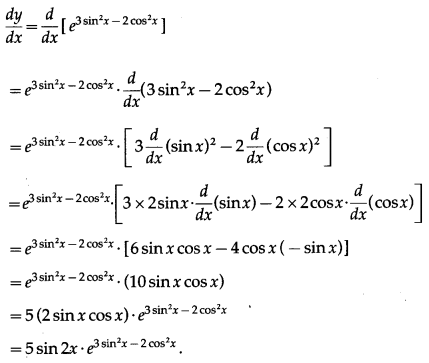
![]()
(x) cos2[log (x2+ 7)]
Solution:
Let y = cos2[log (x2+ 7)]
Differentiating w.r.t. x, we get
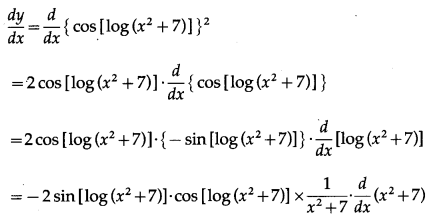
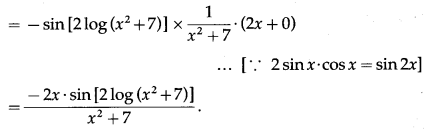
(xi) tan[cos (sinx)]
Solution:
Let y = tan[cos (sinx)]
Differentiating w.r.t. x, we get
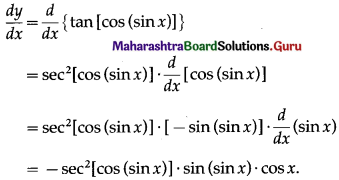
(xii) sec[tan (x4 + 4)]
Solution:
Let y = sec[tan (x4 + 4)]
Differentiating w.r.t. x, we get
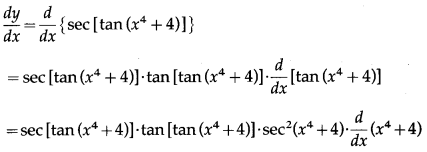
= sec[tan(x4 + 4)]∙tan[tan(x4 + 4)]∙sec2(x4 + 4)(4x3 + 0)
= 4x3sec2(x4 + 4)∙sec[tan(x4 + 4)]∙tan[tan(x4 + 4)].
(xiii) elog[(logx)2 – logx2]
Solution:
Let y = elog[(logx)2 – logx2]
= (log x)2 – log x2 …[∵ elog x = x]
Differentiating w.r.t. x, we get
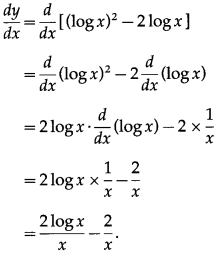
![]()
(xiv) sin\(\sqrt{\sin \sqrt{x}}\)
Solution:
Let y = sin\(\sqrt{\sin \sqrt{x}}\)
Differentiating w.r.t. x, we get

(xv) log[sec(ex2)]
Solution:
Let y = log[sec(ex2)]
Differentiating w.r.t. x, we get
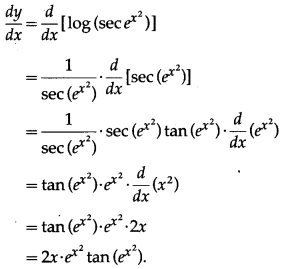
(xvi) loge2(logx)
Solution:
Let y = loge2(logx) = \(\frac{\log (\log x)}{\log e^{2}}\)
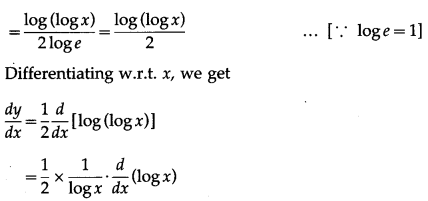
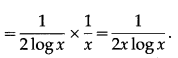
(xvii) [log{log(logx)}]2
Solution:
let y = [log{log(logx)}]2
Differentiating w.r.t. x, we get

![]()
(xviii) sin2x2 – cos2x2
Solution:
Let y = sin2x2 – cos2x2
Differentiating w.r.t. x, we get
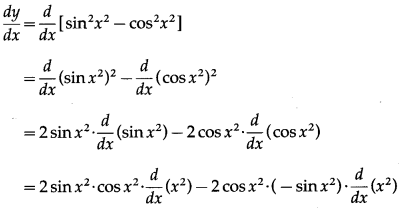
= 2sinx2∙cosx2 × 2x + 2sinx2∙cosx2 × 2x
= 4x(2sinx2∙cosx2)
= 4xsin(2x2).
Question 3.
Diffrentiate the following w.r.t. x
(i) (x2 + 4x + 1)3 + (x3 – 5x – 2)4
Solution:
Let y = (x2 + 4x + 1)3 + (x3 – 5x – 2)4
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)[(x2 + 4x + 1)3 + (x3 – 5x – 2)4]
= \(\frac{d}{d x}\) = (x2 + 4x + 1)3 + \(\frac{d}{d x}\)(x3 – 5x – 2)4
= 3(x2 + 4x + 1)2∙\(\frac{d}{d x}\)(x2 + 4x + 1) + 4(x3 – 5x – 2)4∙\(\frac{d}{d x}\)(x3 – 5x – 2)
= 3(x2 + 4x + 1)3∙(2x + 4 × 1 + 0) + 4(x3 – 5x – 2)3∙(3x2 – 5 × 1 – 0)
= 6 (x + 2)(x2 + 4x + 1)2 + 4 (3x2 – 5)(x3 – 5x – 2)3.
(ii) (1 + 4x)5(3 + x − x2)8
Solution:
Let y = (1 + 4x)5(3 + x − x2)8
Differentiating w.r.t. x, we get

= 8 (1 + 4x)5 (3 + x – x2)7∙(0 + 1 – 2x) + 5 (1 + 4x)4 (3 + x – x2)8∙(0 + 4 × 1)
= 8 (1 – 2x)(1 + 4x)5(3 + x – x2)7 + 20(1 + 4x)4(3 + x – x2)8.
(iii) \(\frac{x}{\sqrt{7-3 x}}\)
Solution:
Let y = \(\frac{x}{\sqrt{7-3 x}}\)
Differentiating w.r.t. x, we get
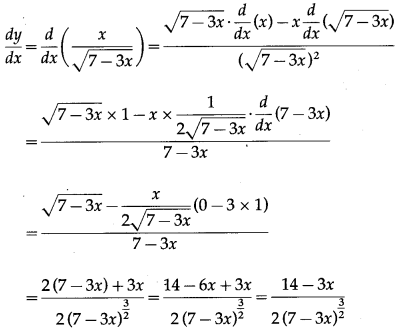
![]()
(iv) \(\frac{\left(x^{3}-5\right)^{5}}{\left(x^{3}+3\right)^{3}}\)
Solution:
Let y = \(\frac{\left(x^{3}-5\right)^{5}}{\left(x^{3}+3\right)^{3}}\)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\left[\frac{\left(x^{3}-5\right)^{5}}{\left(x^{3}+3\right)^{3}}\right]\)

(v) (1 + sin2x)2(1 + cos2x)3
Solution:
Let y = (1 + sin2x)2(1 + cos2x)3
Differentiating w.r.t. x, we get
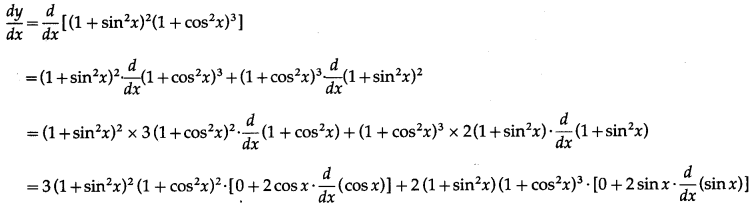
= 3(1 + sin2x)2 (1 + cos2x)2∙[2cosx(-sinx)] + 2 (1 + sin2x)(1 + cos2x)3∙[2sinx-cosx]
= 3 (1 + sin2x)2 (1 + cos2x)2 (-sin 2x) + 2(1 + sin2x)(1 + cos2x)3(sin 2x)
= sin2x (1 + sin2x) (1 + cos2x)2 [-3(1 + sin2x) + 2(1 + cos2x)]
= sin2x (1 + sin2x)(1 + cos2x)2(-3 – 3sin2x + 2 + 2cos2x)
= sin2x (1 + sin2x)(1 + cos2x)2 [-1 – 3 sin2x + 2 (1 – sin2x)]
= sin 2x(1 + sin2x)(1 + cos2x)2 (-1 – 3 sin2x + 2 – 2 sin2x)
= sin2x (1 + sin2x)(1 + cos2x)2(1 – 5 sin2x).
(vi) \(\sqrt{\cos x}+\sqrt{\cos \sqrt{x}}\)
Solution:
Let y = \(\sqrt{\cos x}+\sqrt{\cos \sqrt{x}}\)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}[\sqrt{\cos x}+\sqrt{\cos \sqrt{x}}]\)
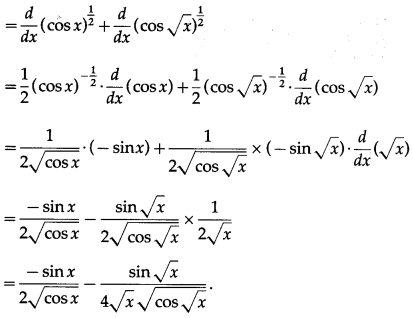
(vii) log(sec 3x+ tan 3x)
Solution:
Let y = log(sec 3x+ tan 3x)
Differentiating w.r.t. x, we get
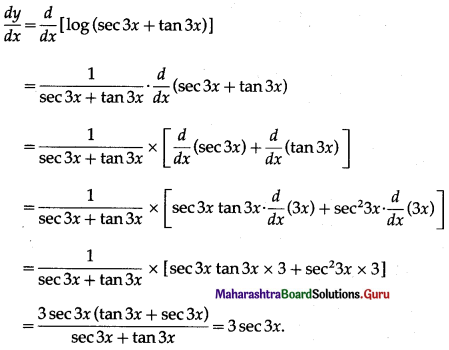
(viii) \(\frac{1+\sin x^{\circ}}{1-\sin x^{\circ}}\)
Solution:
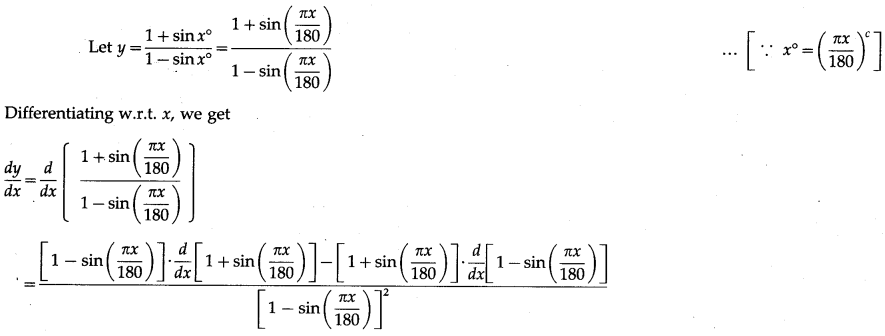

![]()
(ix) cot\(\left(\frac{\log x}{2}\right)\) – log\(\left(\frac{\cot x}{2}\right)\)
Solution:
Let y = cot\(\left(\frac{\log x}{2}\right)\) – log\(\left(\frac{\cot x}{2}\right)\)
Differentiating w.r.t. x, we get
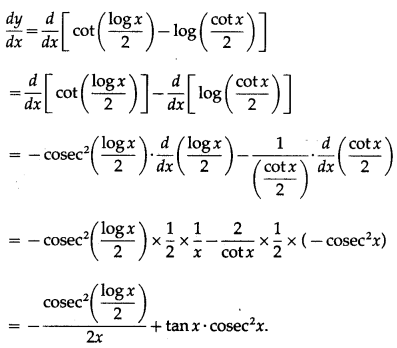
(x) \(\frac{e^{2 x}-e^{-2 x}}{e^{2 x}+e^{-2 x}}\)
Solution:


(xi) \(\frac{e^{\sqrt{x}}+1}{e^{\sqrt{x}}-1}\)
Solution:
let y = \(\frac{e^{\sqrt{x}}+1}{e^{\sqrt{x}}-1}\)
Differentiating w.r.t. x, we get
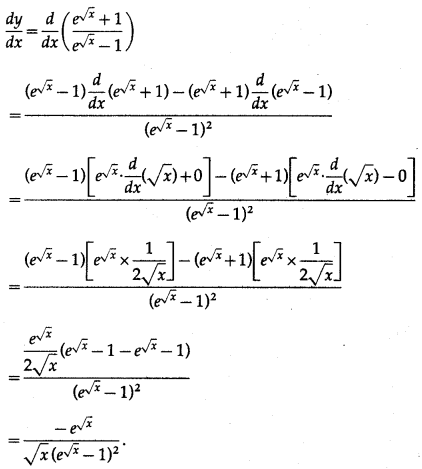
(xii) log[tan3x·sin4x·(x2 + 7)7]
Solution:
Let y = log [tan3x·sin4x·(x2 + 7)7]
= log tan3x + log sin4x + log (x2 + 7)7
= 3 log tan x + 4 log sin x + 7 log (x2 + 7)
Differentiating w.r.t. x, we get
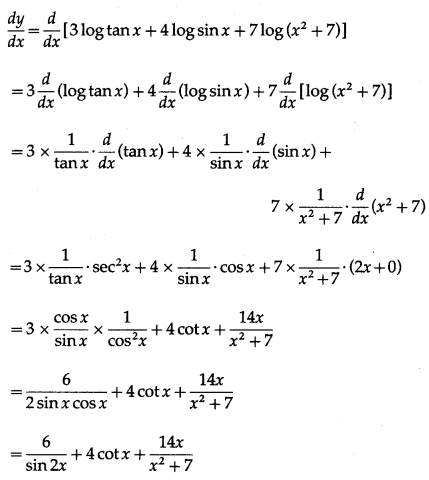
= 6cosec2x + 4 cotx + \(\frac{14 x}{x^{2}+7}\)
![]()
(xiii) log\(\left(\sqrt{\frac{1-\cos 3 x}{1+\cos 3 x}}\right)\)
Solution:

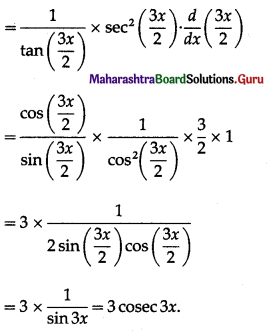
(xiv) log\(\left(\sqrt{\left.\frac{1+\cos \left(\frac{5 x}{2}\right)}{1-\cos \left(\frac{5 x}{2}\right)}\right)}\right.\)
Solution:
Using log\(\left(\frac{a}{b}\right)\) = log a – log b
log ab = b log a
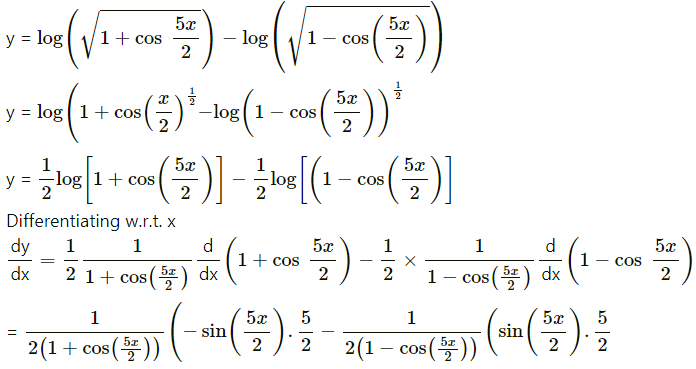
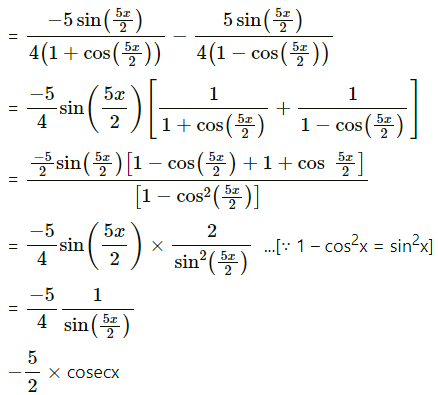
\(-\frac{5}{2}\)cosec\(\left(\frac{5 x}{2}\right)\)
(xv) log\(\left(\sqrt{\frac{1-\sin x}{1+\sin x}}\right)\)
Solution:

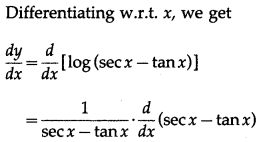
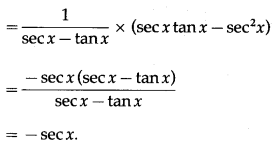
![]()
(xvi) log\(\left[4^{2 x}\left(\frac{x^{2}+5}{\sqrt{2 x^{3}-4}}\right)^{\frac{3}{2}}\right]\)
Solution:
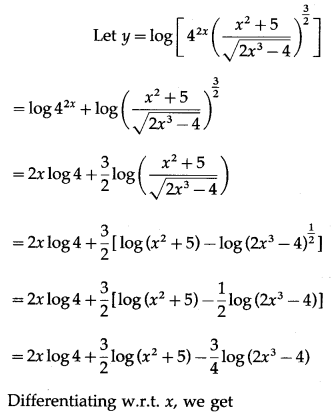
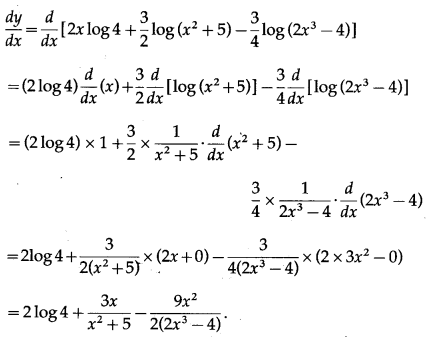
(xvii) log\(\left[\frac{e^{x^{2}}(5-4 x)^{\frac{3}{2}}}{\sqrt[3]{7-6 x}}\right]\)
Solution:
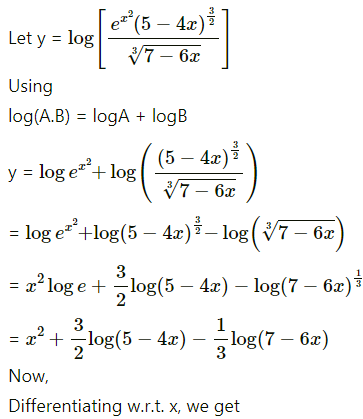
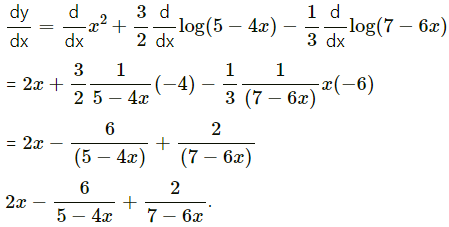
(xviii) log\(\left[\frac{a^{\cos x}}{\left(x^{2}-3\right)^{3} \log x}\right]\)
Solution:

(xix) y= (25)log5(secx) − (16)log4(tanx)
Solution:
y = (25)log5(secx) − (16)log4(tanx)
= 52log5(secx) – 42log4(tanx)
= 5log5(sec5x) – 4log4(tan2x)
= sec2x – tan2x … [∵ = x]
∴ y = 1
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(1) = 0
(xx) \(\frac{\left(x^{2}+2\right)^{4}}{\sqrt{x^{2}+5}}\)
Solution:
Let y = \(\frac{\left(x^{2}+2\right)^{4}}{\sqrt{x^{2}+5}}\)
Differentiating w.r.t. x, we get


![]()
Question 4.
A table of values of f, g, f ‘ and g’ is given
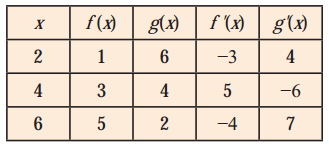
(i) If r(x) = f [g(x)] find r’ (2).
Solution:
r(x) = f[g(x)]
∴ r'(x) = \(\frac{d}{d x}\)f[g(x)]
= f'[g(x)]∙\(\frac{d}{d x}\)[g(x)]
= f'[g(x)∙[g'(x)]
∴ r'(2) = f'[g(2)]∙g'(2)
= f'(6)∙g'(2) … [∵ g(x) = 6, when x = 2]
= -4 × 4 … [From the table]
= -16.
(ii) If R(x) = g[3 + f(x)] find R’ (4).
Solution:
R(x) = g[3 + f(x)]
∴ R'(x) = \(\frac{d}{d x}\){g[3+f(x)]}
= g'[3 + f(x)]∙\(\frac{d}{d x}\)[3 + f(x)]
= g'[3 +f(x)]∙[0 + f'(x)]
= g'[3 + f(x)]∙f'(x)
∴ R'(4) = g'[3 + f(4)]∙f'(4)
= g'[3 + 3]∙f'(4) … [∵ f(x) = 3, when x = 4]
= g'(6)∙f'(4)
= 7 × 5 … [From the table]
= 35.
![]()
(iii) If s(x) = f[9− f(x)] find s’ (4).
Solution:
s(x) = f[9− f(x)]
∴ s'(x) = \(\frac{d}{d x}\){f[9 – f(x)]}
= f'[9 – f(x)]∙\(\frac{d}{d x}\)[0 – f(x)]
= f'[9 – f(x)]∙[0 – f'(x)]
= -f'[9 – f(x)] – f'(x)
∴ s'(4) = -f'[9 – f(4)] – f'(4)
= -f'[9 – 3] – f'(4) … [∵ f(x) = 3, when x = 4]
= -f'(6) – f'(4)
= -(-4)(5) … [From the table]
= 20.
(iv) If S(x) = g[g(x)] find S’ (6)
Solution:
S(x) = g[g(x)]
∴ S'(x) = \(\frac{d}{d x}\)g[g(x)]
= g'[g(x)]∙\(\frac{d}{d x}\)[g(x)]
= g'[g(x)]∙g'(x)
∴ S ‘(6) = g'[g'(6)]∙g'(6)
= g'(2)∙g'(6) … [∵ g (x) = 2, when x = 6]
= 4 × 7 … [From the table]
= 28.
![]()
Question 5.
Assume that f ‘(3) = -1, g'(2) = 5, g(2) = 3 and y = f[g(x)] then \(\left[\frac{d y}{d x}\right]_{x=2}\) = ?
Solution:
y = f[g(x)]
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\){[g(x)]}
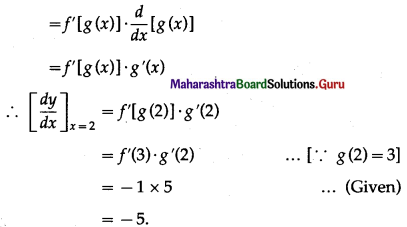
Question 6.
If h(x) = \(\sqrt{4 f(x)+3 g(x)}\), f(1) = 4, g(1) = 3, f ‘(1) = 3, g'(1) = 4 find h'(1).
Solution:
Given f(1) = 4, g(1) = 3, f ‘(1) = 3, g'(1) = 4 …..(1)
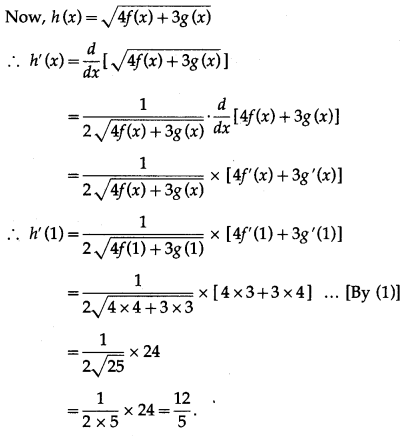
Question 7.
Find the x co-ordinates of all the points on the curve y = sin 2x – 2 sin x, 0 ≤ x < 2π where \(\frac{d y}{d x}\) = 0.
Solution:
y = sin 2x – 2 sin x, 0 ≤ x < 2π
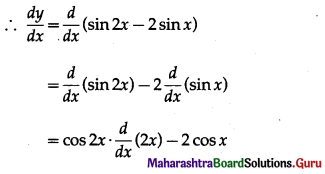
= cos2x × 2 – 2cosx
= 2 (2 cos2x – 1) – 2 cosx
= 4 cos2x – 2 – 2 cos x
= 4 cos2x – 2 cos x – 2
If \(\frac{d y}{d x}\) = 0, then 4 cos2x – 2 cos x – 2 = 0
∴ 4cos2x – 4cosx + 2cosx – 2 = 0
∴ 4 cosx (cosx – 1) + 2 (cosx – 1) = 0
∴ (cosx – 1)(4cosx + 2) = 0
∴ cosx – 1 = 0 or 4cosx + 2 = 0
∴ cos x = 1 or cos x = \(-\frac{1}{2}\)
∴ cos x = cos 0

![]()
Question 8.
Select the appropriate hint from the hint basket and fill up the blank spaces in the following paragraph. [Activity]
“Let f (x) = x2 + 5 and g(x) = ex + 3 then
f [g(x)] = _ _ _ _ _ _ _ _ and g [f(x)] =_ _ _ _ _ _ _ _.
Now f ‘(x) = _ _ _ _ _ _ _ _ and g'(x) = _ _ _ _ _ _ _ _.
The derivative off [g (x)] w. r. t. x in terms of f and g is _ _ _ _ _ _ _ _.
Therefore \(\frac{d}{d x}\)[f[g(x)]] = _ _ _ _ _ _ _ _ _ and [\(\frac{d}{d x}\)[f[g(x)]]]x = 0 = _ _ _ _ _ _ _ _ _ _ _.
The derivative of g[f(x)] w. r. t. x in terms of f and g is _ _ _ _ _ _ __ _ _ _ _.
Therefore \(\frac{d}{d x}\)[g[f(x)]] = _ _ _ _ _ _ _ _ _ and [\(\frac{d}{d x}\)[g[f(x)]]]x = 1 = _ _ _ _ _ _ _ _ _ _ _.”
Hint basket : { f ‘[g(x)]·g'(x), 2e2x + 6ex, 8, g'[f(x)]·f ‘(x), 2xex2 + 5, -2e6, e2x + 6ex + 14, ex2 + 5 + 3, 2x, ex}
Solution:
f[g(x)] = e2x + 6ex + 14
g[f(x)] = ex2 + 5 + 3
f'(x) = 2x, g’f(x) = ex
The derivative of f[g(x)] w.r.t. x in terms of and g is f'[g(x)]∙g'(x).
∴ \(\frac{d}{d x}\){f[g(x)]} = 2e2x + 6ex and \(\frac{d}{d x}\){f[g(x)]}x = 0 = 8
The derivative of g[f(x)] w.r.t. x in terms of f and g is g’f(x)]∙f'(x).
∴ \(\frac{d}{d x}\){g[(f(x)]} = 2xex2 + 5 and
\(\frac{d}{d x}\){g[(f(x)]}x = -1 = -2e6.