Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.3 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 3 Indefinite Integration Ex 3.3
I. Evaluate the following:
Question 1.
∫x2 log x dx
Solution:

Question 2.
∫x2 sin 3x dx
Solution:

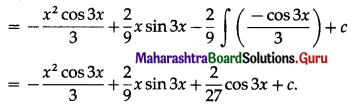
![]()
Question 3.
∫x tan-1 x dx
Solution:

Question 4.
∫x2 tan-1 x dx
Solution:

Question 5.
∫x3 tan-1 x dx
Solution:
Let I = ∫x3 tan-1 x dx
= ∫(tan-1 x) . x3 dx

Question 6.
∫(log x)2 dx
Solution:
Let I = ∫(log x)2 dx
Put log x = t

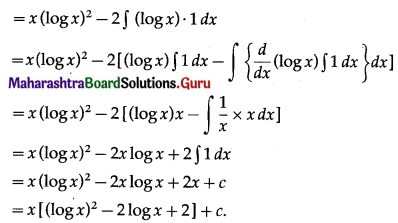
Question 7.
∫sec3 x dx
Solution:
Let I = ∫sec3 x dx
= ∫sec x sec2 x dx
= sec x ∫sec2 x dx – ∫[\(\frac{d}{d x}\)(sec x) ∫sec2 x dx] dx
= sec x tan x – ∫(sec x tan x)(tan x) dx
= sec x tan x – ∫sec x tan2 x dx
= sec x tan x – ∫sec x (sec2 x – 1) dx
= sec x tan x – ∫sec3 x dx + ∫sec x dx
∴ I = sec x tan x – I + log|sec x + tan x|
∴ 2I = sec x tan x + log|sec x + tan x|
∴ I = \(\frac{1}{2}\) [sec x tan x + log|sec x + tan x|] + c.
![]()
Question 8.
∫x . sin2 x dx
Solution:

Question 9.
∫x3 log x dx
Solution:
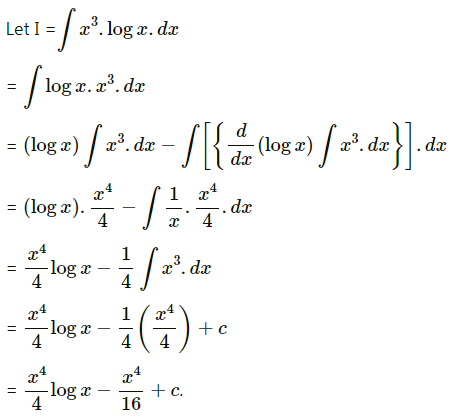
Question 10.
∫e2x cos 3x dx
Solution:

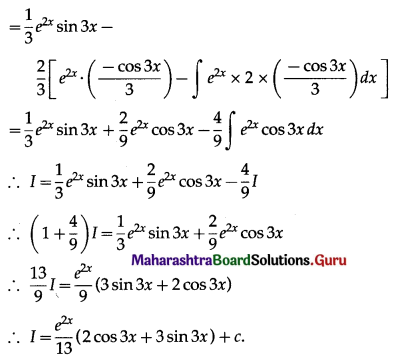
Question 11.
∫x sin-1 x dx
Solution:

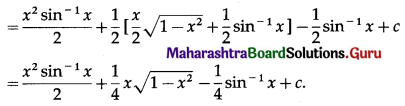
![]()
Question 12.
∫x2 cos-1 x dx
Solution:

Question 13.
\(\int \frac{\log (\log x)}{x} d x\)
Solution:

= t(log t – 1) + c
= (log x) . [log(log x) – 1] + c.
Question 14.
\(\int \frac{t \cdot \sin ^{-1} t}{\sqrt{1-t^{2}}} d t\)
Solution:

Question 15.
∫cos√x dx
Solution:
Let I = ∫cos√x dx
Put √x = t
∴ x = t2
∴ dx = 2t dt
∴ I = ∫(cos t) 2t dt
= ∫2t cos t dt
= 2t ∫cos t dt – ∫[\(\frac{d}{d t}\)(2t) ∫cos t dt]dt
= 2t sin t – ∫2 sin t dt
= 2t sin t + 2 cos t + c
= 2[√x sin√x + cos√x] + c.
![]()
Question 16.
∫sin θ . log(cos θ) dθ
Solution:
Let I = ∫sin θ . log (cos θ) dθ
= ∫log(cos θ) . sin θ dθ
Put cos θ = t
∴ -sin θ dθ = dt
∴ sin θ dθ = -dt
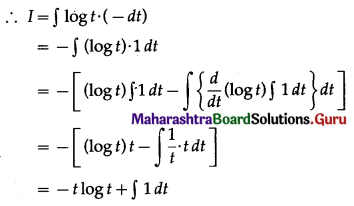
= -t log t + t + c
= -cos θ . log(cos θ) + cos θ + c
= -cos θ [log(cos θ) – 1] + c.
Question 17.
∫x cos3 x dx
Solution:
cos 3x = 4 cos3 x – 3 cos x
∴ cos3 x + 3 cos x = 4cos3x
∴ cos3 x = \(\frac{1}{4}\) cos 3x + \(\frac{3}{4}\) cos x

Question 18.
\(\int \frac{\sin (\log x)^{2}}{x} \cdot \log x d x\)
Solution:

![]()
Question 19.
\(\int \frac{\log x}{x} d x\)
Solution:
Let I = \(\int \frac{\log x}{x} d x\)
Put log x = t
\(\frac{1}{x}\) dx = dt
∴ I = ∫t dt
= \(\frac{1}{2}\) t2 + c
= \(\frac{1}{2}\) (log x)2 + c
Question 20.
∫x sin 2x cos 5x dx.
Solution:
Let I = ∫x sin 2x cos 5x dx
sin 2x cos 5x = \(\frac{1}{2}\)[2 sin 2x cos 5x]
= \(\frac{1}{2}\) [sin(2x + 5x) + sin(2x – 5x)]
= \(\frac{1}{2}\) [sin 7x – sin 3x]
∴ ∫sin 2x cos 5x dx = \(\frac{1}{2}\) [∫sin 7x dx – ∫sin 3x dx]

Question 21.
\(\int \cos (\sqrt[3]{x}) d x\)
Solution:
Let I = \(\int \cos (\sqrt[3]{x}) d x\)
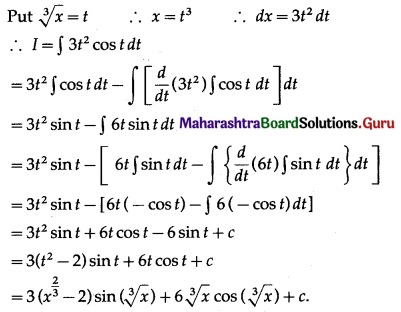
II. Integrate the following functions w.r.t. x:
Question 1.
e2x sin 3x
Solution:
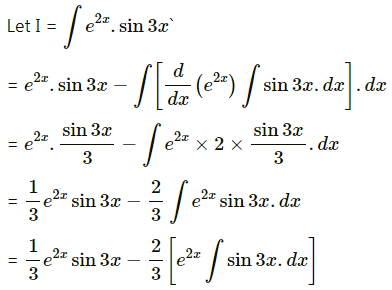
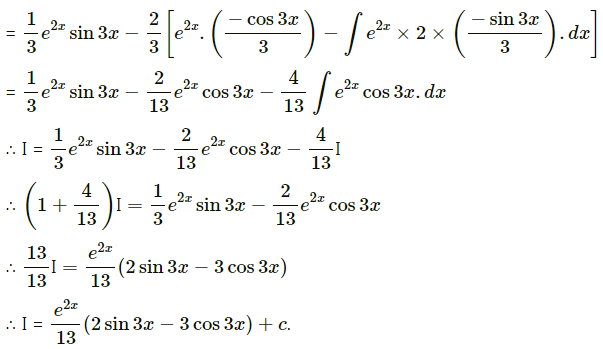
![]()
Question 2.
e-x cos 2x
Solution:
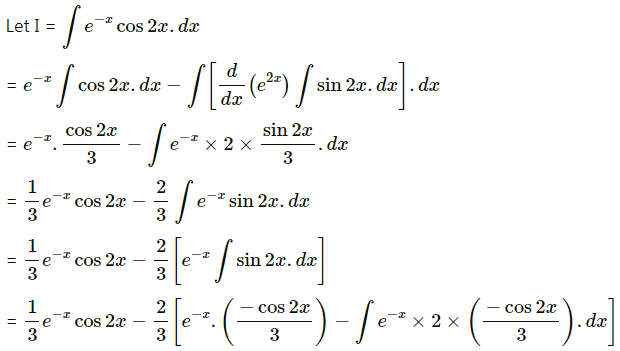
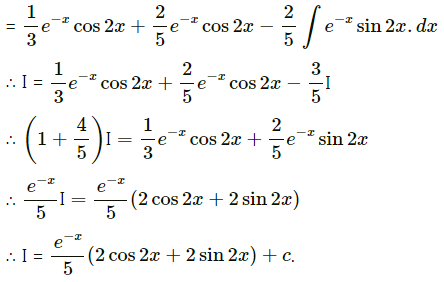
Question 3.
sin(log x)
Solution:

Question 4.
\(\sqrt{5 x^{2}+3}\)
Solution:
Let I = \(\sqrt{5 x^{2}+3}\) dx
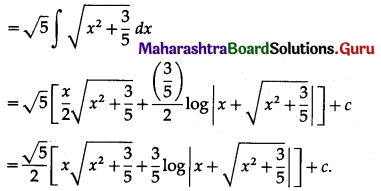
Question 5.
\(x^{2} \sqrt{a^{2}-x^{6}}\)
Solution:

Question 6.
\(\sqrt{(x-3)(7-x)}\)
Solution:
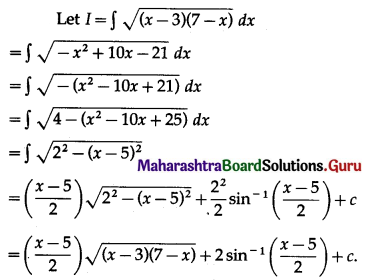
![]()
Question 7.
\(\sqrt{4^{x}\left(4^{x}+4\right)}\)
Solution:
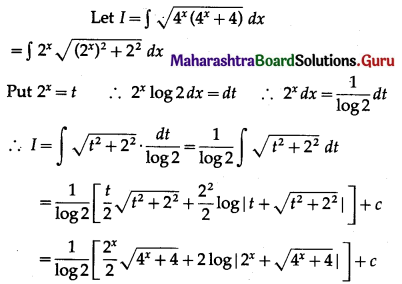
Question 8.
(x + 1) \(\sqrt{2 x^{2}+3}\)
Solution:
Let I = ∫(x + 1) \(\sqrt{2 x^{2}+3}\) dx
Let x + 1 = A[\(\frac{d}{d x}\)(2x2 + 3)] + B
= A(4x) + B
= 4Ax + B
Comparing the coefficients of x and constant term on both the sides, we get
4A = 1, B = 1
∴ A = \(\frac{1}{4}\), B = 1


Question 9.
\(x \sqrt{5-4 x-x^{2}}\)
Solution:
Let I = ∫\(x \sqrt{5-4 x-x^{2}}\) dx
Let x = A[\(\frac{d}{d x}\)(5 – 4x – x2)] + B
= A[-4 – 2x] + B
= -2Ax + (B – 4A)
Comparing the coefficients of x and the constant term on both sides, we get
-2A = 1, B – 4A = 0

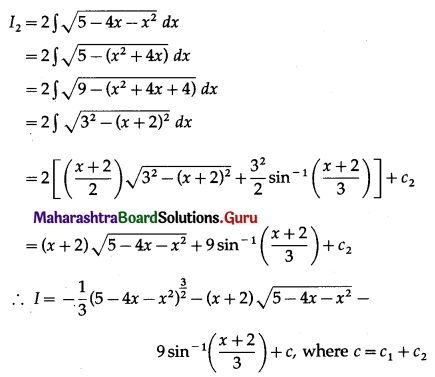
![]()
Question 10.
\(\sec ^{2} x \sqrt{\tan ^{2} x+\tan x-7}\)
Solution:

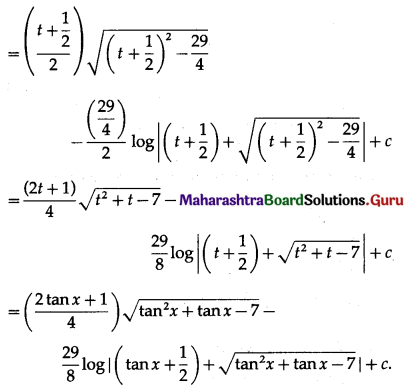
Question 11.
\(\sqrt{x^{2}+2 x+5}\)
Solution:

Question 12.
\(\sqrt{2 x^{2}+3 x+4}\)
Solution:


III. Integrate the following functions w.r.t. x:
Question 1.
[2 + cot x – cosec2 x] ex
Solution:
Let I = ∫ex [2 + cot x – cosec2 x] dx
Put f(x) = 2 + cot x
∴ f'(x) = \(\frac{d}{d x}\)(2 + cot x)
= \(\frac{d}{d x}\)(2) + \(\frac{d}{d x}\)(cot x)
= 0 – cosec2 x
= -cosec2 x
∴ I = ∫ex [f(x) + f'(x)] dx
= ex f(x) + c
= ex (2 + cot x) + c.
![]()
Question 2.
\(\left(\frac{1+\sin x}{1+\cos x}\right) e^{x}\)
Solution:

Question 3.
\(e^{x}\left(\frac{1}{x}-\frac{1}{x^{2}}\right)\)
Solution:
Let I = ∫\(e^{x}\left(\frac{1}{x}-\frac{1}{x^{2}}\right)\)
Let f(x) = \(\frac{1}{x}\), f'(x) = \(-\frac{1}{x^{2}}\)
∴ I = ∫ex [f(x) + f'(x)] dx
= ex f(x) + c
= ex . \(\frac{1}{x}\) + c
Question 4.
\(\left[\frac{x}{(x+1)^{2}}\right] e^{x}\)
Solution:

Question 5.
\(\frac{e^{x}}{x}\) . [x(log x)2 + 2 log x]
Solution:
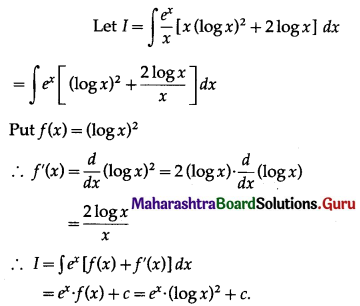
![]()
Question 6.
\(e^{5 x}\left[\frac{5 x \log x+1}{x}\right]\)
Solution:
Let I = ∫\(e^{5 x}\left[\frac{5 x \log x+1}{x}\right]\)

Question 7.
\(e^{\sin ^{-1} x}\left[\frac{x+\sqrt{1-x^{2}}}{\sqrt{1-x^{2}}}\right]\)
Solution:

Question 8.
log(1 + x)(1+x)
Solution :
Let I = ∫log(1 + x)(1+x) dx
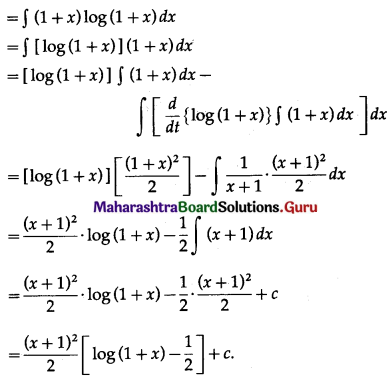
![]()
Question 9.
cosec (log x)[1 – cot(log x)]
Solution:
Let I = ∫cosec (log x)[1 – cot(log x)] dx
Put log x = t
x = et
dx = et dt
I = ∫cosec t (1 – cot t). et dt
= ∫et [cosec t – cosec t cot t] dt
= ∫et [cosec t + \(\frac{d}{d t}\) (cosec t)] dt
= et cosec t + c ….. [∵ et [f(t) +f'(t) ] dt = et f(t) + c ]
= x . cosec(log x) + c.