Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Miscellaneous Exercise 3 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 3 Indefinite Integration Miscellaneous Exercise 3
I. Choose the correct options from the given alternatives:
Question 1.
\(\int \frac{1+x+\sqrt{x+x^{2}}}{\sqrt{x}+\sqrt{1+x}} \cdot d x=\)
(a) \(\frac{1}{2} \sqrt{x+1}+c\)
(b) \(\frac{2}{3}(x+1)^{\frac{3}{2}}+c\)
(c) \(\sqrt{x+1}+c\)
(d) \(2(x+1)^{\frac{3}{2}}+c\)
Answer:
(b) \(\frac{2}{3}(x+1)^{\frac{3}{2}}+c\)
![]()
Question 2.
\(\int \frac{1}{x+x^{5}} \cdot d x\) = f(x) + c, then \(\int \frac{x^{4}}{x+x^{5}} \cdot d x=\)
(a) log x – f(x) + c
(b) f(x) + log x + c
(c) f(x) – log x + c
(d) \(\frac{1}{5}\) x5 f(x) + c
Answer:
(a) log x – f(x) + c
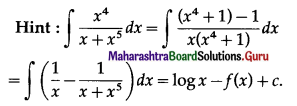
Question 3.
\(\int \frac{\log (3 x)}{x \log (9 x)} \cdot d x=\)
(a) log(3x) – log(9x) + c
(b) log(x) – (log 3) . log(log 9x) + c
(c) log 9 – (log x) . log(log 3x) + c
(d) log(x) + log(3) . log(log 9x) + c
Answer:
(b) log(x) – (log 3) . log(log 9x) + c

Question 4.
\(\int \frac{\sin ^{m} X}{\cos ^{m+2} X} \cdot d x=\)
(a) \(\frac{\tan ^{m+1} \boldsymbol{X}}{m+1}+c\)
(b) (m + 2) tanm+1 x + c
(c) \(\frac{\tan ^{m} \boldsymbol{X}}{m}+c\)
(d) (m + 1) tanm+1 x + c
Answer:
(a) \(\frac{\tan ^{m+1} \boldsymbol{X}}{m+1}+c\)
Question 5.
∫tan(sin-1 x) . dx =
(a) \(\left(1-x^{2}\right)^{-\frac{1}{2}}+c\)
(b) \(\left(1-x^{2}\right)^{\frac{1}{2}}+c\)
(c) \(\frac{\tan ^{m} \boldsymbol{X}}{\sqrt{1-x^{2}}}+c\)
(d) \(-\sqrt{1-x^{2}}+c\)
Answer:
(d) \(-\sqrt{1-x^{2}}+c\)
Hint: sin-1 x = \(\tan ^{-1}\left(\frac{x}{\sqrt{1-x^{2}}}\right)\)
![]()
Question 6.
\(\int \frac{x-\sin x}{1-\cos x} \cdot d x=\)
(a) x cot(\(\frac{x}{2}\)) + c
(b) -x cot(\(\frac{x}{2}\)) + c
(c) cot(\(\frac{x}{2}\)) + c
(d) x tan(\(\frac{x}{2}\)) + c
Answer:
(b) -x cot(\(\frac{x}{2}\)) + c

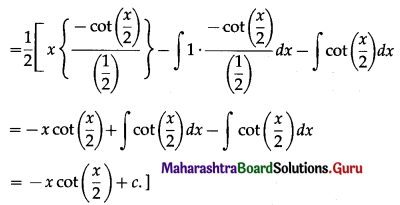
Question 7.
If f(x) = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\), g(x) = \(e^{\sin ^{-1} x}\), then ∫f(x) . g(x) . dx =
(a) \(e^{\sin ^{-1} x} \cdot\left(\sin ^{-1} x-1\right)+c\)
(b) \(e^{\sin ^{-1} x} \cdot\left(1-\sin ^{-1} x\right)+c\)
(c) \(e^{\sin ^{-1} x} \cdot\left(\sin ^{-1} x+1\right)+c\)
(d) \(e^{\sin ^{-1} x} \cdot\left(\sin ^{-1} X-1\right)+c\)
Answer:
(a) \(e^{\sin ^{-1} x} \cdot\left(\sin ^{-1} x-1\right)+c\)
Question 8.
If ∫tan3 x . sec3 x . dx = (\(\frac{1}{m}\)) secm x – (\(\frac{1}{n}\)) secn x + c, then (m, n) =
(a) (5, 3)
(b) (3, 5)
(c) \(\left(\frac{1}{5}, \frac{1}{3}\right)\)
(d) (4, 4)
Answer:
(a) (5, 3)
Hint: ∫tan3 x . sec3 x dx
= ∫sec2 x . tan2 x . sec x tan x dx
= ∫sec2 x (sec2 x – 1) sec x tan x dx
Put sec x = t.
Question 9.
\(\int \frac{1}{\cos x-\cos ^{2} x} \cdot d x=\)
(a) log(cosec x – cot x) + tan(\(\frac{x}{2}\)) + c
(b) sin 2x – cos x + c
(c) log(sec x + tan x) – cot(\(\frac{x}{2}\)) + c
(d) cos 2x – sin x + c
Answer:
(c) log(sec x + tan x) – cot(\(\frac{x}{2}\)) + c

Question 10.
\(\int \frac{\sqrt{\cot x}}{\sin x \cdot \cos x} \cdot d x=\)
(a) \(2 \sqrt{\cot x}+c\)
(b) \(-2 \sqrt{\cot x}+c\)
(c) \(\frac{1}{2} \sqrt{\cot x}+c\)
(d) \(\sqrt{\cot X}+c\)
Answer:
(b) \(-2 \sqrt{\cot x}+c\)
![]()
Question 11.
\(\int \frac{e^{x}(x-1)}{x^{2}} \cdot d x=\)
(a) \(\frac{e^{x}}{x}+c\)
(b) \(\frac{e^{x}}{x^{2}}+c\)
(c) \(\left(x-\frac{1}{x}\right) e^{x}+c\)
(d) x e-x + c
Answer:
(a) \(\frac{e^{x}}{x}+c\)
Question 12.
∫sin(log x) . dx =
(a) \(\frac{x}{2}\) [sin(log x) – cos(log x)] + c
(b) \(\frac{x}{2}\) [sin(log x) + cos(log x)] + c
(c) \(\frac{x}{2}\) [cos(log x) – sin(log x)] + c
(d) \(\frac{x}{4}\) [cos(log x) – sin(log x)] + c
Answer:
(a) \(\frac{x}{2}\) [sin(log x) – cos(log x)] + c
Question 13.
∫xx (1 + log x) . dx =
(a) \(\frac{1}{2}\) (1 + log x)2 + c
(b) x2x + c
(c) xx log x + c
(d) xx + c
Answer:
(d) xx + c
Hint: \(\frac{d}{d x}\)(xx) = xx (1 + log x)
Question 14.
\(\int \cos ^{-\frac{3}{7}} x \cdot \sin ^{-\frac{11}{7}} x \cdot d x=\)
(a) \(\log \left(\sin ^{-\frac{4}{7}} x\right)+c\)
(b) \(\frac{4}{7} \tan ^{\frac{4}{7}} x+c\)
(c) \(-\frac{7}{4} \tan ^{-\frac{4}{7}} x+c\)
(d) \(\log \left(\cos ^{\frac{3}{7}} x\right)+c\)
Answer:
(c) \(-\frac{7}{4} \tan ^{-\frac{4}{7}} x+c\)
Hint: \(\int \cos ^{-\frac{3}{7}} x \sin ^{-\frac{11}{7}} x d x\)
= \(\int \frac{\sin ^{-\frac{11}{7}} x}{\cos ^{-\frac{11}{7}} x \cdot \cos ^{2} x} d x\)
= \(\int \tan ^{-\frac{11}{7}} x \sec ^{2} x d x\)
Put tan x = t.
Question 15.
\(2 \int \frac{\cos ^{2} x-\sin ^{2} x}{\cos ^{2} x+\sin ^{2} x} \cdot d x=\)
(a) sin 2x + c
(b) cos 2x + c
(c) tan 2x + c
(d) 2 sin 2x + c
Answer:
(a) sin 2x + c
![]()
Question 16.
\(\int \frac{d x}{\cos x \sqrt{\sin ^{2} x-\cos ^{2} x}} \cdot d x=\)
(a) log(tan x – \(\sqrt{\tan ^{2} x-1}\)) + c
(b) sin-1 (tan x) + c
(c) 1 + sin-1 (cot x) + c
(d) log(tan x + \(\sqrt{\tan ^{2} x-1}\)) + c
Answer:
(d) log(tan x + \(\sqrt{\tan ^{2} x-1}\)) + c
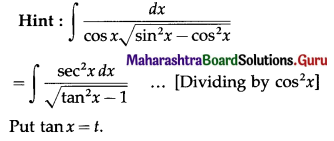
Question 17.
\(\int \frac{\log x}{(\log e x)^{2}} \cdot d x=\)
(a) \(\frac{x}{1+\log x}+c\)
(b) x(1 + log x) + c
(c) \(\frac{1}{1+\log x}+c\)
(d) \(\frac{1}{1-\log x}+c\)
Answer:
(a) \(\frac{x}{1+\log x}+c\)
Question 18.
∫[sin(log x) + cos(log x)] . dx =
(a) x cos(log x) + c
(b) sin(log x) + c
(c) cos(log x) + c
(d) x sin(log x) + c
Answer:
(d) x sin(log x) + c
Question 19.
\(\int \frac{\cos 2 x-1}{\cos 2 x+1} \cdot d x=\)
(a) tan x – x + c
(b) x + tan x + c
(c) x – tan x + c
(d) -x – cot x + c
Answer:
(c) x – tan x + c

Question 20.
\(\int \frac{e^{2 x}+e^{-2 x}}{e^{x}} \cdot d x=\)
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)
(b) \(e^{x}+\frac{1}{3 e^{3 x}}+c\)
(c) \(e^{-x}+\frac{1}{3 e^{3 x}}+c\)
(d) \(e^{-x}-\frac{1}{3 e^{3 x}}+c\)
Answer:
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)

II. Integrate the following with respect to the respective variable:
Question 1.
(x – 2)2 √x
Solution:

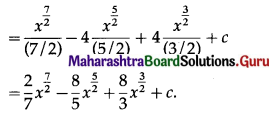
Question 2.
\(\frac{x^{7}}{x+1}\)
Solution:

![]()
Question 3.
\((6 x+5)^{\frac{3}{2}}\)
Solution:
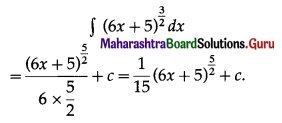
Question 4.
\(\frac{t^{3}}{(t+1)^{2}}\)
Solution:

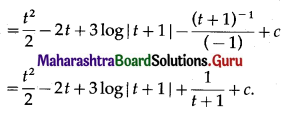
Question 5.
\(\frac{3-2 \sin x}{\cos ^{2} x}\)
Solution:

Question 6.
\(\frac{\sin ^{6} \theta+\cos ^{6} \theta}{\sin ^{2} \theta \cdot \cos ^{2} \theta}\)
Solution:

![]()
Question 7.
cos 3x cos 2x cos x
Solution:


Question 8.
\(\frac{\cos 7 x-\cos 8 x}{1+2 \cos 5 x}\)
Solution:


Question 9.
\(\cot ^{-1}\left(\frac{1+\sin x}{\cos x}\right)\)
Solution:
Let I = \(\int \cot ^{-1}\left(\frac{1+\sin x}{\cos x}\right) d x\)

III. Integrate the following w.r.t. x:
Question 1.
\(\frac{(1+\log x)^{3}}{x}\)
Solution:

![]()
Question 2.
cot-1 (1 – x + x2)
Solution:





Question 3.
\(\frac{1}{x \sin ^{2}(\log x)}\)
Solution:
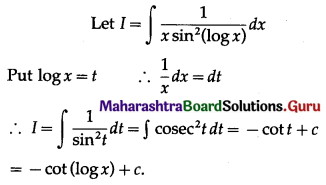
Question 4.
\(\sqrt{x} \sec \left(x^{\frac{3}{2}}\right) \tan \left(x^{\frac{3}{2}}\right)\)
Solution:

Question 5.
log(1 + cos x) – x tan(\(\frac{x}{2}\))
Solution:

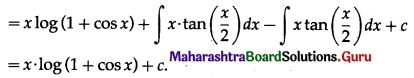
Question 6.
\(\frac{x^{2}}{\sqrt{1-x^{6}}}\)
Solution:

![]()
Question 7.
\(\frac{1}{(1-\cos 4 x)(3-\cot 2 x)}\)
Solution:
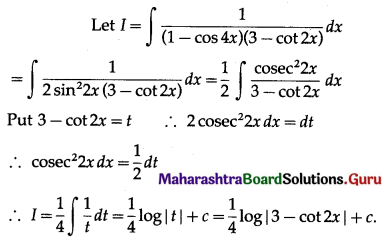
Question 8.
log(log x) + (log x)-2
Solution:


Question 9.
\(\frac{1}{2 \cos x+3 \sin x}\)
Solution:




Question 10.
\(\frac{1}{x^{3} \sqrt{x^{2}-1}}\)
Solution:


![]()
Question 11.
\(\frac{3 x+1}{\sqrt{-2 x^{2}+x+3}}\)
Solution:

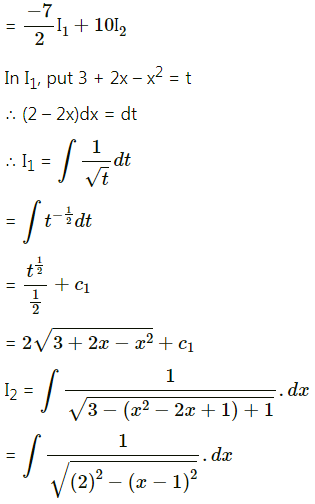
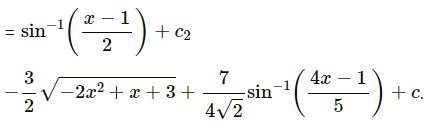
Question 12.
log(x2 + 1)
Solution:

Question 13.
e2x sin x cos x
Solution:
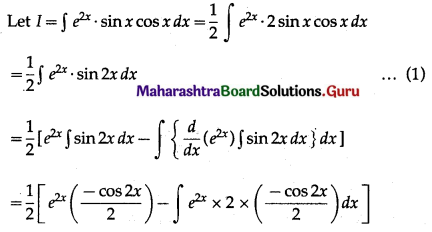

Question 14.
\(\frac{x^{2}}{(x-1)(3 x-1)(3 x-2)}\)
Solution:
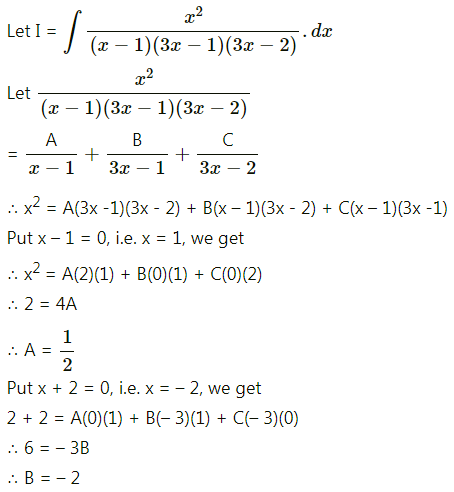
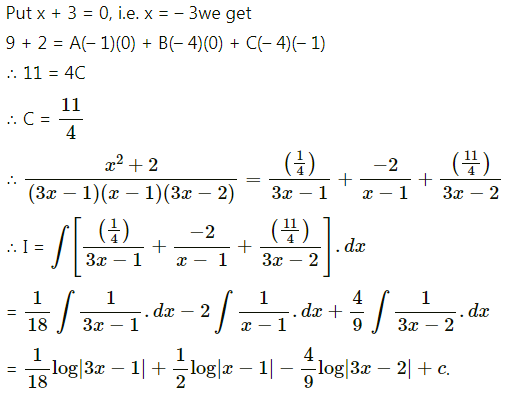
Question 15.
\(\frac{1}{\sin x+\sin 2 x}\)
Solution:
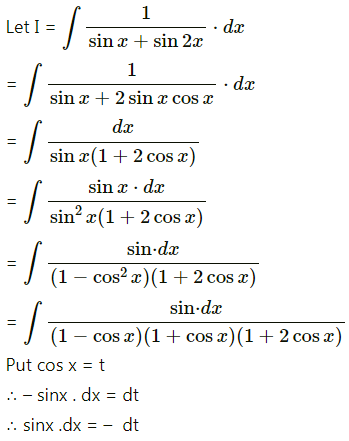
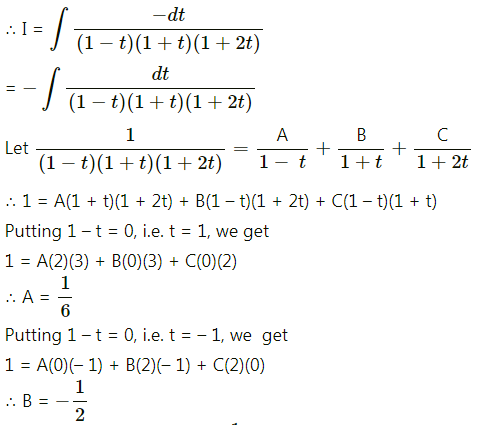
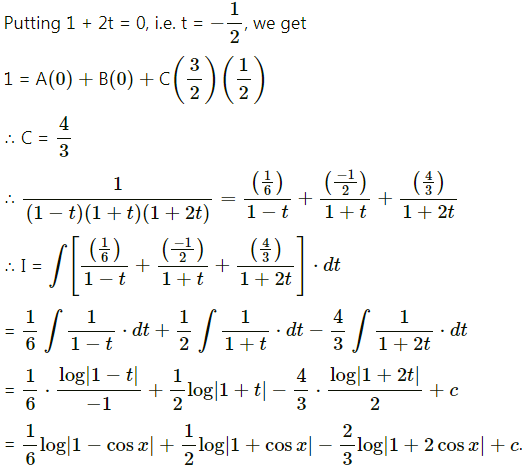
![]()
Question 16.
\(\sec ^{2} x \sqrt{7+2 \tan x-\tan ^{2} x}\)
Solution:
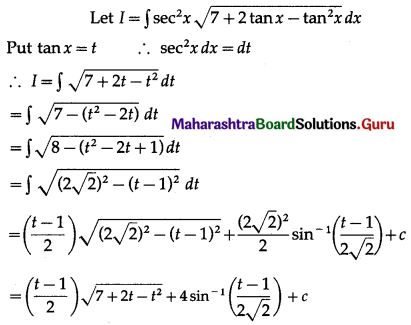
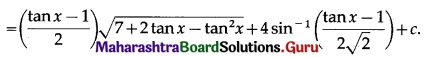
Question 17.
\(\frac{x+5}{x^{3}+3 x^{2}-x-3}\)
Solution:
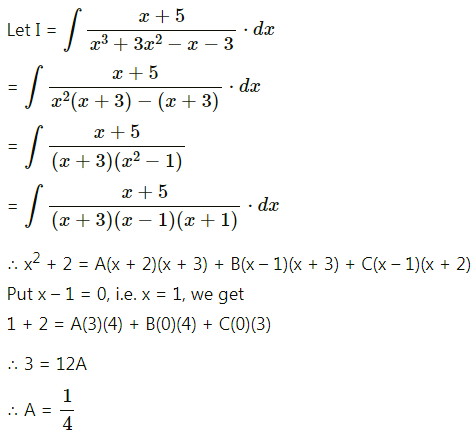
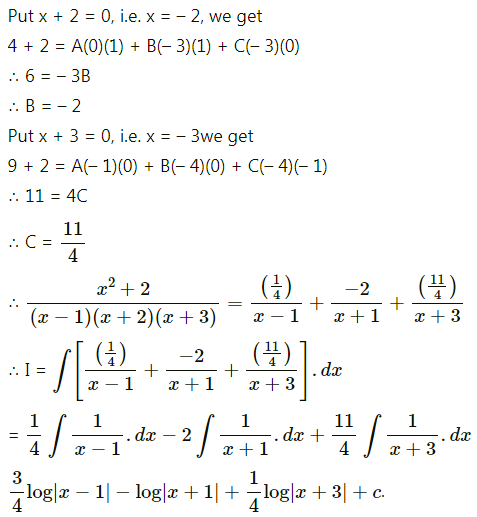
Question 18.
\(\frac{1}{x\left(x^{5}+1\right)}\)
Solution:
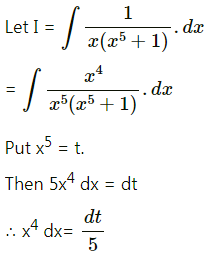
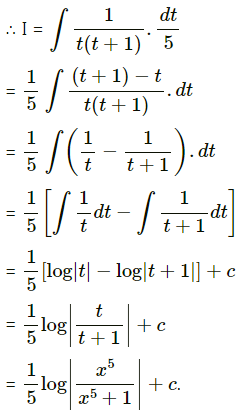
Question 19.
\(\frac{\sqrt{\tan x}}{\sin x \cdot \cos x}\)
Solution:

![]()
Question 20.
sec4 x cosec2 x
Solution:
