Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Definite Integration Ex 4.1 Questions and Answers.
12th Maths Part 2 Definite Integration Exercise 4.1 Questions And Answers Maharashtra Board
I. Evaluate the following integrals as a limit of a sum.
Question 1.
\(\int_{1}^{3}(3 x-4) \cdot d x\)
Solution:
Let f(x) = 3x – 4, for 1 ≤ x ≤ 3
Divide the closed interval [1, 3] into n subintervals each of length h at the points
1, 1 + h, 1 + 2h, 1 + rh, ….., 1 + nh = 3
∴ nh = 2
∴ h = \(\frac{2}{n}\) and as n → ∞, h → 0
Here, a = 1
∴ f(a + rh) = f(1 + rh)
= 3(1 + rh) – 4
= 3rh – 1
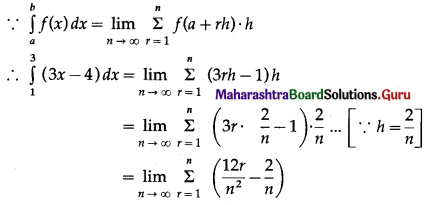

![]()
Question 2.
\(\int_{0}^{4} x^{2} d x\)
Solution:
Let f(x) = x2, for 0 ≤ x ≤ 4
Divide the closed interval [0, 4] into n subintervals each of length h at the points
0, 0 + h, 0 + 2h, ….., 0 + rh, ….., 0 + nh = 4
i.e. 0, h, 2h, ….., rh, ….., nh = 4
∴ h = \(\frac{4}{n}\) as n → ∞, h → 0
Here, a = 0

Question 3.
\(\int_{0}^{2} e^{x} d x\)
Solution:
Let f(x) = ex, for 0 ≤ x ≤ 2
Divide the closed interval [0, 2] into n equal subntervals each of length h at the points
0, 0 + h, 0 + 2h, ….., 0 + rh, ….., 0 + nh = 2
i.e. 0, h, 2h, ….., rh, ….., nh = 2
∴ h = \(\frac{2}{n}\) and as n → ∞, h → 0
Here, a = 0


![]()
Question 4.
\(\int_{0}^{2}\left(3 x^{2}-1\right) d x\)
Solution:
Let f(x) = 3x2 – 1, for 0 ≤ x ≤ 2
Divide the closed interval [0, 2] into n subintervals each of length h at the points.
0, 0 + h, 0 + 2h, ….., 0 + rh, ……, 0 + nh = 2
i.e. 0, h, 2h, ….., rh, ….., nh = 2
∴ h = \(\frac{2}{n}\) and as n → ∞, h → 0
Here, a = 0
∴ f(a + rh) = f(0 + rh)
= f(rh)
= 3(rh)2 – 1
= 3r2h2 – 1

![]()
Question 5.
\(\int_{1}^{3} x^{3} d x\)
Solution:
Let f(x) = x3, for 1 ≤ x ≤ 3.
Divide the closed interval [1, 3] into n equal su bintervals each of length h at the points
1, 1 + h, 1 + 2h, ……, 1 + rh, ……, 1 + nh = 3
∴ nh = 2
∴ h = \(\frac{2}{n}\) and as n → ∞, h → 0
Here a = 1


12th Maharashtra State Board Maths Solutions Pdf Part 2
- Definite Integration Ex 4.1 Class 12 Maths Solutions
- Definite Integration Ex 4.2 Class 12 Maths Solutions
- Definite Integration Miscellaneous Exercise 4 Class 12 Maths Solutions
- Application of Definite Integration Ex 5.1 Class 12 Maths Solutions
- Application of Definite Integration Miscellaneous Exercise 5 Class 12 Maths Solutions