Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Application of Definite Integration Ex 5.1 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 5 Application of Definite Integration Ex 5.1
1. Find the area of the region bounded by the following curves, X-axis, and the given lines:
(i) y = 2x, x = 0, x = 5.
Solution:
Required area = \(\int_{0}^{5} y d x\), where y = 2x
= \(\int_{0}^{5} 2x d x\)
= \(\left[\frac{2 x^{2}}{2}\right]_{0}^{5}\)
= 25 – 0
= 25 sq units.
(ii) x = 2y, y = 0, y = 4.
Solution:
Required area = \(\int_{0}^{4} x d y\), where x = 2y
= \(\int_{0}^{4} 2 y d y\)
= \(\left[\frac{2 y^{2}}{2}\right]_{0}^{4}\)
= 16 – 0
= 16 sq units.
![]()
(iii) x = 0, x = 5, y = 0, y = 4.
Solution:
Required area = \(\int_{0}^{5} y d x\), where y = 4
= \(\int_{0}^{5} 4 d x\)
= \([4 x]_{0}^{5}\)
= 20 – 0
= 20 sq units.
(iv) y = sin x, x = 0, x = \(\frac{\pi}{2}\)
Solution:
Required area = \(\int_{0}^{\pi / 2} y d x\), where y = sin x
= \(\int_{0}^{\pi / 2} \sin x d x\)
= \([-\cos x]_{0}^{\pi / 2}\)
= -cos \(\frac{\pi}{2}\) + cos 0
= 0 + 1
= 1 sq unit.
(v) xy = 2, x = 1, x = 4.
Solution:
For xy = 2, y = \(\frac{2}{x}\)
Required area = \(\int_{1}^{4} y d x\), where y = \(\frac{2}{x}\)
= \(\int_{1}^{4} \frac{2}{x} d x\)
= \([2 \log |x|]_{1}^{4}\)
= 2 log 4 – 2 log 1
= 2 log 4 – 0
= 2 log 4 sq units.
(vi) y2 = x, x = 0, x = 4.
Solution:
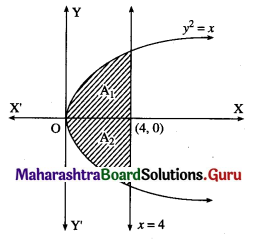
The required area consists of two bounded regions A1 and A2 which are equal in areas.
For y2 = x, y = √x
Required area = A1 + A2 = 2A1

![]()
(vii) y2 = 16x, x = 0, x = 4.
Solution:
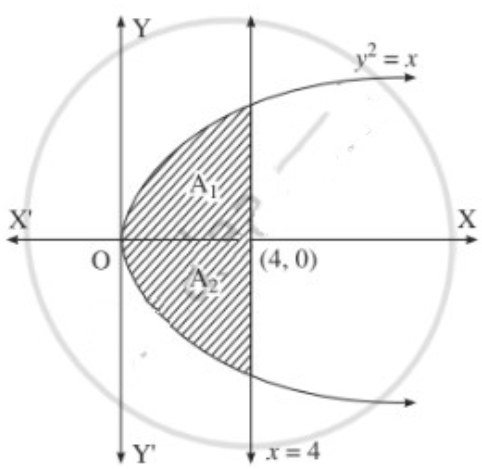
The required area consists of two bounded regions A1 and A2 which are equal in areas.
For y2 = x, y = √x
Required area = A1 + A2 = 2A1
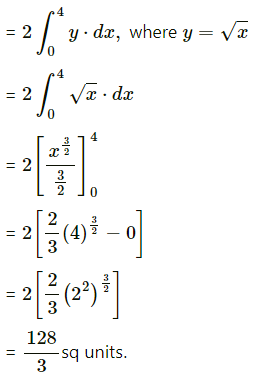
2. Find the area of the region bounded by the parabola:
(i) y2 = 16x and its latus rectum.
Solution:
Comparing y2 = 16x with y2 = 4ax, we get
4a = 16
∴ a = 4
∴ focus is S(a, 0) = (4, 0)
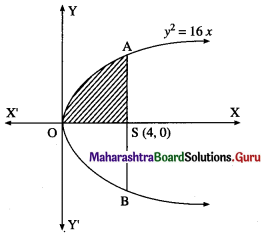
For y2 = 16x, y = 4√x
Required area = area of the region OBSAO
= 2 [area of the region OSAO]
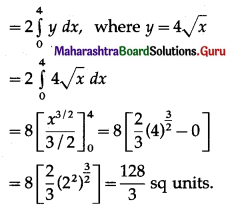
(ii) y = 4 – x2 and the X-axis.
Solution:
The equation of the parabola is y = 4 – x2
∴ x2 = 4 – y
i.e. (x – 0)2 = -(y – 4)
It has vertex at P(0, 4)
For points of intersection of the parabola with X-axis,
we put y = 0 in its equation.
∴ 0 = 4 – x2
∴ x2 = 4
∴ x = ± 2
∴ the parabola intersect the X-axis at A(-2, 0) and B(2, 0)
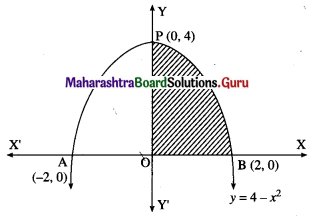
Required area = area of the region APBOA
= 2[area of the region OPBO]

![]()
3. Find the area of the region included between:
(i) y2 = 2x and y = 2x.
Solution:
The vertex of the parabola y2 = 2x is at the origin O = (0, 0).
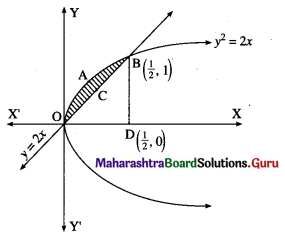
To find the points of intersection of the line and the parabola, equaling the values of 2x from both the equations we get,
y2 = y
∴ y2 – y = 0
∴ y = 0 or y = 1
When y = 0, x = \(\frac{0}{2}\) = 0
When y = 1, x = \(\frac{1}{2}\)
∴ the points of intersection are 0(0, 0) and B(\(\frac{1}{2}\), 1)
Required area = area of the region OABCO = area of the region OABDO – area of the region OCBDO
Now, area of the region OABDO = area under the parabola y2 = 2x between x = 0 and x = \(\frac{1}{2}\)

Area of the region OCBDO = area under the line y = 2x between x = 0 and x = \(\frac{1}{2}\)

(ii) y2 = 4x and y = x.
Solution:
The vertex of the parabola y2 = 4x is at the origin O = (0, 0).
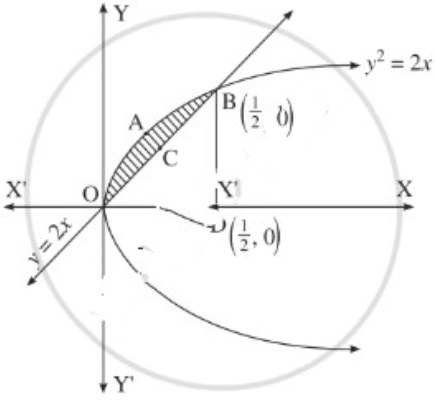
To find the points of intersection of the line and the parabola, equaling the values of 4x from both the equations we get,
∴ y2 = y
∴ y2 – y = 0
∴ y(y – 1) = 0
∴ y = 0 or y = 1
When y = 0, x = \(\frac{0}{2}\) = 0
When y = 1, x = \(\frac{1}{2}\)
∴ the points of intersection are O(0, 0) and B(\(\frac{1}{2}\), 1)
Required area = area of the region OABCO = area of the region OABDO – area of the region OCBDO
Now, area of the region OABDO = area under the parabola y2 = 4x between x = 0 and x = \(\frac{1}{2}\)
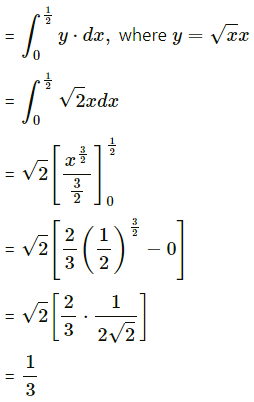
Area of the region OCBDO = area under the line y = 2x between x = 0 and x = \(\frac{1}{2}\)
![]()
(iii) y = x2 and the line y = 4x.
Solution:
The vertex of the parabola y = x2 is at the origin 0(0, 0)
To find the points of the intersection of a line and the parabola.
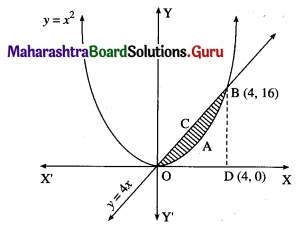
Equating the values of y from the two equations, we get
x2 = 4x
∴ x2 – 4x = 0
∴ x(x – 4) = 0
∴ x = 0, x = 4
When x = 0, y = 4(0) = 0
When x = 4, y = 4(4) = 16
∴ the points of intersection are 0(0, 0) and B(4, 16)
Required area = area of the region OABCO = (area of the region ODBCO) – (area of the region ODBAO)
Now, area of the region ODBCO = area under the line y = 4x between x = 0 and x = 4
= \(\int_{0}^{4} y d x\), where y = 4x
= \(\int_{0}^{4} 4 x d x\)
= 4\(\int_{0}^{4} x d x\)
= 4\([latex]\int_{0}^{4} x d x\)[/latex]
= 2(16 – 0)
= 32
Area of the region ODBAO = area under the parabola y = x2 between x = 0 and x = 4
= \(\int_{0}^{4} y d x\), where y = x2
= \(\int_{0}^{4} x^{2} d x\)
= \(\left[\frac{x^{3}}{3}\right]_{0}^{4}\)
= \(\frac{1}{3}\) (64 – 0)
= \(\frac{64}{3}\)
∴ required area = 32 – \(\frac{64}{3}\) = \(\frac{32}{3}\) sq units.
(iv) y2 = 4ax and y = x.
Solution:
The vertex of the parabola y2 = 4ax is at the origin O = (0, 0).
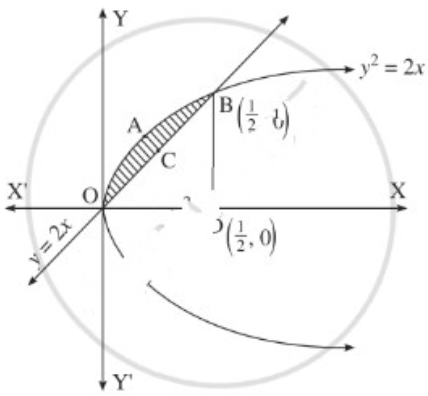
To find the points of intersection of the line and the parabola, equaling the values of 4ax from both the equations we get,
∴ y2 = y
∴ y2 – y = 0
∴ y(y – 1) = 0
∴ y = 0 or y = 1
When y = 0, x = \(\frac{0}{2}\) = 0
When y = 1, x = \(\frac{1}{2}\)
∴ the points of intersection are O(0, 0) and B(\(\frac{1}{2}\), 1)
Required area = area of the region OABCO = area of the region OABDO – area of the region OCBDO
Now, area of the region OABDO
= area under the parabola y2 = 4ax between x = 0 and x = \(\frac{1}{2}\)
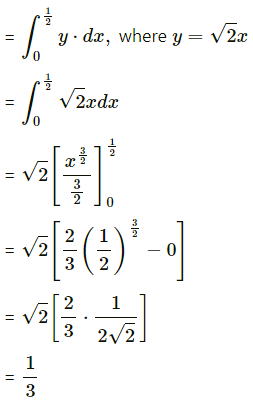
Area of the region OCBDO
= area under the line y
= 4ax between x = 0 and x = \(\frac{1}{4 a x}\)
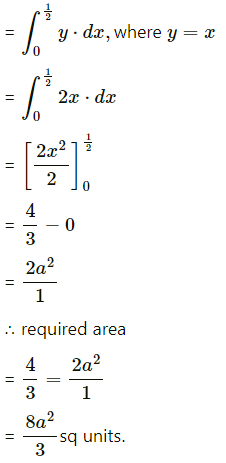
![]()
(v) y = x2 + 3 and y = x + 3.
Solution:
The given parabola is y = x2 + 3, i.e. (x – 0)2 = y – 3
∴ its vertex is P(0, 3).
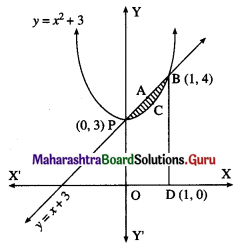
To find the points of intersection of the line and the parabola.
Equating the values of y from both the equations, we get
x2 + 3 = x + 3
∴ x2 – x = 0
∴ x(x – 1) = 0
∴ x = 0 or x = 1
When x = 0, y = 0 + 3 = 3
When x = 1, y = 1 + 3 = 4
∴ the points of intersection are P(0, 3) and B(1, 4)
Required area = area of the region PABCP = area of the region OPABDO – area of the region OPCBDO
Now, area of the region OPABDO
= area under the line y = x + 3 between x = 0 and x = 1
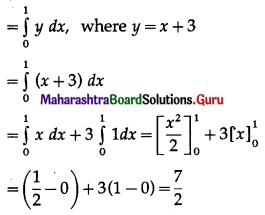
Area of the region OPCBDO = area under the parabola y = x2 + 3 between x = 0 and x = 1
