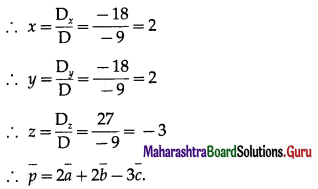Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Vectors Ex 5.1 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 5 Vectors Ex 5.1
Question 1.
The vector \(\bar{a}\) is directed due north and \(|\bar{a}|\) = 24. The vector \(\bar{b}\) is directed due west and \(|\bar{b}|\) = 7. Find \(|\bar{a}+\bar{b}|\).
Solution:
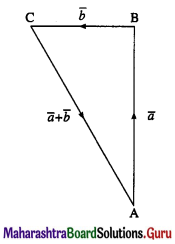
Let \(\overline{\mathrm{AB}}\) = \(\bar{a}\), \(\overline{\mathrm{BC}}\) = \(\bar{b}\)
Then \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{AB}}\) + \(\overline{\mathrm{BC}}\) = a + b
Given : \(|\bar{a}|\) = \(|\overline{\mathrm{AB}}|\) = l(AB) = 24 and
\(|\bar{b}|\) = \(|\overline{\mathrm{BC}}|\) = l(BC) = 7
∴ ∠ABC = 90°
∴ [l(AC)]2 = [l(AB)]2 + [l(BC)]2
= (24)2 + (7)2 = 625
∴ l(AC) = 25 ∴ \(|\overline{\mathrm{AC}}|\) = 25
∴ \(|\bar{a}+\bar{b}|\) = \(|\overline{\mathrm{AC}}|\) = 25.
Question 2.
In the triangle PQR, \(\overline{\mathrm{PQ}}\) = 2\(\bar{a}\) and \(\overline{\mathrm{QR}}\) = 2\(\bar{b}\). The mid-point of PR is M. Find following vectors in terms of \(\bar{a}\) and \(\bar{b}\).
(i) \(\overline{\mathrm{PR}}\)
Solution:
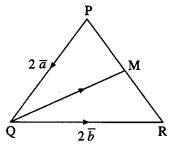
Given : \(\overline{\mathrm{PQ}}\) = 2\(\bar{a}\), \(\overline{\mathrm{QR}}\) = 2\(\bar{b}\)
(i) \(\overline{\mathrm{PR}}\) = \(\overline{\mathrm{PQ}}\) + \(\overline{\mathrm{QR}}\)
= 2\(\bar{a}\) + 2\(\bar{a}\).
![]()
(ii) \(\overline{\mathrm{PM}}\)
Solution:
∵ M is the midpoint of PR
∴ \(\overline{\mathrm{PM}}\) = \(\frac{1}{2} \overline{\mathrm{PR}}\) = \(\frac{1}{2}\)[2\(\bar{a}\) + 2\(\bar{b}\)]
= \(\bar{a}\) + \(\bar{b}\).
(iii) \(\overline{\mathrm{QM}}\)
Solution:
\(\overline{\mathrm{RM}}\) = \(\frac{1}{2}(\overline{\mathrm{RP}})\) = \(-\frac{1}{2} \overline{\mathrm{PR}}\) = \(-\frac{1}{2}\)(2\(\bar{a}\) + 2\(\bar{b}\))
= –\(\bar{a}\) – \(\bar{b}\)
∴ \(\overline{\mathrm{QM}}\) = \(\overline{\mathrm{QR}}\) + \(\overline{\mathrm{RM}}\)
= 2\(\bar{b}\) – \(\bar{a}\) – \(\bar{b}\)
= \(\bar{b}\) – \(\bar{a}\).
Question 3.
OABCDE is a regular hexagon. The points A and B have position vectors \(\bar{a}\) and \(\bar{b}\) respectively, referred to the origin O. Find, in terms of \(\bar{a}\) and \(\bar{b}\) the position vectors of C, D and E.
Solution:
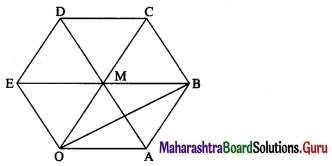
Given : \(\overline{\mathrm{OA}}\) = \(\bar{a}\), \(\overline{\mathrm{OB}}\) = \(\bar{a}\) Let AD, BE, OC meet at M.
Then M bisects AD, BE, OC.
\(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{AO}}\) + \(\overline{\mathrm{OB}}\) = –\(\overline{\mathrm{OA}}\) + \(\overline{\mathrm{OB}}\) = –\(\bar{a}\) + \(\bar{b}\) = \(\bar{b}\) – \(\bar{a}\)
∵ OABM is a parallelogram

Hence, the position vectors of C, D and E are 2\(\bar{b}\) – 2\(\bar{a}\), 2\(\bar{b}\) – 3\(\bar{a}\) and \(\bar{b}\) – 2\(\bar{a}\) respectively.
![]()
Question 4.
If ABCDEF is a regular hexagon, show that \(\overline{\mathrm{AB}}\) + \(\overline{\mathrm{AC}}\) + \(\overline{\mathrm{AD}}\) + \(\overline{\mathrm{AE}}\) + \(\overline{\mathrm{AF}}\) = 6\(\overline{\mathrm{AO}}\), where O is the center of the hexagon.
Solution:
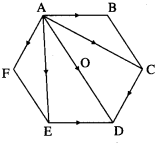
ABCDEF is a regular hexagon.
∴ \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{ED}}\) and \(\overline{\mathrm{AF}}\) = \(\overline{\mathrm{CD}}\)
∴ by the triangle law of addition of vectors,
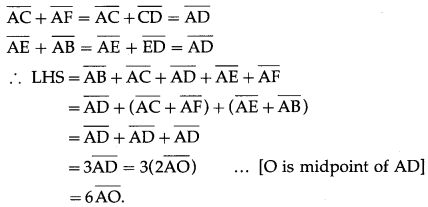
Question 5.
Check whether the vectors \(2 \hat{i}+2 \hat{j}+3 \hat{k}\), + \(-3 \hat{i}+3 \hat{j}+2 \hat{k}\), + \(3 \hat{i}+4 \hat{k}\) form a triangle or not.
Solution:
Let, if possible, the three vectors form a triangle ABC
with \(\overline{A B}\) = \(2 \hat{i}+2 \hat{j}+3 \hat{k}\), \(\overline{B C}\) = \(3 \hat{i}+3 \hat{j}+2 \hat{k}\), \(\overline{A C}\) = \(3 \hat{i}+4 \hat{k}\)
Now, \(\overline{A B}\) + \(\overline{B C}\)
= \((2 \hat{i}+2 \hat{j}+3 \hat{k})\) + \((-3 \hat{i}+3 \hat{j}+2 \hat{k})\)
= \(-\hat{i}+5 \hat{j}+5 \hat{k} \neq 3 \hat{i}+4 \hat{k}\) = \(\overline{\mathrm{AC}}\)
Hence, the three vectors do not form a triangle.
![]()
Question 6.
In the figure 5.34 express \(\bar{c}\) and \(\bar{d}\) in terms of \(\bar{a}\) and \(\bar{b}\). Find a vector in the direction of \(\bar{a}\) = \(\hat{i}-2 \hat{j}\) that has magnitude 7 units.
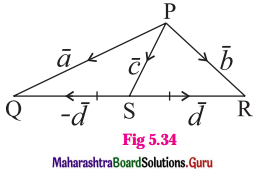
Solution:
\(\overline{\mathrm{PQ}}\) = \(\overline{\mathrm{PS}}\) + \(\overline{\mathrm{SQ}}\)
∴ \(\bar{a}\) = \(\bar{c}\) – \(\bar{d}\) … (1)
\(\overline{\mathrm{PR}}\) = \(\overline{\mathrm{PS}}\) + \(\overline{\mathrm{SR}}\)
∴ \(\bar{b}\) = \(\bar{c}\) + \(\bar{d}\) … (2)
Adding equations (1) and (2), we get
\(\bar{a}\) + \(\bar{b}\) = (\(\bar{c}\) – \(\bar{d}\)) + (\(\bar{c}\) + \(\bar{d}\)) = 2\(\bar{c}\)
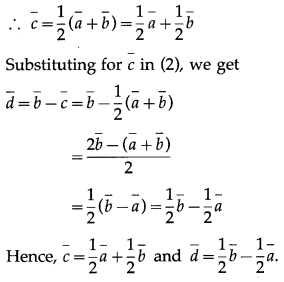
Question 7.
Find the distance from (4, -2, 6) to each of the following :
(a) The XY-plane
Solution:
Let the point A be (4, -2, 6).
Then,
The distance of A from XY-plane = |z| = 6
(b) The YZ-plane
Solution:
The distance of A from YZ-plane = |x| = 4
![]()
(c) The XZ-plane
Solution:
The distance of A from ZX-plane = |y| = 2
(d) The X-axis
Solution:
The distance of A from X-axis
= \(\sqrt{y^{2}+z^{2}}\) = \(\sqrt{(-2)^{2}+6^{2}}\) = \(\sqrt{40}\) = \(2 \sqrt{10}\)
(e) The Y-axis
Solution:
The distance of A from Y-axis
= \(\sqrt{z^{2}+x^{2}}\) = \(\sqrt{6^{2}+4^{2}}\) = \(\sqrt{52}\) = \(2 \sqrt{13}\)
(f) The Z-axis
Solution:
The distance of A from Z-axis
= \(\sqrt{x^{2}+y^{2}}\) = \(\sqrt{4^{2}+(-2)^{2}}\) = \(\sqrt{20}\) = \(2 \sqrt{5}\)
![]()
Question 8.
Find the coordinates of the point which is located :
(a) Three units behind the YZ-plane, four units to the right of the XZ-plane and five units above the XY-plane.
Solution:
Let the coordinates of the point be (x, y, z).
Since the point is located 3 units behind the YZ- j plane, 4 units to the right of XZ-plane and 5 units , above the XY-plane,
x = -3, y = 4 and z = 5
Hence, coordinates of the required point are (-3, 4, 5)
(b) In the YZ-plane, one unit to the right of the XZ-plane and six units above the XY-plane.
Solution:
Let the coordinates of the point be (x, y, z).
Since the point is located in the YZ plane, x = 0. Also, the point is one unit to the right of XZ-plane and six units above the XY-plane.
∴ y = 1, z = 6.
Hence, coordinates of the required point are (0, 1, 6).
Question 9.
Find the area of the triangle with vertices (1, 1, 0), (1, 0, 1) and (0, 1, 1).
Solution:
Let A = (1, 1, 0), B = (1, 0, 1), C = (0, 1, 1)

![]()
Question 10.
If \(\overline{\mathrm{AB}}\) = \(2 \hat{i}-4 \hat{j}+7 \hat{k}\) and initial point A ≡ (1, 5, ,0). Find the terminal point B.
Solution:
Let \(\bar{a}\) and \(\bar{b}\) be the position vectors of A and B.
Given : A = (1, 5, 0) .’. \(\bar{a}\) = \(\hat{i}+5 \hat{j}\)
Now, \(\overline{\mathrm{AB}}\) = \(2 \hat{i}-4 \hat{j}+7 \hat{k}\)
∴ \(\bar{b}\) – \(\bar{a}\) = \(2 \hat{i}-4 \hat{j}+7 \hat{k}\)
∴ \(\bar{b}\) = \((2 \hat{i}-4 \hat{j}+7 \hat{k})\) + \(\bar{a}\)
= \((2 \hat{i}-4 \hat{j}+7 \hat{k})\) + \((\hat{i}+5 \hat{j})\)
= \(3 \hat{i}+\hat{j}+7 \hat{k}\)
Hence, the terminal point B = (3, 1, 7).
Question 11.
Show that the following points are collinear :
(i) A (3, 2, -4), B (9, 8, -10), C (-2, -3, 1).
Solution:
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) be the position vectors of the points.
A = (3, 2, -4), B = (9, 8, -10) and C = (-2, -3, 1) respectively.

∴ \(\overline{\mathrm{BC}}\) is a non-zero scalar multiple of \(\overline{\mathrm{AB}}\)
∴ they are parallel to each other.
But they have the point B in common.
∴ \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{AB}}\) are collinear vectors.
Hence, the points A, B and C are collinear.
(ii) P (4, 5, 2), Q (3, 2, 4), R (5, 8, 0).
Solution:
Let \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) be the position vectors of the points.
P = (4, 5, 2), Q = (3, 2, 4), R = (5, 8, 0) respectively.
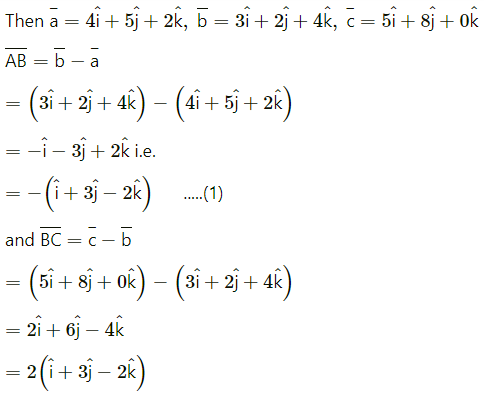
= 2.\(\overline{\mathrm{AB}}\) …[By (1)]
∴ \(\overline{\mathrm{BC}}\) is a non-zero scalar multiple of \(\overline{\mathrm{AB}}\)
∴ they are parallel to each other.
But they have the point B in common.
∴ \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{AB}}\) are collinear vectors.
Hence, the points A, B and C are collinear.
![]()
Question 12.
If the vectors \(2 \hat{i}-q \hat{j}+3 \hat{k}\) and \(4 \hat{i}-5 \hat{j}+6 \hat{k}\) are collinear, then find the value of q.
Solution:
The vectors \(2 \hat{i}-q \hat{j}+3 \hat{k}\) and \(4 \hat{i}-5 \hat{j}+6 \hat{k}\) are collinear
∴ the coefficients of \(\hat{i}, \hat{j}, \hat{k}\) are proportional
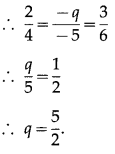
Question 13.
Are the four points A(1, -1, 1), B(-1, 1, 1), C(1, 1, 1) and D(2, -3, 4) coplanar? Justify your answer.
Solution:
The position vectors \(\bar{a}\), \(\bar{b}\), \(\bar{c}\), \(\bar{d}\) of the points A, B, C, D are
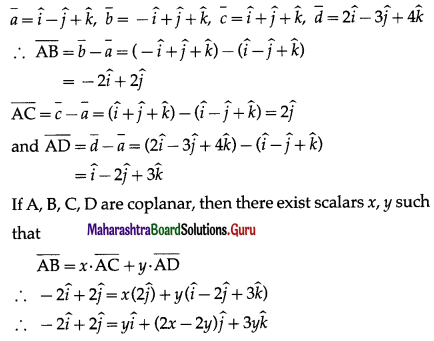
By equality of vectors,
y = -2 ….(1)
2x – 2y = 2 … (2)
3y = 0 … (3)
From (1), y = -2
From (3), y = 0 This is not possible.
Hence, the points A, B, C, D are not coplanar.
![]()
Question 14.
Express \(-\hat{i}-3 \hat{j}+4 \hat{k}\) as linear combination of the vectors \(2 \hat{i}+\hat{j}-4 \hat{k}\), \(2 \hat{i}-\hat{j}+3 \hat{k}\) and \(3 \hat{i}+\hat{j}-2 \hat{k}\).
Solution:
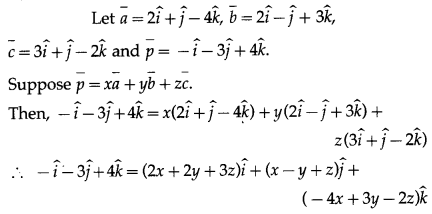
By equality of vectors,
2x + 2y + 3 = -1
x – y + z = -3
-4x + 3y – 2z = 4
We have to solve these equations by using Cramer’s Rule
D = \(\left|\begin{array}{rrr}
2 & 2 & 3 \\
1 & -1 & 1 \\
-4 & 3 & -2
\end{array}\right|\)
= 2(2 – 3) – 2(-2 + 4) + 3(3 – 4)
= -2 – 4 – 3 = -9 ≠ 0
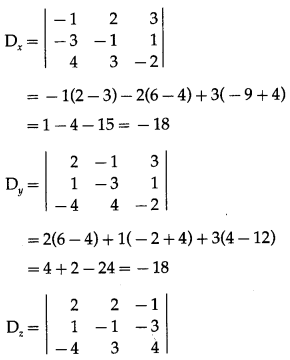
= 2(-4 + 9) – 2(4 – 12) – 1(3 – 4)
= 10 + 16 + 1 = 27