Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.1 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 6 Differential Equations Ex 6.1
1. Determine the order and degree of each of the following differential equations:
Question (i).
\(\frac{d y}{d x^{2}}+X\left(\frac{d y}{d x}\right)+y=2 \sin x\)
Solution:
The given D.E. is \(\frac{d y}{d x^{2}}+X\left(\frac{d y}{d x}\right)+y=2 \sin x\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. is of order 2 and degree 1.
![]()
Question (ii).
\(\sqrt[3]{1+\left(\frac{d y}{d x}\right)^{2}}=\frac{d^{2} y}{d x^{2}}\)
Solution:
The given D.E. is \(\sqrt[3]{1+\left(\frac{d y}{d x}\right)^{2}}=\frac{d^{2} y}{d x^{2}}\)
On cubing both sides, we get
\(1+\left(\frac{d y}{d x}\right)^{2}=\left(\frac{d^{2} y}{d x^{2}}\right)^{3}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 3.
∴ the given D.E. is of order 2 and degree 3.
Question (iii).
\(\frac{d y}{d x}=\frac{2 \sin x+3}{\frac{d y}{d x}}\)
Solution:
The given D.E. is \(\frac{d y}{d x}=\frac{2 \sin x+3}{\frac{d y}{d x}}\)
∴ \(\left(\frac{d y}{d x}\right)^{2}\) = 2 sin x + 3
This D.E. has highest order derivative \(\frac{d y}{d x}\) with power 2.
∴ the given D.E. is of order 1 and degree 2.
Question (iv).
\(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}+x=\sqrt{1+\frac{d^{3} y}{d x^{3}}}\)
Solution:
The given D.E. is \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}+x=\sqrt{1+\frac{d^{3} y}{d x^{3}}}\)
On squaring both sides, we get
\(\left(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}+x\right)^{2}=1+\frac{d^{3} y}{d x^{3}}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 1.
∴ the given D.E. has order 3 and degree 1.
![]()
Question (v).
\(\frac{d^{2} y}{d t^{2}}+\left(\frac{d y}{d t}\right)^{2}+7 x+5=0\)
Solution:
The given D.E. is \(\frac{d^{2} y}{d t^{2}}+\left(\frac{d y}{d t}\right)^{2}+7 x+5=0\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. has order 2 and degree 1.
Question (vi).
(y”‘)2 + 3y” + 3xy’ + 5y = 0
Solution:
The given D.E. is (y”‘)2 + 3y” + 3xy’ + 5y = 0
This can be written as:
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}+3 \frac{d^{2} y}{d x^{2}}+3 x \frac{d y}{d x}+5 y=0\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 2.
∴ The given D.E. has order 3 and degree 2.
Question (vii).
\(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\cos \left(\frac{d y}{d x}\right)=0\)
Solution:
The given D.E. is \(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\cos \left(\frac{d y}{d x}\right)=0\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\)
∴ order = 2
Since this D.E. cannot be expressed as a polynomial in differential coefficients, the degree is not defined.
![]()
Question (viii).
\(\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{\frac{3}{2}}=8 \frac{d^{2} y}{d x^{2}}\)
Solution:
The given D.E. is \(\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{\frac{3}{2}}=8 \frac{d^{2} y}{d x^{2}}\)
On squaring both sides, we get
\(\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{3}=8^{2} \cdot\left(\frac{d^{2} y}{d x^{2}}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 2.
∴ the given D.E. has order 2 and degree 2.
Question (ix).
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{\frac{1}{2}} \cdot\left(\frac{d y}{d x}\right)^{\frac{1}{3}}=20\)
Solution:
The given D.E. is \(\left(\frac{d^{3} y}{d x^{3}}\right)^{\frac{1}{2}} \cdot\left(\frac{d y}{d x}\right)^{\frac{1}{3}}=20\)
∴ \(\left(\frac{d^{3} y}{d x^{3}}\right)^{3} \cdot\left(\frac{d y}{d x}\right)^{2}=20^{6}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 3.
∴ the given D.E. has order 3 and degree 3.
![]()
Question (x).
\(x+\frac{d^{2} y}{d x^{2}}=\sqrt{1+\left(\frac{d^{2} y}{d x^{2}}\right)^{2}}\)
Solution:
The given D.E. is \(x+\frac{d^{2} y}{d x^{2}}=\sqrt{1+\left(\frac{d^{2} y}{d x^{2}}\right)^{2}}\)
On squaring both sides, we get
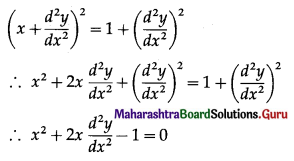
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. has order 2 and degree 1.