Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Line and Plane Ex 6.4 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 6 Line and Plane Ex 6.4
Question 1.
Find the angle between planes \(\bar{r} \cdot(\hat{i}+\hat{j}+2 \hat{k})\) = 13 and \(\bar{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})\) = 31 .
Solution:
The acute angle θ between the planes \(\bar{r} \cdot \bar{n}_{1}\) = d1 and \(\bar{r} \cdot \bar{n}_{2}\) = d2 is given by

Question 2.
Find the acute angle between the line \(\bar{r} \cdot(\hat{i}+2 \hat{j}+2 \hat{k})+\lambda(2 \hat{i}+3 \hat{j}-6 \hat{k})\) and the plane \(\bar{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})\) = 0
Solution:
The acute angle θ between the line \(\bar{r}=\bar{a}+\lambda \bar{b}\) and the plane \(\bar{r} \cdot \bar{n}\) = d is given by
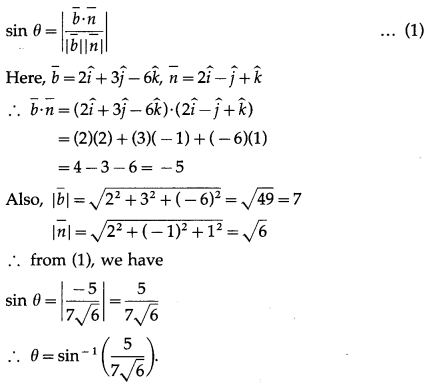
![]()
Question 3.
Show that lines \(\bar{r}=(2 \hat{j}-3 \hat{k})+\lambda(\hat{i}+2 \hat{j}+3 \hat{k})\) and \(\bar{r}=(2 \hat{i}+6 \hat{j}+3 \hat{k})+\mu(2 \hat{i}+3 \hat{j}+4 \hat{k})\) are coplanar. Find the equation of the plane determined by them.
Solution:
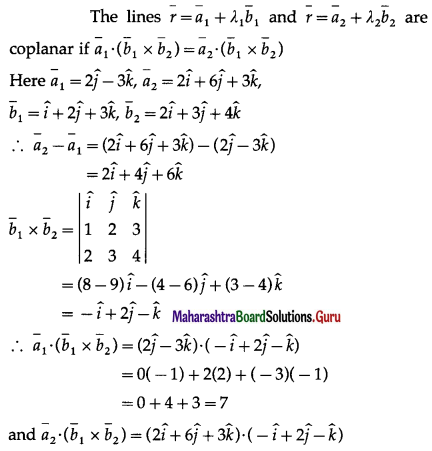
= 2(-1) + 6(2) + 3(-1)
= -2 + 12 – 3 = 7
∴ \(\bar{a}_{1} \cdot\left(\bar{b}_{1} \times \bar{b}_{2}\right)=\bar{a}_{2} \cdot\left(\bar{b}_{1} \times \bar{b}_{2}\right)\)
Hence, the given lines are coplanar.
The plane determined by these lines is given by
∴ \(\bar{r} \cdot\left(\overline{b_{1}} \times \overline{b_{2}}\right)=\overline{a_{1}} \cdot\left(\overline{b_{1}} \times \overline{b_{2}}\right)\)
i.e. \(\bar{r} \cdot(-\hat{i}+2 \hat{j}-\hat{k})\)
Hence, the given lines are coplanar and the equation of the plane determined by these lines is
\(\bar{r} \cdot(-\hat{i}+2 \hat{j}-\hat{k})\) = 7
Question 4.
Find the distance of the point \(4 \hat{i}-3 \hat{j}+\hat{k}\) from the plane \(\bar{r} \cdot(2 \hat{i}+3 \hat{j}-6 \hat{k})\) = 21 .
Solution:
The distance of the point A(\(\bar{a}\)) from the plane \(\bar{r} \cdot \bar{n}=p\) is given by d = \(\frac{|\bar{a} \cdot \bar{n}-p|}{|n|}\) …(1)
Here, \(\bar{a}=4 \hat{i}-3 \hat{j}+\hat{k}\), \(\bar{n}=2 \hat{i}+3 \hat{j}-6 \hat{k}\), p = 21
∴ \(\bar{a} \cdot \bar{n}\) = \((4 \hat{i}-3 \hat{j}+\hat{k}) \cdot(2 \hat{i}+3 \hat{j}-6 \hat{k})\)
= (4)(2) + (-3)(3) + (1)(-6)
= 8 – 9 – 6 = -7
Also, \(\sqrt{2^{2}+3^{2}+(-6)^{2}}=\sqrt{49}\) = 7
∴ from (1), the required distance
= \(\frac{|-7-21|}{7}\) = 4units
![]()
Question 5.
Find the distance of the point (1, 1, -1) from the plane 3x + 4y – 12z + 20 = 0.
Solution:
The distance of the point (x1, y1, z1) from the plane ax + by + cz + d = 0 is \(\left|\frac{a x_{1}+b y_{1}+c z_{1}+d}{\sqrt{a^{2}+b^{2}+c^{2}}}\right|\)
∴ the distance of the point (1, 1, -1) from the plane 3x + 4y – 12z + 20 = 0 is \(\left|\frac{3(1)+4(1)-12(-1)+20}{\sqrt{3^{2}+4^{2}+(-12)^{2}}}\right|\)
= \(\left|\frac{3+4+12+20}{\sqrt{9+16+144}}\right|=\frac{39}{\sqrt{169}}\)
= \(\frac{39}{13}\) = 3units