Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Line and Plane Miscellaneous Exercise 6A Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 6 Line and Plane Miscellaneous Exercise 6A
Question 1.
Find the vector equation of the line passing through the point having position vector \(3 \hat{i}+4 \hat{j}-7 \hat{k}\) and parallel to \(6 \hat{i}-\hat{j}+\hat{k}\).
Solution:
The vector equation of the line passing through A(\(\bar{a}\)) and parallel to the vector \(\bar{b}\) is \(\overline{\mathrm{r}}=\overline{\mathrm{a}}+\lambda \overline{\mathrm{b}}\), where λ is a scalar.
∴ the vector equation of the line passing through the point having position vector
\(3 \hat{i}+4 \hat{j}-7 \hat{k}\) and parallel to the vector \(6 \hat{i}-\hat{j}+\hat{k}\) is
\(\overline{\mathrm{r}}=(3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}-7 \hat{\mathrm{k}})+\lambda(\hat{6 \hat{\mathrm{i}}}-\hat{\mathrm{j}}+\hat{\mathrm{k}})\).
Question 2.
Find the vector equation of the line which passes through the point (3, 2, 1) and is parallel to the vector \(2 \hat{i}+2 \hat{j}-3 \hat{k}\).
Solution:
The vector equation of the line passing through A(\(\bar{a}\)) and parallel to the vector \(\bar{b}\) is \(\overline{\mathrm{r}}=\overline{\mathrm{a}}+\lambda \overline{\mathrm{b}}\), where λ is a scalar.
∴ the vector equation of the line passing through the point having position vector \(3 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}}\) and parallel to the vector
\(2 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}-3 \hat{\mathrm{k}} \text { is } \overline{\mathrm{r}}=(3 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}})+\lambda(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-3 \hat{\mathrm{k}})\)
Question 3.
Find the Cartesian equations of the line which passes through the point (-2, 4, -5) and parallel to the line \(\frac{x+2}{3}=\frac{y-3}{5}=\frac{z+5}{6}\)
Solution:
The line \(\frac{x+2}{3}=\frac{y-3}{5}=\frac{z+5}{6}\) has direction ratios 3, 5, 6. The required line has direction ratios 3, 5, 6 as it is parallel to the given line.
It passes through the point (-2, 4, -5).
The cartesian equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are

![]()
Question 4.
Obtain the vector equation of the line \(\frac{x+5}{3}=\frac{y+4}{5}=\frac{z+5}{6}\).
Solution:
The cartesian equations of the line are \(\frac{x+5}{3}=\frac{y+4}{5}=\frac{z+5}{6}\).
This line is passing through the point A(-5, -4, -5) and having direction ratios 3, 5, 6.
Let \(\bar{a}\) be the position vector of the point A w.r.t. the origin and \(\bar{b}\) be the vector parallel to the line.
Then \(\bar{a}=-5 \hat{i}-4 \hat{j}-5 \hat{k}\) and \(\bar{b}=3 \hat{i}+5 \hat{j}+6 \hat{k}\).
The vector equation of the line passing through A(\(\bar{a}\)) and parallel to \(\bar{b}\) is \(\bar{r}=\bar{a}+\lambda \bar{b}\) where λ is a scalar.
∴ the vector equation of the required line is \(\bar{r}=(-5 \hat{i}-4 \hat{j}-6 \hat{k})+\lambda(3 \hat{i}+5 \hat{j}+6 \hat{k})\)
Question 5.
Find the vector equation of the line which passes through the origin and the point (5, -2, 3).
Solution:
Let \(\bar{b}\) be the position vector of the point B(5, -2, 3).
Then \(\bar{b}=5 \hat{i}-2 \hat{j}+3 \hat{k}\)
Origin has position vector \(\overline{0}=0 \hat{i}+0 \hat{j}+0 \hat{k}\).
The vector equation the line passing through A(\(\bar{a}\)) and B(\(\bar{b}\)) is \(\bar{r}=\bar{a}+\lambda(\bar{b}-\bar{a})\) where λ is a scalar.
∴ the vector equation of the required line is \(\bar{r}=\overline{0}+\lambda(\bar{b}-\overline{0})=\lambda(5 \hat{i}-2 \hat{j}+3 \hat{k})\)
Question 6.
Find the Cartesian equations of the line which passes through points (3, -2, -5) and (3, -2, 6).
Solution:
Let A = (3, -2, -5), B = (3, -2, 6)
The direction ratios of the line AB are
3 – 3, -2 – (-2), 6 – (-5) i.e. 0, 0, 11.
The parametric equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are
x = x1 + aλ, y = y1 + bλ, z = z1 + cλ
∴ the parametric equattions of the line passing through (3, -2, -5) and having direction ratios are 0, 0, 11 are
x = 3 + (0)λ, y = -2 + 0(λ), z = -5 + 11λ
i.e. x = 3, y = -2, z = 11λ – 5
∴ the cartesian equations of the line are
x = 3, y = -2, z = 11λ – 5, λ is a scalar.
![]()
Question 7.
Find the Cartesian equations of the line passing through A(3, 2, 1) and B(1, 3, 1).
Solution:
The direction ratios of the line AB are 3 – 1, 2 – 3, 1 – 1 i.e. 2, -1, 0.
The parametric equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are
x = x1 + aλ, y = y1 + bλ, z = z1 + cλ
∴ the parametric equattions of the line passing through (3, 2, 1) and having direction ratios 2, -1, 0 are
x = 3 + 2λ, y = 2 – λ, z = 1 + 0(λ)
x – 3 = 2λ, y – 2 = -λ, z = 1
∴ \(\frac{x-3}{2}=\frac{y-2}{-1}\) = λ, z = 1
∴ the cartesian equations of the line are
\(\frac{x-3}{2}=\frac{y-2}{-1}\), z = 1.
Question 8.
Find the Cartesian equations of the line passing through the point A(1, 1, 2) and perpendicular to vectors \(\bar{b}=\hat{i}+2 \hat{j}+\hat{k}\) and \(\bar{c}=3 \hat{i}+2 \hat{j}-\hat{k}\).
Solution:
Let the required line have direction ratios p, q, r. ,
It is perpendicular to the vectors \(\bar{b}=\hat{i}+2 \hat{j}+\hat{k}\) and \(\bar{c}=3 \hat{i}+2 \hat{j}-\hat{k}\).
∴ it is perpendicular to lines whose direction ratios are 1, 2, 1 and 3, 2, -1.
∴ p + 2q + r = 0, 3p + 2q – r = 0
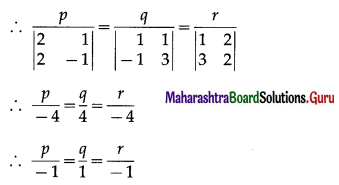
∴ the required line has direction ratios -1, 1, -1.
The cartesian equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are
\(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)
∴ the cartesian equations of the line passing through the point (1, 1, 2) and having direction ratios -1, 1, -1 are
\(\frac{x-1}{-1}=\frac{y-1}{1}=\frac{z-2}{-1}\)
Question 9.
Find the Cartesian equations of the line which passes through the point (2, 1, 3) and perpendicular
to lines \(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{3}\) and \(\frac{x}{-3}=\frac{y}{2}=\frac{z}{5}\).
Solution:
Let the required line have direction ratios p, q, r.
It is perpendicular to the vector \(\bar{b}=\hat{i}+2 \hat{j}+\hat{k}\) and \(\bar{c}=3 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}}\).
∴ it is perpendicular to lines whose direction ratios are 1, 2, 1 and 3, 2, -1.
∴ p + 2q + r = 0, 3 + 2q – r = 0
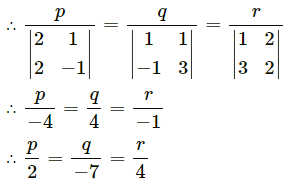
∴ the required line has direction ratios 2, -7, 4.
The cartesian equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are
\(\frac{x=x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)
∴ the cartesian equation of the line passing through the point (2, -7, 4) and having directions ratios 2, -7, 4 are
\(\frac{x-2}{2}=\frac{y-1}{-7}=\frac{z-2}{4}\)
![]()
Question 10.
Find the vector equation of the line which passes through the origin and intersect the line x – 1 = y – 2 = z – 3 at right angle.
Solution:
The given line is \(\frac{x-1}{1}=\frac{y-2}{1}=\frac{z-3}{1}\) = λ … (Say)
∴ coordinates of any point on the line are
x = λ + 1, y = λ + 2, z = λ + 3
∴ position vector of any point on the line is
(λ + 1)\(\hat{i}\) + (λ + 2)\(\hat{j}\) + (λ + 3)\(\hat{k}\) … (1)
If \(\bar{b}\) is parallel to the given line whose direction ratios are 1, 1, 1, then \(\bar{b}=\hat{i}+\hat{j}+\hat{k}\).
Let the required line passing through O meet the given line at M.
∴ position vector of M
= \(\bar{m}\) = (λ + 1)\(\hat{i}\) + (λ + 2)\(\hat{j}\) + (λ + 3)\(\hat{k}\) … [By (1)]
The required line is perpendicular to given line
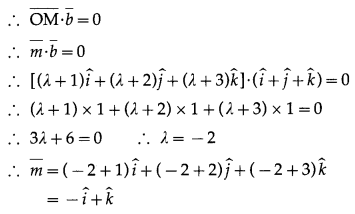
The vector equation of the line passing through A(\(\bar{a}\)) and B(\(\bar{b}\)) is \(\bar{r}=\bar{a}+\lambda(\bar{b}-\bar{a})\), λ is a scalar.
∴ the vector equation of the line passing through o(\(\bar{o}\)) and M(\(\bar{m}\)) is
\(\bar{r}=\overline{0}+\lambda(\bar{m}-\overline{0})=\lambda \bar{m}=\lambda(-\hat{i}+\hat{k})\) where λ is a scalar.
Hence, vector equation of the required line is \(\).
Question 11.
Find the value of λ so that lines \(\frac{1-x}{3}=\frac{7 y-14}{2 \lambda}=\frac{z-3}{2}\) and \(\frac{7-7 x}{3 \lambda}=\frac{y-5}{1}=\frac{6-z}{5}\) are at right angle.
Solution:
The equations of the given lines are


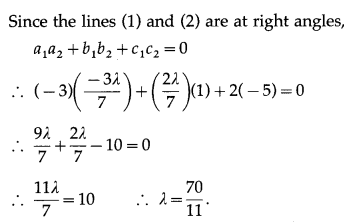
Question 12.
Find the acute angle between lines \(\frac{x-1}{1}=\frac{y-2}{-1}=\frac{z-3}{2}\) and \(\frac{x-1}{2}=\frac{y-2}{1}=\frac{z-3}{1}\).
Solution:

![]()
Question 13.
Find the acute angle between lines x = y, z = 0 and x = 0, z = 0.
Solution:
The equations x = y, z = 0 can be written as \(\frac{x}{1}=\frac{y}{1}\), z = 0
∴ the direction ratios of the line are 1, 1, 0.
The direction ratios of the line x = 0, z = 0, i.e., Y-axis J are 0, 1, 0.
∴ its directiton ratios are 0, 1, 0.
Let \(\bar{a}\) and \(\bar{b}\) be the vectors in the direction of the lines x = y, z = 0 and x = 0, z = 0.
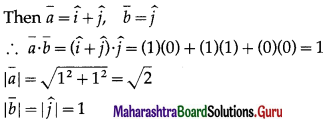
If θ is the acute angle between the lines, then
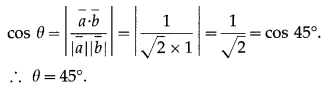
Question 14.
Find the acute angle between lines x = -y, z = 0 and x = 0, z = 0.
Solution:
The equations x = -y, z = 0 can be written as \(\frac{x}{1}=\frac{y}{1}\), z = 0.
∴ the direction ratios of the line are 1, 1, 0.
The direction ratios of the line x = 0, z = 0, i.e., Y-axis are 0, 1, 0.
∴ its direction ratios are 0, 1, 0.
Let \(\bar{a}\) and \(\bar{b}\) be the vectors in the direction of the lines x = y, z = 0 and x = 0, z = 0
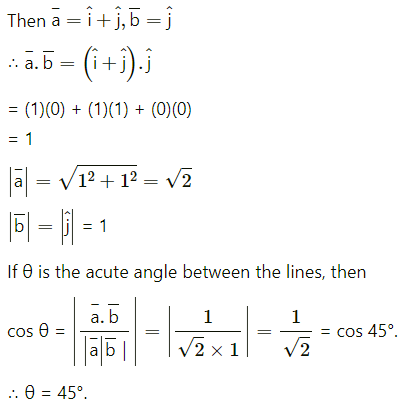
Question 15.
Find the co-ordinates of the foot of the perpendicular drawn from the point (0, 2, 3) to the line \(\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3}\).
Solution:
Let P = (0, 2, 3)
Let M be the foot of the perpendicular drawn from P to the line \(\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3}\) = λ ……(Say)
The coordinates of any point on the line are given by
x = 5λ – 3, y = 2λ + 1, z = 3λ – 4
Let M = (5λ – 3, 2λ + 1, 3λ – 4) …(1)
The direction ratios of PM are
5λ – 3 – 0, 2λ + 1 – 2, 3λ – 4 – 3 i.e. 5λ – 3, 2λ – 1, 3λ – 7
Since, PM is perpendicular to the line whose direcction ratios are 5, 2, 3,
5(5λ – 3) + 2(2λ – 1) + 3(3λ – 7) = 0
25λ – 15 + 4λ – 2 + 9λ – 21 =0
38λ – 38 = 0 ∴ λ = 1
Substituting λ = 1 in (1), we get.
M = (5 – 3, 2 + 1, 3 – 4) = (2, 3, -1).
Hence, the coordinates of the foot of perpendicular are (2, 3, – 1).
![]()
Question 16.
By computing the shortest distance determine whether following lines intersect each other.
(i) \(\bar{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda(2 \hat{i}-\hat{j}+\hat{k})\) and \(\bar{r}=(2 \hat{i}+2 \hat{j}-3 \hat{k})+\mu(\hat{i}+\hat{j}-2 \hat{k})\)
Solution:
The shortest distance between the lines
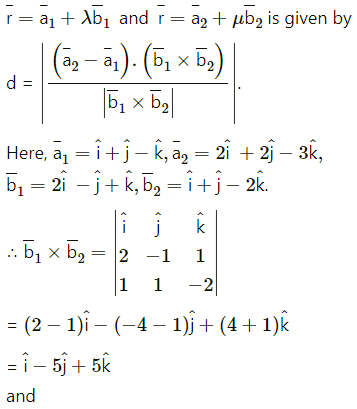
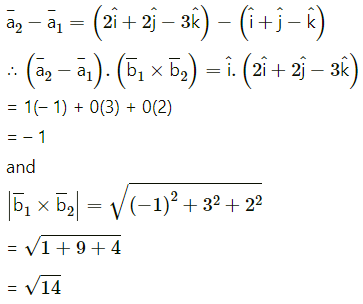
Shortest distance between the lines is 0.
∴ the lines intersect each other.
(ii) \(\frac{x-5}{4}=\frac{y-7}{5}=\frac{z+3}{5}\) and x – 6 = y – 8 = z + 2.
Solution:
The shortest distance between the lines
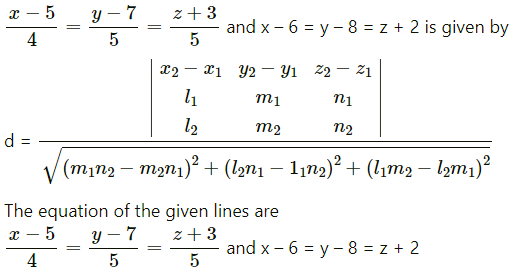
∴ x1 = 5, y1 = 7, z1 = 3, x2 = 6, y2 = 8, z2 = 2,
l1 = 4, m1 = 5, n1 = 1, l2 = 1, m2 = -2, n2 = 1
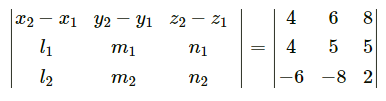
= 4(-6 + 2) – 6(7 – 1) + 8(-14 + 6)
= -16 – 36 – 64
= -116
and
(m1n2 – m2n1)2 + (l2n1 – l1n2)2 + (l1m2 – l2m1)2
= (-6 + 2)2 + (1 – 7)2 + (1 – 7)2 + (-14 + 6)2
= 16 + 36 + 64
= 116
Hence, the required shortest distance between the given lines
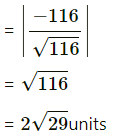
or
Shortest distance between the lines is 0.
∴ the lines intersect each other.
Question 17.
If lines \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}\) and \(\frac{x-2}{1}=\frac{y+m}{2}=\frac{z-2}{1}\) intersect each other then find m.
Solution:

Here, (x1, y1, z1) ≡ (1, -1, 1),
(x2, y2, z2) ≡ (2, -m, 2),
a1 = 2, b1 = 3, c1 = 4,
a2 = 1, b2 = 2, c2 = 1
Substituting these values in (1), we get
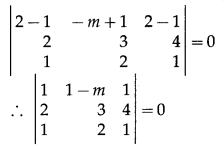
∴ 1(3 – 8) – (1 – m)(2 – 4) + 1 (4 – 3) = 0
∴ -5 + 2 – 2m + 1 = 0
∴ -2m = 2
∴ m = -1.
![]()
Question 18.
Find the vector and Cartesian equations of the line passing through the point (-1, -1, 2) and parallel to the line 2x – 2 = 3y + 1 = 6z – 2.
Solution:
Let \(\bar{a}\) be the position vector of the point A (-1, -1, 2) w.r.t. the origin.
Then \(\bar{a}=-\hat{i}-\hat{j}+2 \hat{k}\)
The equation of given line is
x – 2 = 3y + 1 = 6z – 2.
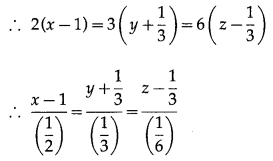
The direction ratios of this line are

Question 19.
Find the direction cosines of the line \(\bar{r}=\left(-2 \hat{i}+\frac{5}{2} \hat{j}-\hat{k}\right)+\lambda(2 \hat{i}+3 \hat{j})\).
Solution:

Question 20.
Find the Cartesian equation of the line passing through the origin which is perpendicular to x – 1 = y – 2 = z – 1 and intersects the \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}\).
Solution:
Let the required line have direction ratios a, b, c
Since the line passes through the origin, its cartesian equations are
\(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}\) …(1)
This line is perpendicular to the line
x – 1 = y – 2 = z – 1 whose direction ratios are 1, 1, 1.

∴ 1(4b – 3c) + 1(4a – 2c) + 1(3a – 2b) = 0
∴ 4b – 3c + 4a – 2c + 3a – 2b = 0
∴ 7a + 2b – 5c = 0
From (2) and (3), we get

![]()
Question 21.
Write the vector equation of the line whose Cartesian equations are y = 2 and 4x – 3z + 5 = 0.
Solution:
4x – 3z + 5 = 0 can be written as

This line passes through the point A(0, 2, \(\frac{5}{3}\)) position vector is \(\bar{a}=2 \hat{j}+\frac{5}{3} \hat{k}\)
Also the line has direction ratio 3, 0, 4.
If \(\bar{b}\) is a vector parallel to the line, then \(\bar{b}=3 \hat{i}+4 \hat{k}\)
The vector equation of the line passing through A(\(\bar{a}\)) and parallel to \(\bar{b}\) is \(\bar{r}=\bar{a}+\lambda \bar{b}\) where λ is \(\bar{a}\) scalar,
∴ the vector equation of the required line is
\(\bar{r}=\left(2 \hat{j}+\frac{5}{3} \hat{k}\right)+\lambda(3 \hat{i}+4 \hat{k})\).
Question 22.
Find the co-ordinates of points on the line \(\frac{x-1}{1}=\frac{y-2}{-2}=\frac{z-3}{2}\) which are at the distance 3 unit from the base point A(1, 2, 3).
Solution:
The cartesian equations of the line are \(\frac{x-1}{1}=\frac{y-2}{-2}=\frac{z-3}{2}\) = λ
The coordinates of any point on this line are given by
x = λ + 1, y = -2λ + 2, z = 2λ + 3
Let M(λ + 1, -2λ + 2, 2λ + 3) … (1)
be the point on the line whose distance from A(1, 2, 3) is 3 units.
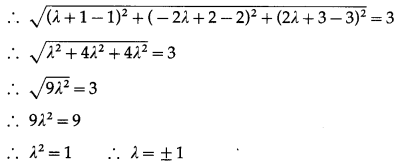
When λ = 1, M = (1 + 1, -2 + 2, 2 + 3) … [By (1)]
i. e. M = (2, 0, 5)
When λ = -1, M = (1 – 1, 2 + 2, -2 + 3) … [By (1)]
i. e. M = (0, 4, 1)
Hence, the coordinates of the required points are (2, 0, 5) and (0, 4, 1).