Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 3 Motion in a Plane Textbook Exercise Questions and Answers.
Maharashtra State Board 11th Physics Solutions Chapter 3 Motion in a Plane
1. Choose the correct option.
Question 1.
An object thrown from a moving bus is on example of __________
(A) Uniform circular motion
(B) Rectilinear motion
(C) Projectile motion
(D) Motion in one dimension
Answer:
(C) Projectile motion
Question 2.
For a particle having a uniform circular motion, which of the following is constant ____________.
(A) Speed
(B) Acceleration
(C) Velocity
(D) Displacement
Answer:
(A) Speed
![]()
Question 3.
The bob of a conical pendulum undergoes ___________
(A) Rectilinear motion in horizontal plane
(B) Uniform motion in a horizontal circle
(C) Uniform motion in a vertical circle
(D) Rectilinear motion in vertical circle
Answer:
(B) Uniform motion in a horizontal circle
Question 4.
For uniform acceleration in rectilinear motion which of the following is not correct?
(A) Velocity-time graph is linear
(B) Acceleration is the slope of velocity time graph
(C) The area under the velocity-time graph equals displacement
(D) Velocity-time graph is nonlinear
Answer:
(D) Velocity-time graph is nonlinear
Question 5.
If three particles A, B and C are having velocities \(\overrightarrow{\mathrm{v}}_{A}\), \(\overrightarrow{\mathrm{v}}_{B}\) and \(\overrightarrow{\mathrm{v}}_{C}\) which of the following formula gives the relative velocity of A with respect to B
(A) \(\overrightarrow{\mathrm{v}}_{A}\) + \(\overrightarrow{\mathrm{v}}_{B}\)
(B) \(\overrightarrow{\mathrm{v}}_{A}\) – \(\overrightarrow{\mathrm{v}}_{C}\) + \(\overrightarrow{\mathrm{v}}_{B}\)
(C) \(\overrightarrow{\mathrm{v}}_{A}\) – \(\overrightarrow{\mathrm{v}}_{B}\)
(D) \(\overrightarrow{\mathrm{v}}_{C}\) – \(\overrightarrow{\mathrm{v}}_{A}\)
Answer:
(C) \(\overrightarrow{\mathrm{v}}_{A}\) – \(\overrightarrow{\mathrm{v}}_{B}\)
2. Answer the following questions.
Question 1.
Separate the following in groups of scalar and vectors: velocity, speed, displacement, work done, force, power, energy, acceleration, electric charge, angular velocity.
Answer:
Scalars
Speed, work done, power, energy, electric charge.
Vectors
Velocity, displacement, force, acceleration, angular velocity (pseudo vector).
![]()
Question 2.
Define average velocity and instantaneous velocity. When are they same?
Answer:
Average velocity:
- Average velocity (\(\overrightarrow{\mathrm{v}}_{\mathrm{av}}\)) of an object is the displacement (\(\Delta \overrightarrow{\mathrm{x}}\)) of the object during the time interval (∆t) over which average velocity is being calculated, divided by that time interval.
- Average velocity = (\(\frac{\text { Displacement }}{\text { Time interval }}\))
\(\overrightarrow{\mathrm{V}_{\mathrm{av}}}=\frac{\overrightarrow{\mathrm{x}}_{2}-\overrightarrow{\mathrm{x}}_{1}}{\mathrm{t}_{2}-\mathrm{t}_{1}}=\frac{\Delta \overrightarrow{\mathrm{x}}}{\Delta \mathrm{t}}\) - Average velocity is a vector quantity.
- Its SI unit is m/s and dimensions are [M0L1T-1]
- For example, if the positions of an object are x +4 m and x = +6 m at times t = O and t = 1 minute respectively, the magnitude of its average velocity during that time is Vav = (6 – 4)1(1 – 0) = 2 m per minute and its direction will be along the positive X-axis.
∴ \(\overrightarrow{\mathrm{v}}_{\mathrm{av}}\) = 2 i m/min
Where, i = unit vector along X-axis.
Instantaneous velocity:
- The instantaneous velocity (\(\overrightarrow{\mathrm{V}}\)) is the limiting value of ¡he average velocity of the object over a small time interval (∆t) around t when the value of lime interval goes to zero.
- It is the velocity of an object at a given instant of time.
- \(\overrightarrow{\mathrm{v}}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{\mathrm{x}}}{\Delta \mathrm{t}}=\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\)
where \(\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\) derivative of \(\overrightarrow{\mathrm{x}}\) with respect to t.
In case of uniform rectilinear motion, i.e., when an object is moving with constant velocity along a straight line, the average and instantaneous velocity remain same.
Question 3.
Define free fall.
Answer:
The motion of any object under the influence of gravity alone is called as free fall.
Question 4.
If the motion of an object is described by x = f(t) write formulae for instantaneous velocity and acceleration.
Answer:
- Instantaneous velocity of an object is given as,
\(\overrightarrow{\mathrm{v}}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{\mathrm{x}}}{\Delta \mathrm{t}}=\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\) - Motion of the object is given as, x = f(t)
- The derivative f ‘(f) represents the rate of change of the position f (t) at time t, which is the instantaneous velocity of the object.
∴ \(\vec{v}=\frac{\mathrm{d} \overrightarrow{\mathrm{x}}}{\mathrm{dt}}\) = f'(t) - Acceleration is defined as the rate of change of velocity with respect to time.
- The second derivative of the position function f “(t) represents the rate of change of velocity i.e., acceleration.
∴ \(\overrightarrow{\mathrm{a}}=\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}=\frac{\mathrm{d}^{2} \mathrm{x}}{\mathrm{dt}^{2}}\) = f”(t)
Question 5.
Derive equations of motion for a particle moving in a plane and show that the motion can be resolved in two independent motions in mutually perpendicular directions.
Answer:
- Consider an object moving in an x-y plane. Let the initial velocity of the object be \(\overrightarrow{\mathrm{u}}\) at t = 0 and its velocity at time t be \(\overrightarrow{\mathrm{v}}\).
- As the acceleration is constant, the average acceleration and the instantaneous acceleration will be equal.
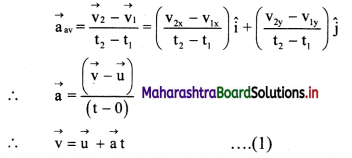
This is the first equation of motion in vector form. - Let the displacement of the object from time t
= 0 to t be \(\overrightarrow{\mathrm{s}}\)
For constant acceleration, \(\overrightarrow{\mathrm{v}}_{\mathrm{av}}=\frac{\overrightarrow{\mathrm{v}}+\overrightarrow{\mathrm{u}}}{2}\)
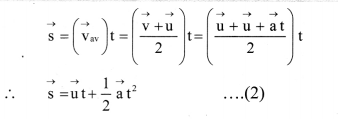
This is the second equation of motion in vector form. - Equations (1) and (2) can be resolved into their x and y components so as to get corresponding scalar equations as follows.
vx = ux + axt ………….. (3)
vy = uy + ay t …………… (4)
sx = uxt + \(\frac{1}{2}\) axt2 ………….. (5)
sy = uyt + \(\frac{1}{2}\) ayt2 ………..(6) - It can be seen that equations (3) and (5) involve only the x components of displacement, velocity and acceleration while equations (4) and (6) involve only the y components of these quantities.
- Thus, the motion along the x direction of the object is completely controlled by the x components of velocity and acceleration while that along the y direction is completely controlled by the y components of these quantities.
- This shows that the two sets of equations are independent of each other and can be solved independently.
![]()
Question 6.
Derive equations of motion graphically for a particle having uniform acceleration, moving along a straight line.
Answer:
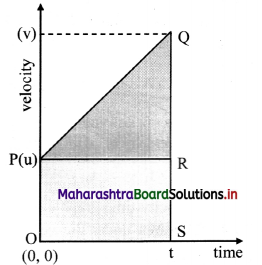
- Consider an object starting from position x = 0 at time t = 0. Let the velocity at time (t = 0) and t be u and v respectively.
- The slope of line PQ gives the acceleration. Thus
∴ a = \(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}-0}=\frac{\mathrm{v}-\mathbf{u}}{\mathrm{t}}\)
∴ v = u + at …………… (1)
This is the first equation of motion. - The area under the curve in velocity-time graph gives the displacement of the object.
∴ s = area of the quadrilateral OPQS = area of rectangle OPRS + area of triangle PQR.
= ut + \(\frac{1}{2}\) (v – u) t
But, from equation (1)
at = v – u
∴ s = ut + \(\frac{1}{2}\) at2
This is the second equation of motion, - The velocity is increasing linearly with time as acceleration is constant. The displacement is given as,
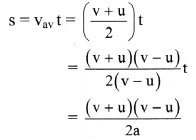
∴ s = (v2 – u2) / (2a)
∴ v2 – u2 = 2as
This is the third equation of motion.
Question 7.
Derive the formula for the range and maximum height achieved by a projectile thrown from the origin with initial velocity \(\vec{u}\) at an angel θ to the horizontal.
Answer:
Expression for range:
- Consider a body projected with velocity \(\vec{u}\), at an angle θ of projection from point O in the co-ordinate system of the XY- plane, as shown in figure.
- The initial velocity \(\vec{u}\) can be resolved into two rectangular components:
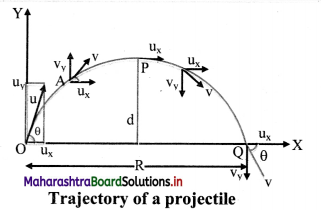
ux = u cos θ (Horizontal component)
uy = u sin θ (Vertical component) - The horizontal component remains constant throughout the motion due to the absence of any force acting in that direction, while the vertical component changes according to
vy = uy + ayt
with ay = -g and uy = u sinθ - Thus, the components of velocity of the projectile at time t are given by,
vx = ux = u cos θ
vy = ux – gt = usin θ – gt - Similarly, the components of displacements of the projectile in the horizontal and vertical directions at time t are given by,
s = (u cosθ) t
sy = (usinθ)t – \(\frac{1}{2}\) gt2 - At the highest point, the time of ascent of the projectile is given as,
tA = \(\frac{u \sin \theta}{g}\) …………..(2) - The total time in air i.e., time of flight is given as, T = 2tA = \(\frac{2u \sin \theta}{g}\) …… (3)
- The total horizontal distance travelled by the particle in this time T is given as,
R = ux ∙ T
R = u cos θ ∙ (2tA)
R = u cos θ ∙ \(\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}\) ……………[From (3)]
R = \(\frac{u^{2}(2 \sin \theta \cdot \cos \theta)}{g}\)
R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\) ………..[∵ sin 2θ = 2sin∙cosθ]
This is required expression for horizontal range of the projectile.
Expression for maximum height of a projectile:
The maximum height H reached by the projectile is the distance travelled along the vertical (y) direction in time tA.
Substituting sy = H and t = ta in equation (1),
we have,
H = (u sin θ)tA – \(\frac{1}{2}\) gtA2
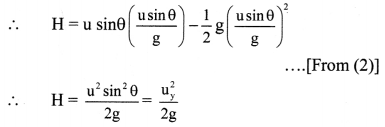
This equation represents maximum height of projectile.
Question 8.
Show that the path of a projectile is a parabola.
Answer:
- Consider a body projected with velocity initial velocity \(\vec{u}\) , at an angle θ of projection from point O in the co-ordinate system of the XY-plane. as shown in figure.
- The initial velocity \(\vec{u}\) can be resolved into two rectangular components:
ux = u cos θ (Horizontal component)
uy = u sin θ (Vertical component) - The horizontal component remains constant throughout the motion due to the absence of any force acting in that direction, while the vertical component changes according to,
vy = uy + ay t
with ay, = -g and uy = u sinθ - Thus, the components of velocity of the projectile at time t are given by,
vx = ux = u cosθ
vy = uy – gt = u sinθ – gt - Similarly, the components of displacements of the projectile in the horizontal and vertical directions at time t are given by,
sx = (u cosθ)t …………..(1)
sy = (u sinθ)t – \(\frac{1}{2}\) gt2 ………………. (2) - As the projectile starts from x = O, we can use
sx = x and sy = y.
Substituting sx = x in equation (1),
x = (u cosθ) t
∴ t = \(\frac{\mathrm{X}}{(\mathrm{u} \cos \theta)}\) …………….. (3)
Substituting, sy in equation (2),
y = (u sinθ)t – \(\frac{1}{2}\) gt2 …………… (4)
Substituting equation (3) in equation (4), we have,
y = u sin θ (\(\frac{\mathrm{X}}{(\mathrm{u} \cos \theta)}\)) – \(\frac{1}{2}\) (\(\frac{\mathrm{X}}{(\mathrm{u} \cos \theta)}\))2 g
∴ y = x (tan θ) – (\(\frac{g}{2 u^{2} \cos ^{2} \theta}\))x2 ………………. (5)
Equation (5) represents the path of the projectile. - If we put tan θ = A and g/2u2cos2θ = B then equation (5) can be written as y = Ax – Bx2 where A and B are constants. This is equation of parabola. Hence, path of projectile is a parabola.
![]()
Question 9.
What is a conical pendulum? Show that its time period is given by 2π \(\sqrt{\frac{l \cos \theta}{g}}\), where l is the length of the string, θ is the angle that the string makes with the vertical and g is the acceleration due to gravity.
Answer:
A simple pendulum, Ch i given such a motion that the bob describes a horizontal circle and the string making a constant angle with the vertical describes a cone, is called a conical pendulum.
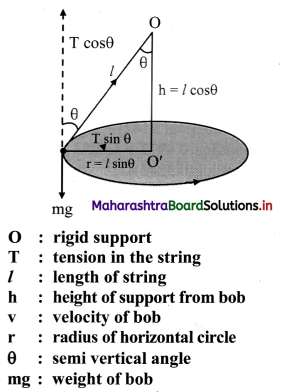
- Consider a bob of mass m tied to one end of a string of length ‘P and other end is fixed to rigid support.
- Let the bob be displaced from its mean position and whirled around a horizontal circle of radius ‘r’ with constant angular velocity ω, then the bob performs U.C.M.
- During the motion, string is inclined to the vertical at an angle θ as shown in the figure above.
- In the displaced position, there are two forces acting on the bob.
- The weight mg acting vertically downwards.
- The tension T acting upward along the string.
- The tension (T) acting in the string can be resolved into two components:
- T cosθ acting vertically upwards.
- T sinθ acting horizontally towards centre of the circle.
- Since, there is no net force, vertical component T cosθ balances the weight and horizontal component T sinθ provides the necessary centripetal force.
∴ T cos θ = mg ……………. (1)
T sin θ = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) = mrω2 ……….. (2) - Dividing equation (2) by (1),
tan θ = \(\frac{\mathrm{v}^{2}}{\mathrm{rg}}\) ……….. (3)
Therefore, the angle made by the string with the vertical is θ = tan-1 (\(\frac{\mathrm{v}^{2}}{\mathrm{rg}}\)) - Since we know v = \(\frac{2 \pi \mathrm{r}}{\mathrm{T}}\)
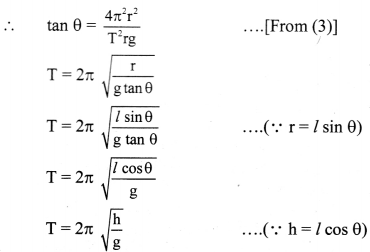
where l is length of the pendulum and h is the vertical distance of the horizontal circle from the fixed point O.
![]()
Question 10.
Define angular velocity. Show that the centripetal force on a particle undergoing uniform circular motion is -mω2\(\vec{r}\).
Answer:
Angular velocity of a particle is the rate of change of angular displacement.
Expression for centripetal force on a particle undergoing uniform circular motion:
i) Suppose a particle is performing U.C.M in anticlockwise direction.
The co-ordinate axes are chosen as shown in the figure.
Let,
A = initial position of the particle which lies on positive X-axis
P = instantaneous position after time t
θ = angle made by radius vector
ω = constant angular speed
\(\overrightarrow{\mathrm{r}}\) = instantaneous position vector at time t
ii) From the figure,
\(\overrightarrow{\mathrm{r}}=\hat{\mathrm{i}} \mathrm{x}+\hat{\mathrm{j}} \mathrm{y}\)
where, \(\hat{\mathrm{i}}\) and \(\hat{\mathrm{j}}\) are unit vectors along X-axis and Y-axis respectively.
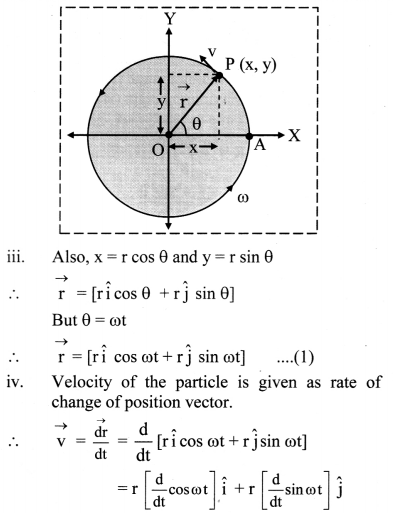

Negative sign shows that direction of acceleration is opposite to the direction of position vector. Equation (3) is the centripetal acceleration.
vii) Magnitude of centripetal acceleration is given by a = ω2r
viii) The force providing this acceleration should also be along the same direction, hence centripetal.
∴ \(\overrightarrow{\mathrm{F}}\) = m\(\overrightarrow{\mathrm{a}}\) = -mω2\(\overrightarrow{\mathrm{r}}\)
This is the expression for the centripetal force on a particle undergoing uniform circular motion.
ix) Magnitude of F = mω2r = \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}\) = mωv
[Note: The definition of angular velocity is not mentioned in this chapter but is in Ch.2 Mathematical Methods.]
3. Solve the following problems.
Question 1.
An aeroplane has a run of 500 m to take off from the runway. It starts from rest and moves with constant acceleration to cover the runway in 30 sec. What is the velocity of the aeroplane at the take off ?
Answer:
Given: Length of runway (s) = 500 m, t = 30 s
To find: Velocity (y)
Formulae. i) s = ut + \(\frac{1}{2}\) at2
ii) v = u + at
Calculation: As the plane was initially at rest, u = 0
From formula (1),
500 = 0 + \(\frac{1}{2}\) × a × (30)2
∴ 500 = 450 a
∴ a = \(\frac{10}{9}\) m/s2
From formula (ii),
v = 0 + \(\frac{10}{9}\) × 30
∴ v = \(\frac{100}{3}\) m/s = (\(\frac{100}{3} \times \frac{18}{5}\)) km/hr
∴ v = 120 km/hr
The velocity of the aeroplane at the take off is 120 km/hr.
![]()
Question 2.
A car moving along a straight road with a speed of 120 km/hr, is brought to rest by applying brakes. The car covers a distance of 100 m before it stops. Calculate
(i) the average retardation of the car
(ii) time taken by the car to come to rest.
Answer:
Given: u = 120 kmh-1 = 120 × \(\frac{5}{18}\) = \(\frac{100}{3}\) ms-1
s = 100 m, v = 0
To find: i) Average retardation of the car (a)
ii) Time taken by car (t)
Formulae: i) v2 – u2 = 2as
ii) v = u + at
Calculation: From formula (i),

i) Average retardation of the car is \(\frac{50}{9}\) ms2 (in magnitude).
ii) Time taken by the car to come to rest is 6 s.
Question 3.
A car travels at a speed of 50 km/hr for 30 minutes, at 30 km/hr for next 15 minutes and then 70 km/hr for next 45 minutes. What is the average speed of the car?
Answer:
Given: v1 = 50 km/hr. t1 = 30 minutes = 0.5 hr,
v2 = 30 km/hr, t2 = 15 minutes = 0.25 hr,
v3 = 70 km/hr, t3 = 45 minutes 0.75 hr
To find: Average speed of car (vav)
Formula vav = \(\frac{\text { total path length }}{\text { total time interval }}\)
Calculation:
Path length,
x1 = v1 × t1 = 50 × 0.5 = 25km
x2 = v2 × t2 = 30 × 0.25 = 7.5 km
x3 = v3 × t3 = 70 × 0.75 = 52.5 km
From formula,
vav = \(\frac{x_{1}+x_{2}+x_{3}}{t_{1}+t_{2}+t_{3}}\)
∴ vav = \(\frac{25+7.5+52.5}{0.5+0.25+0.75}=\frac{85}{1.5}\)
∴ vav = 56.66 km/hr
Question 4.
A velocity-time graph is shown in the adjoining figure.
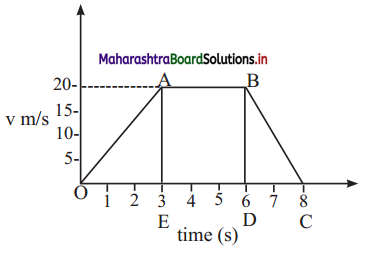
Determine:
- initial speed of the car
- maximum speed attained by the car
- part of the graph showing zero acceleration
- part of the graph showing constant retardation
- distance travelled by the car in first 6 sec.
Answer:
- Initial speed is at origin i.e. 0 m/s.
- Maximum speed attained by car, vmax = speed from A to B = 20 m/s.
- The part of the graph which shows zero acceleration is between t = 3 s and t = 6 s i.e., AB. This is because, during AB there is no change in velocity.
- The graph shows constant retardation from t = 6 s to t = 8 s i.e., BC.
- Distance travelled by car in first 6 s
= Area of OABDO
= A(△OAE) + A(rect. ABDE)
= \(\frac{1}{2}\) × 3 × 20 + 3 × 20
= 30 + 60
∴ Distance travelled by car in first 6 s = 90 m
Question 5.
A man throws a ball to maximum horizontal distance of 80 meters. Calculate the maximum height reached.
Answer:
Given: R = 80m
To find: Maximum height reached (Hmax)
Formula: Rmax = 4Hmax
Calculation: From formula,
∴ Hmax = \(\frac{\mathrm{R}_{\max }}{4}=\frac{80}{4}\) = 20 m
The maximum height reached by the ball is 20m.
![]()
Question 6.
A particle is projected with speed v0 at angle θ to the horizontal on an inclined surface making an angle Φ (Φ < θ) to the horizontal. Find the range of the projectile along the inclined surface.
Answer:
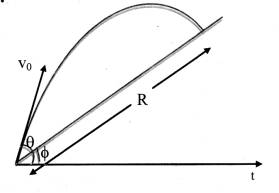
i) The equation of trajectory of projectile is given by,
y(tan θ)x – (\(\frac{\mathrm{g}}{2 \mathrm{u}^{2} \cos ^{2} \theta}\))x2 …………..(1)
ii) In this case to find R substitute,
y = R sinΦ ………….. (2)
x = R cosΦ ………….. (3)
iii) From equations (1), (2) and (3),
we have,
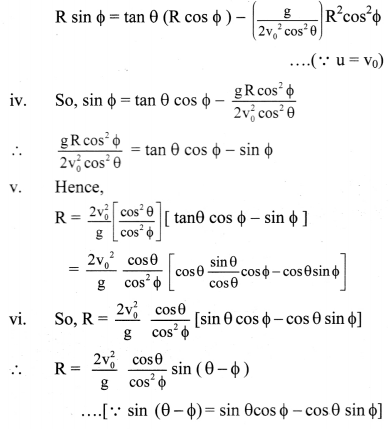
Question 7.
A metro train runs from station A to B to C. It takes 4 minutes in travelling from station A to station B. The train halts at station B for 20 s. Then it starts from station B and reaches station C in the next 3 minutes. At the start, the train accelerates for 10 sec to reach the constant speed of 72 km/hr. The train moving at the constant speed is brought to rest in 10 sec. at next station.
(i) Plot the velocity-time graph for the train travelling from station A to B to C.
(ii) Calculate the distance between stations A, B, and C.
Answer:
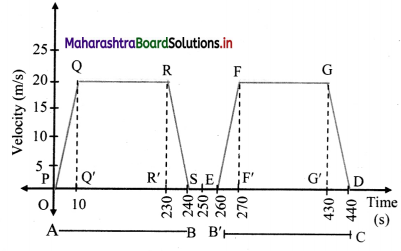
The metro train travels from station A to station B in 4 minutes = 240 s.
The trains halts at station B for 20 s.
The train travels from station B’ to station C in 3 minutes= 180 s.
∴ Total time taken by the metro train in travelling from station A to B to C
= 240 + 20 + 180 = 440 s.
At start, the train accelerates for 10 seconds to reach a constant speed of 72 km/hr = 20 m/s.
The train moving is brought to rest in 10 s at next station.
The velocity-time graph for the train travelling from station A to B to C is as follows:
Distance travelled by the train from station A to station B
= Area of PQRS
= A ( △PQQ’) A (☐QRR’) + A(SRR’)
= (\(\frac{1}{2}\) × 10 × 20 + (220 × 20) + (\(\frac{1}{2}\) 10 × 20)
= 100 + 4400 + 100
= 4600m = 4.6km
Distance travelled by the train from station B’ to station C
= Area of EFGD
= A(△EFF’) + A(☐F’FGG’) + A(△DGG’)
= (\(\frac{1}{2}\) × 10 × 20) × (160 × 20) + (\(\frac{1}{2}\) × 10 × 20)
= 100 + 3200 + 100
= 3400m = 3.4km
Question 8.
A train is moving eastward at 10 m/sec. A waiter is walking eastward at 1.2m/sec; and a fly is flying toward the north across the waiter’s tray at 2 m/s. What is the velocity of the fly relative to Earth.
Answer:
Given

Question 9.
A car moves in a circle at the constant speed of 50 m/s and completes one revolution in 40 s. Determine the magnitude of the acceleration of the car.
Answer:
Given: v = 50 m/s, t = 40 s, s = 2πr
To find: acceleration (a)
Formulae: i) v = \(\frac{\mathrm{s}}{\mathrm{t}}\)
ii) a = \(\frac{\mathrm{v}^{2}}{\mathrm{r}}\)
Calculation: From formula (i),
50 = \(\frac{2 \pi \mathrm{r}}{40}\)
∴ r = \(\frac{50 \times 40}{2 \pi}\)
∴ r = \(\frac{1000}{\pi}\) cm
From formula (ii),
a = \(\frac{v^{2}}{r}=\frac{50^{2}}{1000 / \pi}\)
∴ a = \(\frac{5 \pi}{2}\) = 7.85 m/s2
The magnitude of acceleration of the car is 7.85 m/s.
Alternate method:
Given: v = 50 m/s, t = 40 s,
To find: acceleration (a)
Formula: a = rω2 = vω
Calculation: From formula,
a = vω
= v(\(\frac{2 \pi}{\mathrm{t}}\))
= 50(\(\frac{2 \times 3.142}{40}\))
= \(\frac{5}{2}\) × 3.142
∴ a = 7.85m/s2
![]()
Question 10.
A particle moves in a circle with constant speed of 15 m/s. The radius of the circle is 2 m. Determine the centripetal acceleration of the particle.
Answer:
Given: v = 15 m/s, r = 2m
To find: Centripetal acceleration (a)
Formula: a = \(\frac{\mathrm{v}^{2}}{\mathrm{r}}\)
Calculation: From formula,
a = \(\frac{(15)^{2}}{2}=\frac{225}{2}\)
∴ a = 112.5m/s2
The centripetal acceleration of the particle is 112.5 m/s2.
Question 11.
A projectile is thrown at an angle of 30° to the horizontal. What should be the range of initial velocity (u) so that its range will be between 40m and 50 m? Assume g = 10 m s-2.
Answer:
Given: 40 ≤ R ≤ 50, θ = 300, g = 10 m/s2
To find: Range of initial velocity (u)
Formula: R = \(\frac{\mathrm{u}^{2} \sin (2 \theta)}{\mathrm{g}}\)
Calculation: From formula,
The range of initial velocity,

∴ 21.49m/s ≤ u ≤ 24.03m/s
The range of initial velocity should be between 21.49 m/s ≤ u ≤ 24.03 m/s.
11th Physics Digest Chapter 3 Motion in a Plane Intext Questions and Answers
Can you recall? (Textbook Page No. 30)
Question 1.
What ¡s meant by motion?
Answer:
The change ¡n the position of an object with respect to its surroundings is called motion.
Question 2.
What Is rectilinear motion?
Answer:
Motion in which an object travels along a straight line is called rectilinear motion.
Question 3.
What is the difference between displacement and distance travelled?
Answer:
- Displacement is the shortest distance between the initial and final points of movement.
- Distance is the actual path followed by a body between the points in which it moves.
Question 4.
What is the difference between uniform and non-uniform motion?
Answer:
- A body is said to have uniform motion if it covers equal distances in equal intervals of time.
- A body is said to have non-uniform motion if it covers unequal distances in equal intervals of time.
Internet my friend (Textbook Page No. 44)
i. hyperphysics.phy-astr.gsu.eduJhbase/mot.html#motcon
ii. www .college-physics.comlbook/mechanics
[Students are expected to visit the above mentioned webs ires and collect more information.]