Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 4 Laws of Motion Textbook Exercise Questions and Answers.
Maharashtra State Board 11th Physics Solutions Chapter 4 Laws of Motion
1. Choose the correct answer.
Question 1.
Consider the following pair of forces of equal magnitude and opposite directions:
(P) Gravitational forces are exerted on each other by two-point masses separated by a distance.
(Q) Couple of forces are used to rotate a water tap.
(R) Gravitational force and normal force are experienced by an object kept on a table.
For which of these pair/pairs the two forces do NOT cancel each other’s translational
effect?
(A) Only P
(B) Only P and Q
(C) Only R
(D) Only Q and R
Answer:
(A) Only P
Question 2.
Consider the following forces: (w) Force due to tension along a string, (x) Normal force given by a surface, (y) Force due to air resistance, and (z) Buoyant force or upthrust given by a fluid.
Which of these are electromagnetic forces?
(A) Only w, y, and z
(B) Only w, x, and y
(C) Only x, y and z
(D) All four.
Answer:
(D) All four.
![]()
Question 3.
At a given instant three-point masses m, 2m, and 3m are equidistant from each other. Consider only the gravitational forces between them. Select correct statement/s for this instance only:
(A) Mass m experiences maximum force.
(B) Mass 2m experiences a maximum force.
(C) Mass 3m experiences a maximum force.
(D) All masses experience a force of the same magnitude.
Answer:
(C) Mass 3m experiences a maximum force.
Question 4.
The rough surface of a horizontal table offers a definite maximum opposing force to initiate the motion of a block along with the table, which is proportional to the resultant normal force given by the table. Forces F1 and F2 act at the same angle θ with the horizontal and both are just initiating the sliding motion of the block along with the table. Force F1 is a pulling force while the force F2 is a pushing force. F2 > F1, because
(A) Component of F2 adds up to weight to increase the normal reaction.
(B) Component of F1 adds up to weight to increase the normal reaction.
(C) Component of F2 adds up to the opposing force.
(D) Component of F1 adds up to the opposing force.
Answer:
(A) Component of F2 adds up to weight to increase the normal reaction.
Question 5.
A mass 2m moving with some speed is directly approaching another mass m moving with double speed. After some time, they collide with coefficient of restitution 0.5. Ratio of their respective speeds after collision is
(A) 2/3
(B) 3/2
(C) 2
(D) ½
Answer:
(B) 3/2
Question 6.
A uniform rod of mass 2m is held horizontal by two sturdy, practically inextensible vertical strings tied at its ends. A boy of mass 3m hangs himself at one third length of the rod. Ratio of the tension in the string close to the boy to that in the other string is
(A) 2
(B) 1.5
(C) 4/3
(D) 5/3
Answer:
(B) 1.5
Question 7.
Select WRONG statement about centre of mass:
(A) Centre of mass of a ‘C’ shaped uniform rod can never be a point on that rod.
(B) If the line of action of a force passes through the centre of mass, the moment of that force is zero.
(C) Centre of mass of our Earth is not at its geometrical centre.
(D) While balancing an object on a pivot, the line of action of the gravitational force of the earth passes through the centre of mass of the object.
Answer:
(D) While balancing an object on a pivot, the line of action of the gravitational force of the earth passes through the centre of mass of the object.
Question 8.
For which of the following objects will the centre of mass NOT be at their geometrical centre?
(I) An egg
(II) a cylindrical box full of rice
(III) a cubical box containing assorted sweets
(A) Only (I)
(B) Only (I) and (II)
(C) Only (III)
(D) All, (I), (II) and (III).
Answer:
(D) All, (I), (II) and (III).
2. Answer the following questions.
Question 1.
In the following table, every entry on the left column can match with any number of entries on the right side. Pick up all those and write respectively against A, B, C and D.
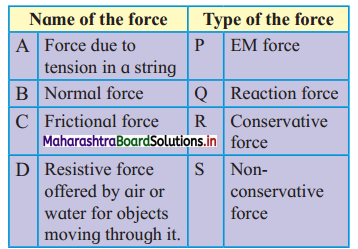
Answer:
- Force due to tension in string: Electromagnetic (EM) force, reaction force, non-conservative force.
- Normal force: Electromagnetic (EM) force, non-conservative force. Reaction force
- Frictional force: Electromagnetic (EM) force, reaction force, non-conservative force.
- Resistive force offered by air or water for objects moving through it: Electromagnetic (EM) force, non-conservative force.
![]()
Question 2.
In real life objects, never travel with uniform velocity, even on a horizontal surface, unless something is done? Why
is it so? What is to be done?
Answer:
- According to Newton’s first law, for a body to achieve uniform velocity, the net force acting on it should be zero.
- In real life, a body in motion is constantly being acted upon by resistive or opposing force like friction, in the direction opposite to that of the motion.
- To overcome these opposing forces, an additional external force is required. Thus, the net force is not maintained at zero, making it hard to achieve uniform velocity.
Question 3.
For the study of any kind of motion, we never use Newton’s first law of motion directly. Why should it be studied?
Answer:
- Newton’s first law shows an equivalence between the ‘state of rest’ and ‘state of uniform motion along a straight line.’
- Newton’s first law of motion defines force as a physical quantity that brings about a change in ‘state of rest’ or ‘state of .uniform motion along a straight line’ of a body.
- Newton’s first law of motion defines inertia as a fundamental property of every physical object by which the object resists any change in its state of rest or of uniform motion along a straight line. Due to all these reasons, Newton’s first law should be studied.
Question 4.
Are there any situations in which we cannot apply Newton’s laws of motion? Is there any alternative for it?
Answer:
- Limitation: Newton’s laws of motion cannot be applied for objects moving in non-inertial (accelerated) frame of reference.
Alternative solution: For non-inertial (accelerated) frame of reference, pseudo force needs to be considered along with all the other forces. - Limitation: Newton’s laws of motion are applicable to point objects and rigid bodies. Alternative solution: Body needs to be approximated as a particle as the laws can be applied to individual particles in a rigid body and then summed up over the body.
- Limitation: Newton’s laws of motion cannot be applied for objects moving with speeds comparable to that of light.
Alternative solution: Einstein’s special theory of relativity has to be used. - Limitation: Newton’s laws of motion cannot be applied for studying the behaviour and interactions of objects having atomic or molecular sizes.
Alternative solution: Quantum mechanics has to be used.
Question 5.
You are inside a closed capsule from where you are not able to see anything about the outside world. Suddenly you feel that you are pushed towards your right. Can you explain the possible cause (s)? Is it a feeling or a reality? Give at least one more situation like this.
Answer:
- In a capsule, if we suddenly feel a push towards the right it is because the capsule is in motion and taking a turn towards the left.
- The push towards the right is a feeling. In reality, when the capsule is beginning its turning motion towards the left, we continue in a straight line.
- This happens because we try to maintain our direction of motion while the capsule takes a turn towards the left.
- An external force is required to change our direction of motion. In accordance with one of the inferences from Newton’s first law of motion, in the absence of any external force, we continue to move in a straight line at constant speed and feel the sudden push in the direction opposite to the motion of the capsule.
- Example: While travelling by bus, when the bus takes a sudden turn we feel the push in the opposite direction.
Question 6.
Among the four fundamental forces, only one force governs your daily life almost entirely. Justify the statement by stating that force.
Answer:
- Electromagnetic force is the attractive and repulsive force between electrically charged particles.
- Since electromagnetic force is much stronger than the gravitational force, it dominates all the phenomena on atomic and molecular scales.
- Majority of the forces experienced in our daily life like friction, normal reaction, tension in strings, elastic forces, viscosity etc. are electromagnetic in nature.
- The structure of atoms and molecules, the dynamics of chemical reactions etc. are governed by electromagnetic forces.
Thus, out of the four fundamental forces, electromagnetic force governs our daily life almost entirely.
Question 7.
Find the odd man out:
(i) Force responsible for a string to become taut on stretching
(ii) Weight of an object
(iii) The force due to which we can hold an object in hand.
Answer:
Weight of an object.
Reason: Weight of an object (force due to gravity) is a non-contact force while force responsible for a string to become taut (tension force) and force due to which we can hold an object in hand (normal force) are contact forces.
![]()
Question 8.
You are sitting next to your friend on ground. Is there any gravitational force of attraction between you two? If so, why are you not coming together naturally? Is any force other than the gravitational force of the earth coming in picture?
Answer:
- Yes, there exists a gravitational force between me and my friend sitting beside each other.
- The gravitational force between any two objects is given by, \(\overrightarrow{\mathrm{F}}=\mathrm{G} \frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\) Where,
G = universal gravitational constant, m1 and m2 = mass of the two objects, r = distance between centres of the two objects - Thus, me and my friend attract each other. But due to our small masses, we exert a force on each other, which is too small as compared to the gravitational force of the earth. Hence, me and my friend don’t move towards each other.
- Apart from gravitational force of the earth, there is the normal force and frictional force acting on both me and my friend.
In Chapter 5, you will study about force of gravitation in detail.
Question 9.
Distinguish between:
(A) Real and pseudo forces,
(B) Conservative and non-conservative forces,
(C) Contact and non-contact forces,
(D) Inertial and non-inertial frames of reference.
Answer:
(A) Real and pseudo forces,
| No | Real force | Pseudo Force |
| i. | A force which is produced due to interaction between the objects is called real force. | A pseudo force is one which arises due to the acceleration of the observer’s frame of reference. |
| ii. | Real forces obey Newton’s laws of motion. | Pseudo forces do not obey Newton’s laws of motion. |
| iii. | Real forces are one of the four fundamental forces. | Pseudo forces are not among any of the four fundamental forces. |
| Example: The earth revolves around the sun in circular path due to gravitational force of attraction between the sun and the earth. | Example: Bus is moving with an acceleration (a) on a straight road in forward direction, a person of mass ‘m’ experiences a backward pseudo force of magnitude ‘ma’. |
(B) Conservative and non-conservative forces,
| No | Conservative | Non-conservative forces |
| i. | If work done by or against a force is independent’ of the actual path, the force is said to be a conservative force. | If work done by or against a force is dependent of the actual path, the force is said to be a non- conservative force. |
| ii. | During work done by a conservative force, the mechanical energy is conserved. | During work done by a non conservative force, the mechanical energy may not be conserved. |
| iii. | Work done is completely recoverable. | Work done is not recoverable. |
| Example: gravitational force, magnetic force etc. |
Example: Frictional force, air drag etc. |
(C) Contact and non-contact forces,
| No | Contact forces | Non-contact forces |
| i. | The forces experienced by a body due to physical contact are called contact forces. | The forces experienced by a body without any physical contact are called non-contact forces. |
| ii. | Example: gravitational force, electrostatic force, magnetostatic force etc. | Example: Frictional force, force exerted due to collision, normal reaction etc. |
(D) Inertial and non-inertial frames of reference.
| No. | Inertial frame of reference | Non-inertial frame of reference |
| i | The body moves with a constant velocity (can be zero). | The body moves with variable velocity. |
| ii. | Newton’s laws are | Newton’s laws are |
| iii. | The body does not accelerate. | The body undergoes acceleration. |
| iv. | In this frame, force acting on a body is a real force. | The acceleration of the frame gives rise to a pseudo force. |
| Example: A rocket in inter-galactic space (gravity free space between galaxies) with all its engine shut. | Example: If a car just starts its motion from rest, then during the time of acceleration the car will be in a non- inertial frame of reference. |
Question 10.
State the formula for calculating work done by a force. Are there any conditions or limitations in using it directly? If so, state those clearly. Is there any mathematical way out for it? Explain.
Answer:
- Suppose a constant force \(\overrightarrow{\mathrm{F}}\) acting on a body produces a displacement \(\overrightarrow{\mathrm{S}}\) in the body along the positive X-direction. Then the work done by the force is given as,
W = F.s cos θ
Where θ is the angle between the applied force and displacement. - If displacement is in the direction of the force applied, θ = 0°
W = \(\overrightarrow{\mathrm{F}}\).\(\overrightarrow{\mathrm{s}}\)
Conditions/limitations for application of work formula:
- The formula for work done is applicable only if both force \(\overrightarrow{\mathrm{F}}\) and displacement \(\overrightarrow{\mathrm{s}}\) are constant and finite i.e., it cannot be applied when the force is variable.
- The formula is not applicable in several real- life situations like lifting an object through several thousand kilometres since the gravitational force is not constant. It is not applicable to viscous forces like fluid resistance as they depend upon speed and thus are often not constant with time.
- The method of integration has to be applied to find the work done by a variable force.
Integral method to find work done by a variable force:
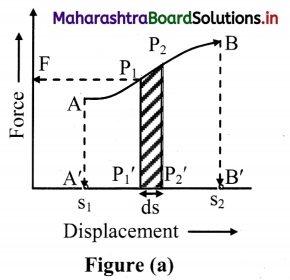
- Let the force vary non-linearly in magnitude between the points A and B as shown in figure (a).
- In order to calculate the total work done during the displacement from s1 to s2, we need to use integration. For integration, we need to divide the displacement into large numbers of infinitesimal (infinitely small) displacements.
- Let at P1, the magnitude of force be F = P1P1‘. Due to this force, the body displaces through infinitesimally small displacement ds, in the direction of force.
It moves from P1 to P2.
∴ \(\mathrm{d} \overrightarrow{\mathrm{s}}=\overrightarrow{\mathrm{P}_{1} \mathrm{P}_{2}}\) - But direction of force and displacement are same, we have
\(\mathrm{d} \overrightarrow{\mathrm{s}}=\mathrm{P}_{1}{ }^{\prime} \mathrm{P}_{2}^{\prime}\) - \(\mathrm{d} \overrightarrow{\mathrm{s}}\) is so small that the force F is practically constant for the displacement. As the force is constant, the area of the strip \(\overrightarrow{\mathrm{F}} \cdot \mathrm{d} \overrightarrow{\mathrm{s}}\) is the work done dW for this displacement.
- Hence, small work done between P1 to P2 is dW and is given by
dW = \(\overrightarrow{\mathrm{F}} \cdot \mathrm{d} \overrightarrow{\mathrm{s}}\) = \(\mathrm{P}_{1} \mathrm{P}_{1}^{\prime} \times \mathrm{P}_{1}^{\prime} \mathrm{P}_{2}^{\prime}\)
= Area of the strip P1P2P2‘P1‘. - The total work done can be found out by dividing the portion AB into small strips like P1P2P2‘P1‘ and taking sum of all the areas of the strips.
∴ W = \int_{s_{1}}^{s 2} \vec{F} \cdot d \vec{s}=\text { Area } A B B^{\prime} A^{\prime}\(\) - Method of integration is applicable if the exact way of variation in \(\overrightarrow{\mathrm{F}}\) and \(\overrightarrow{\mathrm{s}}\) is known and that function is integrable.
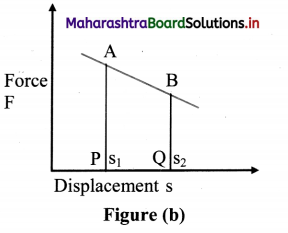
- The work done by the non-linear variable force is represented by the area under the portion of force-displacement graph.
- Similarly, in case of a linear variable force, the area under the curve from s1 to s2 (trapezium APQB) gives total work done W [figure (b)].
Question 11.
Justify the statement, “Work and energy are the two sides of a coin”.
Answer:
- Work and energy both are scalar quantities.
- Work and energy both have the same dimensions i.e., [M1L2T-2].
- Work and energy both have the same units i.e., SI unit: joule and CGS unit: erg.
- Energy refers to the total amount of work a body can do.
- A body capable of doing more work possesses more energy and vice versa.
- Work done on a body by a conservative force is equal to the change in its kinetic energy.
Thus, work and energy are the two sides of the same
![]()
Question 12.
From the terrace of a building of height H, you dropped a ball of mass m. It reached the ground with speed v. Is the relation mgH = \(\frac{1}{2} m \mathrm{v}^{2}\) applicable exactly? If not, how can you account for the difference? Will the ball bounce to the same height from where it was dropped?
Answer:
- Let the ball dropped from the terrace of a building of height h have mass m. During free fall, the ball is acted upon by gravity (accelerating conservative force).
- While coming down, the work that is done is equal to the decrease in the potential energy.
- This work done however is not entirely converted into kinetic energy but some part of it is used in overcoming the air resistance (retarding non-conservative force). This part of energy appears in some other forms such as heat, sound, etc.
- Thus, in this case of an accelerating conservative force along with a retarding non-conservative force, the work-energy theorem is given as, Decrease in the gravitational
P.E. = Increase in the kinetic energy + work done against non-conservative forces. - Thus, the relation mgh = \(\frac{1}{2} \mathrm{mv}^{2}[latex] is not applicable when non-conservative forces are considered. The part of the energy converted to heat, sound etc also needs to be added to the equation,
- The ball will not bounce to the same height from where it was dropped due to the loss in kinetic energy during the collision making it an inelastic collision.
Question 13.
State the law of conservation of linear momentum. It is a consequence of which law? Given an example from our daily life for conservation of momentum. Does it hold good during burst of a cracker?
Answer:
- Statement: The total momentum of an isolated system is conserved during any interaction.
- The law of conservation of linear momentum is a consequence of Newton’s second law of motion, (in combination with Newton’s third law)
- Example: When a nail is driven into a wall by striking it with a hammer, the hammer is seen to rebound after striking the nail. This is because the hammer imparts a certain amount of momentum to the nail and the nail imparts an equal and opposite amount of momentum to the hammer.
Linear momentum conservation during the burst of a cracker:- The law of conservation of linear momentum holds good during bursting of a cracker.
- When a cracker is at rest before explosion, the linear momentum of the cracker is zero.
- When cracker explodes into number of pieces, scattered in different directions, the vector sum of linear momentum of these pieces is also zero. This is as per the law of conservation of linear momentum.
Question 14.
Define coefficient of restitution and obtain its value for an elastic collision and a perfectly inelastic collision.
Answer:
i. For two colliding bodies, the negative of ratio of relative velocity of separation to relative velocity of approach is called the coefficient of restitution.
ii. Consider an head-on collision of two bodies of masses m1 and m2 with respective initial velocities u1 and u2. As the collision is head on, the colliding masses are along the same line before and after the collision. Relative velocity of approach is given as,
ua = u2 – u1
Let v1 and v2 be their respective velocities after the collision. The relative velocity of recede (or separation) is then vs = v2 – v1
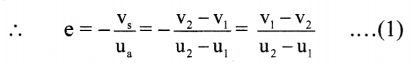
iii. For a head on elastic collision, According to the principle of conservation of linear momentum,
Total initial momentum = Total final momentum

iv. For a perfectly inelastic collision, the colliding bodies move jointly after the collision, i.e., v1 = v2
∴ v1 – v2 = 0
Substituting this in equation (1), e = 0.
![]()
Question 15.
Discuss the following as special cases of elastic collisions and obtain their exact or approximate final velocities in terms
of their initial velocities.
(i) Colliding bodies are identical.
(ii) A very heavy object collides on a lighter object, initially at rest.
(iii) A very light object collides on a comparatively much massive object, initially at rest.
Answer:
The final velocities after a head-on elastic collision is given as,
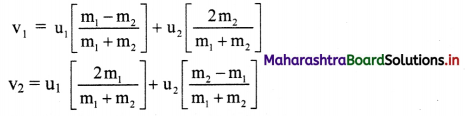
i. Colliding bodies are identical
If m1 = m2, then v1 = u2 and v2 = u1
Thus, objects will exchange their velocities after head on elastic collision.
ii. A very heavy object collides with a lighter object, initially at rest.
Let m1 be the mass of the heavier body and m2 be the mass of the lighter body i.e., m1 >> m2; lighter particle is at rest i.e., u2 = 0 then,
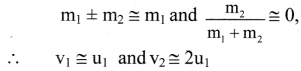
i.e., the heavier colliding body is left unaffected and the lighter body which is struck, travels with double the speed of the massive striking body.
iii. A very light object collides on a comparatively much massive object, initially at rest.
If m1 is mass of a light body and m2 is mass of heavy body i.e., m1 << m2 and u2 = 0. Thus, m1 can be neglected.
Hence v1 ≅ -u1, and v2 ≅ 0.
i.e., the tiny (lighter) object rebounds with same speed while the massive object is unaffected.
Question 16.
A bullet of mass m1 travelling with a velocity u strikes a stationary wooden block of mass m2 and gets embedded into it. Determine the expression for loss in the kinetic energy of the system. Is this violating the principle of conservation of energy? If not, how can you account for this loss?
Answer:
- A bullet of mass m1 travelling with a velocity u, striking a stationary wooden block of mass m2 and getting embedded into it is a case of perfectly inelastic collision.
- In a perfectly inelastic collision, although there is a loss in kinetic energy, the principle of conservation of energy is not violated as the total energy of the system is conserved.
Loss in the kinetic energy during a perfectly inelastic head on collision:
- Let two bodies A and B of masses m1 and m2 move with initial velocity [latex]\overrightarrow{\mathrm{u}_{1}}\), and \(\overrightarrow{\mathrm{u}_{2}}\) respectively such that particle A collides head- on with particle B i.e., u1 > u2.
- If the collision is perfectly inelastic, the particles stick together and move with a common velocity \(\overrightarrow{\mathbf{V}}\) after the collision along the same straight line.
loss in kinetic energy = total initial kinetic energy – total final kinetic energy, - By the law of conservation of momentum, m1u1 + m2u2 = (m1 + m2) v
∴ v = \(\frac{\mathrm{m}_{1} \mathrm{u}_{1}+\mathrm{m}_{2} \mathrm{u}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\) - Loss of Kinetic energy,
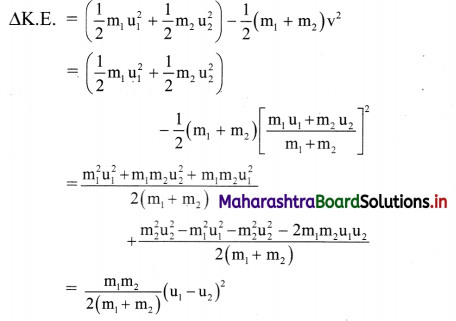
- Both the masses and the term (u1 – u2)2 are positive. Hence, there is always a loss in a perfectly inelastic collision. For a perfectly inelastic collision, as e = 0, the loss is maximum.
Question 17.
One of the effects of a force is to change the momentum. Define the quantity related to this and explain it for a variable
force. Usually when do we define it instead of using the force?
Answer:
- Impulse is the quantity related to change in momentum.
- Impulse is defined as the change of momentum of an object when the object is acted upon by a force for a given time interval.
Need to define impulse:
- In cases when time for which an appreciable force acting on an object is extremely small, it becomes difficult to measure the force and time independently.
- In such cases, however, the effect of the force i.e, the change in momentum due to the force is noticeable and can be measured.
- For such cases, it is convenient to define impulse itself as a physical quantity.
- Example: Hitting a ball with a bat, giving a kick to a foot-ball, hammering a nail, bouncing a ball from a hard surface, etc.
Impulse for a variable force:
- Consider the collision between a bat and ball. The variation of the force as a function of time is shown below. The force axis is starting from zero.
- From the graph, it can be seen that the force is zero before the impact. It rises to a maximum during the impact and decreases to zero after the impact.
- The shaded area or the area under the curve of the force -time graph gives the product of force against the corresponding time (∆t) which is the impulse of the force.
Area of ABCDE = F. ∆t = impulse of force - For a constant force, the area under the curve is a rectangle.
- In case of a softer tennis ball, the collision time becomes larger and the maximum force becomes less keeping the area under curve of the (F – t) graph same.
Area of ABCDE = Area of PQRST
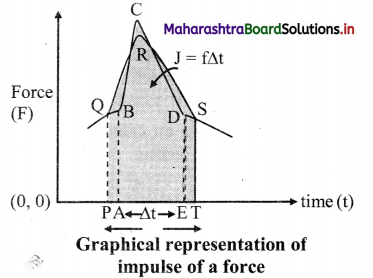
In chapter 3, you have studied the concept of using area under the curve.
![]()
Question 18.
While rotating an object or while opening a door or a water tap we apply a force or forces. Under which conditions is this process easy for us? Why? Define the vector quantity concerned. How does it differ for a single force and for two opposite forces with different lines of action?
Answer:
- Opening a door can be done with ease if the force applied is:
- proportional to the mass of the object
- far away from the axis of rotation and the direction of force is perpendicular to the line joining the axis of rotation with the point of application of force.
- This is because, the rotational ability of a force depends not only upon the magnitude and direction of force but also on the point where the force acts with respect to the axis of rotation.
- Rotating an object like a water tap can be done with ease if the two forces are equal in magnitude but opposite in direction are applied along different lines of action.
- The ability of a force to produce rotational motion is measured by its turning effect called ‘moment of force’ or ‘torque’.
- However, a moment of couple or rotational effect of a couple is also called torque.
- For differences in the two vector quantities.
| No. | Moment of a force | Moment of a couple |
| i. | Moment of a force is given as, \(\vec{\tau}=\vec{r} \times \vec{F}\) | Moment of a couple is given as, \(\vec{\tau}=\vec{r}_{12} \times \vec{F}_{1}=\vec{r}_{21} \times \vec{F}_{2}\) |
| ii. | It depends upon the axis of rotation and the point of application of the force. | It depends only upon the two forces, i.e., it is independent of the axis of rotation or the points of application of forces. |
| iii. | It can produce translational acceleration also, if the axis of rotation is not fixed or if friction is not enough. | Does not produce any translational acceleration, but produces only rotational or angular acceleration. |
| iv. | Its rotational effect can be balanced by a proper single force or by a proper couple. | Its rotational effect can be balanced only by another couple of equal and opposite torque. |
Question 19.
Why is the moment of a couple independent of the axis of rotation even if the axis is fixed?
Answer:
- Consider a rectangular sheet free to rotate only about a fixed axis of rotation, perpendicular to the plane.
- A couple of forces \(\overrightarrow{\mathrm{F}}\) and –\(\overrightarrow{\mathrm{F}}\) is acting on the sheet at two different locations.
- Consider the torque of the couple as two torques due to individual forces causing rotation about the axis of rotation.
- Case 1: The axis of rotation is between the lines of action of the two forces constituting the couple. Let x and y be the perpendicular distances of the axis of rotation from the forces \(\overrightarrow{\mathrm{F}}\) and –\(\overrightarrow{\mathrm{F}}\) respectively.
In this case, the pair of forces cause anticlockwise rotation. As a result, the direction of individual torques due to the two forces is the same.
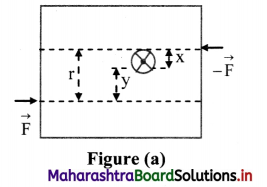
- Case 2: Lines of action of both the forces are on the same side of the axis of rotation. Let q and p be the perpendicular distances of the axis of rotation from the forces \(\overrightarrow{\mathrm{F}}\) and –\(\overrightarrow{\mathrm{F}}\)
Question 20.
Explain balancing or mechanical equilibrium. Linear velocity of a rotating fan as a whole is generally zero. Is it in
mechanical equilibrium? Justify your answer.
Answer:
- The state in which the momentum of a system is constant in the absence of an external unbalanced force is called mechanical equilibrium.
- A particle is said to be in mechanical equilibrium, if no net force is acting upon it.
- In case of a system of bodies to be in mechanical equilibrium, the net force acting on any part of the system should be zero i.e., the velocity or linear momentum of all parts of the system must be constant or zero. There should be no acceleration in any part of the system.
- Mathematically, for a system in mechanical equilibrium, \(\sum \vec{F}\) = 0.
- In case of rotating fan, if linear velocity is zero, then the linear momentum is zero. That means there is no net force acting on the fan. Hence, the fan is in mechanical equilibrium.
Question 21.
Why do we need to know the centre of mass of an object? For which objects, its position may differ from that of the centre of gravity?
Use g = 10 m s-2, unless, otherwise stated.
Answer:
- Centre of mass of an object allows us to apply Newton’s laws of motion to finite objects (objects of measurable size) by considering these objects as point objects.
- For objects in non-uniform gravitational field or whose size is comparable to that of the Earth (size at least few thousand km), the position of centre of mass will differ than that of centre of gravity.
3. Solve the following problems.
Question 1.
A truck of mass 5 ton is travelling on a horizontal road with 36 km hr-1 stops on travelling 1 km after its engine fails suddenly. What fraction of its weight is the frictional force exerted by the road? If we assume that the story repeats for a car of mass 1 ton i.e., can moving with same speed stops in similar distance same how much will the fraction be?
[Ans: \(\frac{1}{200}\) in the both]
Solution:
Given: mtruck = 5 ton = 5000 kg,
mcar = 1 ton = 1000 kg,
u = 36km/hr = 10 m/s,
v = 0 m/s, s = 1 km = 1000 m
To find: Ratio of force of friction to the weight of vehicle
Formulae:
i. v2 = u2 + 2as
ii. F = ma
Calculation: From formula (i),
2 × atruck × s = v2 – u2
∴ 2 × atruck × 1000 = 02 – 102
∴ 200atruck = -100
∴ atruck = -0.05 m/s2
Negative sign indicates that velocity is decreasing
From formula (ii),
Ftruck = mtruck × atruck = 5000 × 0.05
= 250 N

Answer:
The frictional force acting on both the truck and the car is \(\frac{1}{200}\) of their weight.
![]()
Question 2.
A lighter object A and a heavier object B are initially at rest. Both are imparted the same linear momentum. Which will start with greater kinetic energy: A or B or both will start with the same energy?
[Ans: A]
Solution:
- Let m1 and m2 be the masses of light object A and heavy object B and v1 and v2 be their respective velocities.
- Since both are imparted with the same linear momentum,
m1 v1 = m2 v2 - Kinetic energy of the lighter object A

- As m1 < m2, therefore K.E.A > K.E.B, i.e, the lighter body A has more kinetic energy.
Question 3.
As i was standing on a weighing machine inside a lift it recorded 50 kg wt. Suddenly for few seconds it recorded 45 kg wt. What must have happened during that time? Explain with complete numerical analysis. [Ans: Lift must be coming down with acceleration \(\frac{\mathrm{g}}{10}\) = 1 ms-2]
Solution:
The weight recorded by weighing machine is always apparent weight and a measure of reaction force acting on the person. As the apparent weight (45 kg-wt) in this case is less than actual weight (50 kg-wt) the lift must be accelerated downwards during that time.
Numerical Analysis
- Weight on the weighing machine inside the lift is recorded as 50 kg-wt
∴ mg = 50 kg-wt
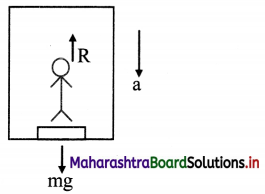
- This weight acts on the weighing machine which offers a reaction R given by the reading of the weighing machine
∴ R = 45kg-wt = \(\frac{9}{10}\)mg - The forces acting on person inside lift are as follows:
- Weight mg downward (exerted by the earth)
- Normal reaction (R) upward (exerted by the floor)
- As, R < mg, the net force is in downward direction and given as,
mg – R=ma
But R = \(\frac{9}{10}\)mg.
∴ mg – \(\frac{9}{10}\)mg = ma
∴ \(\frac{mg}{10}\) = ma
∴ a = g/10
∴ a = 1 m/s2 (∵ g = 1 m/s2) - Therefore, the elevator must be accelerated downwards with an acceleration of 1 m/s2 at that time.
Question 4.
Figure below shows a block of mass 35 kg resting on a table. The table is so rough that it offers a self adjusting resistive force 10% of the weight of the block for its sliding motion along the table. A 20 kg wt load is attached to the block and is passed over a pulley to hang freely on the left side. On the right side there is a 2 kg wt pan attached to the block and hung freely. Weights of 1 kg wt each, can be added to the pan. Minimum how many and maximum how many such weights can be added into the pan so that the block does not slide along the table? [Ans: Min 15, maximum 21].
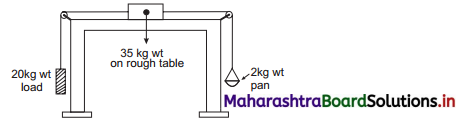
Solution:
Frictional (resistive) force f = 10% (weight)
= \(\frac{10}{100}\) × 35 × 10 = 35N 100
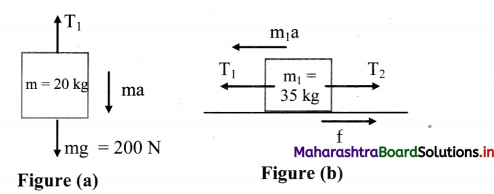
i. Consider FBD for 20 kg-wt load. Initially, the block kept on the table is moving towards left, because of the movement of block of mass 20 kg in downward direction.
Thus, for block of mass 20 kg,
ma = mg – T1 …. (1)
Consider the forces acting on the block of mass 35 kg in horizontal direction only as shown in figure (b). Thus, the force equation for this block is, m1a = T1 – T2 – f ….(2)
To prevent the block from sliding across the table,
m1a = ma = 0
∴ T1 = mg = 200 N ….[From (1)]
T1 = T2 + f ….[From (2)]
∴ T2 + f = 200
∴ T2 = 200 – 35 = 165 N
Thus, the total force acting on the block from right hand side should be 165 N.
∴ Total mass = 16.5 kg
∴ Minimum weight to be added = 16.5 – 2 = 14.5 kg
≈ 15 weights of 1 kg each
ii. Now, considering motion of the block towards right, the force equations for the masses in the pan and the block of mass 35 kg can be determined from FBD shown
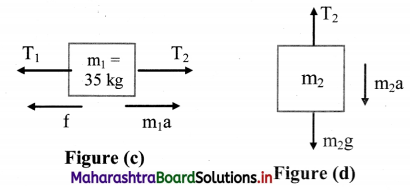
From figure (c)
m1a = T2 – T1 – f ….(iii)
From figure (d),
m2a = m2g – T2 … .(iv)
To prevent the block of mass 35 kg from sliding across the table, m1a = m2a = 0
From equations (iii) and (iv),
T2 = T1 + f
T2 = m2g
∴ m2g = 200 + 35 = 235 N
∴ The maximum mass required to stop the sliding = 23.5 – 2 = 21.5kg ≈ 21 weights of 1 kg
Answer:
The minimum 15 weights and maximum 21 weights of 1 kg each are required to stop the block from sliding.
Question 5.
Power is rate of doing work or the rate at which energy is supplied to the system. A constant force F is applied to a body
of mass m. Power delivered by the force at time t from the start is proportional to
(a) t
(b) t2
(c) \(\sqrt{t}\)
(d) t0
Derive the expression for power in terms of F, m and t.
[Ans: p = \(\frac{F^{2} t}{m}\), ∴ p ∝ t]
Solution:
Derivation for expression of power:
i. A constant force F is applied to a body of mass (m) initially at rest (u = 0).
ii. We have,
v = u + at
∴ v = 0 + at
∴ v = at …. (1)
iii. Now, power is the rate of doing work,
∴ P = \(\frac{\mathrm{d} \mathrm{W}}{\mathrm{d} \mathrm{t}}\)
∴ P = F. \(\frac{\mathrm{d} \mathrm{s}}{\mathrm{dt}}\) [∵ dW = F. ds]
iv. But \(\frac{\mathrm{d} \mathrm{s}}{\mathrm{dt}}\) = v, the instantaneous velocity of the particle.
∴ P = F.V … (2)
v. According to Newton’s second law,
F = ma … (3)
vi. Substituting equations (1) and (3) in equation (2)
P = (ma) (at)
∴ P = ma2t
∴ P = \(\frac{m^{2} a^{2}}{m}\) × t
∴ P = \(\frac{\mathrm{F}^{2}}{\mathrm{~m}} \mathrm{t}\)
vii. As F and m are constant, therefore, P ∝ t.
![]()
Question 6.
40000 litre of oil of density 0.9 g cc is pumped from an oil tanker ship into a storage tank at 10 m higher level than the ship in half an hour. What should be the power of the pump? [Ans: 2 kW]
Solution:
h = 10 m, ρ = 0.9 g/cc = 900 kg/m3, g = 10 m/s2,
V = 40000 litre = 40000 × 103 × 10-6 m3
= 40 m3
T = 30 min = 1800 s
To find: Power(P)
Formula: P = \(\frac{\mathrm{W}}{\mathrm{t}}=\frac{\mathrm{h} \rho \mathrm{gV}}{\mathrm{t}}\)
Calculation: From formula,
P = \(\frac{10 \times 900 \times 10 \times 40}{1800}\)
∴ P = 2000 W
∴ P = 2 kW
Answer:
The power of the pump is 2 kW.
Question 7.
Ten identical masses (m each) are connected one below the other with 10 strings. Holding the topmost string, the system is accelerated upwards with acceleration g/2. What is the tension in the 6th string from the top (Topmost string being the first string)? [Ans: 6 mg]
Solution
Consider the 6th string from the top. The number of masses below the 6th string is 5. Thus, FBD for the 6th mass is given in figure (b).
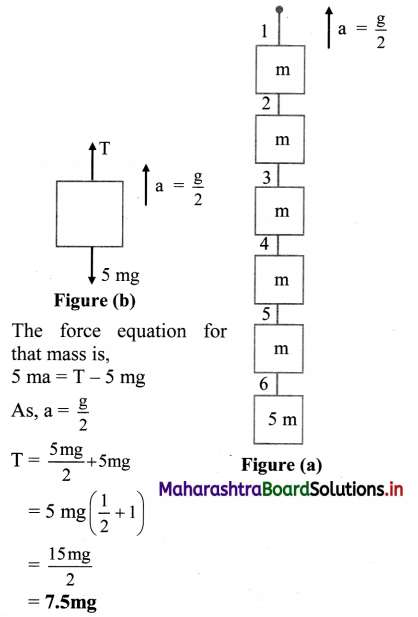
Answer:
Tension in the 6th string is 7.5 mg.
[Note: The answer given above is modified considering the correct textual concepts.]
Question 8.
Two galaxies of masses 9 billion solar mass and 4 billion solar mass are 5 million light-years apart. If, the Sun has to cross the line joining them, without being attracted by either of them, through what point it should pass? [Ans: 3 million light-years from the 9 billion solar mass]
Solution:
The Sun can cross the line joining the two galaxies without being attracted by either of them if it passes from a neutral point. A neutral point is a point on the line joining two objects where the effect of gravitational forces acting due to both the objects is nullified.
Given that;
m1 = 9 × 109 Ms
m2 = 4 × 109 Ms
r = 5 × 106 light years
Let the neutral point be at distance x from mi. If sun is present at that point,

Answer: The Sun has to cross the line from a point at a distance 3 million light years from the galaxy of mass 9 billion solar mass.
Question 9.
While decreasing linearly from 5 N to 3 N, a force displaces an object from 3 m to 5 m. Calculate the work done by this force during this displacement. [Ans: 8 N]
Solution:
For a variable force, work done is given by area under the curve of force v/s displacement graph. From given data, graph can be plotted as follows:
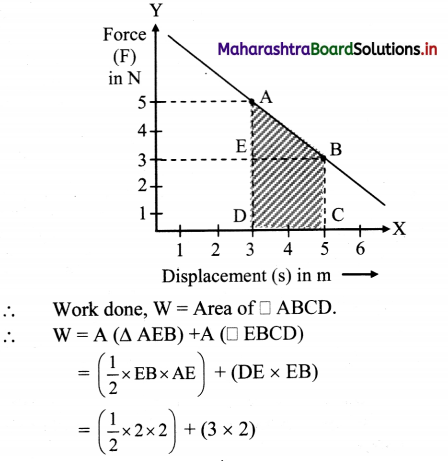
= 8 J
Ans: Work done is 8 J.
[Note: According to the definition of work done, S.J. unit of wõrk done is joule (J)]
Alternate solution:
Work done, w = Area of trapezium ADCB
∴ W = \(\frac{1}{2}\)(AD + CB) × DC
∴ W = 1 (5N + 3N) × (5m – 3m)
= \(\frac{1}{2}\) × 8 × 2 = 8J
![]()
Question 10.
Variation of a force in a certain region is given by F = 6x2 – 4x – 8. It displaces an object from x = 1 m to x = 2 m in this region. Calculate the amount of work
done. [Ans: Zero]
Solution:
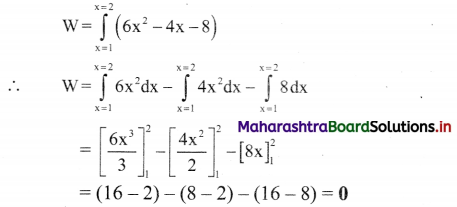
Answer:
The work done is zero.
Question 11.
A ball of mass 100 g dropped on the ground from 5 m bounces repeatedly. During every bounce 64% of the potential energy is converted into kinetic energy. Calculate the following:
(a) Coefficient of restitution.
(b) Speed with which the ball comes up from the ground after third bounce.
(c) Impulse given by the ball to the ground during this bounce.
(d) Average force exerted by the ground if this impact lasts for 250 ms.
(e) Average pressure exerted by the ball on the ground during this impact if the contact area of the ball is 0.5 cm2.
[Ans: 0.8, 5.12 m/s, 1.152N s, 4.608 N, 9.216 × 104 N/m2]
Solution:
Given that, for every bounce, 64% of the initial energy is converted to final energy.
i. Coefficient of restitution in case of inelastic collision is given by,

ii. From equation (1),
∴ v = – eu
∴ After first bounce,
v1 = – eu
after second bounce,
v2 = -ev1 = -e(-eu)= e2u
and after third bounce,
v3 = – ev2 = – e(e2u) = – e3u
But u = \(\sqrt{2 \mathrm{gh}}\)
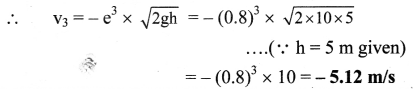
iii. Impulse given by the ball during third bounce, is,
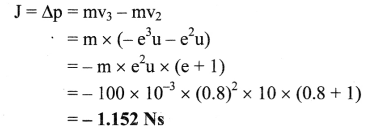
iv. Average force exerted in 250 ms,

v. Average pressure for area
0.5 cm2 = 0.5 × 10-4m2
P = \(\frac{\mathrm{F}}{\mathrm{A}}=\frac{4.608}{0.5 \times 10^{-4}}\) = 9.216 × 104 N/m2
Question 12.
A spring ball of mass 0.5 kg is dropped from some height. On falling freely for 10 s, it explodes into two fragments of
mass ratio 1:2. The lighter fragment continues to travel downwards with speed of 60 m/s. Calculate the kinetic energy supplied during explosion. [Ans: 200 J]
Solution:
m1 + m2 = 0.5 kg, m1 : m2 = 1 : 2,
m1 = \(\frac{1}{6}\) kg,
∴ m2 = \(\frac{1}{3}\) kg
Initially, when the ball is falling freely for 10s,
v = u + at = 0 + 10(10)
∴ v = 100 m/s = u1 = u2
(m1 + m2)v = m1v1 + m2v2
∴ 0.5 × 100 = \(\frac{1}{6}\)(60) + \(\frac{1}{3}\)v2
∴ 50 = 10 + \(\frac{1}{3}\)v2
∴ 40 = \(\frac{1}{3}\)v2
∴ v2 = 120m/s
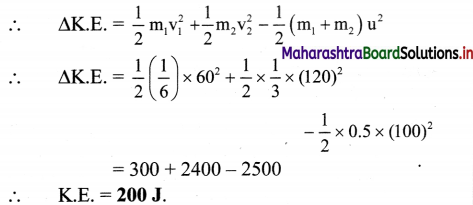
∴ K.E. = 200J.
Ans: Kinetic energy supplied is 200 J.
Question 13.
A marble of mass 2m travelling at 6 cm/s is directly followed by another marble of mass m with double speed. After collision, the heavier one travels with the average initial speed of the two. Calculate the coefficient of restitution. [Ans: 0.5]
Solution:
Given: m1 = 2m, m2 = m, u1 = 6 cm/s,
u2 = 2u1 = 12 cm/s,
v1 = \(\frac{\mathrm{u}_{1}+\mathrm{u}_{2}}{2}\) = 9cm/s
To find: Coefficient of restitution(e)
Formulae:
i. m1u1 +m2u2 = m1v1 + m2v2
ii. e = \(\frac{v_{2}-v_{1}}{u_{1}-u_{2}}\)
Calculation: From formula (i),
[(2m) × 6] + (m × 12) = (2m × 9) + mv2
∴ v2 = 6cm/s
From formula (ii),
e = \(\frac{6-9}{6-12}\) = \(\frac{-3}{-6}\) = 0.5
Answer: The coefficient of restitution is 0.5
![]()
Question 14.
A 2 m long wooden plank of mass 20 kg is pivoted (supported from below) at 0.5 m from either end. A person of mass 40 kg starts walking from one of these pivots to the farther end. How far can the person walk before the plank topples? [Ans: 1.25 m]
Solution:
Let the person starts walking from pivot P2 as shown in the figure.
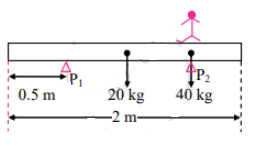
Assume the person can walk up to distance x from P1 before the plank topples. The plank will topple when the moment exerted by the person about P1 is not balanced by a moment of force due to plank about P2.
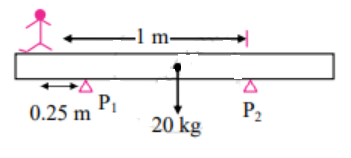
∴ For equilibrium,
40 × x = 20 × 0.5
∴ x = \(\frac{1}{4}\) = 0.25 m
Hence, the total distance walked by the person is 1.25 m.
Question 15.
A 2 m long ladder of mass 10 kg is kept against a wall such that its base is 1.2 m away from the wall. The wall is smooth but the ground is rough. The roughness of the ground is such that it offers a maximum horizontal resistive force (for sliding motion) half that of normal reaction at the point of contact. A monkey of mass 20 kg starts climbing the ladder. How far can it climb along the ladder? How much is the horizontal reaction at the wall? [Ans: 1.5 m, 15 N]
Solution:
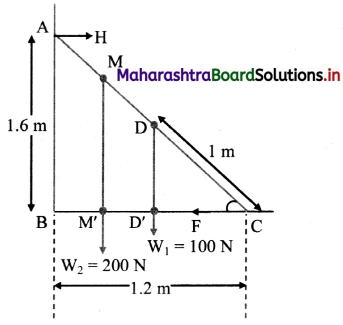
From the figure,
Given that, AC = length of ladder = 2 m
BC= 1.2m
From Pythagoras theorem,
AB = \(\sqrt{\mathrm{AC}^{2}-\mathrm{BC}^{2}}\) = 1.6 m … (i)
Also, ∆ABC ~ ∆DD’C
∴ \(\frac{\mathrm{AB}}{\mathrm{DD}^{\prime}}\) = \(\frac{\mathrm{BC}}{\mathrm{D}^{\prime} \mathrm{C}}\) = \(\frac{\mathrm{AC}}{\mathrm{DC}}\)
∴ \(\frac{1.2}{\mathrm{D}^{\prime} \mathrm{C}}=\frac{2}{1}\)
∴ D’C = 0.6 m … (ii)
The ladder exerts horizontal force \(\overrightarrow{\mathrm{H}}\) on the wall at A and \(\overrightarrow{\mathrm{F}}\) is the force exerted on the ground at C.
As |\(\overrightarrow{\mathrm{F}}\)| = \(|\overrightarrow{\mathrm{H}}|=|\overrightarrow{\mathrm{F}}|=\frac{\mathrm{N}}{2}\) … (iii)
Let monkey climb upto distance x along BC (Horizontal) i.e., CM’ = x .. . .(iv)
Then, the net normal reaction at point C will be, N = 100 + 200 = 300N
From equation (iii),
H = \(\frac{\mathrm{N}}{2}=\frac{300}{2}\) = 150N
By condition of equilibrium, taking moments about C,
(-H × AB) + (W1 × CD’) + (W2 × CM’) + (F × 0)’0
∴ (-150 × 1.6) + (100 × 0.6) + (200 × x) = 0
∴ 60 + 200x = 240
∴ 200x = 180
∴ x = 0.9
From figure, it can be shown that,
∆ABC ~ ∆MM’C
∴ \(\frac{\mathrm{BC}}{\mathrm{CM}^{\prime}}\) = \(\frac{\mathrm{AC}}{\mathrm{CM}^{\prime}}\) ∴ \(\frac{\mathrm{1.2}}{\mathrm{0.9}^{\prime}}\) = \(\frac{\mathrm{2}}{\mathrm{CM}^{\prime}}\)
∴ CM = 1.5 m
Answer:
- The monkey can climb upto 1.5 m along the ladder.
- The horizontal reaction at wall is 150 N.
Question 16.
Four uniform solid cubes of edges 10 cm, 20 cm, 30 cm and 40 cm are kept on the ground, touching each other in order. Locate centre of mass of their system. [Ans: 65 cm, 17.7 cm]
Solution:
The given cubes are arranged as shown in figure. Let one of the comers of smallest cube lie at the origin.
As the cubes are uniform, let their centre of masses lie at their respective centres.
rA \(\equiv\) (5, 5), rB \(\equiv\) (20, 10), rC \(\equiv\) = (45, 15) and rD \(\equiv\) – (80, 20)
Also, masses of the cubes are,
mA = \(l_{\mathrm{A}}^{3} \times \rho=10^{3} \rho\)
mB = (20)3ρ
mC = (30)3ρ
mD = (40)3ρ
As the cubes are uniform, p is same for all of them.
∴ For X – co-ordinate of centre of mass of the system,

Similarly,
Y – co-ordinate of centre of mass of system is,

Answer: Centre of mass of the system is located at point (65 cm, 17.7 cm)
![]()
Question 17.
A uniform solid sphere of radius R has a hole of radius R/2 drilled inside it. One end of the hole is at the centre of the
sphere while the other is at the boundary. Locate centre of mass of the remaining sphere. [Ans: -R/14 ]
Solution:
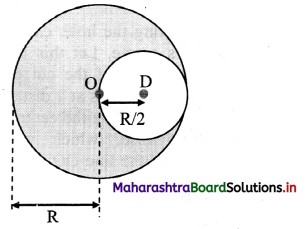
Let the centre of the sphere be origin O. Then, r1 be the position vector of centre of mass of uniform solid sphere and r2 be the position vector of centre of mass of the cut-out part of the sphere.
Now, mass of the sphere is given as,

∴ Position vector of centre of mass of remaining part,
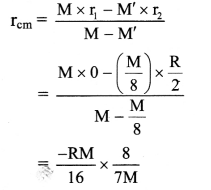
rCM = \(\frac{-\mathbf{R}}{14}\)
(Negative sign indicates the distance is on left side of the origin.)
Ans: Position of centre of mass of remaining sphere \(\frac{-\mathbf{R}}{14}\)
Question 18.
In the following table, every item on the left side can match with any number of items on the right hand side. Select all those.

Answer:
i. Elastic collision: (b)
ii. Inelastic collision: (a), (c), (f), (e)
iii. Perfectly inelastic collision: (d)
iv. Head-on collision: (c), (f)
11th Physics Digest Chapter 4 Laws of Motion Intext Questions and Answers
Can you recall? (Textbook Page No. 47)
Question 1.
What are different types of motions?
Answer:
The various types of motion are linear, uniform linear, non-uniform linear, oscillatory, circular, periodic, and random motion.
Question 2.
What do you mean by kinematical equations and what are they?
Answer:
A set of three equations that analyses rectilinear motion of the uniformly accelerated body and help to predict the position of body are called kinematical equations.
- Equation for velocity-time relation: v = u + at
- Equation for position-time relation: s = ut + \(\frac{1}{2}\)at2
- Position-velocity relation: v2 = u2 + 2as
Can you tell? (Textbook Page No. 48)
Question 1.
Was Aristotle correct? If correct, explain his statement with an illustration.
Answer:
Aristotle was not correct in stating that an external force is required to keep a body in uniform motion.
Question 2.
If wrong, give the correct modified version of his statement.
Answer:
For an uninterrupted motion of a body, an additional external force is required for overcoming opposing/resistive forces.
![]()
Can you tell? (Textbook Page No. 48)
Question 1.
What is then special about Newton’s first law if it is derivable from Newton’s second law?
Answer:
- Newton’s first law shows an equivalence between the ‘state of rest’ and ‘state of uniform motion along a straight line.’
- Newton’s first law of motion defines force as a physical quantity that brings about a change in ‘state of rest’ or ‘state of .uniform motion along a straight line’ of a body.
- Newton’s first law of motion defines inertia as a fundamental property of every physical object by which the object resists any change in its state of rest or of uniform motion along a straight line.
- Due to all these reasons, Newton’s first law should be studied.