Maharashtra Board Class 12 Chemistry Solutions Chapter 2 Solutions

Balbharti Maharashtra State Board 12th Chemistry Textbook Solutions Chapter 2 Solutions Textbook Exercise Questions and Answers.

Maharashtra State Board 12th Chemistry Solutions Chapter 2 Solutions

1. Choose the most correct answer.

Question i.
The vapour pressure of a solution containing 2 moles of a solute in 2 moles of water (vapour pressure of pure water = 24 mm Hg) is
(a) 24 mm Hg
(b) 32 mm Hg
(c) 48 mm Hg
(d) 12 mm Hg
Answer:
(d) 12 mm Hg

Question ii.
The colligative property of a solution is
(a) vapour pressure
(b) boiling point
(c) osmotic pressure
(d) freezing point
Answer:
(c) osmotic pressure

Question iii.
In calculating osmotic pressure the concentration of solute is expressed in
(a) molarity
(b) molality
(c) mole fraction
(d) mass per cent
Answer:
(a) molarity

Question iv.
Ebullioscopic constant is the boiling point elevation when the concentration of solution is
(a) 1 m
(b) 1 M
(c) 1 mass%
(d) 1 mole fraction of solute
Answer:
(a) 1 m

Question v.
Cryoscopic constant depends on
(a) nature of solvent
(b) nature of solute
(c) nature of solution
(d) number of solvent molecules
Answer:
(a) nature of solvent

Question vi.
Identify the correct statement
(a) vapour pressure of solution is higher than that of pure solvent.
(b) boiling point of solvent is lower than that of solution
(c) osmotic pressure of solution is lower than that of solvent
(d) osmosis is a colligative property.
Answer:
(b) boiling point of solvent is lower than that of solution

Question vii.
A living cell contains a solution which is isotonic with 0.3 M sugar solution. What osmotic pressure develops when the cell is placed in 0.1 M KCl solution at body temperature ?
(a) 5.08 atm
(b) 2.54 atm
(c) 4.92 atm
(d) 2.46 atm
Answer:
(c) 4.92 atm

Question viii.
The osmotic pressure of blood is 7.65 atm at 310 K. An aqueous solution of glucose isotonic with blood has the percentage (by volume)
(a) 5.41%
(b) 3.54%
(c) 4.53%
(d) 53.4%
Answer:
(a) 5.41%

Question ix.
Vapour pressure of a solution is
(a) directly proportional to the mole fraction of the solute
(b) inversely proportional to the mole fraction of the solute
(c) inversely proportional to the mole fraction of the solvent
(d) directly proportional to the mole fraction of the solvent
Answer:
(d) directly proportional to the mole fraction of the solvent

Question x.
Pressure cooker reduces cooking time for food because
(a) boiling point of water involved in cooking is increased
(b) heat is more evenly distributed in the cooking space
(c) the higher pressure inside the cooker crushes the food material
(d) cooking involves chemical changes helped by a rise in temperature
Answer:
(a) boiling point of water involved in cooking is increased

Question xi.
Henry’s law constant for a gas CH₃Br is 0.159 mol dm^-3 atm at 250°C. What is the solubility of CH₃Br in water at 25 °C and a partial pressure of 0.164 atm?
(a) 0.0159 mol L^-1
(b) 0.164 mol L^-1
(c) 0.026 M
(d) 0.042 M
Answer:
(c) 0.026 M

Question xii.
Which of the following statement is NOT correct for 0.1 M urea solution and 0.05 M sucrose solution ?
(a) osmotic pressure exhibited by urea solution is higher than that exhibited by sucrose solution
(b) urea solution is hypertonic to sucrose solution
(c) they are isotonic solutions
(d) sucrose solution is hypotonic to urea solution
Answer:
(c) they are isotonic solutions

2. Answer the following in one or two sentences

Question i.
What is osmotic pressure ?
Answer:
(1) Definition : The osmotic pressure is defined as the excess mechanical pressure required to be applied to a solution separated by a semipermeable membrane from pure solvent or a dilute solution to prevent the osmosis or free passage of the solvent molecules at a given temperature. The osmotic pressure is a colligative property.

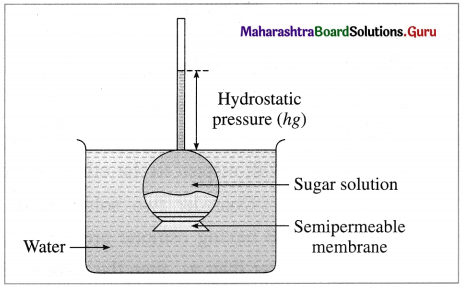
Osmosis and osmotic pressure

(2) Explanation : Consider an inverted thistle funnel on the mouth of which a semipermeable membrane is firmly fastened. It is filled with the experimental solution and immersed in a solvent like water. As a result, solvent molecules pass through the membrane into the solution in the funnel causing rising of level in the arm of thistle funnel. This increases the hydrostatic pressure. At a certain stage this rising level stops indicating an equilibrium between the rates of flow of solvent molecules from solvent to solution and from solution to solvent. The hydrostatic pressure at this stage represents osmotic pressure of the solution in the thistle funnel.

Question ii.
A solution concentration is expressed in molarity and not in molality while considering osmotic pressure. Why ?
Answer:

1. While calculating osmotic pressure by equation, π = CRT, the concentration is expressed in molarity but not in molality.
2. This is because the measurements of osmotic pressure are made at a certain constant temperature.
3. Molarity depends upon temperature but molality is independent of temperature.
4. Hence in osmotic pressure measurements, concentration is expressed in molarity.

Question iii.
Write the equation relating boiling point elevation to the concentration of solution.
Answer:
The elevation in the boiling point of a solution is directly proportional to the molal concentration (expressed in mol kg^-1) of the solution.
Hence, if ΔT_b is the elevation in the boiling point of a solution of molal concentration m then,
ΔT_b ∝ m
∴ ΔT_b = K_b m
where K_b is a proportionality constant.
If m = 1 molal,
ΔT_b = K_b
K_b is called the ebullioscopic constant or molal elevation constant. K_b is characteristic of the solvent.

Question iv.
A 0.1 m solution of K₂SO₄ in water has freezing point of -0.43 °C. What is the value of van’t Hoff factor if K_f for water is 1.86 K kg mol^-1?
Answer:
Given : m = 0.1 m, ΔT_f = 0 – (-0.43) = 0.43 °C
K_f = 1.86 K kg mol^-1, i = ?
ΔT_f = i × K_f × m
∴ i = \(\frac{\Delta T_{\mathrm{f}}}{K_{\mathrm{f}} \times m}=\frac{0.43}{1.86 \times 0.1}\) = 2.312
van’t Hoff factor = i = 2.312

Question v.
What is van’t Hoff factor?
Answer:
Definition of the van’t Hoff factor, i : It is defined as a ratio of the observed colligative property of the solution to the theoretically calculated colligative property of the solution without considering molecular change.

The van’t Hoff factor can be represented as,

This colligative property may be the lowering of vapour pressure of a solution, the osmotic pressure, the elevation in the boiling point or the depression in the freezing point of the solution. Hence,

• When the solute neither undergoes dissociation or association in the solution, then, i = 1
• When the solute undergoes dissociation in the solution, then, i > 1
• When the solute undergoes association in the solution, then i < 1

From the value of the van’t Hoff factor, the degree of dissociation of electrolytes, degree of association of nonelectrolytes can be obtained.

van’t Hoff factor gives the important information about the solute molecules in the solution and chemical bonding in them.

Question vi.
How is van’t Hoff factor related to degree of ionization?
Answer:
Consider 1 dm³ of a solution containing m moles of an electrolyte AxBy. The electrolyte on dissociation gives x number of A^y+ ions and y number of B^x- ions. Let α be the degree of dissociation.

At equilibrium,
AxBy ⇌ xA^y+ + yB^x-
For 1 mole of electrolyte : 1 – α,  xα,  yα
and For ‘m’ moles of an electrolyte : m(1 – α), mxα, myα are the number of particles.
Total number of moles at equilibrium, will be,
Total moles = m(1 – α) + mxα + myα
= m[(1 – α) + xα + yα]
= m[1 + xα + yα – α]
= m[1 + α(x + y – 1)]

The van’t Hoff factor i will be,

If total number of ions from one mole of electrolyte is denoted by n, then (x + y) = n
∴ i = 1 + α(n – 1)
∴ α(n – 1) = i – 1
∴ α = \(\frac{i-1}{n-1}\) ……(1)
This is a relation between van’t Hoff factor i and degree of dissociation of an electrolyte.

Question vii.
Which of the following solutions will have higher freezing point depression and why ?
a. 0.1 m NaCl b. 0.05 m Al₂(SO₄)₃
Answer:
(1) Freezing point depression is a colligative property, hence depends on the number of particles in the solution.
(2) More the number of particles in the solution, higher is the depression in freezing point.
(3) The number of particles (ions) from electrolytes are,

(4) Therefore Al₂(SO₄)₃ solution will have higher freezing point depression.

Question viii.
State Raoult’s law for a solution containing a nonvolatile solute.
Answer:
Statement of Raoult’s law : The law states that the vapour pressure of a solvent over the solution of a nonvolatile solute is equal to the vapour pressure of the pure solvent multiplied by mole fraction of the solvent at constant temperature.

Question ix.
What is the effect on the boiling point of water if 1 mole of methyl alcohol is added to 1 dm³ of water? Why?
Answer:

• The boiling point of water (or any liquid) depends on its vapour pressure.
• Higher the vapour pressure, lower is the boiling point.
• When 1 mole of volatile methyl alcohol is added to 1 dm³ of water, its vapour pressure is increased decreasing the boiling point of water.

Question x.
Which of the four colligative properties is most often used for molecular mass determination? Why?
Answer:

1. Since osmotic pressure has large values, it can be measured more precisely.
2. The osmotic pressure can be measured at a suitable constant temperature.
3. The molecular masses can be measured more accurately.
4. Therefore, it is more useful to determine molecular masses of expensive substances by osmotic pressure.

3. Answer the following.

Question i.
How vapour pressure lowering is related to a rise in boiling point of solution?
Answer:
(1) The boiling point of a liquid is the temperature at which the vapour pressure of the liquid becomes equal to the external pressure, generally 1 atm (101.3 × 10³ Nm^-2).

(2) When a liquid is heated, its vapour pressure rises till it becomes equal to the external pressure.
If the liquid has a low vapour pressure, it has a higher boiling point.

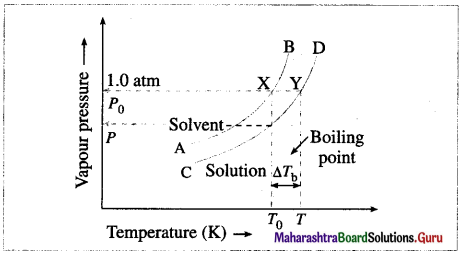
Vapour pressure curve showing elevation in boiling point

(3) When a nonvolatile solute is added to a solvent, its vapour pressure decreases, hence the boiling point increases.
This is explained by graphical representation of the vapour pressure and the boiling point of the pure solvent and the solution.

If T₀ and T are the boiling points of a pure solvent and a solution, then the elevation in the boiling point is given by,
ΔT_b = T – T₀
The curve AB, represents the variation in the vapour pressure of a pure solvent with temperature while curve CD represents the variation in the vapour pressure of the solution.

(4) This elevation in the boiling point is proportional to the lowering of the vapour pressure, i.e., P₀ – P, where P₀ and P are the vapour pressures of the pure solvent and the solution.
[ΔT_b ∝ (P₀ – P) or ΔT_b ∝ ΔP]

Question ii.
What are isotonic and hypertonic solutions?
Answer:
(1) Isotonic solutions : The solutions having the same osmotic pressure at a given temperature are called isotonic solutions.

Explanation : If two solutions of substances A and B contain n_A and n_B moles dissolved in volume V (in dm³) of the solutions, then their concentrations are,
C_A = \(\frac{n_{\mathrm{A}}}{V}\) (in mol dm^-3) and
C_B = \(\frac{n_{\mathrm{B}}}{V}\) (in mol dm^-3)

If the absolute temperature of both the solutions is T, then by the van’t Hoff equation,
π_A = C_ART and π_B = C_BRT, where π_A and π_B are their osmotic pressures.
For the isotonic solutions,
π_A = π_B
∴ C_A = C_B
∴ \(\frac{n_{\mathrm{A}}}{V}=\frac{n_{\mathrm{B}}}{V}\)
∴ n_A = n_B
Hence, equal volumes of the isotonic solutions at the same temperature will contain equal number of moles (hence, equal number of molecules) of the substances.

(2) Hypertonic solutions : When two solutions have different osmotic pressures, then the solution having higher osmotic pressure is said to be a hypertonic solution with respect to the other solution.

Explanation : Consider two solutions of substances A and B having osmotic pressures π_A and π_B. If π_B is greater than π_A, then the solution B is a hypertonic solution with respect to the solution A.
Hence, if C_A and C_B are their concentrations, then C_B > C_A. Hence, for equal volume of the solutions, n_B > n_A.

Question iii.
A solvent and its solution containing a nonvolatile solute are separated by a semipermable membrane. Does the flow of solvent occur in both directions? Comment giving reason.
Answer:

1. When a solvent and a solution containing a non-volatile solute are separated by a semipermeable membrane, there arises a flow of solvent molecules from solvent to solution as well as from solution to solvent.
2. Due to higher vapour pressure of solvent than solution, the rate of flow of solvent molecules from solvent to solution is higher.
3. As more and more solvent passes into solution due to osmosis, the solvent content increases, and the rate of backward flow increases.
4. At a certain stage an equilibrium is reached where both the opposing rates become equal attaining an equilibrium.

Question iv.
The osmotic pressure of CaCl₂ and urea solutions of the same concentration at the same temperature are respectively 0.605 atm and 0.245 atm. Calculate van’t Hoff factor for CaCl₂.
Answer:
Given : π_Cacl2 = 0.605 atm;
π_Urea = 0.245 atm
For urea solution, van’t Hoff factor, i = 1
π_Cacl2 = i × (CRT)_Cacl2
π_Urea = (CRT)_Urea

van’t Hoff factor = i = 2.47

Question v.
Explain reverse osmosis.
Answer:
Reverse osmosis : The phenomenon of the passage of solvent like water under high pressure from the concentrated aqueous solution like seawater into pure water through a semipermeable membrane is called reverse osmosis.

The osmotic pressure of seawater is about 30 atmospheres. Hence when pressure more than 30 atmospheres is applied on the solution side, regular osmosis stops and reverse osmosis starts. Hence pure water from seawater enters the other side of pure water.

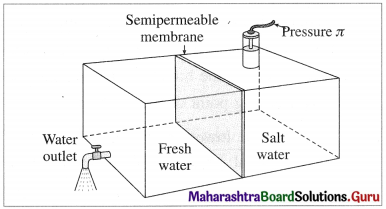
Purification of seawater by reverse osmosis

For this purpose of suitable semipermeable membrane is required which can withstand high pressure conditions over a long period.
This method is used successfully in Florida since 1981 producing more than 10 million litres of pure water per day.

Question vi.
How molar mass of a solute is determined by osmotic pressure measurement?
Answer:
Consider V dm³ (litres) of a solution containing W₂ mass of a solute of molar mass M₂ at a temperature T.
Number of moles of solute, n₂ = \(\frac{W_{2}}{M_{2}}\)
The osmotic pressure π is given by,
π = \(\frac{W_{2} R T}{M_{2} V}\)
∴ M₂ = \(\frac{W_{2} R T}{\pi V}\)
By measuring osmotic pressure of a solution, the molar mass of a solute can be calculated.
Since osmotic pressure can be measured more precisely, it is widely used to measure molar masses of the substances.

Question vii.
Why vapour pressure of a solvent is lowered by dissolving a nonvolatile solute into it?
Answer:
Lowering of vapour pressure of a solution :
When a nonvolatile solute is added to a pure solvent, the surface area is covered by the solute molecule decreasing the rate of evaporation, hence its vapour pressure decreases. This decrease in vapour pressure is called lowering of vapour pressure.

If P₀ is the vapour pressure of a pure solvent (liquid) and P is the vapour pressure of the solution, where P < P₀, then, (P₀ – P) is the lowering of the vapour pressure.

Question viii.
Using Raoult’s law, how will you show that ∆P = \(\boldsymbol{P}_{1}^{0}\)x₂ ? Where x₂ is the mole fraction of solute in the solution and \(\boldsymbol{P}_{1}^{0}\) vapour pressure of pure solvent.
Answer:
If x₁ and x₂ are the mole fractions of solvent and solute respectively, then
x₁ + x₂
By Raoult’s law,
P = x₁ × P₀
where P⁰ is the vapour pressure of a pure solvent and P is the vapour pressure of the solution at given temperature.

Question ix.
While considering boiling point elevation and freezing point depression a solution concentration is expressed in molality and not in molarity. Why?
Answer:

• Boiling point elevation and freezing point depression involve temperature changes, (ΔT_b and ΔT_f).
• Since molarity depends on temperature but molality is independent of temperature we use molality and not molarity in considering boiling point elevation and freezing point depression.

Question 4.
Derive the relationship between degree of dissociation of an electrolyte and van’t Hoff factor.
Answer:
Consider 1 dm³ of a solution containing m moles of an electrolyte AxBy. The electrolyte on dissociation gives number of A^y+ ions and y number of B^x- ions. Let α be the degree of dissociation.

At equilibrium,
AxBy ⇌ xA^y+ + yB^x-
For 1 mole of electrolyte : 1 – α, xα, yα and
For ‘m’ moles of an electrolyte : m(1 – α), mxα, myα are the number of particles.
Total number of moles at equilibrium, will be,
Total moles = m(1 – α) + mxα + myα
= m[(1 – α) + xα + yα]
= m[1 – xα + yα – α]
= m[1 + α(x + y – 1)]
The van’t Hoff factor i will be,

If total number of ions from one mole of electrolyte is denoted by n, then (x + y) = n
∴ i = 1 + α(n – 1)
∴ α(n – 1) = i – 1
∴ α = \(\frac{i-1}{n-1}\) ……..(1)
This is a relation between van’t Hoff factor i and degree of dissociation of an electrolyte.

Question 5.
What is effect of temperature on solubility of solids in water? Give examples.
Answer:
The solubility of a solid solute depends upon temperature.

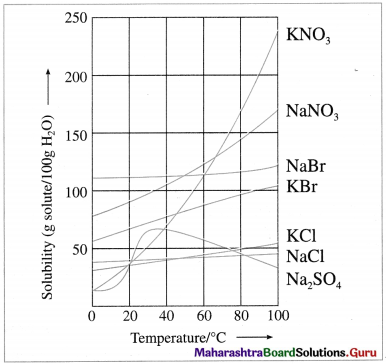
Variation of solubilities of some ionic solids with temperature

• Generally rise in temperature increases the solubility. This is due to expansion of holes or empty spaces in the liquid solvent. Generally 10 °C rise in temperature, increases the solubility of solids two fold.
• Dissolution process may be endothermic or exothermic.
• The solubility of the substances like NaBr, NaCl, KCl, etc. changes slightly with the increase in temperature.
• The solubility of the salts like NaNO₃, KNO₃, KBr, etc. increases appreciably with the increase in temperature.
• The solubility of Na₂SO₄ first increases and after 30 °C decreases with the increase in temperature.

This variation in solubility with temperature can be used to separate the salts from the mixture by fractional crystallisation.

Question 6.
Obtain the relationship between freezing point depression of a solution containing nonvolatile nonelectrolyte and its molar mass.
Answer:
The freezing point depression, ΔT_f of a solution is directly proportional to molality (m) of the solution.
∴ ΔT_f ∝ m
∴ ΔT_f = K_f m
where Kf is a molal depression constant.
The molality of a solution is given by,

If W₁ grams of a solvent contain W₂ grams of a solute of the molar mass M₂, then the molality m of the solution is given by,

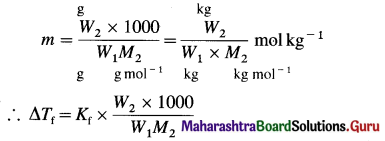
If the weights are expressed in kg then,
ΔT_f = K_f × \(\frac{W_{2}}{W_{1} M_{2}}\)
The unit of K_f is K kg mol^-1
Hence, from the measurement of the depression in the freezing point of the solution, the molar mass of the substance can be determined.

Question 7.
Explain with diagram the boiling point elevation in terms of vapour pressure lowering.
Answer:
(1) The boiling point of a liquid is the temperature at which the vapour pressure of the liquid becomes equal to the external pressure, generally 1 atm (101.3 × 10³ Nm^-2).

(2) When a liquid is heated, its vapour pressure rises till it becomes equal to the external pressure.
If the liquid has a low vapour pressure, it has a higher boiling point.

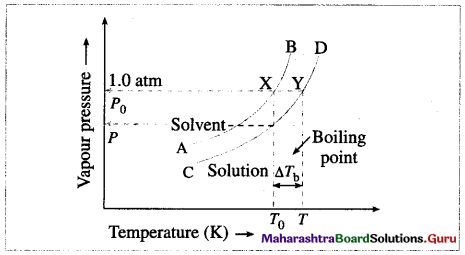
Vapour pressure curve showing elevation in boiling point

(3) When a nonvolatile solute is added to a solvent, its vapour pressure decreases, hence the boiling point increases.
This is explained by graphical representation of the vapour pressure and the boiling point of the pure solvent and the solution.

If T₀ and T are the boiling points of a pure solvent and a solution, then the elevation in the boiling point is given by,
ΔT_b = T – T₀
The curve AB, represents the variation in the vapour pressure of a pure solvent with temperature while curve CD represents the variation in the vapour pressure of the solution.

(4) This elevation in the boiling point is proportional to the lowering of the vapour pressure, i.e., P₀ – P, where P₀ and P are the vapour pressures of the pure solvent and the solution.
[ΔT_b ∝ (P₀ – P) or ΔT_b ∝ ΔP]

Question 8.
Fish generally needs O₂ concentration in water at least 3.8 mg/L for survival. What partial pressure of O₂ above the water is needed for the survival of fish? Given the solubility of O₂ in water at 0 °C and 1 atm partial pressure is 2.2 × 10^-3 mol/L (0.054 atm)
Answer:
Given : Required concentration of O₂
= 3.8 mg/L
= \(\frac{3.8 \times 10^{-3}}{32} \mathrm{~mol} \mathrm{~L}^{-1}\)
Solubility of O₂ = 2.2 × 10^-3 mol L^-1
P = 1 atm
Partial pressure of O₂ needed = Po₂ = ?

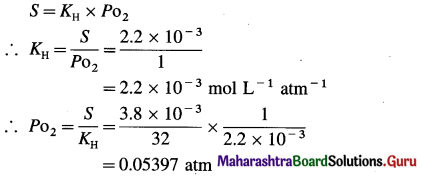
Pressure needed = Po₂ = 0.05397 atm.

Question 9.
The vapour pressure of water at 20 °C is 17 mm Hg. What is the vapour pressure of solution containing 2.8 g urea in 50 g of water? (16.17 mm Hg)
Answer:
Given : Vapour pressure of pure solvent (water) = P0
= 17 mm Hg
Weight of solvent = W₁ = 50 g
Weight of solute (urea) = 2.8 g
Molecular weight of a solvent = M₁ = 18
Molecular weight of a solute (urea) = M₂
= 60 g mol^-1
\(\frac{P_{0}-P}{P_{0}}=\frac{W_{2} \times M_{1}}{W_{1} \times M_{2}}\)
∴ \(\frac{17-P}{17}=\frac{2.8 \times 18}{50 \times 60}\) = 0.0168
∴ 17 – P = 17 × 0.0168
17 – P = 0.2856
∴ P= 17 – 0.2856
= 16.7144 mm Hg
Vapour pressure of solution = 16.7144 mm Hg

Question 10.
A 5% aqueous solution (by mass) of cane sugar (molar mass 342 g/mol) has freezing point of 271K. Calculate the freezing point of 5% aqueous glucose solution.
Answer:
Given : W₂ = 5 g cane sugar; W₁ = 100 – 5 = 95 g
M₂ = 342 g mol^-1; T_f1 = 271 K;
ΔT_f1 = 273 – 271 = 2 K; T_f = ?
W₂ = 5 g glucose, W’₁ = 100 – 5 = 95 g,
M’₂ = 180 g mol-1, ΔT_f2 = ?

= 12.996 K kg mol^-1
≅ 13 K kg mol^-1

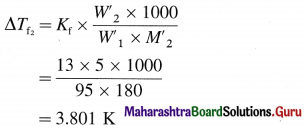
∴ Freezing point of solution = T_f
= 273 – 3.801 = 269.2 K
Freezing point of solution = 269.2 K.

Question 11.
A solution of citric acid C₆H₈O₇ in 50 g of acetic acid has a boiling point elevation of 1.76 K. If K_b for acetic acid is 3.07 K kg mol^-1, what is the molality of solution?
Answer:
Given : W₁ = 50 g acetic acid
ΔT_b = 1.76 K
K_b = 3.07 K kg mol^-1
m = ?
ΔT_b = K_b × m
∴ m = \(\frac{\Delta T_{\mathrm{b}}}{K_{\mathrm{b}}}\)
= \(\frac{1.76}{3.07}\)
= 0.5733 m
Molality of solution = 0.5733 m

Question 12.
An aqueous solution of a certain organic compound has a density of 1.063 gmL^-1, an osmotic pressure of 12.16 atm at 25°C and a freezing point of -1.03°C. What is the molar mass of the compound? (334 g/mol)

Question 13.
A mixture of benzene and toluene contains 30% by mass of toluene. At 30°C, vapour pressure of pure toluene is 36.7 mm Hg and that of pure benzene is 118.2 mm Hg. Assuming that the two liquids form ideal solutions, calculate the total pressure and partial pressure of each constituent above the solution at 30°C.
Answer:
Given : 30% by mass of toluene (T) and 70% by mass of benzene (B).
W_T = 30 g; W_B = 70g
\(P_{\mathrm{T}}^{0}\) = 36.7 mm Hg; \(P_{\mathrm{B}}^{0}\) = 118.2 mm Hg
M_T = 92 g mol^-1; MB = 78 g mol^-1
P_T = ?, P_B = ?, P_soln = ?

Total number of moles = n_Total = n_T + n_B
= 0.326 + 0.8974
= 1.2234 mol

Mole fractions :
x_T = \(\frac{n_{\mathrm{T}}}{n_{\text {Total }}}=\frac{0.326}{1.2234}\) = 0.2665
x_B = 1 – 0.2665 = 0.7335
Psoln = x_T + \(P_{\mathrm{T}}^{0}\) + x_B × \(P_{\mathrm{B}}^{0}\)
= 0.2665 × 36.7 + 0.7335 × 118.2
= 9.780 + 86.7
= 96.48 mm Hg

Partial pressures :
P_T = x_T × P_soln
= 0.2665 × 96.48
= 25.71 mm Hg
P_B = x_B × P_soln
= 0.7335 × 96.48
= 70.77 mm Hg
Total pressure P_soln = 96.48 mm Hg
Partial pressures : P_Toluene = 25.71 mm Hg
P_Benzene = 70.77 mm Hg

Question 14.
At 25 °C a 0.1 molal solution of CH₃COOH is 1.35% dissociated in an aqueous solution. Calculate freezing point and osmotic pressure of the solution assuming molality and molarity to be identical.
Answer:
Given : T = 273 + 25 = 298 K
C = 0.1 m ≅ 0.1 M; K_f = 1.86 K kg mol^-1
Per cent dissociation = 1.35
Freezing point = t_f = ?
π = ?
α = \(\frac{1.35}{100}\) = 0.0135

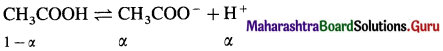
i = 1 – α + α + α = 1 + α = 1 + 0.0135 = 1.0135
(i) ΔT_f = i × K_f × m
= 1.0135 × 1.86 × 0.1
= 0.1885 °C
∴ Freezing point of solution = 0 – 0.1885
= – 0.1885 °C

(ii) n = iCRT
= 1.035 × 0.1 × 0.08206 × 298
= 2.53 atm

(i) Freezing point of solution = – 0.1885 °C
(ii) Osmotic pressure = π = 2.53 atm

Question 15.
A 0.15 m aqueous solution of KCl freezes at -0.510 °C. Calculate i and osmotic pressure at 0 °C. Assume volume of solution equal to that of water.
Answer:
Given : c = 0.15 m KCl ≅ 0.15 M KCl
ΔT_f = 0 – T_f = 0 – (-0.510) = 0.510 °C
T = 273 K; K_f = 1.86 K kg mol^-1
i = ?; π = ?
ΔT_f = i × K_f × m
∴ i = \(\frac{\Delta T_{\mathrm{f}}}{K_{\mathrm{f}} \times m}\)
= \(\frac{0.510}{1.86 \times 0.15}\)
= 1.828
π = iCRT
= 1.828 × 0.15 × 0.08206 × 273
= 6.143 atm
i = 1.828, Osmotic pressure = π = 6.143 atm

12th Chemistry Digest Chapter 2 Solutions Intext Questions and Answers

Can you tell ? (Textbook Page No. 29)

Question 1.
Why naphthalene dissolves in benzene but not in water ?
Answer:
Since naphthalene is a covalent nonpolar substance, it is soluble in a nonpolar solvent like benzene but insoluble in polar solvent like water.

Question 2.
Anhydrous sodium sulphate dissolves in water with the evolution of heat. What is the effect of temperature on its solubility ?
Answer:
Since the dissolution of anhydrous sodium sulphate in water is an exothermic process due to evolution of heat, according to Le Chatelier’s principle its solubility decreases with the increase in temperature.

(Textbook Page No. 42)

Question 1.
If 1.25 m sucrose solution has ΔT_f of 2.32 °C, what will be the expected value of ΔT_f for 1.25 m CaCl₂ solution?
Answer:
Sucrose being nonelectrolyte, it has i = 1 but for CaCl₂,
(CaCl₂ → Ca²⁺ + 2Cl^–) the value of i = 3.
Hence
ΔT_f = i × 2.32
= 3 × 2.32
= 6.92 °C
∴ ΔT_f = 6.92 °C.

(Textbook Page No. 44)

Question 1.
Which of the following solutions will have maximum boiling point elevation and which have minimum freezing point depression assuming the complete dissociation? (a) 0.1m KCl (b) 0.05 m NaCl (c) 1 m AlPO₄ (d) 0.1 m MgSO₄.
Solution :
Boiling point elevation and freezing point depression are colligative properties that depend on number of particles in solution. The solution having more number of particles will have large boiling point elevation and that having less number of particles would show minimum freezing point depression.

AlPO₄ solution contains highest moles and hence highest number particles and in turn, the maximum ΔT_b. NaCl solution has minimum moles and particles, it has minimum ΔT_f.

Question 2.
Arrange the following solutions in order of increasing osmotic pressure. Assume complete ionization. (a) 0.5 m Li₂SO₄ (b) 0.5 m KCl (c) 0.5 m Al₂(SO₄)₃ (d) 0.1 m BaCl₂.
Answer:
Consider 1 dm³ of each solution.

Osmotic pressure being a colligative property, it depends on number of particles in the solution.
Therefore, increasing order of osmotic pressure is,