Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 23 Textbook Exercise Important Questions and Answers.
Maharashtra State Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 23
Question 1.
What is \(\frac{1}{3}\) of each of the collections given below?
(1) 15 pencils
(2) 21 balloons
(3) 9 children
(4) 18 books
Answer:
(1) 15 pencils → \(\frac{1}{3}\) of 15 = 5, 15 ÷ 3 = 5 pencils.
(2) 21 baloons → \(\frac{1}{3}\) of 21 = 7,21 ÷ 3 = 7 baloons.
(3) 9 children → \(\frac{1}{3}\) of 9 = 3, 9 ÷ 3 = 3 chi1dren.
(4) 18 books → \(\frac{1}{3}\) of 18 = 6, 18 ÷ 3 = 6 books.
![]()
Question 2.
What is \(\frac{1}{5}\) of each of the following?
(1) 20 rupees
(2) 30 km
(3) 15 litres
(4) 25 cm
Answer:
(1) 20 rupees → \(\frac{1}{5}\) of 20 = 4, 20 ÷ 5 = 4 rupees.
(2) 30 km → \(\frac{1}{5}\) of 30 = 6, 30 ÷ 5 = 6km.
(3) 15 litres → \(\frac{1}{5}\) of 15 = 3, 15 ÷ 5 = 3 litres.
(4) 25 cm → \(\frac{1}{5}\) of 25 = 5, 25 ÷ 5 = 5cm.
Question 3.
Find the part of each of the following numbers equal to the given fraction.
(1) \(\frac{2}{3}\) of 30
Solution:
\(\frac{2}{3}\) x 30 So, we take \(\frac{1}{3}\) of 30, twice
\(\frac{1}{3}\) x 30 = 10, twice of 10 is 2 x 10 = 20
It means that \(\frac{2}{3}\) x 30 = 20
(2) \(\frac{7}{11}\) of 22
Solution:
\(\frac{7}{11}\) x 22 So, we take of 22, 7 times
\(\frac{1}{11}\) x 22 = 2, seven times of 2 is 2 x 7 = 14
![]()
(3) \(\frac{3}{8}\) of 64
Solution:
\(\frac{3}{8}\) x 64 So, we take \(\frac{1}{8}\) of 64, thrice
\(\frac{1}{8}\) x 64 = 8, 3 times 8 is 3 x 8 = 24
(4) \(\frac{5}{13}\) of 65
Solution:
\(\frac{5}{13}\) x 65 So, we take \(\frac{1}{13}\) of 65, 5 times
\(\frac{1}{13}\) x 65 = 55 times of 5 is 5 x 5 = 25
Mixed fractions
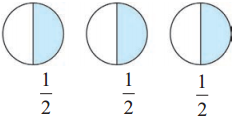
Half of each of the three circles is coloured. That is, 3 parts, each equal to \(\frac{1}{2}\) of the circle, are coloured.
The coloured part is \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\), that is, \(\frac{3}{2}\) or 1 + \(\frac{1}{2}\).
1 + \(\frac{1}{2}\) is written as 1 \(\frac{1}{2}\). 1 \(\frac{1}{2}\) is read as ‘one and one upon two’.
In the fraction 1 \(\frac{1}{2}\), 1 is the integer part and \(\frac{1}{2}\) is the fraction part. Hence, such fractions are called mixed fractions or mixed numbers. 2 \(\frac{1}{4}\), 3 \(\frac{2}{5}\), 7 \(\frac{4}{9}\) are all mixed fractions.
![]()
Fractions in which the numerator is greater than the denominator are called improper fractions.
\(\frac{3}{2}\), \(\frac{5}{3}\) are improper fractions. We can convert improper fractions into mixed fractions.
For example, ![]()
Activities
1. Colour the Hats.

In the picture alongside :
Colour \(\frac{1}{3}\) of the hats red.
Colour \(\frac{3}{5}\) of the hats blue.
How many hats have you coloured red?
How many hats have you coloured blue?
How many are still not coloured?
![]()
2. Make a Magic Spinner.
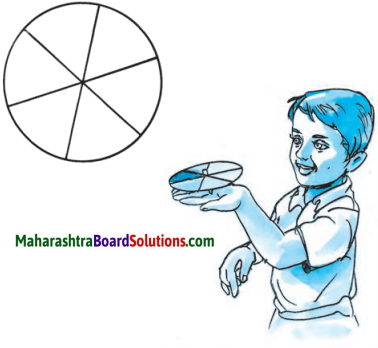
Take a white cardboard disc. As shown in the figure, divide it into six equal parts.
Colour the parts red, orange, yellow, green, blue and violet.
Make a small hole at the centre of the disc and fix a pointed stick in the hole.
Your magic spinner is ready.
What fraction of the disc is each of the coloured parts?
Give the disc a strong tug to make it turn fast. What colour does it appear to be now?
The Clever Poet

![]()
There was a king who had a great love for literature. A certain poet knew that if the king read a good poem it made him very happy. Then the king would give the poet an award. Once, the poet composed a good poem. He thought if he showed it to the king, he would win a prize. So, he went to the king’s palace. But, it was not easy to meet the king. You had to pass a number of gates and guards. The first guard asked the poet why he wanted to meet the king. So, the poet told him the reason. Seeing the chance of getting a share of the award, the guard demanded, ‘You must
give me \(\frac{1}{10}\) of your prize. Only then will I let you go in.’ The poet could do nothing but agree. The second guard stopped him and said, ‘I will let you go in only if you promise me \(\frac{2}{5}\) of your prize.’ The third guard, too, was a greedy man. He said, ‘I will not let you go, unless you promise me \(\frac{1}{4}\) of your prize.’ The king’s palace was just a little distance away. Now, the poet told the guard, ‘Why only \(\frac{1}{4}\), I shall give you half the prize!’ The guard was pleased and let him in.
The king liked the poem. He asked the poet, ‘What is the prize you want?’ ‘I shall be happy if Your Majesty awards me 100 lashes of the whip.’ The king was surprised. ‘Are you out of your mind!’ he exclaimed. ‘I have never met anyone so crazy as to ask for a whipping !’
‘Your Majesty, if you wish to know the reason, the three palace guards must be called here.’ When the guards came, the poet explained, ‘Your Majesty, all of them have a share in the 100 lashes that you have awarded to me. Each of them has fixed his own share of the prize I get. The first guard
![]()
must get \(\frac{1}{10}\) of the award, that is, [ ] lashes. The second must get \(\frac{2}{5}\), which is [ ], and the third must get half the award, that is, [ ] lashes !’ The king could now see how greedy the guards were and how clever the poet was. He saw to it that each guard got the punishment he deserved. He gave the poet a prize for his poem. He also gave him an extra 100 gold coins for exposing the greed of the guards.
What was the clever idea of the poet which the king appreciated so much?
Fractions Problem Set 23 Additional Important Questions and Answers
Question 1.
What is \(\frac{1}{3}\) of each of the collections given below?
(1) 24 marbles →
(2) 6 erasers →
Answer:
(1) 24 marbles → \(\frac{1}{3}\) of 24 = 8, 24 ÷ 3 = 8 marbles.
(1) 6 erasers → \(\frac{1}{3}\) of 6 = 2, 6 ÷ 3 = 2 erasers.
Question 2.
What is \(\frac{1}{5}\) of each of the following?
(1) 35 gm →
(2) 40m →
Answer:
(1) 35 gm → \(\frac{1}{5}\) of 35 = 7, 35 ÷ 5 = 7 gm.
(2) 40m → \(\frac{1}{5}\) of 40 = 8, 40 ÷ 5 = 8m.
![]()
Question 3.
Find the part of each of the following numbers equal to the given fraction:
(1) \(\frac{7}{9}\) of 45
Solution:
\(\frac{7}{9}\) x 45 So, we take \(\frac{1}{9}\) of 45, 7 times
\(\frac{1}{9}\) x 45 = 5, 7 times of 5 is 7 x 5 = 35
(2) \(\frac{3}{7}\) of 28
Solution:
\(\frac{3}{7}\) x 28 So, we take \(\frac{1}{7}\) of 28, thrice
\(\frac{1}{7}\) x 28 = 4, 3 times of 4 is 4 x 3 = 12
Question 4.
Find the proper number in the box:
![]()
![]()
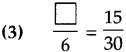
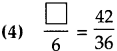
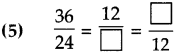
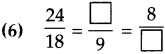
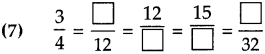
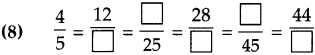
Answer:
(1) 3
(2) 36
(3) 3
(4) 7
(5) 8, 18
(6) 12, 6
(7) 9, 16, 20, 24
(8) 15, 20, 35, 36, 55
![]()
Question 5.
Find an equivalent fraction with denominator 3, for each of the following fractions.
![]()
Answer:
![]()
Question 6.
Find an equivalent fraction with numerator 30 for each of the following fractions.
![]()
Answer:
![]()
Question 7.
Find two equivalent fractions for each of the following fraction.
\(\text { (1) } \frac{5}{7}\)
\(\text { (2) } \frac{8}{9}\)
\(\text { (3) } \frac{7}{13}\)
Answer:
(1) ![]()
(2) ![]()
(3) ![]()
![]()
Question 8.
Match the columns (A) and (B) for having equivalent fractions:
| (A) | (B) | |
| (1) | \(\frac{3}{4}\) | (a) \(\frac{15}{27}\) |
| (2) | \(\frac{5}{9}\) | (b) \(\frac{2}{3}\) |
| (3) | \(\frac{7}{11}\) | (c) \(\frac{27}{36}\) |
| (4) | \(\frac{8}{12}\) | (d) \(\frac{28}{44}\) |
Answer:
(1) ↔ (c)
(2) ↔ (a)
(3) ↔ (d)
(4) ↔ (b)
Question 9.
Convert the given fractions into like fractions:
\(\text { (1) } \frac{1}{10}, \frac{2}{3}\)
\(\text { (2) } \frac{3}{7}, \frac{4}{5}\)
\(\text { (3) } \frac{1}{3}, \frac{3}{5}\)
\(\text { (3) } \frac{1}{4}, \frac{2}{5}\)
Answer:
\(\text { (1) } \frac{3}{30}, \frac{20}{30}\)
\(\text { (2) } \frac{15}{35}, \frac{28}{35}\)
\(\text { (3) } \frac{5}{15}, \frac{9}{15}\)
\(\text { (3) } \frac{5}{20}, \frac{8}{20}\)
![]()
Question 10.
Write the proper symbol from <, > or = in the box:
![]()
![]()
![]()
![]()
![]()
Answer:
(1) >
(2) >
(3) >
(4) >
(5) >
Question 11.
Add the following:
\(\text { (1) } \frac{1}{6}+\frac{2}{6}\)
\(\text { (2) } \frac{1}{4}+\frac{3}{4}\)
\(\text { (3) } \frac{5}{13}+\frac{2}{13}+\frac{3}{13}\)
\(\text { (4) } \frac{2}{9}+\frac{3}{7}\)
\(\text { (5) } \frac{3}{11}+\frac{2}{3}\)
\(\text { (6) } \frac{1}{10}+\frac{4}{5}\)
Answer:
\(\text { (1) } \frac{3}{6}\)
\(\text { (2) } \frac{4}{4}\)
\(\text { (3) } \frac{10}{13}\)
\(\text { (4) } \frac{41}{63}\)
\(\text { (5) } \frac{31}{33}\)
\(\text { (6) } \frac{9}{10}\)
![]()
Question 12.
Subtract the following:
\(\text { (1) } \frac{5}{6}-\frac{1}{6}\)
\(\text { (2) } \frac{3}{5}-\frac{2}{5}\)
\(\text { (3) } \frac{7}{16}-\frac{3}{16}-\frac{1}{16}\)
\(\text { (4) } \frac{5}{6}-\frac{7}{12}\)
\(\text { (5) } \frac{13}{16}-\frac{5}{8}\)
\(\text { (6) } \frac{4}{9}-\frac{3}{10}\)
Answer:
\(\text { (1) } \frac{4}{6}\)
\(\text { (2) } \frac{1}{5}\)
\(\text { (3) } \frac{3}{16}\)
\(\text { (4) } \frac{3}{12}\)
\(\text { (5) } \frac{3}{13}\)
\(\text { (6) } \frac{13}{90}\)
Question 13.
What is \(\frac{1}{4}\) of each of the collections given below:
(1) 20 marbles
(2) 12 pens
(3) 24 notebooks
(4) 8 ladoos
Answer:
(1) 5 marbles
(2) 3 pens
(3) 6 notebooks
(4) 2 ladoos
![]()
Question 14.
What is \(\frac{1}{6}\) of each of the following:
(1) 18 bananas
(2) 12 gms
(3) 30 metres
(4) 24 ₹
Answer:
(1) 3 bananas
(2) 2 gms
(3) 5 metres
(4) 4 ₹
Question 15.
Find the part of each of the following numbers equal to the given fraction.
(1) \(\frac{2}{5}\) of 25
(2) \(\frac{3}{7}\) of 21
(3) \(\frac{4}{9}\) of 36
(4) \(\frac{4}{17}\) of 34
Answer:
(1) 10
(2) 9
(3) 16
(4) 8
![]()
Question 16.
Printed price of. the book was 80. Vikram purchased the book by paying of the printed price of the book. How much he paid for the book?
Answer:
64 ₹