Balbharti Maharashtra State Board Class 8 Science Solutions Chapter 14 Measurement and Effects of Heat Notes, Textbook Exercise Important Questions and Answers.
Maharashtra State Board Class 8 Science Solutions Chapter 14 Measurement and Effects of Heat
Class 8 Science Chapter 14 Measurement and Effects of Heat Textbook Questions and Answers
1. A. Whom should I pair with?
Question a.
| Group ‘A’ | Group ‘B’ | |
| 1. Temperature of a healthy human body | a. 296 K | |
| 2. Boiling point of water | b. 98.6 °F | |
| 3. Room temperature | c. 0°C | |
| 4. Freezing point of water | d. 212 °F | |
Answer:
| Group ‘A’ | Group ‘B’ | |
| 1. Temperature of a healthy human body | b. 98.6 °F | |
| 2. Boiling point of water | d. 212 °F | |
| 3. Room temperature | a. 296 K | |
| 4. Freezing point of water | c. 0°C | |
![]()
B. Who is telling the truth?
Question a.
The temperature of a substance is measured in joule.
Answer:
False. (The temperature of a substance is measured in °C or °F or K.)
Question b.
Heat flows from an object at higher temperature to an object at lower temperature.
Answer:
True.
Question c.
The joule is the unit of heat.
Answer:
True.
Question d.
Objects contract on heating.
Answer:
False. (In general, objects expand on heating. There are some exceptions to this, you will learn about them in Standard X.)
![]()
Question e.
Atoms of a solid are free.
Answer:
False. (Atoms of a solid are bound to each other due to the forces acting between them.)
Question f.
The average kinetic energy of atoms in a hot object is less than the average kinetic energy of atoms in a cold object.
Answer:
False. (The average kinetic energy of atoms in a hot object is more than the average kinetic energy of atoms in a cold object.)
C. You will find if you search.
Question a.
A thermometer is used to measure ……………. .
Answer:
A thermometer is used to measure temperature.
Question b.
The apparatus used to measure heat is called a ………… .
Answer:
The apparatus used to measure heat is called a calorimeter.
![]()
Question c.
Temperature is the measure of the …………. kinetic energy of the atoms in a substance.
Answer:
Temperature is the measure of the average kinetic energy of the atoms in a substance.
Question d.
The heat contained in a substance is the measure of the ………….. kinetic energy of the atoms in the substance.
Answer:
The heat contained in a substance is the measure of the total kinetic energy of the atoms in the substance.
2. Nishigandha kept a vessel containing all the ingredients for making tea in a solar cooker. Shivani kept a similar vessel on a stove. Whose tea will be ready first and why?
Question a.
Nishigandha kept a vessel containing all the ingredients for making tea in a solar cooker. Shivani kept a similar vessel on a stove. Whose tea will be ready first and why?
Answer:
Shivani’s tea will be ready first.
Reason: In a given time, the amount of heat received by the vessel on a stove is far greater than that received by the vessel kept in a solar cooker.
![]()
3. Write brief answers.
Question a.
Describe a clinical thermometer. How does it differ from the thermometer used in a laboratory?
Answer:
A clinical thermometer has a narrow stem and a long bulb filled with mercury (or alcohol). There is a small constriction in the stem above the bulb. When the bulb of the thermometer is held in the armpit or the mouth of a patient, the mercury (or alcohol) in the bulb rises in the stem.
When it is taken out of the patient’s body, the small constriction does not allow the mercury (or alcohol) from the stem to retreat into the bulb. Thus, this arrangement enables us to read the temperature of the patient’s body at ease after the removal of the thermometer from his body.
The clinical thermometer is graduated from 35 °C to 42 °C (or from 95 °F to 108 °F). At 37 °C (98.6 °F), there is a red arrow mark which indicates the temperature of a healthy person.
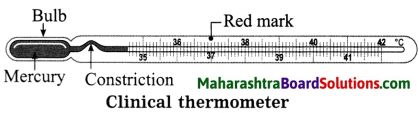
The thermometer used in a laboratory has wider range and does not have constriction like a clinical thermometer.
Question b.
What is the difference between heat and temperature?
Answer:
Heat is related to the total kinetic energy of the atoms in a substance while temperature is related to the average kinetic energy of the atoms in the substance. Heat flows from a body at higher temperature to a body at lower temperature. Thus, temperature is a quantity that determines the direction of flow of heat. It is a quantitative measure of the degree of hotness or coldness of a body.
Higher temperature does not mean higher heat content. Suppose a vessel A contains 2 litres of water at 90 °C and a vessel B contains 100 ml of water at 91 °C. Then the heat content of water in A is greater than that of water in B, but the temperature of water in B is higher than that of water in A.
Units of heat:
Heat is usually expressed in calorie, kilocalorie and joule. It can also be expressed in erg as heat is a form of energy.
![]()
Question c.
Explain the construction of a calorimeter. Draw the necessary figure.
Answer:
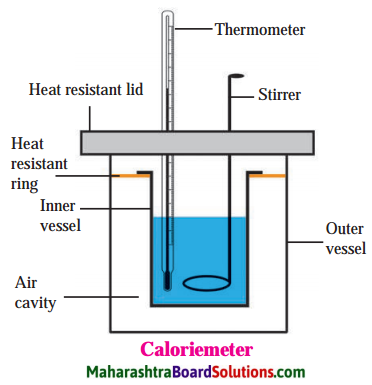
Figure shows the construction of a calorimeter. Like a thermo flask, a calorimeter has two vessels. The inner vessel, made of copper, is (practically) thermally isolated from the surroundings. The outer vessel is made of wood and is covered with a heat resistant lid. The lid has two holes, one for the thermometer and the other for the stirrer. The inner and outer surfaces of the inner vessel are polished for minimizing exchange of heat with the surroundings by radiation. A heat resistant ring covers the inner vessel.
Question d.
Explain why rails have gaps at specific distances.
Answer:
The rails expand in summer due to increase in the temperature of the atmosphere. Also, they expand due to rise in temperature caused by the friction between the rails and the wheels of the running train. If there is no gap between successive rails of a railway line, the rails would bend due to expansion. This bending and twisting of the rails would cause accidents. Hence, a gap is kept between successive rails of a railway line to make provision for their expansion in summer.
Do you know:
Have you seen rails? They are not continuous. A small gap is kept between them at regular intervals. This is shown in the figure. This is kept to accommodate the change in the length of the rails with change in temperature. If this gap is not kept, then the rail will get distorted due to expansion in summer which may lead to accidents.

Similar to rails, the length of bridges can also increase due to expansion in summer. The length of the 18 km long great belt bridge in Denmark increases by 4.7 m in summer. Therefore, provision in made in the construction of the bridges to accommodate this expansion.
![]()
Question e.
Explain with the help of formulae the expansion coefficients of liquid and gas.
Answer:
1. A liquid is held in a container. When it is heated, both the container and the liquid expand. The expansion of the container is usually very small compared to that of the liquid in it. Often, it can be ignored.
Suppose a liquid is heated so that its temperature rises by ΔT (very small) and its volume increases from V1 to V2. Experimentally, it is found that the increase in volume, V2 – V1, is proportional to V1 and ΔT.
Hence, (V2 – V1) α V1ΔT.
∴ V2 – V1 = β V1ΔT, where β is a constant of proportionality called the volumetric expansion coefficient of the liquid.
β = \(\frac{V_{2}-V_{1}}{V_{1} \Delta T}\).
It is expressed in per °C.
We have V2 = V1 + βV1ΔT = V1(1 + β ΔT).
β is the increase in the volume of a liquid per unit original volume per unit rise in its temperature.
2. A gas is enclosed in a container. When it is heated at constant pressure, both the container and the gas expand. Suppose a gas is heated at constant pressure so that its temperature rises by ΔT (very small) and its volume increases from V1 to V2. Experimentally, it is found that the increase in volume, V2 – V1 is proportional to V1 and ΔT. Hence, (V2 – V1) a V1ΔT.
∴ V2 – V1 = β V1ΔT, where β is a constant of proportionality, the volumetric expansion coefficient, called the constant pressure expansion coefficient.
β = \(\frac{V_{2}-V_{1}}{V_{1} \Delta T}\).
It is expressed in per °C.
We have V2 = V1 + βV1T = V1(1 + β ΔT).
β is the increase in the volume of a gas per unit original volume per unit rise in its temperature when the pressure is kept constant.
![]()
4. Solve the following examples.
Question a.
What must be the temperature in Fahrenheit so that it will be twice its value in Celsius?
Solution:
Data: F = 2 C ∴ C = F/2, F = ?

∴ F – 0.9 F = 32
∴ 0.1 F = 32
∴ F = \(\frac{32}{0.1}\) = 320 °F.
Question b.
A bridge is made from 20 m long iron rods. At temperature 18 °C, the distance between two rods is 0.4 cm. Up to what temperature will the bridge be in good shape?
Solution:
Data: l1 = 20 m, l2 – l1 = 0.4 cm
= 4 × 10-3 m, Ti = 18 °C, λ for iron = 11.5 × 10-6/°C
l2 – l1 = λl1 Δt

= \(\frac{400}{23}\) °C = about 17.39 °C
Now, ΔT= Tf – Ti ∴ Tf = Ti + ΔT
∴ Tf = 18 °C + 17.39 °C = 35.39 °C.
The bridge will be in good shape up to 35.39 °C.
Question c.
At 15 °C the height of Eiffel Tower is 324 m. If it is made of iron, what will be the increase in length in cm, at 30 °C?
Solution:
Data: ΔT = 30 °C – 15 °C = 15 °C, l1 = 324 m, λ for iron = 11.5 × 10-6/°C l2 – l1 = λl1 ΔT
= 11.5 × 10-6/°C × 324 m × 15 °C
= 55890 × 10-6 m
= 55890 × 10-6 × 102 cm
= 55890 × 10-4 cm
= 5.589 cm (nearly 5.6 cm)
This is the increase in the length, i.e., the increase in the height of Eiffel Tower.
![]()
Question d.
Two substances A and B have specific heats c and 2 c respectively. If A and B are given Q and 4Q amounts of heat respectively, the change in their temperatures is the same. If the mass of A is m, what is the mass of B?
Solution:
Data: c (A) = c, c (B) = 2c,
Q (A) = Q, Q (B) = 4Q, ΔT same,
m (A) = m, m (B) = ?

∴ m(B) = 2m.
This is the mass of B.
Question e.
When a substance having mass 3 kg receives 600 cal of heat, its temperature increases by 10 °C. What is the specific heat of the substance?
Solution:
Data: m = 3 kg = 3000 g,
Q = 600 cal, ΔT = 10 °C, c = ?
Q = mcΔT
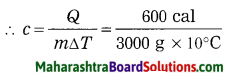
= 0.02 cal/(g.°C)
This is the specific heat of the substance.
Can you recall?
Question a.
Which sources do we get heat from?
Answer:
- Sun
- earth
- fuels like wood, coal, petrol
- electricity
- atomic energy
- air.
![]()
Question b.
How is heat transferred?
Answer:
Heat is transferred by conduction, convection and radiation.
Question c.
Which effects of heat do you know?
Answer:
Expansion, change of state, rise in temperature, emission of light, burning.
Question d.
Some effects of heat are shown in Fig. What are they?

Answer:
Rise in temperature/boiling, melting, burning, expansion.
Question e.
What are potential and kinetic energies?
Answer:
The energy stored in a body because of its specific state or position is called its potential energy. The energy possessed by a body because of its motion is called it’s kinetic energy.
![]()
Project:
Question a.
Collect information about bimetallic strips and discuss in your class how a fire alarm is made using it.
Class 8 Science Chapter 14 Measurement and Effects of Heat Important Questions and Answers
Rewrite the following statements by selecting the correct options:
Question 1.
32°F is equal to …………….. .
(a) 212 °C
(b) 212 K
(c) 273.15 K
(d) 273.15 K
Answer:
32°F is equal to 273.15 K.
Question 2.
-40°C is equal to ………….. .
(a) -40 °F
(b) 40 °F
(c) -8°F
(d) 40K
Answer:
-40°C is equal to -40 °F.
![]()
Question 3.
The boiling point of water is ………… .
(a) 212 K
(b) 212 °F
(c) 273.15 K
(d) 32 °F
Answer:
The boiling point of pure water is 212 °F.
Question 4.
Specific heat is expressed in …………… .
(a) J/(kg. °C)
(b) kg/(J C)
(c) J/kg
(d) cal/g
Answer:
Specific heat is expressed in J/(kg.°C).
Question 5.
The freezing point of water is …………….. .
(a) OK
(b) 212°F
(c) 32°F
(d) 0°F
Answer:
The freezing point of water is 32 °F.
Find the odd one out and give the reason:
Question 1.
0°C, 32°F, 273.15K, 212°F.
Answer:
212 °F. This is the boiling point of water; others correspond to the freezing point of water.
![]()
Question 2.
373.15 K, 100 °C, 212 °F, 32 °F.
Answer:
32 °F. This is the freezing point of water others correspond to the boiling point of water.
Answer the following questions in one sentence each:
Question 1.
Name the biggest source of heat received by the earth.
Answer:
The Sun is the biggest source of heat received by the earth.
Question 2.
What is the relation between the temperature in °C and the temperature in °F?
F – 32 °C
Answer:
\(\frac{F-32}{9}\) = \(\frac{C}{5}\), where C denotes temperature in °C and F denotes temperature in °F.
Question 3.
Name the quantity expressed in cal/(g.°C).
Answer:
Specific heat is expressed in cal/(g.°C).
Question 4.
State the formula for the coefficient of linear expansion of a solid substance.
Answer:
λ = (l2 – l1]) / (l1 ΔT).
Question 5.
State the formula for the coefficient of areal expansion of a solid.
Answer:
σ = (A2 – A1)/ (A1 ΔT).
![]()
Question 6.
State the formula for the volumetric expansion coefficient of a solid.
Answer:
β = (V2 – V1) / (V1 ΔT).
Question 7.
State the relation between λ and σ (if ΔT is very small).
Answer:
σ = 2 λ.
Answer the following questions:
Question 1.
How is heat generated in the Sun?
Answer:
In the interior of the Sun, at the centre, hydrogen nuclei fuse together to form helium nuclei. A lot of heat is generated in this process.
Question 2.
What is geothermal energy?
Answer:
Heat within the interior of the earth, e.g., that coming from the molten core of the earth, is called geothermal energy.
[Note: Volcanoes, geysers, hot springs are sources of this energy.]
![]()
Question 3.
What is atomic energy or nuclear energy?
Answer:
Energy released or obtained in nuclear fission or nuclear fusion is called atomic energy or nuclear energy.
Question 4.
Name three sources of chemical energy.
Answer:
Fuels like wood, coal and petrol are sources of chemical energy.
Try this:
- Take three similar vessels. Let us call them ‘A’, ‘B’ and ‘C’.
- Fill A with hot water and B with cold water. Put some water from A and B in C.
- Dip your right hand in A and left hand in B and keep them immersed for 2 to 3 minutes.
- Now dip both the hands in C. What do you feel?
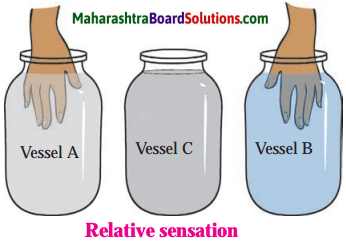
Even though, both the hands are dipped in water in the same vessel, i.e., water at the same temperature, your right hand will find the water to be cold while the left hand will find it to be hot. What is the reason for this? Think about it.
Answer:
The right hand finds the water cold because it loses heat to water in C. The left-hand feels the water hot because it gains heat from water in C. (This shows that we cannot determine the temperature of an object accurately by simply touching it)
![]()
Question 5.
State the units in which temperature is expressed.
OR
What are the units of temperature?
Answer:
Temperature is expressed in °C (degree Celsius), °F (degree Fahrenheit) and K (kelvin).
Question 6.
Draw diagrams to illustrate motion of atoms in a gas and a solid. Also explain the type of motion.
Answer:
Atoms of a gas are comparatively free and move at random. Figures a and b show the velocities of atoms in a gas at high and low temperature, respectively. The direction and the length of the arrows show respectively the direction and the magnitude of the velocity of the atoms. The velocity of atoms in the gas at higher temperature is larger in magnitude than the velocity of atoms in the gas at lower temperature.
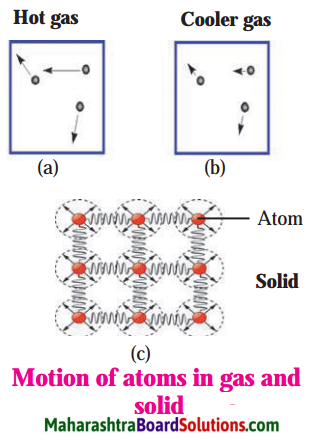
The velocities of atoms in a solid are shown by arrows in Fig. (c). The atoms in a solid are tied to one another because of the forces acting between them. This is indicated by drawing springs between adjacent atoms. Because of heat, they oscillate around their fixed mean positions. The higher the temperature of a solid, the greater is their velocity of oscillation.
![]()
Try this:
1. Take two steel vessels A and B of the same size.
2. Fill some water in A and double that amount in B. Make sure that the water in both vessels is at the same temperature.
3. Raise the temperatures of water in both vessels by 10 CC using a spirit lamp. Did it take the same time to increase the temperature in the two vessels?
Answer:
No.
You must have required more time to raise the temperature of water in B. This means that for the same increase in temperature, you had to give more amount of heat to B. Thus, even though the water in A and in B have the same temperature, the amount of heat in B is more than that in A.
Question 7.
How are the different units of temperature-related?
Answer:
1. The SI unit of temperature is the kelvin (K). Temperature is also expressed in °C (degree Celsius) and °F (degree Fahrenheit).
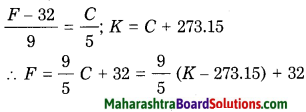
Here, C denotes temperature in °C, F denotes temperature in 0F and K denotes temperature in K (kelvin).
[Notes: (i) The unît degree Celsius is named in honour of Anders Celsius (1701 – 44) Swedish astronomer. He devised a temperature scale in 1742.
(ii) The unit degree Fahrenheit is named in honour of Gabriel Daniel Fahrenheit (1686 – 1736) German physicist. He developed the mercury thermometer and devised the temperature scale.
(iii) The unit kelvin is named in honour of William Thomson, 1st Baron Kelvin (of Largs) (1824 – 1907) British physicist and electrical engineer. He made significant contribution in thermodynamics and electromagnetic theory. He proposed a scale of temperature now known as the Kelvin scale or thermodynamic scale.]
![]()
Question 8.
What is a liquid (mercury or alcohol) thermometer?
Answer:
A thermometer in which the change in the volume of a liquid (mercury or alcohol) with temperature is used for measurement of temperature is called a liquid thermometer.
Question 9.
Why has mecury been replaced by alcohol in a thermometer?
Answer:
Because mercury is harmful for us, it has been replaced by alcohol in a thermometer.
[Notes: (i) Mercury thermometers are still widely used in laboratories in schools and colleges.
(ii) A thermometer is a device to measure temperature. A thermometer containing mercury in its bulb is called a mercury thermometer. There are other types of thermometer such as a thermocouple thermometer, a platinum resistance thermometer, a thermistor thermometer, etc.]
Question 10.
Describe the construction of mercury thermometer.
Answer:
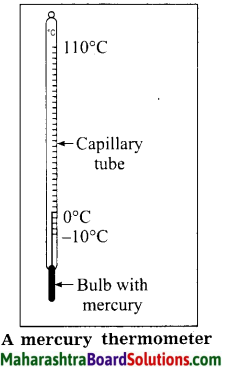
- For constructing a thermometer, a thick-walled capillary tube with a uniform bore is taken. The tube has a thin-walled glass bulb at one end.
- The bulb and a small part of the tube is filled with mercury. The other end of the tube is sealed after removing air from it.
- The tube is then calibrated and the temperature of the substance can be read with it.
[Note: The range of an alcohol thermometer is different from that of a mercury thermometer.]
![]()
Question 11.
How does a mercury thermometer work?
Answer:
1. When the bulb of the thermometer is brought in contact with the substance whose temperature is to be measured, there is an exchange of heat between the substance and the mercury in the bulb.
2. The mercury expands or contracts depending upon whether it gains heat or loses heat. Accordingly there is a rise or fall of the level of mercury in the tube of the thermometer indicating the temperature of the substance when the mercury and the substance are in thermal equilibrium.
Question 12.
Why is the bore of a thermometer made very small?
Answer:
The bore of a thermometer is made very small so that even a slight variation in the temperature may cause noticeable variation in the mercury level in the tube of the thermometer. As a result, the sensitivity of the thermometer increases and even small changes in the temperature can be recorded.
Question 13.
Why does the bulb of a thermometer have a thin glass wall?
Answer:
The bulb of a thermometer is made of a thin glass so that it can easily conduct the heat from the substance in contact with the mercury in the bulb.
Question 14.
Why does a thermometer usually break at the bulb?
Answer:
The bulb of a thermometer has a thin glass wall. Therefore, a thermometer usually breaks at the bulb.
![]()
Question 15.
Explain why the capillary tube of a clinical thermometer has a constriction.
Answer:
When the temperature of a patient is measured with a clinical thermometer, the mercury in the bulb expands and rises in the tube. The small constriction in the thermometer prevents the mercury thread from retreating into the bulb. Thus, the patient’s temperature can be read at ease after removing the thermometer from his body.
Question 16.
Explain why a clinical thermometer should not be washed with hot water.
Answer:
A clinical thermometer is constructed for the purpose of recording the temperature of the human body. Hence, its stem is such that it can allow the mercury to rise up to a temperature of about 42 °C. The temperature of hot water may be more than 42 °C. Therefore, when a clinical thermometer is washed with hot water, mercury will not have enough room for expansion and the thermometer would break.

[Note: (1) A digital thermometer has a sensor that detects the heat coming out from the body directly and displays the temperature.
(2) The maximum-minimum temperature has two scales, one against each arm of the thermometer. One scale indicates the maximum temperature reached (generally during the day) and the other scale indicates the minimum temperature reached (generally during the night).]
![]()
Question 17.
Explain what happens when there is exchange of heat between two objects.
Answer:
When there is an exchange of heat between a hot object and a cold object, the temperature of the hot object falls and the temperature of the cold object rises. If this system of two objects is isolated from the surroundings so that no heat enters or leaves the system, then, heat lost by the hot object = heat gained by the cold object. After some time, the average kinetic energies of the atoms in the two objects become equal, i.e., the two objects attain the same temperature.
Question 18.
Define specific heat.
Answer:
The specific heat of an object (substance) is the amount of heat required to increase the temperature of unit mass of that substance through one degree.
Question 19.
Write the formula for specific heat. Hence, obtain its unit.
Answer:
Specific heat of a substance,
c = \(\frac{Q}{m\left(T_{\mathrm{f}}-T_{\mathrm{i}}\right)}\), where m is the mass of the substance and Q is the amount of heat supplied to the substance to increase its temperature from Ti to Tf.
![]()
The SI unit of heat is the joule (J), that of mass is kg and that of temperature is kelvin (K).
∴ The SI unit of specific heat = \(\frac{\mathrm{J}}{(\mathrm{kg} \cdot \mathrm{K})}\)
[Note: Specific heat is also expressed in J/(kg°C) and cal/(g°C).]
Question 20.
The specific heat of aluminium is 0.21 cal/(g°C). What do you understand by this statement?
Answer:
The amount of heat required to raise the temperature of 1g of aluminium through 1 °C is 0.21 cal.
![]()
Question 21.
The specific heat of gold is 0.03 cal/(g°C). Express it in J/(kg°C).
Answer:
1 cal = 4.18 joules (J)
1 gram = 10-3 kg
∴ 1 cal/(g°C) = 4.18 J/(10-3 kg°C)
= 4180 J/(kg°C)
∴ 0.03 cal/(g°C) = 0.03 × 4180 J/(kg°C)
= 125.4 J/(kg °C)
Question 22.
Arrange the following materials in increasing order of specific heat: aluminium, gold, iron, water.
Answer:
Gold, iron, aluminium, water.
Use your brain power!
Question 1.
Why does your mother put folded cloth strips soaked in cold water on your forehead when you have high fever?
Answer:
To remove heat quickly from our body and thereby lower the temperature of the body (as water has high specific heat).
Question 2.
Why is the calorimeter made of copper?
Answer:
Copper is a good conductor of heat and has low specific heat. Also copper is durable and not highly reactive.
![]()
Question 23.
How will you determine the specific heat of a metal using a calorimeter?
OR
Describe the experiment to determine the specific heat of iron using an iron ball, calorimeter and water.
Answer:
1. Find the mass (mi) of the iron ball.
2. Find the total mass (mc) of the calorimeter (metal container) and the stirrer.
3. Fill the calorimeter to two-thirds of its capacity with water and find its mass (m’c) along with the stirrer. Hence, find the mass (mw) of the water in the calorimeter (mw = m’c – mc).
4. Keep the calorimeter in the wooden box and note the temperature (T1) of the water in the calorimeter with the thermometer.
5. Suspend the iron ball in water in a beaker. Heat the beaker so that the water starts boiling. Note the temperature (T2) of the boiling water.
6. Transfer the iron ball quickly to the calorimeter and cover the calorimeter with the lid immediately.
7. Stir the water in the calorimeter gently and continuously for uniformity of temperature and note the maximum temperature (T3) attained by the mixture.
8. Find the specific heat capacity of iron using the following formula:
heat lost by the iron ball = heat gained by the calorimeter, stirrer and water
[assuming that there is no exchange of heat between the system (calorimeter, stirrer, water and iron ball) and the surroundings].
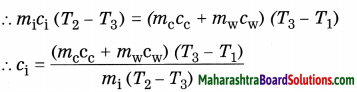
where cc = specific heat of the material of the calorimeter and stirrer and cw = specific heat of water.
Hence, the specific heat of iron (ci) can be determined when other quantities are known.
Question 24.
Why is a calorimeter used in the study of the exchange of heat between a solid and liquid or between two liquids?
Answer:
When a hot body is kept in contact with a cold one, there is an exchange of heat between the two. Hence, the temperature of the hot body decreases while that of the cold body increases till both the bodies attain the same temperature. During this process, if there is no exchange of heat between the surrounding and the bodies, the heat lost by the hot body is equal to the heat gained by the cold body.
As a calorimeter ensures that there is hardly any exchange of heat between the contents of the calorimeter and the surroundings, the calorimeter is used in the study of the exchange of heat between a solid and liquid or between two liquids.
![]()
Question 25.
Explain why the inside and outside of a calorimeter are polished.
Answer:
- A calorimeter is used for the measurement of heat. Hence, it is essential to minimize the exchange of heat between the vessel and the surroundings.
- A polished surface is a good reflector of heat. Hence, by polishing the inside and outside of a calorimeter, the loss or gain of heat due to radiation is reduced to a considerable extent.
Question 26.
Explain with the help of a formula the coefficient of linear expansion of a solid.
Answer:
Suppose a rod of length l1 at temperature T1 is heated to temperature T2 such that ΔT = T2 – T1 is very small. Let l2 be the length of the rod at temperature T2.
Experimentally, it is found that the increase in the length of the rod (linear expension), l2 – l1, is proportional to l1 and ΔT. Therefore, (l2 – l1) α, l1ΔT
∴ l2 – l1 = λl1 ΔT, where X is the constant of proportionality, called the coefficient of linear expansion of the solid.
λ = \(\frac{l_{2}-l_{1}}{l_{1} \Delta T}\) It is expressed in per °C.
We have l2 – l1 + λΔT = l1 (1 + λΔT).
![]()
Question 27.
Define coefficient off linear explansion of a solid. Write the formula for it and obtain its unit.
Answer:
Coefficient of linear expansion of a solid is defined as the increase in the length of a rod of the solid per unit initial length per unit rise in its temperature.
Coefficient of linear expansion of a solid,
λ = \(\frac{l_{2}-l_{1}}{l_{1} \Delta T}\), where l1 and l2 are respectively the initial and final length of the rod of the solid and ΔT is the rise in its temperature.
Unit of λ = \(\frac{\text { unit of length }}{\text { unit of length } \times \text { unit of temperature }}\)
Question 28.
The coefficient of linear expansion of silver is 18 ×10-6 per °C. What do you understand by this statement?
Answer:
If the temperature of a silver rod of length lm is increased by 1 °C, the length of the rod increases by 18 × 10-6 m.
Question 29.
Explain with the help of a formula the coefficient of areal expansion of a solid.
Answer:
Suppose a sheet of a solid with surface area A1 at temperature T1 is heated to temperature T2 such that ΔT = T2 – T1 is very small. Let A2 be the surface area of the sheet at temperature T2. Experimentally, it is found that the increase in the surface area of the sheet (areal expansion), A2 – A1, is proportional to A1 and ΔT. Therefore,
(A2 – A1)α A1 ΔT
∴ A2 – A1 = σ Al1ΔT, where a is the constant of proportionality, called the coefficient of areal expansion of the solid.
σ = \(\frac{A_{2}-A_{1}}{A_{1} \Delta T}\). It is expressed in per °C.
We have A2 = A1 + σA1ΔT = A1 (1 + σΔT).
σ is the increase in the area of a solid per unit original area per unit rise in its temperature.
[Note: Consider a thin square metal plate of length l. Area of one face of the plate = A = l2. Suppose the plate is heated so that the rise in its temperature is ΔT (assumed to be very small). Then in the usual notation, Δl = l λΔT and ΔA =
AσΔT = l2 σΔT. Also, ΔA = (l + Δl)2 – l2 = l2 + 2l.Δl + Δl2 – l2 = 2l.Δl + Δl2 . As Δl2 << 2l.Δl, we can write ΔA = 2l.Δl(approximately)
∴ ΔA = 2l(l λΔT) = 2l2λΔT but ΔA = l2σΔT
∴ σ = 2.λ]
![]()
Question 30.
Explain with the help of a formula the volumetric expansion coefficient of a solid.
Answer:
Suppose a solid with volume V1 at temperature T1 is heated to temperature T2 such that T1 = T2 – T1 is very small. Let V2 be the volume of the solid at temperature T2. Experimentally, it is found that the increase
in the volume of the solid (volumetric expansion), V2 – V1, is proportional to V1 and ΔT. Therefore, (V2 – V1)α V1ΔT.
∴ V2 – V1 = βV1ΔT, where β is the constant of proportionality, called the volumetric expansion coefficient of the solid.
β = \(\frac{V_{2}-V_{1}}{V_{1} \Delta T}\) It is expressed in per °C.
We have V2 = V1 + βV1 ΔT = V1 (1 + βΔT).
is the increase in the volume of a solid per unit original volume per unit rise in its temperature.
[Note: It can be shown that β = \(\frac{3}{2}\) σ 3λ.]
Question 31.
Obtain an expression for the variation of the density of a solid with temperature.
Answer:
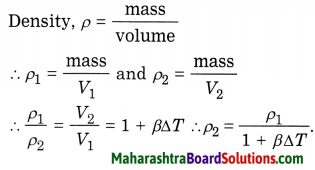
As the temperature increases, density decreases.
Use your brain power!
Question 1.
Which use of the expansion of liquids in daily life do you know?
Answer:
Use of a thermometer. The effect of heat on water is somewhat different from that for other liquids. This is called anomalous behaviour of water. We are going to learn about it in higher standard.
![]()
Can you recall?
Expansion of gases:
A gas does not even have a fixed volume. Gas expands on heating but if the gas is kept in a closed box, its volume cannot increase but its pressure increases. This is shown in Fig. Observe Fig. and find out answers to the questions.
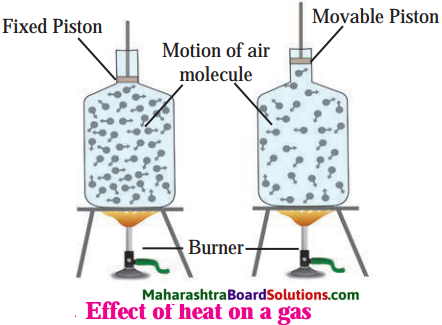
Question 1.
Using the formula density = mass/volume, explain what will be the effect of heat on the gas kept in a closed bottle.
Answer:
The density of the gas will remain the same as there is no change on the mass and volume of the gas.
![]()
Question 2.
If the bottle is not closed but has a movable piston attached to its open end (see the figure), what will be the effect of heating the gas in the bottle?
Answer:
The piston will move upwards as the gas expands.
Therefore, the expansion of a gas is measured by keeping its pressure constant.
Use your brain power!
Question 1.
The density of a gas decreases on heating. Which of the pictures in Fig. makes use of this?
Answer:
Students should be able to answer this question.
Write short notes on the following:
Question 1.
The Celsius temperature scale:
Answer:
In this case, the temperature at which pure ice melts at normal atmospheric pressure is taken as zero degree (0°C) and the temperature at which pure water boils at normal atmospheric pressure is taken as hundred degree (100 °C). The interval between them is divided into loo equal parts. Each part corresponds to a temperature difference of 1 °C.
![]()
Question 2.
The Fahrenheit temperature scale:
Answer:
In this case, the normal melting point of pure ice is taken as 32 °F and the normal boiling point of pure water is taken as 212 °F. The interval between these two points is divided into 180 equal parts. Each part corresponds to a temperature difference of 1°F. If C is the temperature of a body on the Celsius scale and F is the corresponding temperature on the Fahrenheit scale, the two are related by
C = \(\frac{5}{9}\) (F – 32) or F = \(\frac{9}{5}\) C + 32.
Question 3.
The Kelvin temperature scale:
Answer:
In this case, the melting point of pure ice at normal atmospheric pressure is taken as 273.15 kelvin (273.15 K) and the boiling point of pure water at normal f atmospheric pressure is taken as 373.15 I kelvin (373.15 K). The lowest possible temperature (called the absolute zero) on this scale corresponds to -273.15 °C.
Give scientific reasons:
Question 1.
We heat the neck of a glass bottle in order to remove the firmly fitted stopper.
Answer:
When we heat the neck of the glass bottle, it expands. Due to this, the stopper becomes loose and can be removed with ease.
Question 2.
A clinical thermometer has to be jerked before re-use.
Answer:
The constriction above the bulb of the clinical thermometer prevents the mercury thread once risen from falling down to the bulb. Hence, in order to force the mercury thread back into the bulb, the 1 clinical thermometer has to be jerked before re-use.
![]()
Question 3.
Instead of the mercury thermometer, alcohol thermometer is used for measurement of very low temperature.
Answer:
Mercury freezes at – 39 °C and turns to a solid. Hence, the mercury thermometer cannot be used to measure temperature below -39°C. The freezing point of alcohol is -117°C. Hence, the alcohol thermometer is used for i measurement of very low temperature.
Solve the following examples:
Question 1.
The normal armpit temperature in humans is 98.6 °F. What is this temperature in (i) degree Celsius (ii) kelvin ?
Solution:
Data: F = 98.6 °F, C = ?, K = ?
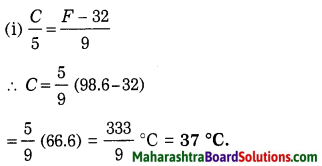
(ii) K = C + 273.15
= 37 + 273.15 = 310.15 K.
Question 2.
Find the heat needed to raise the temperature of 2.5 kg of water from 30 °C to 40 °C. Write the answer in calorie as well as joule.
Solution:
Data: m = 2.5 kg = 2500 g,
ΔT = 40 °C-30 °C, Q = ?
Heat needed to raise the temperature of 1 g of water through 1°C is 1 calorie.
∴ Q = 2500 × 10 = 25000 calories
Now, 1 calorie = 4.18 joules
∴ Q = 25000 × 4.18 joules = 104500 joules
Heat needed, Q = 25000 calories = 104500 joules.
![]()
Question 3.
If the temperature of water rises by 5 °C when 500 cal of heat is supplied to it, what is the mass of water?
Solution:
Mass of water = \(\frac{500}{5}\) = 100 g.
Question 4.
How much heat is required to raise the temperature of 500 g of mercury from 20 °C to 100 °C? [Specific heat of mercury = 0.033 kcal/(kg °C)]
Solution:
Data: m = 500 g = 0.5 kg,
T1 = 20 °C,
T2 = 100 °C, c = 0.033 kcal/(kg . °C), Q = ?
Q = mc (T2 – T1)
= 0.5 kg × 0.033 kcal/(kg . °C) × (100 °C – 20 °C)
= 0.5 × 0.033 × 80 kcal
= 0.033 × 40 kcal
∴ Q = 1.32 kcal
Heat required = 1.32 kcal.
[Note: 1kcal/(kg-°C) = 1 cal/(g.°C)]
Question 5.
A certain mass of water at 84 °C is poured into an equal mass of water at 24 °C. What will be the resulting temperature of the mixture ?
Solution:
Data: mx = m2 = m (say),
T1 = 84 °C, T2 = 24 °C, T = ?
Heat lost by the hot water = heat gained by the cold water

Resulting temperature of the mixture = 54 °C.
Question 6.
A bucket contains 8 kg of water at 20 °C. When 4 kg of hot water is mixed with it, the temperature of the mixture becomes 40 °C. Calculate the temperature of the hot water. (Ignore the heat absorbed by the bucket.)
Solution:
Data: m1 = 8 kg, T1 = 20 °C, m2 = 4 kg, T = 40 °C, T2= ?
Heat lost by the hot water = heat gained by the cold water (ignoring the heat absorbed by the bucket)
∴ m2c (T2 – T) = m1c (T – T1)
∴ 4 kg × c × (T2 – 40°C)
= 8 kg × c × (40°C – 20°C)
∴ T2 – 40°C = 2 × 20°C = 40°C
∴ T2 = 40 °C + 40 °C = 80 °C
Temperature of the hot water = 80 °C.
![]()
Question 7.
A blacksmith plunges a 2 kg horseshoe at 400 °C into 1 kg of water at 20 °C. Find the maximum temperature of the water. [Specific heat of iron = 0.11 kcal/(kg-°C)]
Solution:
Data: mx = 2 kg,
c1 = 0.11 kcal/(kg.°C), T2 = 400 °C, m2 = 1 kg,
c2 = 1 kcal/(kg.°C), T2 = 20 °C, T = ?
Heat lost by the horseshoe = heat gained by the water
∴ m1c1 (T1 – T) = m2c2(T – T2)
∴ 2 kg × 0.11 kcal/(kg.°C) × (400 °C – T)
= 1 kg × 1 kcal/(kg.°C) × (T – 20 °C)
∴ 0.22 × (400 °C – T) = T – 20 °C
∴ 1.22 T= 108 °C
∴ T = \(\frac{108}{1.22}\)°C = 88.52 °C
Maximum temperature of the water = 88.52 °C.
![]()
Question 8.
A copper sphere of mass 500 g is heated to 100 °C and then introduced into a copper calorimeter containing 100 g of water at 20 °C. Find the maximum temperature of the mixture, if the mass of the calorimeter is 100 g and the specific heat of the calorimeter is 0.1 cal/(g.°C).
Solution:
Data: m = 500 g, c = 0.1 cal/(g.°C), T’= 100 °C, m1 = 100 g, c1 = 1 cal/(g.°C), T1 = 20°C, m2 = 100 g, c2 = 0.1 cal/(g.°C), T2 = 20 °C, T= ?
Heat lost by the sphere = heat gained by the water and the calorimeter.
∴ mc (T’ – T) = m1c1 (T – T1) + m2c2 (T – T2)
∴ 500 g × o.l cal/(g.°C) × (100 °C – T)
= 100 g × 1 cal/(g.°C) × (T – 20 °C) + 100 g × 0.1 cal/(g.°C) × (T – 20 °C)
∴ 50 (100 °C – T) = 100 × (T – 20 °C) + 10 × (T – 20 °C)
∴ 50 (100 °C – T) = 110 × (T – 20 °C)
∴ 500 °C – 5T = 11T – 220 °C
∴ 16T = 720 °C
∴ T = \(\frac{720^{\circ} \mathrm{C}}{16}\) = 45 °C
Maximum temperature of the mixture = 45 °C.
Question 9.
A metal rod 1.8 m long, increases ( in length by 1.4 mm, when heated from 0 °C to 50 °C. Find the coefficient of linear expansion of the metal.
Solution:
Data: l1 = 1.8 m, l2 – l1 = 1.4 mm = 1.4 × 10-3 m.
T1 = 0 °C, T2 = 50 °C.
l2 – l1 = l1 λ (T2 – T1)
∴ The coefficient of linear expansion of the metal is

Question 10.
A thin metal disc of surface area 500 cm2 at 0 °C is heated to 40 °C. Find the increase in the surface area of the disc. (σ = 4 × 10-5 °C -1)
Solution:
Data: A1 = 500 cm2, T1 = 0 °C,
T2 = 40 °C, σ = 4 × 10-5 °C-1, A2 – A1 = ?
The increase in the surface area of the disc is
A2 – A1 = A1σ(T2 – T1)
= (500 cm2) (4 × 10-5 °C-1) (40 °C – 0 °C)
= 500 × 4 × 10-5 × 40 = 0.8 cm2.
![]()
Question 11.
The surface area of a metal plate is 2.4 × 10-2m2 at 20 °C. When the plate is heated to 185 °C, its area increases by 0.8 cm2. Find the coefficient of areal expansion of the metal.
Solution:
Data: A1 = 2.4 × 10-2 m2,
T1 = 20 °C, T2 = 185 °C, ΔA = 0.8 cm2 = 0.8 × 10-4 m2, σ = ?
ΔA = A2 – A1 = A1 σ(T2 – T1)
∴ The coefficient of areal expansion of the metal is

Question 12.
A lead bullet has a volume of 25 cm3 at 0 °C, and 25.21 cm3 at 90 °C. Find the volumetric expansion coefficient of lead.
Solution:
Data: V1 = 25 cm3, T1 = 0 °C,
V2 = 25.21 cm3, T2 = 90 °C
T2 – T1 = 90 °C – 0 °C = 90 °C β = ?

The volumetric expansion coefficient of lead is 9.333 × 10-5 °C-1.
Example Questions for practice:
Question 1.
The temperature of a body is 30 °C. Express it in (i) degree Fahrenheit (ii) kelvin.
Answer:
86 °F, 303.15 K
![]()
Question 2.
The temperature of a body is 283.15 K. Express it in °C and °F.
Answer:
10 °C, 50 °F
Question 3.
The temperature of a body is 68 °F. Express it in °C and K.
Answer:
20 °C, 293.15 K
Question 4.
Find the heat needed to raise the temperature of 5 kg of water from 20 °C to 25 °C. Write the answer in calorie as well as joule.
Answer:
25 × 103 cal, 1.045 × 105 J
Question 5.
When a substance having mass 2 kg absorbs 2000 cal of heat, its temperature increases by 10 °C. Find the specific heat of the substance.
Answer:
0.1 cal/(g.°C)
Question 6.
Find the heat needed to raise the temperature of 100 g of a metal through 10 °C if the specific heat of the metal is 0.1 cal/g. °C.
Answer:
100 cal
![]()
Question 7.
If water of mass 80 g and temperature 40 °C is mixed with water of mass 20 g and temperature 25 °C, what will be the maximum temperature of the mixture?
Answer:
37 °C
Question 8.
A metal rod 2.5 m long, increases in length by 1.25 mm when it is heated from 10 °C to 60 °C. Find the coefficient of linear expansion of the metal.
Answer:
1 × 10-5 °C-1
Question 9.
The surface area of a metal plate is 2 × 10-2 m2 at 10 °C. When the plate is heated to 60 °C, its area increases by 0.2 m2. Find the coefficient of areal expansion of the metal.
Answer:
2 × 10-5 °C-1
Question 10.
A metal ball has volume 50 cm3 at 0 °C and 50.4 cm3 at 100 °C. Find the volumetric expansion coefficient of the metal.
Answer:
8 × 10-5 °C-1
Project:
Ref. Project. Useful information:
A bimetallic strip: A bimetallic strip consists of two strips of equal lengths but of different metals rivetted together. At room temperature the strip is straight.
Question 1.
The principle on which a bimetallic strip works:
Answer:
When two different metal strips of the same length at a given temperature are heated to the same higher temperature, they expand in different proportion.
A bimetallic strip of brass and iron is straight at room temperature. The expansion of brass is nearly 1.5 times that of iron. Hence, when this bimetallic strip is heated, it bends, making the iron side concave.
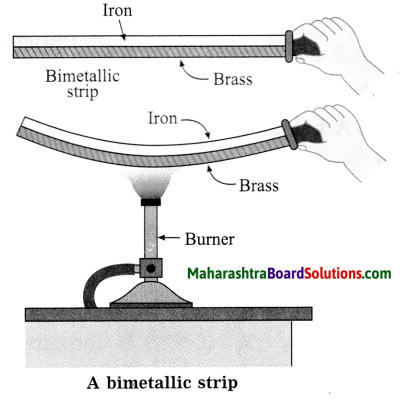
![]()
Question 2.
How a bimetallic strip is used in fire alarm:
Answer:
A bimetallic strip of brass and iron is
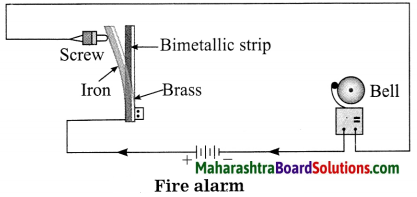
connected to a battery and an electric bell as shown in the diagram. One terminal of the bell is connected to a screw which is at a very small distance from the iron side of the strip. In case, there is an accidental fire, the bimetallic strip bends towards iron and touches the screw. Thus, the circuit is completed and the bell rings, thereby warning the people of the accidental fire.