Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 8 Continuity Ex 8.1 Questions and Answers.
11th Maths Part 2 Continuity Exercise 8.1 Questions And Answers Maharashtra Board
Question 1.
Examine the continuity of
(i) f(x) = x3 + 2x2 – x – 2 at x = -2
Solution:
Given, f(x) = x3 + 2x2 – x – 2
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
∴ f(x) is continuous at x = -2.
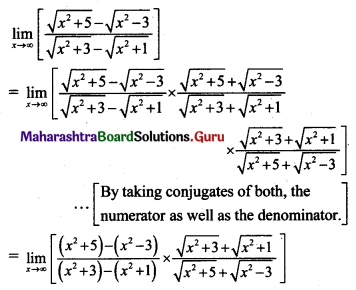
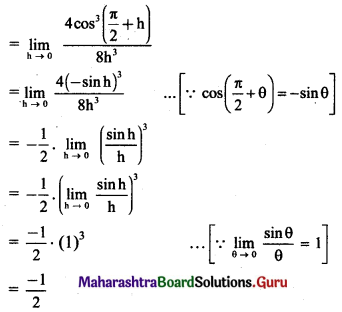
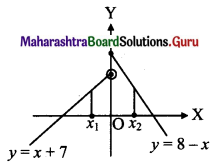
(ii) f(x) = sin x, for x ≤ \(\frac{\pi}{4}\)
= cos x, for x > \(\frac{\pi}{4}\), at x = \(\frac{\pi}{4}\)
Solution:

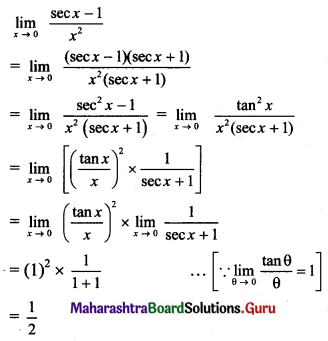
(iii) f(x) = \(\frac{x^{2}-9}{x-3}\), for x ≠ 3
= 8 for x = 3, at x = 3.
Solution:
f(3) = 8 ….(given)
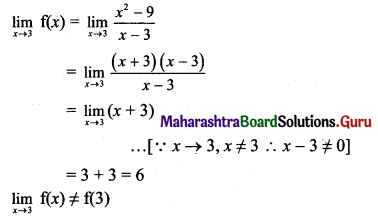
∴ f(x) is discontinuous at x = 3.
![]()
Question 2.
Examine whether the function is continuous at the points indicated against them.
(i) f(x) = x3 – 2x + 1, if x ≤ 2
= 3x – 2, if x > 2, at x = 2.
Solution:

(ii) f(x) = \(\frac{x^{2}+18 x-19}{x-1}\), for x ≠ 1
= 20, for x = 1, at x = 1.
Solution:

(iii) f(x) = \(\frac{x}{\tan 3 x}+2\), for x < 0
= \(\frac{7}{3}\), for x ≥ 0, at x = 0.
Solution:

Question 3.
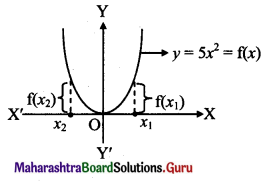
Find all the points of discontinuities of f(x) = [x] on the interval (-3, 2).
Solution:
f(x) = [x], x ∈ (-3, 2)
i.e., f(x) = -3, x ∈ (-3, -2)
= -2, x ∈ [-2, -1)
= -1, x ∈ [- 1, 0)
= 0, x ∈ [0, 1)
= 1, x ∈ [1, 2)
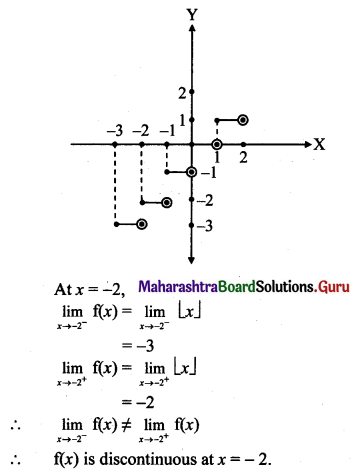
Similarly, f(x) is discontinuous at the points x = -1, x = 0, x = 1.
Thus all the integer values of x in the interval (-3, 2),
i.e., the points x = -2, x = -1, x = 0 and x = 1 are the required points of discontinuities.
Question 4.
Discuss the continuity of the function f(x) = |2x + 3|, at x = \(\frac{-3}{2}\).
Solution:


![]()
Question 5.
Test the continuity of the following functions at the points or intervals indicated against them.

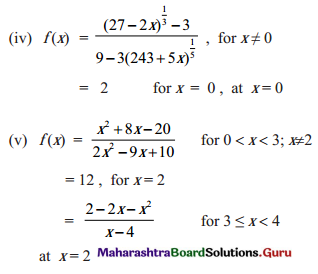
Solution:





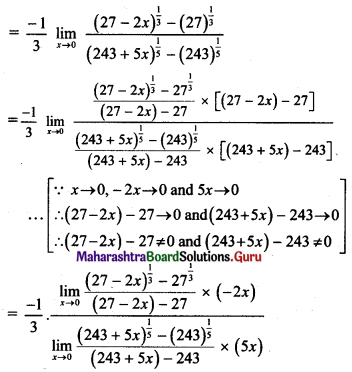


Question 6.
Identify discontinuities for the following functions as either a jump or a removable discontinuity.
(i) f(x) = \(\frac{x^{2}-10 x+21}{x-7}\)
Solution:
Given, f(x) = \(\frac{x^{2}-10 x+21}{x-7}\)
It is a rational function and is discontinuous if
x – 7 = 0, i.e., x = 7
∴ f(x) is continuous for all x ∈ R, except at x = 7.
∴ f(7) is not defined.
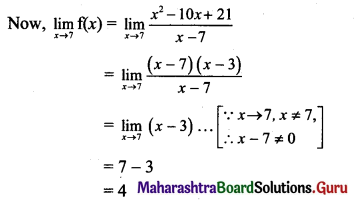
Thus, \(\lim _{x \rightarrow 7} \mathrm{f}(x)\) exist but f(7) is not defined.
∴ f(x) has a removable discontinuity.
(ii) f(x) = x2 + 3x – 2, for x ≤ 4
= 5x + 3, for x > 4.
Solution:
f(x) = x2 + 3x – 2, x ≤ 4
= 5x + 3, x > 4
f(x) is a polynomial function for both the intervals.
∴ f(x) is continuous for both the given intervals.
Let us test the continuity at x = 4.

∴ f(x) is discontinuous at x = 4.
∴ f(x) has a jump discontinuity at x = 4.
![]()
(iii) f(x) = x2 – 3x – 2, for x < -3 = 3 + 8x, for x > -3.
Solution:
f(x) = x2 – 3x – 2, x < -3 = 3 + 8x, x > -3
f(x) is a polynomial function for both the intervals.
∴ f(x) is continuous for both the given intervals.
Let us test the continuity at x = -3.

∴ f(x) is discontinuous at x = -3.
∴ f(x) has a jump discontinuity at x = -3
(iv) f(x) = 4 + sin x, for x < π = 3 – cos x for x > π.
Solution:
f(x) = 4 + sin x, x < π = 3 – cos x, x > π
sin x and cos x are continuous for all x ∈ R.
4 and 3 are constant functions.
∴ 4 + sin x and 3 – cos x are continuous for all x ∈ R.
∴ f(x) is continuous for both the given intervals.
Let us test the continuity at x = π.

But f(π) is not defined.
∴ f(x) has a removable discontinuity at x = π.
![]()
Question 7.
Show that the following functions have a continuous extension to the point where f(x) is not defined. Also, find the extension.
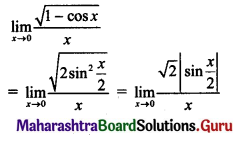
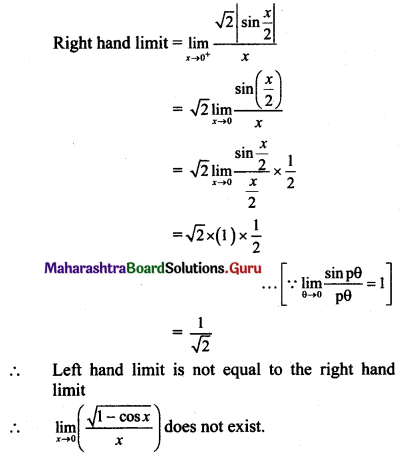
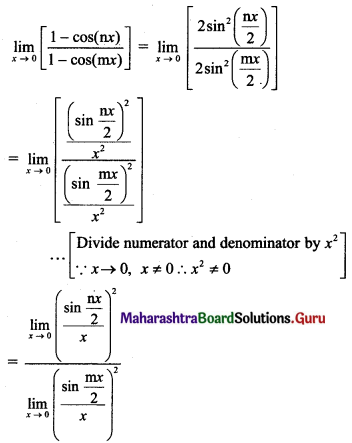
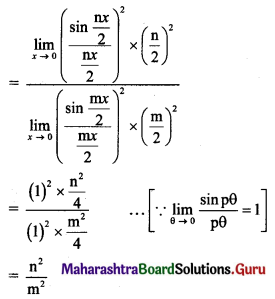
(i) f(x) = \(\frac{1-\cos 2 x}{\sin x}\), for x ≠ 0.
Solution:
f(x) = \(\frac{1-\cos 2 x}{\sin x}\), for x ≠ 0
Here, f(0) is not defined.
Consider,
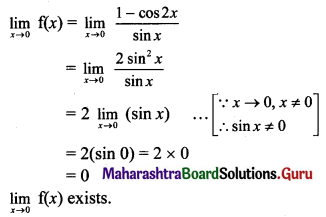
But f(0) is not defined.
∴ f(x) has a removable discontinuity at x = 0.
∴ The extension of the original function is
f(x) = \(\frac{1-\cos 2 x}{\sin x}\) for x ≠ 0
= 0 for x = 0
∴ f(x) is continuous at x = 0.
(ii) f(x) = \(\frac{3 \sin ^{2} x+2 \cos x(1-\cos 2 x)}{2\left(1-\cos ^{2} x\right)}\), for x ≠ 0.
Solution:
f(x) = \(\frac{3 \sin ^{2} x+2 \cos x(1-\cos 2 x)}{2\left(1-\cos ^{2} x\right)}\), for x ≠ 0
Here, f(0) is not defined.
Consider,

But f(0) is not defined.
∴ f(x) has a removable discontinuity at x = 0.
∴ The extension of the original function is
f(x) = \(\frac{3 \sin ^{2} x+2 \cos x(1-\cos 2 x)}{2\left(1-\cos ^{2} x\right)}\), x ≠ 0
= \(\frac{7}{2}\), x = 0
∴ f(x) is continuous at x = 0.
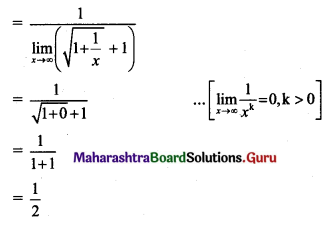
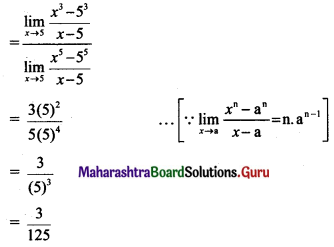
(iii) f(x) = \(\frac{x^{2}-1}{x^{3}+1}\), for x ≠ -1
Solution:
f(x) = \(\frac{x^{2}-1}{x^{3}+1}\), for x ≠ -1
Here, f(-1) is not defined.
Consider,

But f(-1) is not defined.
∴ f(x) has a removable discontinuity at x = -1.
∴ The extension of the original function is
f(x) = \(\frac{x^{2}-1}{x^{3}+1}\), x ≠ -1
= \(-\frac{2}{3}\), x = -1
∴ f(x) is continuous at x = \(-\frac{2}{3}\)
Question 8.
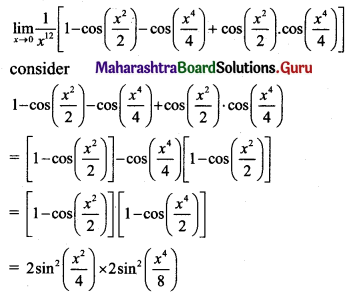
Discuss the continuity of the following functions at the points indicated against them.

Solution:
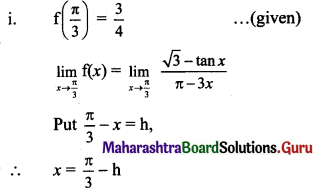


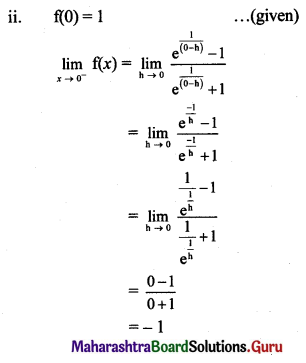
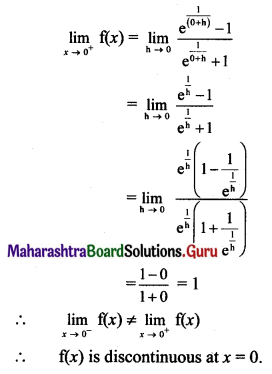

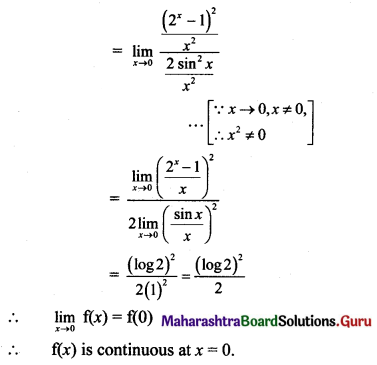
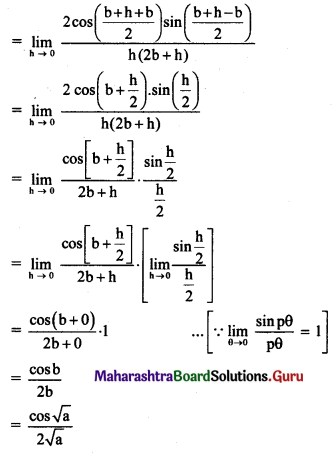
Question 9.
Which of the following functions has a removable discontinuity? If it has a removable discontinuity, redefine the function so that it becomes continuous.
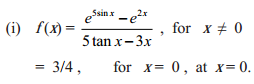

Solution:

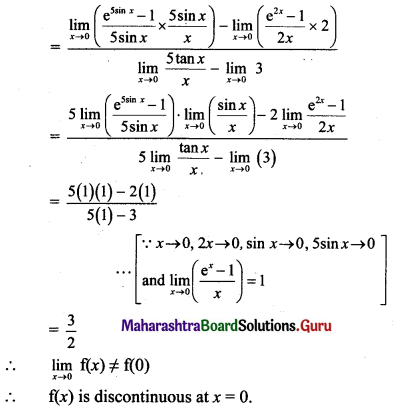









Question 10.
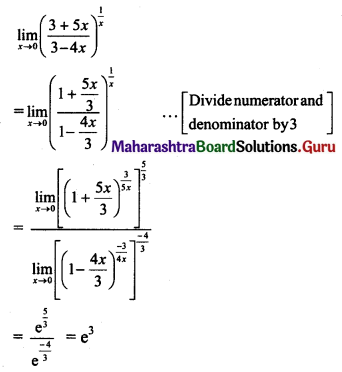
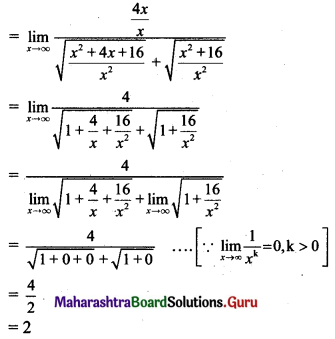
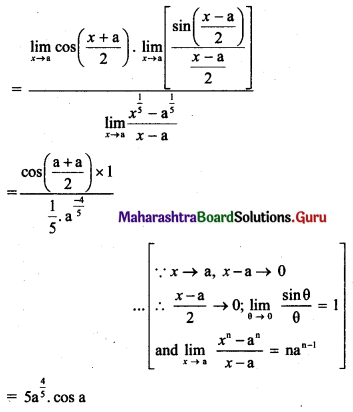
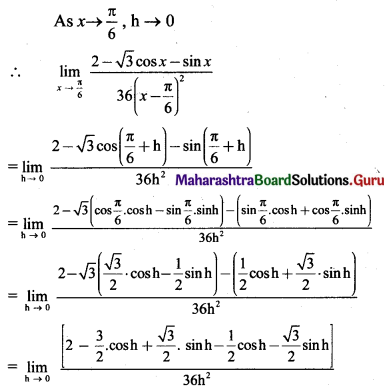
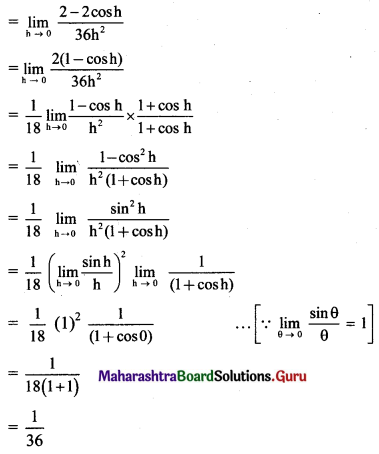
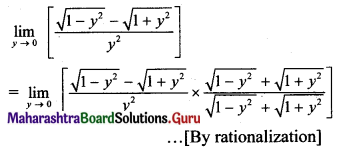
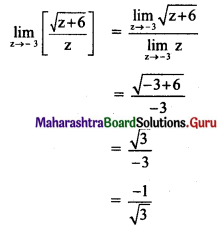
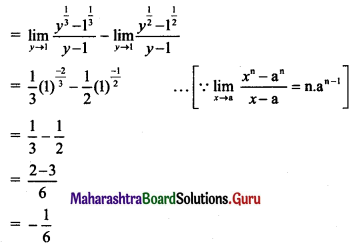
(i) If f(x) = \(\frac{\sqrt{2+\sin x}-\sqrt{3}}{\cos ^{2} x}\), for x ≠ \(\frac{\pi}{2}\), is continuous at x = \(\frac{\pi}{2}\) then find f(\(\frac{\pi}{2}\)).
Solution:
f(x) is continuous at x = \(\frac{\pi}{2}\), …..(given)

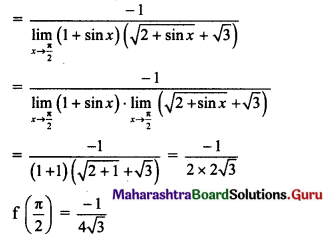
![]()
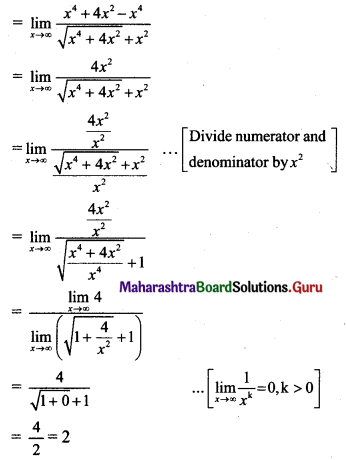
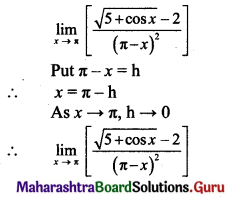
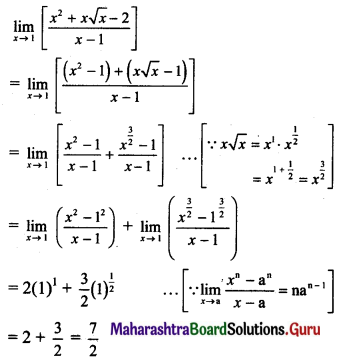
(ii) If f(x) = \(\frac{\cos ^{2} x-\sin ^{2} x-1}{\sqrt{3 x^{2}+1}-1}\) for x ≠ 0, is continuous at x = 0 then find f(0).
Solution:
f(x) is continuous at x = 0, …..(given)
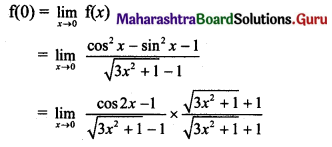

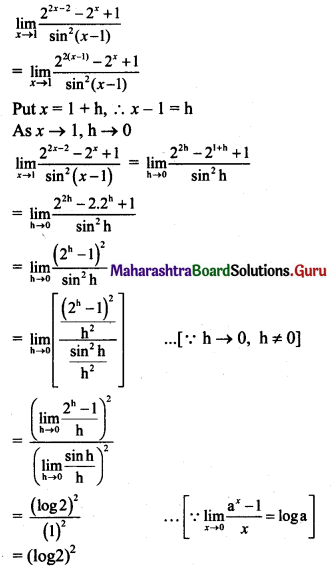
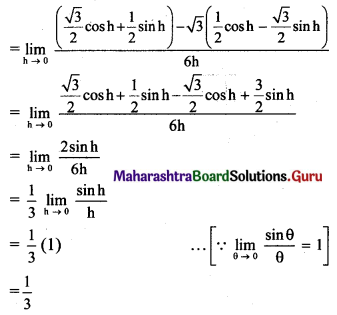
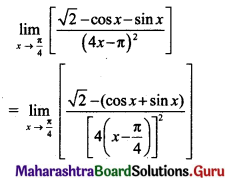
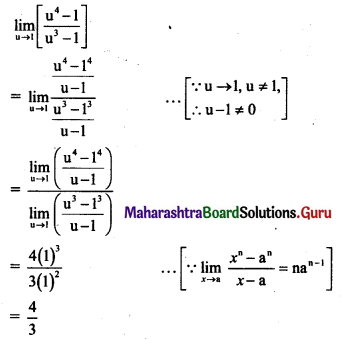
(iii) If f(x) = \(\frac{4^{x-\pi}+4^{\pi-x}-2}{(x-\pi)^{2}}\) for x ≠ π, is continuous at x = π, then find f(π).
Solution:
f(x) is continuous at x = π, …..(given)

Question 11.
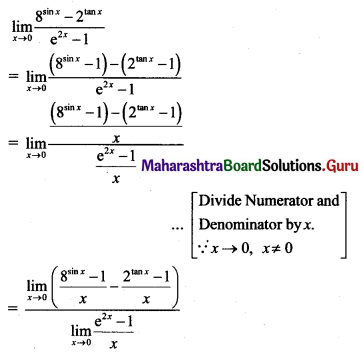
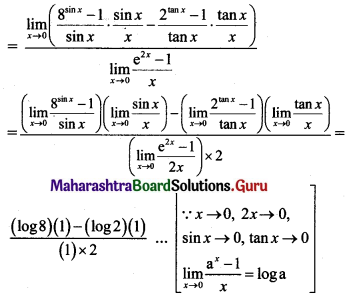
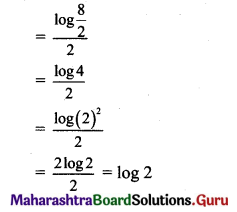
(i) If f(x) = \(\frac{24^{x}-8^{x}-3^{x}+1}{12^{x}-4^{x}-3^{x}+1}\), for x ≠ 0
= k, for x = 0
is continuous at x = 0, then find k.
Solution:
f(x) is continuous at x = 0 …..(given)

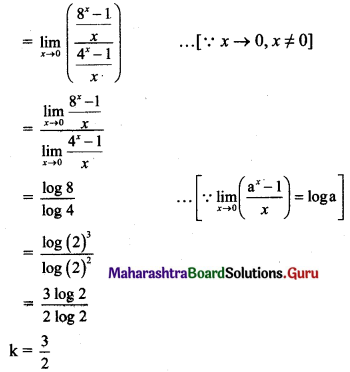
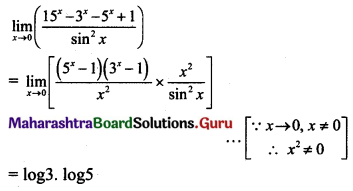
(ii) If f(x) = \(\frac{5^{x}+5^{-x}-2}{x^{2}}\), for x ≠ 0
= k, for x = 0
is continuous at x = 0, then find k.
Solution:
f(x) is continuous at x = 0 …..(given)

(iii) If f(x) = \(\frac{\sin 2 x}{5 x}\) – a, for x > 0
= 4 for x = 0
= x2 + b – 3, for x < 0
is continuous at x = 0, find a and b.
Solution:
f(x) is continuous at x = 0 ……(given)

(iv) For what values of a and b is the function
f(x) = ax + 2b + 18, for x ≤ 0
= x2 + 3a – b, for 0 < x ≤ 2 = 8x – 2, for x > 2,
continuous for every x?
Solution:
f(x) is continuous for every x …..(given)
∴ f(x) is continuous at x = 0 and x = 2.
As f(x) is continuous at x = 0,
\(\lim _{x \rightarrow 0^{-}} \mathrm{f}(x)=\lim _{x \rightarrow 0^{+}} \mathrm{f}(x)\)

∴ (2)2 + 3a – b = 8(2) – 2
∴ 4 + 3a – b = 14
∴ 3a – b = 10 …….(ii)
Subtracting (i) from (ii), we get
2a = 4
∴ a = 2
Substituting a = 2 in (i), we get
2 – b = 6
∴ b = -4
∴ a = 2 and b = -4
![]()
(v) For what values of a and b is the function
f(x) = \(\frac{x^{2}-4}{x-2}\), for x < 2
= ax2 – bx + 3, for 2 ≤ x < 3
= 2x – a + b, for x ≥ 3
continuous for every x on R?
Solution:
f(x) is continuous for every x on R …..(given)
∴ f(x) is continuous at x = 2 and x = 3.
As f(x) is continuous at x = 2,

∴ a(3)2 – b(3) + 3 = 2(3) – a + b
∴ 9a – 3b + 3 = 6 – a + b
∴ 10a – 4b = 3 …..(ii)
Multiplying (i) by 2, we get
8a – 4b = 2 ….(iii)
Subtracting (ii) from (iii), we get
-2a = -1
∴ a = \(\frac{1}{2}\)
Substituting a = \(\frac{1}{2}\) in (i), we get
4(\(\frac{1}{2}\)) – 2b = 1
∴ 2 – 2b = 1
∴ 1 = 2b
∴ b = \(\frac{1}{2}\)
∴ a = \(\frac{1}{2}\) and b = \(\frac{1}{2}\)
Question 12.
Discuss the continuity of f on its domain, where
f(x) = |x + 1|, for -3 ≤ x ≤ 2
= |x – 5|, for 2 < x ≤ 7
Solution:

Question 13.
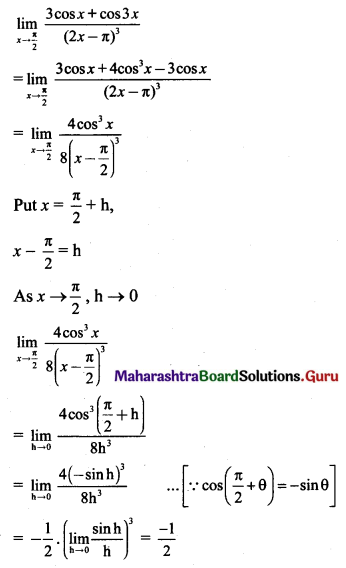
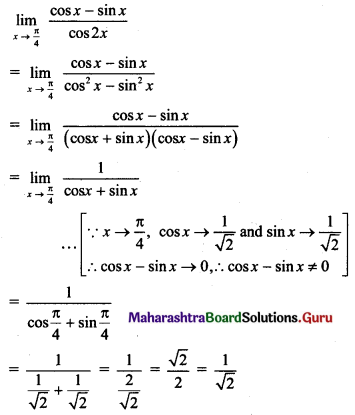
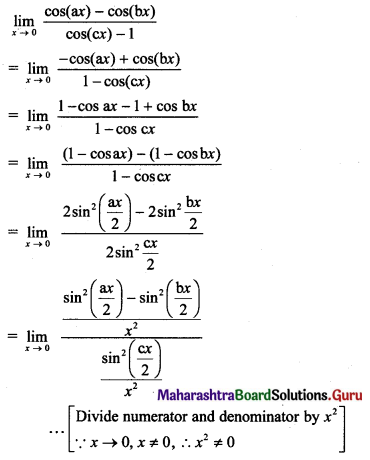
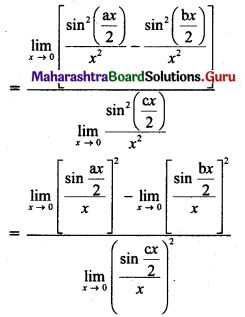
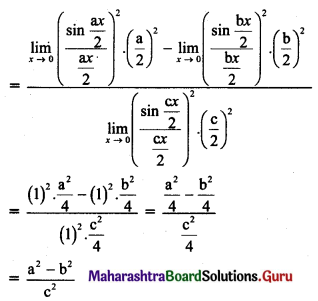
Discuss the continuity of f(x) at x = \(\frac{\pi}{4}\) where,
f(x) = \(\frac{(\sin x+\cos x)^{3}-2 \sqrt{2}}{\sin 2 x-1}\), for x ≠ \(\frac{\pi}{4}\)
= \(\frac{3}{\sqrt{2}}\), for x = \(\frac{\pi}{4}\)
Solution:


Question 14.
Determine the values of p and q such that the following function is continuous on the entire real number line.
f(x) = x + 1, for 1 < x < 3
= x2 + px + q, for |x – 2| ≥ 1.
Solution:
|x – 2| ≥ 1
∴ x – 2 ≥ 1 or x – 2 ≤ -1
∴ x ≥ 3 or x ≤ 1
∴ f(x) = x2 + px + q for x ≥ 3 as well as x ≤ 1
Thus, f(x) = x2 + px + q; x ≤ 1
= x + 1; 1 < x < 3 = x2 + px + q; x > 3
f(x) is continuous for all x ∈ R.
∴ f(x) is continuous at x = 1 and x = 3.
As f(x) is continuous at x = 1,

Subtracting (i) from (ii), we get
2p = -6
∴ p = -3
Substituting p = -3 in (i), we get
-3 + q = 1
∴ q = 4
∴ p = -3 and q = 4
![]()
Question 15.
Show that there is a root for the equation 2x3 – x – 16 = 0 between 2 and 3.
Solution:
Let f(x) = 2x3 – x – 16
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
f(2) = 2(2)3 – 2 – 16 = -2 < 0
f(3) = 2(3)3 – 3 – 16 = 35 > 0
∴ f(2) < 0 and f(3) > 0
∴ By intermediate value theorem,
there has to be point ‘c’ between 2 and 3 such that f(c) = 0.
∴ There is a root of the given equation between 2 and 3.
Question 16.
Show that there is a root for the equation x3 – 3x = 0 between 1 and 2.
Solution:
Let f(x) = x3 – 3x
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
f(1) = (1)3 – 3(1) = -2 < 0
f(2) = (2)3 – 3(2) = 2 > 0
∴ f(1) < 0 and f(2) > 0
∴ By intermediate value theorem,
there has to be point ‘c’ between 1 and 2 such that f(c) = 0.
There is a root of the given equation between 1 and 2.
Question 17.
Let f(x) = ax + b (where a and b are unknown)
= x2 + 5 for x ∈ R
Find the values of a and b, so that f(x) is continuous at x = 1.
Solution:
f(x) = x2 + 5, x ∈ R
∴ f(1) = 1 + 5 = 6
If f(x) = ax + b is continuous at x = 1, then
f(1) = \(\lim _{x \rightarrow 1}(a x+b)\) = a + b
∴ 6 = a + b where, a, b ∈ R
∴ There are infinitely many values of a and b.
![]()
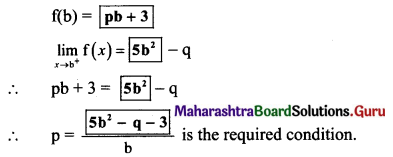
Question 18.
Activity: Suppose f(x) = px + 3 for a ≤ x ≤ b
= 5x2 – q for b < x ≤ c
Find the condition on p, q, so that f(x) is continuous on [a, c], by filling in the boxes.

Solution:
11th Standard State Board Maths Solutions






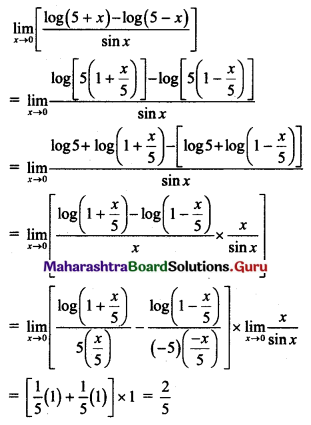
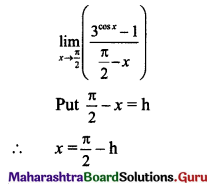
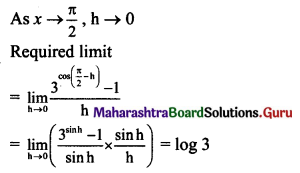

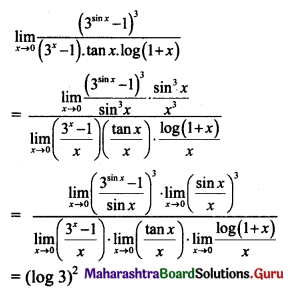
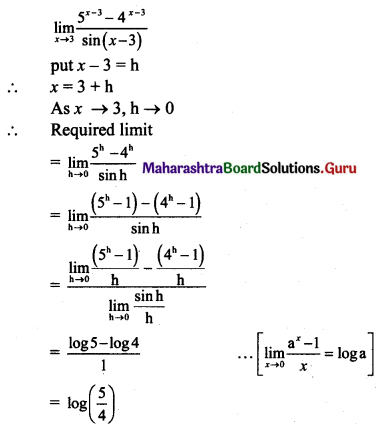
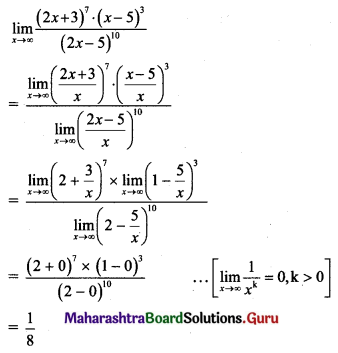


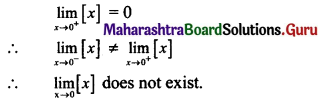


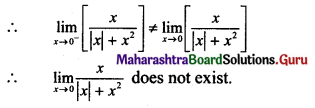

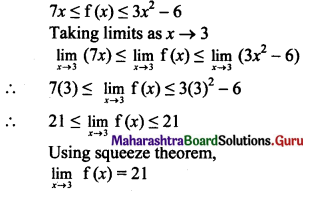

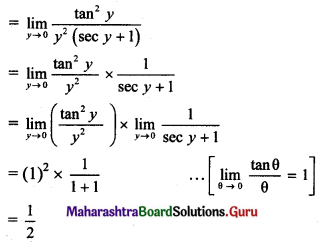

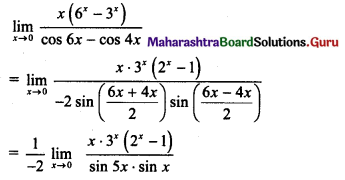











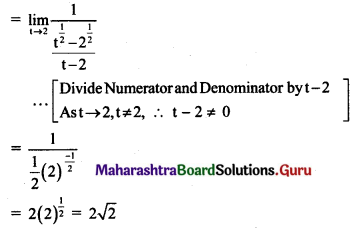







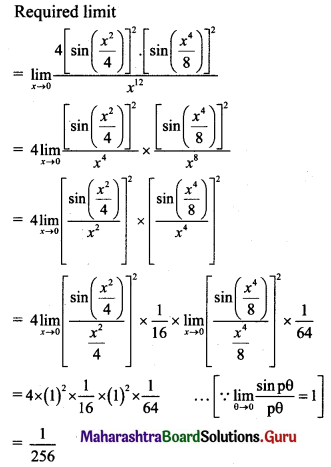


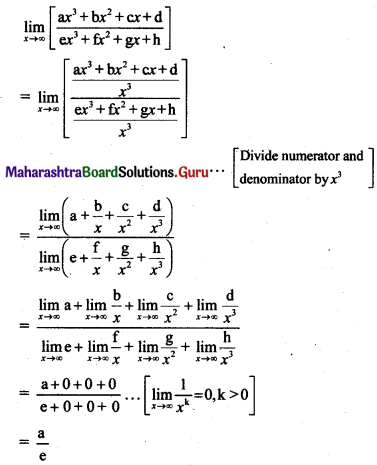

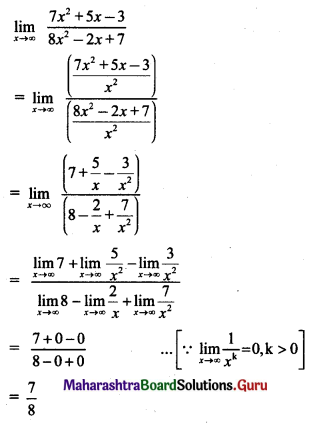
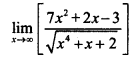








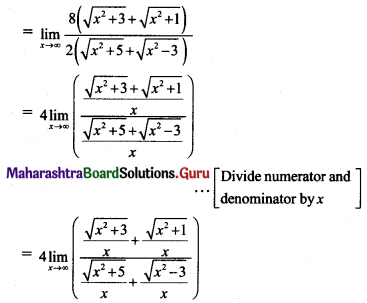
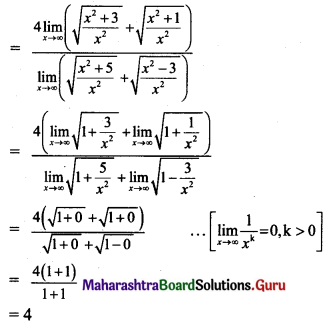
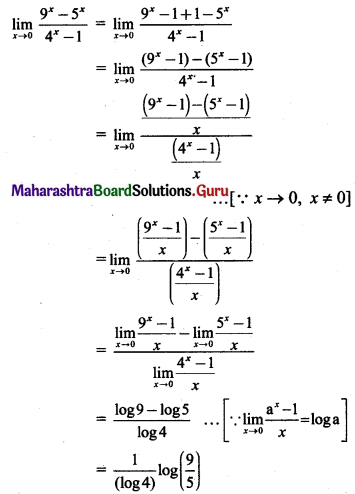

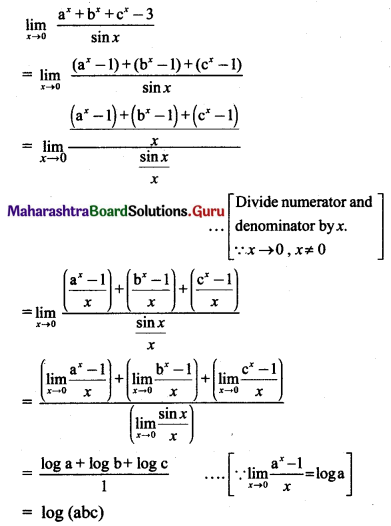
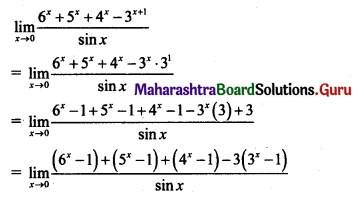


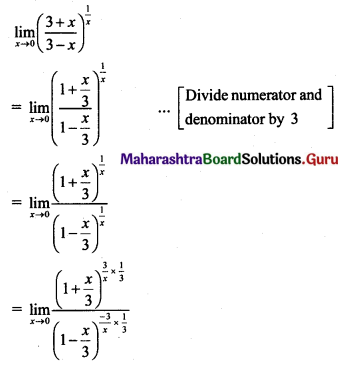
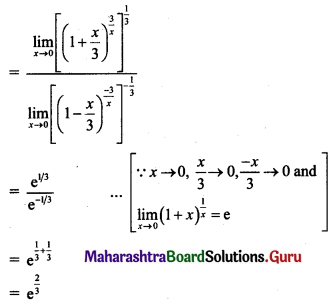

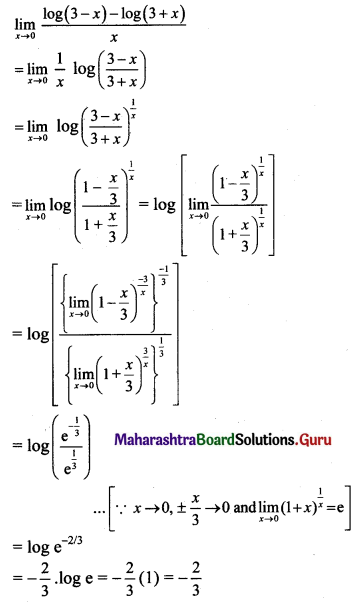


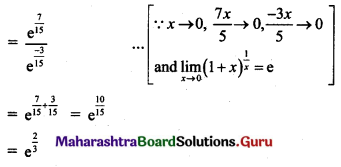

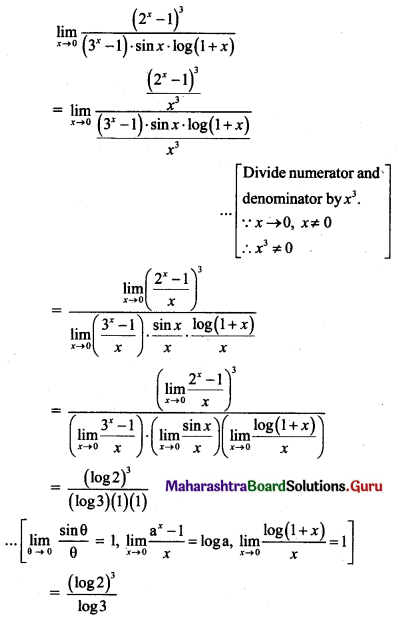



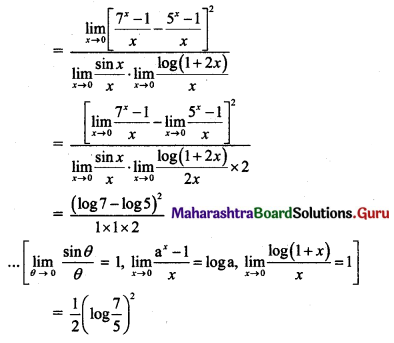

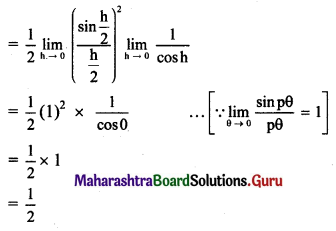
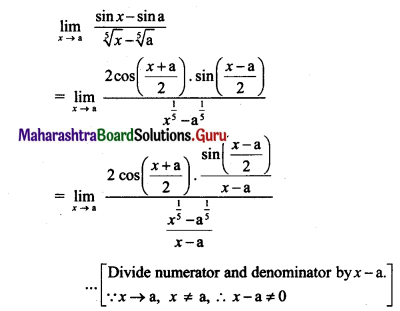









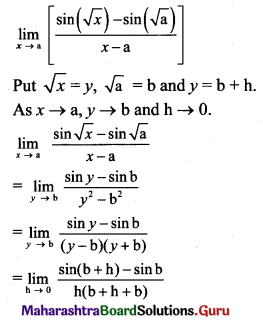

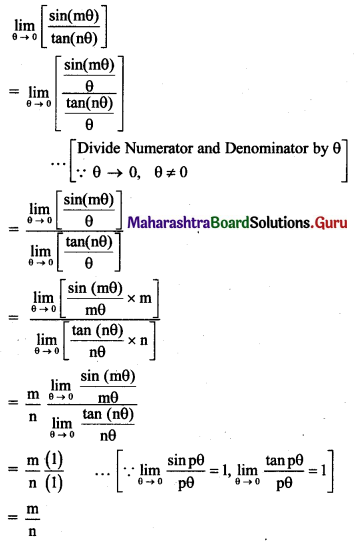
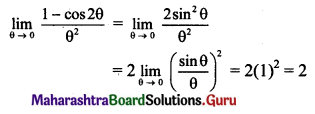
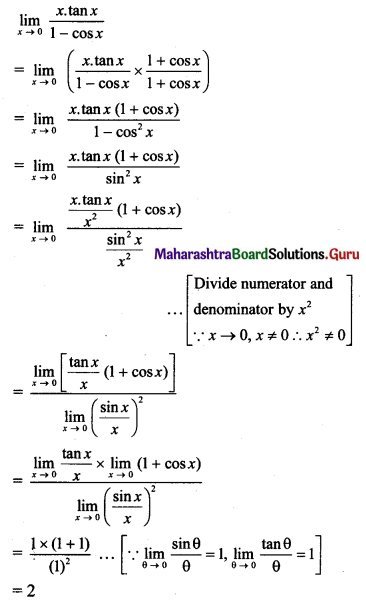


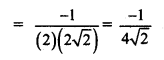

































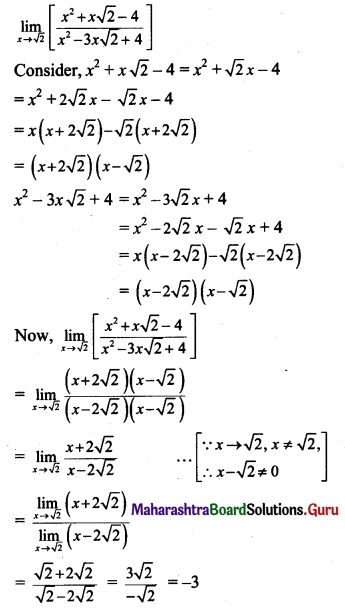

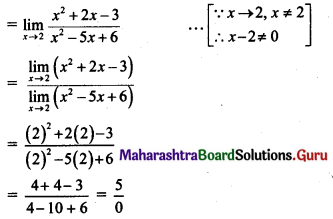











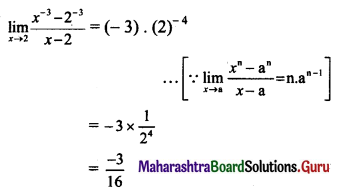








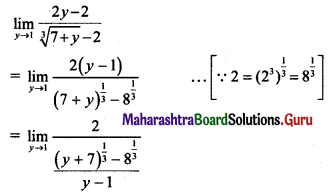






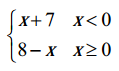
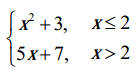 , then find
, then find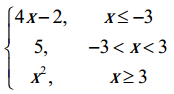 , then find
, then find