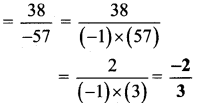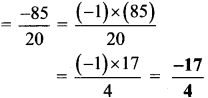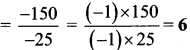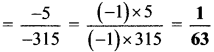Prasanna

Indices and Cube Root Class 8 Maths Chapter 3 Practice Set 3.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 3.1 8th Std Maths Answers Solutions Chapter 3 Indices and Cube Root.

Std 8 Maths Practice Set 3.1 Chapter 3 Solutions Answers

Question 1.
Express the following numbers in index form.
i. Fifth root of 13
ii. Sixth root of 9
iii. Square root of 256
iv. Cube root of 17
v. Eighth root of 100
vi. Seventh root of 30
Solution:
i. \((13)^{\frac{1}{5}}\)
ii. \((9)^{\frac{1}{6}}\)
iii. \((256)^{\frac{1}{2}}\)
iv. \((17)^{\frac{1}{3}}\)
v. \((100)^{\frac{1}{8}}\)
vi. \((30)^{\frac{1}{7}}\)

Question 2.
Write in the form ‘nth root of a’ in each of the following numbers.
i. \((81)^{\frac{1}{4}}\)
ii. \((49)^{\frac{1}{2}}\)
iii. \((15)^{\frac{1}{5}}\)
iv. \((512)^{\frac{1}{9}}\)
v. \((100)^{\frac{1}{19}}\)
vi. \((6)^{\frac{1}{7}}\)
Solution:
i. Fourth root of 81.
ii. Square root of 49.
iii. Fifth root of 15.
iv. Ninth root of 512.
v. Nineteenth root of 100.
vi. Seventh root of 6.

Maharashtra Board Class 8 Maths Chapter 3 Indices and Cube Root Practice Set 3.1 Intext Questions and Activities

Question 1.
Using laws of indices, write proper numbers in the following boxes. (Textbook pg, no. 14)
i. \({ 3 }^{ 5 }\times { 3 }^{ 2 }={ 3 }^{ \left( \right) }\)
ii. \({ 3 }^{ 7 }\div { 3 }^{ 9 }={ 3 }^{ \left( \right) }\)
iii. \(({ 3 }^{ 4 })^{ 5 }={ 3 }^{ \left( \right) }\)
iv. \(5^{ -3 }=\frac { 1 }{ { 5 }^{ \left( \right) } }\)
v. \(5^{ 0 }=\left( \right) \)
vi. \(5^{ 1 }=\left( \right) \)
vii. \((5\times 7)^{ 2 }={ 5 }^{ \left( \right) }\times { 7 }^{ \left( \right) }\)
viii. \({ \left( \frac { 5 }{ 7 } \right) }^{ 3 }=\frac { { \left( \right) }^{ 3 } }{ { \left( \right) }^{ 3 } } \)
ix. \({ \left( \frac { 5 }{ 7 } \right) }^{ -3 }={ \left( \frac { \left( \right) }{ \left( \right) } \right) }^{ 3 }\)
Solution:
i. \({ 3 }^{ 5 }\times { 3 }^{ 2 }={ 3 }^{ 7 }\)
ii. \({ 3 }^{ 7 }\div { 3 }^{ 9 }={ 3 }^{ -2 }\)
iii. \(({ 3 }^{ 4 })^{ 5 }={ 3 }^{ 20 }\)
iv. \(5^{ -3 }=\frac { 1 }{ { 5 }^{ 3 } } \)
v. \(5^{ 0 }=1\)
vi. \(5^{ 1 }=5\)
vii. \((5\times 7)^{ 2 }={ 5 }^{ 2 }\times { 7 }^{ 2 }\)
viii. \({ \left( \frac { 5 }{ 7 } \right) }^{ 3 }=\frac { { 5 }^{ 3 } }{ { 7 }^{ 3 } } \)
ix. \({ \left( \frac { 5 }{ 7 } \right) }^{ -3 }={ \left( \frac { 7 }{ 5 } \right) }^{ 3 }\)

Maharashtra Board Class 8 Maths Solutions

• Indices and Cube Root Practice Set 3.1 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.2 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.3 Class 8 Maths Solutions

Indices and Cube Root Class 8 Maths Chapter 3 Practice Set 3.2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 3.2 8th Std Maths Answers Solutions Chapter 3 Indices and Cube Root.

Std 8 Maths Practice Set 3.2 Chapter 3 Solutions Answers

Question 1.
Complete the following table.

Solution:

Question 2.
Write the following numbers in the form of rational indices.
i. Square root of 5th power of 121.
ii. Cube of 4th root of 324.
iii. 5th root of square of 264.
iv. Cube of cube root of 3.
Solution:
i. \((121)^{\frac{5}{2}}\)
ii. \((324)^{\frac{3}{4}}\)
iii. \((264)^{\frac{2}{5}}\)
iv. \((3)^{\frac{3}{3}}\)

Maharashtra Board Class 8 Maths Solutions

• Indices and Cube Root Practice Set 3.1 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.2 Class 8 Maths Solutions
• Indices and Cube Root Practice Set 3.3 Class 8 Maths Solutions

Parallel Lines and Transversals Class 8 Maths Chapter 2 Practice Set 2.3 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.3 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Std 8 Maths Practice Set 2.3 Chapter 2 Solutions Answers

Question 1.
Draw a line l. Take a point A outside the line. Through point A draw a line parallel to line l.
Solution:
Steps of construction:

1. Draw a line l and take any point A outside the line.
2. Place a set-square, such that one arm of the right angle passes through A and the other arm is on line l.
3. Place the second set-square as shown in the figure such that the vertex of the right angle is at point A.
4. Hold the two set-squares in place and draw a line parallel to line l through the edge of the second set-square. Name the line as m.

Line m is the required line parallel to line l and passing through point A.

Question 2.
Draw a line l. Take a point T outside the line. Through point T draw a line parallel to line l.
Solution:
Steps of construction:

1. Draw a line l and take any point T outside the line.
2. Place a set-square, such that one arm of the right angle passes through T and the other arm is on line l.
3. Place the second set-square as shown in the figure such that the vertex of the right angle is at point T.
4. Hold the two set-squares in place and draw a line parallel to line l through the edge of the second set-square. Name the line as m.

Line m is the required line parallel to line l and passing through point T.

Question 3.
Draw a line m. Draw a line n which is parallel to line m at a distance of 4 cm from it.
Solution:
Steps of construction:

1. Draw a line m and take any two points M and N on the line.
2. Draw perpendiculars to line m at points M and N.
3. On the perpendicular lines take points S and T at a distance 4 cm from points M and N respectively.
4. Draw a line through points S and T. Name the line as n.

Line n is parallel to line m at a distance of 4 cm from it.

Maharashtra Board Class 8 Maths Solutions

• Parallel Lines and Transversals Practice Set 2.1 Class 8 Maths Solutions
• Parallel Lines and Transversals Practice Set 2.2 Class 8 Maths Solutions
• Parallel Lines and Transversals Practice Set 2.3 Class 8 Maths Solutions

HCF and LCM Class 7 Maths Chapter 3 Practice Set 14 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 14 Answers Solutions Chapter 3 HCF and LCM.

Std 7 Maths Practice Set 14 Solutions Answers

Question 1.
Choose the right option.
i. The HCF of 120 and 150 is __
(A) 30
(B) 45
(C) 20
(D) 120
Solution:
(A) 30

Hint:
120 = 2 x 2 x 2 x 3 x 5
150 = 2 x 3 x 5 x 5
∴ HCF of 120 and 150 = 2 x 3 x 5 = 30

ii. The HCF of this pair of numbers is not 1.
(A) 13,17
(B) 29,20
(C) 40, 20
(D) 14, 15
Solution:
(C) 40, 20

Hint:
40 = 2 x 2 x 2 x 5
20 = 2 x 2 x 5
∴ HCF of 40 and 20 = 2 x 5 = 10

Question 2.
Find the HCF and LCM.
i. 14,28
ii. 32,16
iii. 17,102,170
iv. 23,69
v. 21,49,84
Solution:
i. 14 = 2 x 7
28 = 2 x 14
= 2 x 2 x 7
∴ HCF of 14 and 28 = 2 x 7
= 14
LCM of 14 and 28 = 2 x 2 x 7
= 28

ii. 32 = 2 x 16
= 2 x 2 x 8
= 2 x 2 x 2 x 4
= 2 x 2 x 2 x 2 x 2
16 = 2 x 8
= 2 x 2 x 4
= 2 x 2 x 2 x 2
∴ HCF of 32 and 16 = 2 x 2 x 2 x 2
= 16
∴ LCM of 32 and 16 = 2 x 2 x 2 x 2 x 2
= 32

iii. 17 = 17 x 1
102 = 2 x 51
= 2 x 3 x 17
170 = 2 x 85
= 2 x 5 x 17
∴ HCF of 17, 102 and 170 = 17
∴ LCM of 17, 102 and 170 = 17 x 2 x 3 x 5
= 510

iv. 23 = 23 x 1
69 = 3 x 23
∴ HCF of 23 and 69 = 23
∴ LCM of 23 and 69 = 23 x 3
= 69

v. 21 = 3 x 7
49 = 7 x 7
84 = 2 x 42
= 2 x 2 x 21
= 2 x 2 x 3 x 7
∴ HCF of 21, 49 and 84 = 7
∴ LCM of 21, 49 and 84 = 7 x 3 x 7 x 2 x 2
= 588

Question 3.
Find the LCM.
i. 36, 42
ii. 15, 25, 30
iii. 18, 42, 48
iv. 4, 12, 20
v. 24, 40, 80, 120
Solution:
i. 36, 42

∴ LCM of 36 and 42 = 2 x 3 x 2 x 3 x 7
= 252

ii. 15, 25, 30

∴ LCM of 15, 25 and 30 = 5 x 3 x 5 x 2
= 150

iii. 18, 42, 48

∴ LCM of 18,42 and 48 = 2 x 3 x 2 x 2 x 3 x 7 x 2
= 1008

iv. 4, 12, 20

∴ LCM of 4, 12 and 20 = 2 x 2 x 3 x 5
= 60

v. 24, 40, 80, 120

∴ LCM of 24, 40, 80 and 120 = 2 x 2 x 2 x 5 x 3 x 2
= 240

Question 4.
Find the smallest number which when divided by 8,9,10,15,20 gives a remainder of 5 every time.
Solution:
Here, the smallest number for division is LCM of 8, 9, 10,15 and 20.
8 = 2 x 2 x 2
9 = 3 x 3
10 = 2 x 5
15 = 3 x 5
20 = 2 x 2 x 5
LCM of given numbers = 2 x 2 x 2 x 3 x 3 x 5 = 360
∴ Required, smallest number = LCM + Remainder
= 360 + 5
= 365
∴ The required smallest number is 365.

Question 5.
Reduce the fractions \(\frac{348}{319}, \frac{221}{247}, \frac{437}{551}\) to the lowest terms.
Solution:
i.

ii.

iii.

Question 6.
The LCM and HCF of two numbers are 432 and 72 respectively. If one of the numbers is 216, what is the other?
Solution:
Here, LCM = 432, HCF = 72, First number = 216
First number x Second number = LCM x HCF
∴ 216 x Second number = 432 x 72
∴ Second number = \(\frac{432 \times 72}{216}=432 \times \frac{72}{216}=432 \times \frac{1}{3}=144\)
∴ The other number is 144.

Question 7.
The product of two two-digit numbers is 765 and their HCF is 3. What is their LCM?
Solution:
Here, HCF = 3, Product of the given numbers = 765
Now, HCF x LCM = Product of the given numbers
∴ 3 x LCM = 765
∴ LCM = \(\frac { 765 }{ 3 }\) = 255
∴ The LCM of the two two-digit numbers is 255.

Question 8.
A trader has three bundles of string 392 m, 308 m and 490 m long. What is the greatest length of string that the bundles can be cut up into without any left over string?
Solution:
The required greatest length of the string is the highest common factor (HCF) of 392, 308 and 490.
∴ 392 = 2 x 2 x 2 x 7 x 7
308 = 2 x 2 x 7 x 11
490 = 2 x 7 x 7 x 5
∴ HCF of 392, 308 and 490 = 2 x 7
= 14
∴ The required greatest length of the string is 14 m.

Question 9.
Which two consecutive even numbers have an LCM of 180?
Solution:
LCM of two consecutive even numbers = 180
But, HCF of two consecutive even numbers = 2
Now, product of the given number = HCF x LCM
= 2 x 180
= 360
To find the two consecutive even numbers, we have to factorize 360.
360 = 2 x 2 x 2 x 3 x 3 x 5
360 = (2 x 3 x 3) x (2 x 2 x 5)
= 18 x 20
∴ The two consecutive even numbers whose LCM is 180 are 18 and 20.

Class 7 Maths Solution Maharashtra Board

• Multiplication and Division of Integers Practice Set 8 Class 7 Maths Solution
• Multiplication and Division of Integers Practice Set 9 Class 7 Maths Solution
• HCF and LCM Practice Set 10 Class 7 Maths Solution
• HCF and LCM Practice Set 11 Class 7 Maths Solution
• HCF and LCM Practice Set 12 Class 7 Maths Solution
• HCF and LCM Practice Set 13 Class 7 Maths Solution
• HCF and LCM Practice Set 14 Class 7 Maths Solution

Parallel Lines and Transversals Class 8 Maths Chapter 2 Practice Set 2.2 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.2 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Std 8 Maths Practice Set 2.2 Chapter 2 Solutions Answers

Question 1.
Choose the correct alternative.
i. In the given figure, if line m || line n and line p is a transversal, then find x.

(A) 135°
(B) 90°
(C) 45°
(D) 40°
Solution:
(C) 45°

Hint:

line m || line n and line p is a transversal.
∴ m∠BFG + m∠FGD = 180°
…[Interior angles]
∴ 3x + x = 180°
∴ 4x = 180°
∴ x = \(\frac { 180 }{ 4 }\)
∴ x = 45°

ii. In the given figure, if line a || line b and line l is a transversal, then find x.

(A) 90°
(B) 60°
(C) 45°
(D) 30°
Solution:
(D) 30°

Hint:

line a || line b and line l is a transversal.
∴ m∠UVS = m∠PUV
…[Alternate angles]
= 4x
m∠UVS + m∠WVS = 180°
… [Angles in a linear pair]
∴ 4x + 2x = 180°
∴ 6x = 180°
∴ x = \(\frac { 180 }{ 6 }\)
∴ x = 30°

Question 2.
In the given figure, line p || line q. Line t and line s are transversals. Find measure of ∠x and ∠y using the measures of angles given in the figure.

Solution:

i. Consider ∠z as shown in figure.
line p || line q and line t is a transversal.
∴ m∠z = 40° …(i) [Corresponding angles]
m∠x + m∠z = 180° …[Angles in a linear pair]
∴ m∠x + 40o = 180° …[From(i)]
∴ m∠x= 180° – 40°
∴ m∠x = 140°

ii. Consider ∠w as shown in the figure.
m∠w + 70° = 180° …[Angles in a linear pair]
∴ m∠w = 180° – 70°
∴ m∠w = 110° …(ii)
line p || line q and line s is a transversal.
∴ m∠y = m∠w …[Alternate angles]
∴ m∠y =110° …[From (ii)]
∴ m∠x = 140°, m∠y = 110°

Question 3.
In the given figure, line p || line q, line l || line m. Find measures of ∠a, ∠b and ∠c, using the measures of given angles. Justify your answers.

Solution:
i. line p || line q and line l is a transversal.
∴ m∠a + 80° = 180° …[Interior angles]
∴ m∠a= 180° – 80°
∴ m∠a= 100°

ii. line l || line m and line p is a transversal.
∴ m∠c = 80° …(i) [Exterior alternate angles]

iii. line p || line q and line m is a transversal.
∴ m∠b = m∠c … [Corresponding angles]
m∠b = 80° …[From (i)]
∴ m∠a = 100°, m∠b = 80°, m∠c = 80°

Question 4.
In the given figure, line a || line b, line l is a transversal. Find the measures of ∠x, ∠y, ∠z using the given information.

Solution:
line a || line b and line l is a transversal.
∴ m∠x = 105° …(i) [Corresponding angles]

ii. m∠y = m∠x … [Vertically opposite angles]
∴ m∠y = 105° …[From (i)]

iii. m∠z + 105° = 180° …[Angles in a linear pair]
∴ m∠z = 180°- 105°
∴ m∠z = 75°
∴ m∠x = 105°, m∠y = 105°, m∠z = 75°

Question 5.
In the given figure, line p || line l || line q. Find ∠x with the help of the measures given in the figure.

Solution:

line p || line l and line IJ is a transversal.
m∠IJN = m∠JIH … [Alternate angles]
∴ m∠IJN = 40° …(i)
line l || line q and line MJ is a transversal.
m∠MJN = m∠JMK … [Alternate angles]
∴ m∠MJN = 30° …(ii)
Now, m∠x = m∠IJN + m∠MJN
…[Angle addition property]
= 40° + 30° …[From (i) and (ii)]
∴ m∠x = 70°

Maharashtra Board Class 8 Maths Chapter 2 Parallel Lines and Transversals Practice Set 2.2 Intext Questions and Activities

Question 1.
When two parallel lines are intersected by a transversal eight angles are formed. If the measure of one of these eight angles is given, can we find measures of remaining seven angles? (Textbook pg, no. 9)
Solution:
Yes, we can find the measures of the remaining angles.

In the given figure, line m || line n and line l is a transversal.
m∠a = 60°(say) …(i)
i. m∠a + m∠b = 180° …[Angles in a linear pair]
∴ 60° + m∠b =180° … [From (i)]
∴ m∠b = 180° – 60°
∴ m∠b = 120° …(ii)

ii. m∠c = m∠b …[Vertically opposite angles]
∴ m∠c = 120° .. .(iii) [From (ii)]

iii. m∠d = m∠a …[Vertically opposite angles]
∴ m∠d = 60° …(iv) [From (i)]

iv. m∠e = m∠d …[Alternate angles]
∴ m∠e = 60° … [From (iv)]

v. m∠f = m∠c …[Alternate angles]
∴ m∠f = 120° …[From (iii)]

vi. m∠g = m∠d …[Corresponding angles]
∴ m∠g = 60° … [From (iv)]

vii. m∠h = m∠c … [Corresponding angles]
∴ m∠h = 120° …[From (iii)]

Question 2.
As shown in the figure (A), draw two parallel lines and their transversal on a paper. Draw a copy of the figure on another blank sheet using a trace paper, as shown in the figure (B). Colour part Land part II with different colours. Cut out the two parts with a pair of scissors. Place, part I and part II on each angle in the figure A and answer the following questions. (Textbook pg. no. 9)

1. Which angles coincide with part I?
2. Which angles coincide with part II?

Solution:

1. ∠d, ∠f and ∠h coincide with part I.
2. ∠c, ∠e and ∠g coincide with part II.

Maharashtra Board Class 8 Maths Solutions

• Parallel Lines and Transversals Practice Set 2.1 Class 8 Maths Solutions
• Parallel Lines and Transversals Practice Set 2.2 Class 8 Maths Solutions
• Parallel Lines and Transversals Practice Set 2.3 Class 8 Maths Solutions

HCF and LCM Class 7 Maths Chapter 3 Practice Set 13 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 13 Answers Solutions Chapter 3 HCF and LCM.

Std 7 Maths Practice Set 13 Solutions Answers

Question 1.
Find the LCM:
i. 12, 15
ii. 6, 8, 10
iii. 18, 32
iv. 10, 15, 20
v. 45, 86
vi. 15, 30, 90
vii. 105, 195
viii. 12,15,45
ix. 63,81
x. 18, 36, 27
Solution:
i. 12, 15

∴ LCM of 12 and 15 = 3 x 2 x 2 x 5
= 60

ii. 6, 8, 10

∴ LCM of 6, 8 and 10 = 2 x 2 x 3 x 2 x 5
= 120

iii. 18, 32

∴ LCM of 18 and 32 = 2 x 2 x 2 x 2 x 3 x 3 x 2
= 288

iv. 10, 15, 20

∴ LCM of 10, 15 and 20 = 5 x 2 x 3 x 2
= 60

v. 45, 86

∴ LCM of 45 and 86 = 2 x 3 x 3 x 5 x 43
= 3870

vi. 15, 30, 90

∴ LCM of 15,30 and 90 = 3 x 5 x 2 x 3
= 90

vii. 105, 195

∴ LCM of 105 and 195 = 5 x 3 x 7 x 13
= 1365

viii. 12, 15, 45

∴ LCM of 12, 15 and 45 = 3 x 3 x 2 x 5 x 2
= 180

ix. 63, 81

∴ LCM of 63 and 81 = 3 x 3 x 3 x 7 x 3
= 567

x. 18, 36, 27

∴ LCM of 18, 36 and 27 = 3 x 3 x 2 x 2 x 3
= 108

Question 2.
Find the HCF and LCM of the numbers given below. Verify that their product is equal to the product of the given numbers:
i. 32, 37
ii. 46, 51
iii. 15, 60
iv. 18, 63
v. 78, 104
Solution:
i. 32 = 2 x 16
= 2 x 2 x 8
= 2 x 2 x 2 x 4
= 2 x 2 x 2 x 2 x 2 x 1
37 = 37 x 1
∴ HCF of 32 and 37 =1
LCM of 32 and 37 = 2 x 2 x 2 x 2 x 2 x 37
= 1184
HCF x LCM = 1 x 1184
= 1184
Product of the given numbers = 32 x 37
= 1184
∴ HCF x LCM = Product of the given numbers.

ii. 46 = 2 x 23 x 1
51 = 3 x 17 x 1
∴ HCF of 46 and 51 = 1
LCM of 46 and 51 = 2 x 23 x 3 x 17
= 2346
HCF x LCM = 1 x 2346
= 2346
Product of the given numbers = 46 x 51
= 2346
∴ HCF x LCM = Product of the given numbers.

iii. 15 = 3 x 5
60 = 2 x 30
= 2 x 2 x 15
= 2 x 2 x 3 x 5
∴ HCF of 15 and 60 = 3 x 5
= 15
LCM of 15 and 60 = 3 x 5 x 2 x 2
= 60
HCF x LCM = 15 x 60
= 900
Product of the given numbers = 15 x 60
= 900
∴ HCF x LCM = Product of the given numbers.

iv. 18 = 2 x 9
= 2 x 3 x 3
63 = 3 x 21
= 3 x 3 x 7
∴ HCF of 18 and 63 = 3 x 3
= 9
LCM of 18 and 63 = 3 x 3 x 2 x 7
= 126
HCF x LCM = 9 x 126
= 1134
Product of the given numbers = 18 x 63
= 1134
∴ HCF x LCM = Product of the given numbers.

v. 78 = 2 x 39
= 2 x 3 x 13
104 = 2 x 52
= 2 x 2 x 26
= 2 x 2 x 2 x 13
∴ HCF of 78 and 104 = 2 x 13
= 26
LCM of 78 and 104 = 2 x 13 x 3 x 2 x 2
= 312
HCF x LCM = 26 x 312
= 8112
Product of the given numbers = 78 x 104
= 8112
∴ HCF x LCM = Product of the given numbers.

Maharashtra Board Class 7 Maths Chapter 3 HCF and LCM Practice Set 13 Intext Questions and Activities

Question 1.
Write the tables of the given numbers and find their LCM. (Textbook pg. no. 19)
i. 6, 7
ii. 8, 12
iii. 5, 6, 15
Solution:
i. Multiples of 6 : 6, 12, 18, 24, 30, 36, 42
Multiples of 7 : 7, 14, 21, 28, 35, 42, 49
∴ LCM of 6 and 7 = 42

ii. Multiples of 8 : 8, 16, 24, 32, 40
Multiples of 12 : 12, 24, 36, 48
∴ LCM of 8 and 12 = 24

iii. Multiples of 5 : 5, 10, 15, 20, 25, 30, 35
Multiples of 6 : 6, 12, 18, 24, 30, 36
Multiples of 15 : 15, 30, 45, 60
∴ LCM of 5,6 and 15 = 30

Class 7 Maths Solution Maharashtra Board

• Multiplication and Division of Integers Practice Set 8 Class 7 Maths Solution
• Multiplication and Division of Integers Practice Set 9 Class 7 Maths Solution
• HCF and LCM Practice Set 10 Class 7 Maths Solution
• HCF and LCM Practice Set 11 Class 7 Maths Solution
• HCF and LCM Practice Set 12 Class 7 Maths Solution
• HCF and LCM Practice Set 13 Class 7 Maths Solution
• HCF and LCM Practice Set 14 Class 7 Maths Solution

Parallel Lines and Transversals Class 8 Maths Chapter 2 Practice Set 2.1 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.1 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Std 8 Maths Practice Set 2.1 Chapter 2 Solutions Answers

Question 1.
In the given figure, each angle is shown by a letter. Fill in the boxes with the help of the figure

Corresponding angles:
i. ∠p and __
ii. ∠q and __
iii. ∠r and __
iv. ∠s and __

Interior alternate angles:
v. ∠s and __
vi. ∠w and __
Solution:
i. ∠w
ii. ∠x
iii. ∠y
iv. ∠z
v. ∠x
vi. ∠r

Question 2.
Observe the angles shown in the figure and write the following pair of angles.

1. Interior alternate angles
2. Corresponding angles
3. Interior angles

Solution:

1. ∠c and ∠e; ∠b and ∠h
2. ∠a and ∠e; ∠b and ∠f; ∠c and ∠g; ∠d and ∠h
3. ∠c and ∠h; ∠b and ∠e

Maharashtra Board Class 8 Maths Solutions

• Parallel Lines and Transversals Practice Set 2.1 Class 8 Maths Solutions
• Parallel Lines and Transversals Practice Set 2.2 Class 8 Maths Solutions
• Parallel Lines and Transversals Practice Set 2.3 Class 8 Maths Solutions

HCF and LCM Class 7 Maths Chapter 3 Practice Set 10 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 10 Answers Solutions Chapter 3 HCF and LCM.

Std 7 Maths Practice Set 10 Solutions Answers

Question 1.
Which number is neither a prime number nor a composite number?
Solution:
1

Question 2.
Which of the following are pairs of co-primes?
i. 8,14
ii. 4,5
iii. 17,19
iv. 27,15
Solution:
i. Factors of 8: 1, 2, 4, 8
Factors of 14: 1, 2, 7, 14
∴ Common factors of 8 and 14: 1,2
∴ 8 and 14 are not a pair of co-prime numbers.

ii. Factors of 4: 1, 4
Factors of 5: 1, 5
∴ Common factors of 4 and 5: 1
∴ 4 and 5 are a pair of co-prime numbers.

iii. Factors of 17: 1, 17
Factors of 19: 1, 19
∴ Common factors of 17 and 19: 1
∴ 17 and 19 are a pair of co-prime numbers.

iv. Factors of 27: 1, 3, 9, 27
Factors of 15: 1, 3, 5, 15 .
∴ Common factors of 27 and 15 : 1,3
∴ 27 and 15 are not a pair of co-prime numbers.

Question 3.
List the prime numbers from 25 to 100 and say how many they are.
Solution:
29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
There are 16 prime numbers from 25 to 100.

Question 4.
Write all the twin prime numbers from 51 to 100.
Solution:

1. 59 and 61
2. 71 and 73

Question 5.
Write 5 pairs of twin prime numbers from 1 to 50.
Solution:

1. 3,5
2. 5,7
3. 11,13
4. 17,19
5. 29,31
6. 41,43

Question 6.
Which are the even prime numbers?
Solution:
2

Maharashtra Board Class 7 Maths Chapter 3 HCF and LCM Practice Set 10 Intext Questions and Activities

Question 1.
Answer the following questions. (Textbook pg. no. 15)
i. Which is the smallest prime number?
ii. List the prime numbers from 1 to 50. How many are they?
iii. Identify the prime numbers in the list below.
17, 15 ,4, 3, 1, 2, 12, 23, 27, 35, 41, 43, 58, 51, 72, 79, 91, 97.
Solution:
i. 2 is the smallest prime number.
ii. There are 15 prime numbers from 1 to 50.
They are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
iii. [17], 15 ,4, [3], 1, [2], 12, [23], 27, 35, [41], [43], 58, 51, 72, [79], 91, [97].

Class 7 Maths Solution Maharashtra Board

• Multiplication and Division of Integers Practice Set 8 Class 7 Maths Solution
• Multiplication and Division of Integers Practice Set 9 Class 7 Maths Solution
• HCF and LCM Practice Set 10 Class 7 Maths Solution
• HCF and LCM Practice Set 11 Class 7 Maths Solution
• HCF and LCM Practice Set 12 Class 7 Maths Solution
• HCF and LCM Practice Set 13 Class 7 Maths Solution
• HCF and LCM Practice Set 14 Class 7 Maths Solution

Rational and Irrational Numbers Class 8 Maths Chapter 1 Practice Set 1.4 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.4 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.

Std 8 Maths Practice Set 1.4 Chapter 1 Solutions Answers

Question 1.
The number √2 is shown on a number line. Steps are given to show √3 on the number line using √2. Fill in the boxes properly and complete the activity.

The point Q on the number line shows the number ……….
A line perpendicular to the number line is drawn through the point Q. Point R is at unit distance from Q on the line.
Right angled ∆OQR is obtained by drawing seg OR.
l(OQ) = √2, l(QR) = 1
∴By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²

Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3
Solution:
The point Q on the number line shows the number √2
A line perpendicular to the number line is drawn through the point Q. Point R is at unit distance from Q on the line.
Right angled ∆OQR is obtained by drawing seg OR.
l(OQ) = √2, l(QR) = 1
∴By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²

.. .[Taking square root of both sides]
Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3.

Question 2.
Show the number √5 on the number line.
Solution:
Draw a number line and take a point Q at 2
such that l(OQ) = 2 units.
Draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.
Draw seg OR.
∆OQR formed is a right angled triangle.
By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
= 2² + 1²
= 4 + 1
= 5
∴l(OR) = √5 units
…[Taking square root of both sides]
Draw an arc with centre O and radius OR. Mark the point of intersection of the number line and arc as C. The point C shows the number √5.

Question 3.
Show the number √7 on the number line.
Solution:
Draw a number line and take a point Q at 2 such that l(OQ) = 2 units.
Draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.
Draw seg OR.
∆OQR formed is a right angled triangle.
By Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²
= 2² + 1²
= 4 + 1
= 5
∴ l(OR) = √5 units
… [Taking square root of both sides]
Draw an arc with centre O and radius OR.
Mark the point of intersection of the number line and arc as C. The point C shows the number √5.
Similarly, draw a line CD perpendicular to the number line through the point C such that l(CD) = 1 unit.
By Pythagoras theorem,
l(OD) = √6 units
The point E shows the number √6 .
Similarly, draw a line EP perpendicular to the number line through the point E such that l(EP) = 1 unit.
By Pythagoras theorem,
l(OP) = √7 units
The point F shows the number √7.

Maharashtra Board Class 8 Maths Solutions

• Rational and Irrational Numbers Practice Set 1.1 Class 8 Maths Solutions
• Rational and Irrational Numbers Practice Set 1.2 Class 8 Maths Solutions
• Rational and Irrational Numbers Practice Set 1.3 Class 8 Maths Solutions
• Rational and Irrational Numbers Practice Set 1.4 Class 8 Maths Solutions

Multiplication and Division of Integers Class 7 Maths Chapter 2 Practice Set 9 Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 9 Answers Solutions Chapter 2 Multiplication and Division of Integers.

Std 7 Maths Practice Set 9 Solutions Answers

Question 1.
Solve
i. (-96) ÷ 16
ii. 98 ÷ (-28)
iii. (-51) ÷ 68
iv. 38 ÷ (-57)
v. (-85) ÷ 20
vi. (-150) ÷ (-25)
vii. 100 ÷ 60
viii. 9 ÷ (-54)
ix. 78 ÷ 65
x. (-5) ÷ (-315)
Solution:
i. (-96) ÷ 16

ii. 98 ÷ (-28)

iii. (-51) ÷ 68

iv. 38 ÷ (-57)

v. (-85) ÷ 20

vi. (-150) ÷ (-25)

vii. 100 ÷ 60

viii. 9 ÷ (-54)

ix. 78 ÷ 65

x. (-5) ÷ (-315)

Question 2.
Write three divisions of integers such that the fractional form of each will be \(\frac { 24 }{ 5 }\).
Solution:

1. \(\frac{24}{5}=\frac{24 \times 1}{5 \times 1}=\frac{24}{5}=24 \div 5\)
2. \(\frac{24}{5}=\frac{24 \times 2}{5 \times 2}=\frac{48}{10}=48 \div 10\)
3. \(\frac{24}{5}=\frac{24 \times(-10)}{5 \times(-10)}=\frac{-240}{-50}=(-240) \div(-50)\)

Question 3.
Write three divisions of integers such that the fractional form of each will be \(\frac { -5 }{ 7 }\).
Solution:

1. \(\frac{-5}{7}=\frac{-5 \times 2}{7 \times 2}=\frac{-10}{14}=(-10) \div 14\)
2. \(\frac{-5}{7}=\frac{-5 \times(-5)}{7 \times(-5)}=\frac{25}{-35}=25 \div(-35)\)
3. \(\frac{-5}{7}=\frac{-5 \times 7}{7 \times 7}=\frac{-35}{49}=(-35) \div 49\)

Question 4.
The fish in the pond below, carry some numbers. (Choose any 4 pairs and carry out four multiplications with those numbers. Now, choose four other pairs and carry out divisions with these numbers.
Examples:
i. (-13) × (-15) = 195
ii. (-24) ÷ 9 = \(\frac{-24}{9}=\frac{-8}{3}\)

Solution:

1. (-13) × 9 = -117
2. 12 × 13 = 156
3. 9 × (-37) = -333
4. (-15) × (-8) = 120
5. \((-28) \div 12=\frac{-28}{12}=\frac{(-1) \times(28)}{12}=\frac{-7}{3}\)
6. \(12 \div 9=\frac{12}{9}=\frac{4}{3}\)
7. \(9 \div(-24)=\frac{9}{-24}=\frac{9}{(-1) \times 24}=\frac{-3}{8}\)
8. \((-18) \div(-27)=\frac{-18}{-27}=\frac{(-1) \times 18}{(-1) \times 27}=\frac{2}{3}\)

Note: Problems 2, 3 and 4 have many answers. Students may write answers other than the ones given.

Class 7 Maths Solution Maharashtra Board

• Multiplication and Division of Integers Practice Set 8 Class 7 Maths Solution
• Multiplication and Division of Integers Practice Set 9 Class 7 Maths Solution
• HCF and LCM Practice Set 10 Class 7 Maths Solution
• HCF and LCM Practice Set 11 Class 7 Maths Solution
• HCF and LCM Practice Set 12 Class 7 Maths Solution
• HCF and LCM Practice Set 13 Class 7 Maths Solution
• HCF and LCM Practice Set 14 Class 7 Maths Solution