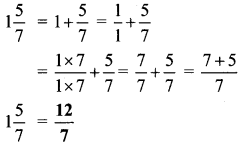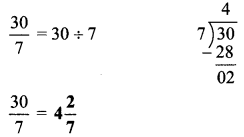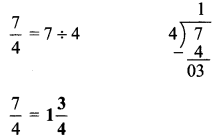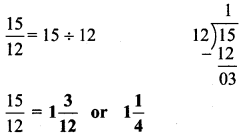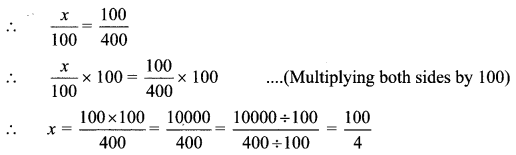Prasanna

Balbharti Maharashtra State Board Class 9 Geography Solutions Chapter 5 Precipitation Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Geography Solutions Chapter 5 Precipitation

Class 9 Geography Chapter 5 Precipitation Textbook Questions and Answers

1. Identify the precipitation type with the help of the description given:

(a) It is the main source of the water that you use. Sometimes it is torrential and sometimes continuous. Most of the agriculture in India is dependent on it.
(b) It seems as if water droplets are floating in the atmosphere. In London, one cannot see the Sun till the afternoon during winters because of this phenomenon.
(c) It never precipitates like this in equatorial areas. Precipitation in the solid form sometimes causes damage to the crops.
(d) A white cotton-like layer spreads on the earth’s surface. Because of this form of precipitation, the State of Jammu and Kashmir has to change its capital in winters. In Maharashtra, it does not precipitate like this.
Answer:
(a) rainfall
(b) fog
(c) hail
(d) snow

2. Look at the following pictures and identify the correct rainfall type.

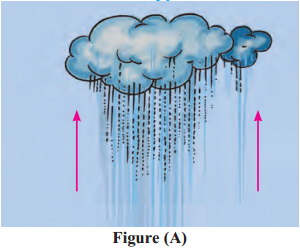
Answer:
Convectional rainfall

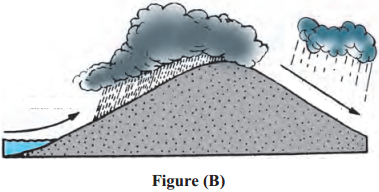
Answer:
Orographic rainfall

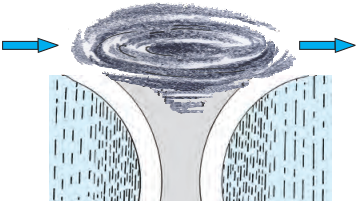
Answer:
Cyclonic rainfall

3. Look at the figures above and answer the following questions:

Question 1.
In fig B, on which side of the mountain is it raining more?
Answer:
The windward side is receiving more rainfall.

Question 2.
Shade the rain shadow region in fig B and name it.
Answer:
Students to show the leeward side in the picture.

Question 3.
What is the difference between A and C?
Answer:
In figure 5.4 i.e. convectional rainfall the hot air rises upwards and then the air cools and begins to condense and due to continuous condensation rainfall occurs. Here rainfall is accompanied by lightning and thunder.

In figure 5.6 , i.e. cyclonic rainfall, air from surrounding regions comes towards the centre of the cyclone and starts moving upwards. As it rises, the temperature of the air reduces, condensation occurs and rainfall takes place.

Question 4.
Stormy winds and floods are associated with which rainfall type?
Answer:
Stormy winds and floods are associated with Cyclonic rainfall.

Question 5.
What type of rainfall occurs in Singapore?
Answer:
Cyclonic rainfall occurs in Singapore.

4. Identify the odd man out:

Question 1.
Orographic rainfall, acid rain, cyclonic rainfall, convectional rainfall
Answer:
Acid rain

Question 2.
Snowfall, rainfall, hailstones, dew
Answer:
Dew

Question 3.
Thermometer, rain gauge, anemometer, measuring jar
Answer:
Measuring jar

5. Answer in brief:

Question 1.
In what ways does precipitation occur on the earth?
Answer:
Precipitation means water falls in the solid or liquid state from the clouds to the earth surface. Snow, hailstorms, rainfall are the major forms of precipitation.

(i) Snow:
Answer:

• When the temperature in the atmosphere falls below the freezing point the water vapour directly turns into snowflakes. This is called sublimation.
• Hence the vapour in the form of gas transform into solid snow. Precipitation in the form of solid particles is known as snowfall.
• As snow is in the solid form. It does not run like water and layers of the snow get deposited on the top of the others and when the snow melts the region gets fresh water.

(ii) Hail:

• When there is lot of heat on the earth’s surface, the upward air flow blows at a greater speed. Because of this upward flow, the temperature of air reduces and the condensation of the water vapour takes place, and dark clouds are formed.
• Because of the upward movement of the air, these water droplets go at higher altitude and solidify forming hailstones.
• As the hailstones are heavy, they fall toward the earth’s surface because of gravity. The crops may get destroyed and loss of life and property may occur.
• Hailstones occurs in summer in India, Africa and in some parts of south east Asia.

(iii) Rainfall:

• We get water generally in the form of rainfall. The temperature of the air with water vapour reduces when it goes higher and condensation of the vapour occurs.
• Clouds formed with the condensed water droplets and dust particles accumulate.
• As these water droplets increase in the size, they cannot float in the air anymore because of their weight. They come down as rainfall
• The different types of rainfall are: Convectional rainfall, Orographic rainfall and Cyclonic rainfall.

(iv) Fog, dew and frost:

• When the condensation or solidification of the water vapour in the atmosphere occurs near the earth’s surface, it leads to the formation of fog, dew and frost.

Question 2.
Comment on the rainfall occurring in the rain shadow area.
Answer:

• The winds coming from lakes or seas are moisture-laden and they are obstructed by the high mountain ranges coming in their way
• They start going upwards along the slope of the moutains. The temperature of these winds drop and condensation occurs and rainfall takes place.
• This rainfall takes place because of the obstruction of the mountains which results in the condensation of water vapour.
• The windward side of the mountain gets more rain; the amount of vapour in the air reduces after crossing the mountain and the moisture-holding capacity of the air increases.
• The leeward side of the mountain gets lesser rainfall as compared to windward side.
• Thus, the leeward side area is identified as rain shadow area as it recieves meagre rainfall.

Question 3.
Which type of rainfall occurs in most of the world? Why?
Answer:

• Orographic rainfall occurs in most parts of the world.
• Convectional rainfall is regional in nature.
• There is a certainty in the convectional rainfall occurring in the equatorial areas.
• Comparatively, the orographic and cyclonic rainfall is less certain.
• And therefore, such areas are prone to very heavy rainfall, floods or droughts frequently.

Question 4.
If condensation occurs closer to the earth’s surface, what types of forms become visible?
Answer:
If condensation and solidification of the water vapour in the atmosphere closer to the earth surface are visible, they are in the form of fog, dew or frost.

(i) Fog:

• The temperature of the layers of the air near the surface of the earth reduces. As the temperature reduces, water vapour condenses.
• In this process the water vapour turns into microscopic water particles and float in the air.
• When the density of these droplets in the air increases it leads to the formation of fog

(ii) Dew:

• When moisture-laden air near the earth surface comes in contact with very cold objects condensation of water vapour takes place.
• They turn into very small water droplets and stick to the surface of cold objects, e.g. eg: leaves and this is called dew.

(iii) Frost:

• When the temperature of the air reaches less then 0 degree Celcius the water droplet stuck to the surface of the cold objects and freezes.
• This frozen water droplet is called as frost.

Question 5.
What precautions should be taken while measuring rainfall?
Answer:

• Rainfall is an important source of water on planet earth and rainfall is formed because of changes in the temperature of the air with water vapour.
• The instrument that is used to measure rainfall is called rain gauge.
• The funnel i.e. used for measuring rain has a specific diameter and the rain falling in this funnel is collected in bottle fitted in the gauge.
• The collected water is then measured with the help of measuring jar. In the areas of heavy rainfall, the reading of the rain with rain gauge should be taken every three hours. The measuring jar reads rain in millimetres
• The gauge has to be kept on open ground on 30cm high flat-mount.
• So that the rain water is collected without any obstruction.

6. Distinguish between

Question 1.
Dew and frost
Answer:

	Dew		Frost
(i)	When moisture-laden air near the earth’s surface comes into contact with very cold objects, condensation of vapour takes place into small water droplets called dew.	(i)	If the temperature of the air is less then CPC, the water droplets stuck to the surface of cold objects, freezes forming frost.
(ii)	Water vapour condenses and forms droplets of water.	(ii)	Water droplets stuck to cold surface turns to frozen water droplets.
(iii)	Dew sticks to the cold object but does not freeze.	(iii)	It sticks to the cold object and freeze.

Question 2.
Snow and hail
Answer:

	Snow		Hail
(i)	Precipitation in the form of solid particles of snow is known as snow fall.	(i)	Precipitation in the form of frozen water droplets falling rapidly to the ground is know as hail.
(ii)	The fall of temperature in the atmosphere below the freezing point causes snow fall	(ii)	Extreme heat on the surface of the earth initiates the process of hail formation.
(iii)	Heavy accumulation of snow can collapse the transportation and communication system of the area.	(iii)	It destroys crops and causes loss of life an

Class 9 Geography Chapter 5 Precipitation Intext Questions and Answers

Can you tell?

Question 1.
The blade of grass look like this in winter mornings. From where does the water on the blades of grass come?

Answer:

1. The blade of grass looks like this in winter mornings because of dew. These are small water droplets.
2. The dew is formed in winter because moisture-laden air near the earth surface comes in contact with cold objects due to which condensation of vapour takes place, turning into small water droplets.

Question 2.
Snow is found everywhere in the winters in Kashmir.
Answer:
Snow is found everywhere in winters of Kashmir because Kashmir is located at a higher altitude where the temperature falls below freezing point. Hence water vapour directly turn into snowflakes leading to snowfall.

Question 3.
Why isn’t snow found in our surroundings?
Answer:
Because we have a moderate temperature and we are closer to the sea, snow is not found in our surroundings.

Question 4.
Generally, it rains between June and September in our region.
Answer:
We get rainfall between June and September, in our region when the moisture-laden south-west monsoon winds are obstructed by the Western Ghats leading to orographic rainfall.

Question 5.
How do the rain droplets form?
Answer:
Clouds form when condensed water droplets and dust particles accumulate forming large rain droplets.

Question 6.
In London, there is a fog like this till the afternoon in the winters.
Answer:
In London there is fog till the afternoon in winters because London is far away from equator and it has temperate oceanic climate and they have cool summers.

Question 7.
We do not have fog until afternoons in summers.
Answer:
We do not have fog until afternoons in summer because we are near to equator and we have tropical climate and hot summers.

Question 8.
Sometimes hailstones destroy the standing crops in the field.
Answer:
Hailstones are solid and heavy in nature and they hit the earth due to gravity and this is the reason they destroy the crops in the field.

Question 9.
Why don’t we get hailstones frequently?
Answer:
For the formation of hailstones the following 2 conditions are required:

• Intense heating which results in upwards air flow.
• The decrease in air temperature at higher layers of the atmosphere.
• As India is a tropical country, we do not find cooler air at higher levels because of the intense heating of land.

Think about it.

Question 1.
We use a raincoat or umbrella to protect ourselves from rainfall. What will you use to protect yourself from severe hailstorms?
Answer:
If a person is outside without any coverage, he needs to seek shelter immediately, making sure to protect his head from hailstones.

Question 2.
Because of the conventional processes, convectional rainfall occurs in the afternoon in equational areas. But why doesn’t it rain in afternoons in the oceanic areas of the equatorial belt?
Answer:
One of the necessary conditions of convectional rainfall is intense heating of surface which causes air to expand and rise. Since land heats up faster than water, it rains only on the land in the equatorial regions and not in the oceanic areas.

Question 3.
Why are the areas of high rainfall situated in tropical areas?
Answer:

• Tropical areas receive direct rays of the Sun almost throughout the year. Hence the rate of evaporation1 is high here.
• The tropical region receives convectional rainfall throughout the year and also orographic rainfall is experienced here.
• Thus areas of high rainfall are situated in the tropical area.

Class 9 Geography Chapter 5 Precipitation Additional Important Questions and Answers

Complete the statements choosing the correct option from the bracket:

Question 1.
……………. part of the earth’s surface is full of water.
(a) 30.7%
(b) 4.09%
(c) 60.5%
(d) 70.8%
Answer:
(d) 70.8%

Question 2.
When the temperature in the atmosphere falls below the freezing point and the water vapour directly turns into snowflakes, the process is called as ……………..
(a) sublimation²
(b) frostbite³
(c) carbonation
(d) convection
Answer:
(a) sublimation

Question 3.
In areas located at higher altitudes and high latitudes, where the temperatures are below 0°C get precipitation in the form of ………….
(a) dew
(b) rain
(c) snow
(d) hail
Answer:
(c) snow

Question 4.
Because of ………………. crops may get destroyed and loss of life and property may occur.
(a) dew
(b) rain
(c) snow
(d) hail
Answer:
(d) hail

Question 5.
Hails do not occur in ……………… areas.
(a) temperate
(b) equatorial
(c) landlocked
(d) mountainous
Answer:
(b) equatorial

Question 6.
In equatorial areas, …………. type of rainfall occurs almost daily in the afternoons.
(a) frontal
(b) convectional
(c) cyclonic
(d) orographic
Answer:
(b) convectional

Question 7.
…………… rainfall occurs because of obstruction from high mountain ranges.
(a) Frontal
(b) Convectional
(c) Cyclonic
(d) Orographic
Answer:
(d) orographic

Question 8.
Cyclonic rainfall occurs more in …………… zones.
(a) temperate
(b) equatorial
(c) torrid
(d) polar
Answer:
(a) temperate

Question 9.
…………… rainfall occurs in most of the parts in the world.
(a) Frontal
(b) Convectional
(c) Orographic
(d) Cyclonic
Answer:
(c) orographic

Question 10.
Snowfall can also be measured with the help of ……………
(a) hygrometer
(b) rain gauge
(c) barometer
(d) anemometer
Answer:
(b) rain gauge

Question 11.
A layer of ice is equivalent to 10mm of rainfall.
(a) 10mm
(b) 50mm
(c) 100mm
(c) 120mm
Answer:
(c) 120mm

Question 12.
When moisture-laden air near the earth’s surface comes in contact of very cold objects and form water droplets which stick to the surface of the cold objects is formed.
(a) dew
(b) frost
(c) hail
(d) fog
Answer:
(a) dew

Question 13.
If the temperature of the air reaches less than 0°C, the water droplets stuck to the surfaces of cold objects freeze and form
(a) dew
(b) frost
(c) hail
(d) fog
Answer:
(b) frost

Question 14.
If precipitation does not take place, then conditions of arise.
(a) floods
(b) hail
(c) snowstorm
(d) drought
Answer:
(d) drought

Question 15.
Visibility reduces because of
(a) floods
(b) drought
(c) fog
(d) dew
Answer:
(c) fog

Match the column:

Question 1.

Column A	Column B
(1) Snowflakes	(a) upward air flow
(2) Hailstones	(b) sublimation
(3) Dew	(c) microscopic water particles floating in the air
(4) Fog	(d) condensation4 on cold objects

Answer:
(1 – b),
(2 – a),
(3 – d),
(4 – c)

Question 2.

Column A	Column B
(1) Orographic rainfall (2) Convectional Rainfall (3) Cyclonic Rainfall	(a) Daily in equatorial areas (b) More in temperate zones (c) Mountain barrier

Answer:
(1 – c),
(2 – a),
(3 – b)

Answer in one sentence:

Question 1.
What percentage of the earth’s surface is covered with water?
Answer:
70.8% of the earth’s surface is covered with water.

Question 2.
Why do we see different forms of condensation?
Answer:
Different forms of condensation are seen due to changes in atmospheric conditions.

Question 3.
What is precipitation?
Answer:
When water falls in the solid or liquid state from the clouds to the ground, it is called as precipitation.

Question 4.
Name the major forms of precipitation.
Answer:
Snow, hailstones and rainfall are the major forms of precipitation.

Question 5.
Explain the process of sublimation.
Answer:
When the temperature in the atmosphere falls below the freezing point, water vapour directly turns into snowflakes this process is called sublimation.

Question 6.
In India, hails occur in which season?
Answer:
Hails occur in summer reason in India.

Question 7.
Why don’t hails occur in cold zones?
Answer:
Hails do not occur in cold zones because of lack of upward flow.

Question 8.
Why don’t hails occur in equatorial areas?
Answer:
Hails do not occur in equatorial areas because of the heat in the atmosphere.

Question 9.
Which type of rainfall occurs because of obstruction of mountain?
Answer:
Orographic rainfall occurs because of obstruction of mountains.

Question 10.
Convectional rainfall is mainly experienced in which region?
Answer:
Convectional rainfall is mainly experienced in equatorial region.

Question 11.
What is a Cyclone?
Answer:
Cyclone is a specific air formation when the pressure at an area is less than the surrounding regions.

Question 12.
What is acid rain?
Answer:
Precipitation of water with dissolved acids is called acid rain.

Study the rainfall map of the world given below and answer the following question:

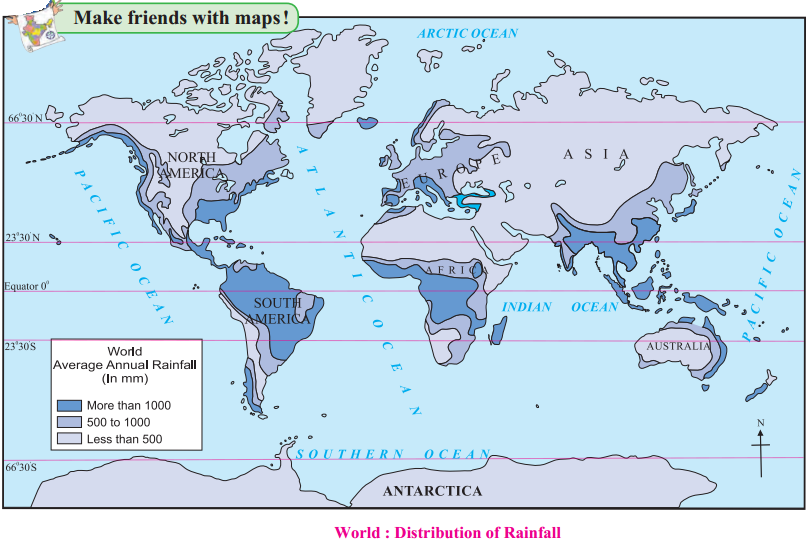
Question 1.
Which region experiences more rainfall?
Answer:
The tropical region experiences more rainfall.

Question 2.
What is the reason for low rainfall in the Central Peninsular India?
Answer:
The Central Peninsular India falls on the leeward side of the Western Ghats and hence a rain shadow region is formed here.

Question 3.
Why does the eastern part of Central African continent gets less rainfall than the western part despite its location close to the equator?
Answer:

• Eastern part of the African Continent is a rain shadow region of westerly monsoon winds whereas the western part lies on the windward side and gets more rain.
• The eastern part of Africa also comes under the influence of the North east trade winds but still receive less rains as they are dry winds originating from the land.

Question 4.
Why does the amount of high rainfall in the western part of the European continent reduce in the eastern part?
Answer:
There are many mountain ranges in the western part of Europe. These obstruct the rain-bearing clouds coming from the west and therefore the amount of rainfall received is high in the west and it reduces towards the east.

Question 5.
Why is rainfall more only in the eastern coast of Australia?
Answer:
The eastern part of Australia is a mountainous region. The winds blowing from the Pacific Ocean are obstructed by these mountains resulting in orographic rainfall towards the east and the formation of a rain shadow zone towards the west.

Observe the horizontal profile of Maharashtra in the following figure and answer the following questions:

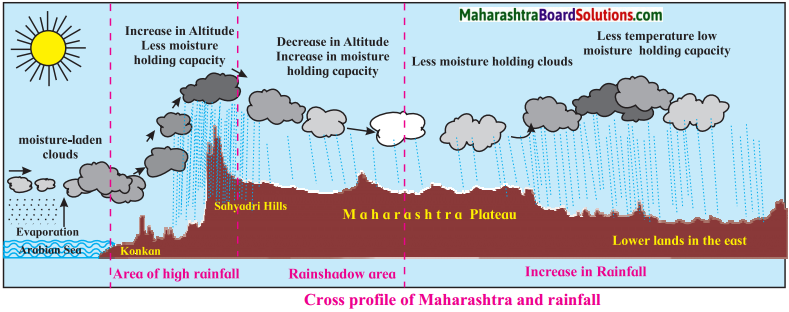
Question 1.
What type of rainfall occurs in Maharashtra?
Answer:
Orographic rainfall occurs in Maharashtra.

Question 2.
Where will the rain shadow area lie in Maharashtra?
Answer:
The rain shadow area lies to the Leeward side of Sahyadri hills (Maharashtra plateau).

Question 3.
Think about the figure and estimate the rainfall of your district.
Answer:
The answer may vary.

Give reasons:

Question 1.
Crops may get destroyed due to hailstones.
Answer:

• As hailstones are heavy they fall towards the earth’s surface, but because of the frequent upward flow of air, they are repeatedly taken upwards.
• Here, a new layer of snow encapsulates the hail. This happens quite a few times.
• Hence, concentric layers are formed while the hail grows in size.
• These big heavy hailstones fall rapidly to the ground because of gravity. This type of precipitation is called as hail.
• Hence due to hail, crops may get destroyed.

Question 2.
There is a difference between ice and snow.
Answer:

• In areas located at higher altitudes and high- latitudes, where the temperatures are below 0°C get precipitation in the form of snow.
• Snow is friable and opaque. This snow accumulates in the form of layers on top of each other.
• Because of the pressure from the upper layers, the lower layers of the snow become homogeneous, massive and transparent.
• Massive transparent snow formed in such a way is called ice.

Thus, there is a difference between ice and snow.

Question 3.
In equatorial areas, convectional rainfall occurs almost daily in the afternoons.
Answer:

• In equatorial areas, the surface gets heated because of the sun’s heat and the air near it also gets heated.
• As it gets heated, it spreads and becomes lighter and moves upwards. It cools down when it goes upward. The moisture-holding capacity of cold air is less.
• Consequently, condensation of the water vapour occurs and rainfall occurs in equatorial areas.
• Thus in equatorial areas, convectional rainfall occurs almost daily in the afternoons.

Question 4.
A rain shadow area is formed on the leeward side of the Western Ghats.
Answer:

• Winds coming from Arabian sea are moisture-laden. They are obstructed by the Western Ghats coming in their way.
• According to the slope of the Western Ghats, the moisture-laden winds start going upwards.
• The temperature of these winds drop and condensation occurs and rainfall takes place. Thus, because of the obstruction of the Western Ghats, orographic rainfall occurs.
• The windward side of the mountains gets more rain; amount of vapour in the air reduces after crossing the mountain and the water vapour carrying capacity of the air increases.
• The leeward side of the mountain gets lesser rainfall and hence a rain-shadow area is formed here.

Question 5.
Snowfall is not experienced in Maharashtra.
Answer:

• Solid snow particles are formed in regions where the temperature falls below the freezing point leading to the process of sublimation.
• In the sublimation process, the water vapour directly turns into snowflakes.
• In Maharashtra, during winters the temperature never falls below the freezing point.
• Hence snowflakes are never formed in the atmosphere.
• Thus snowfall is not experienced in Maharashtra.

Question 6.
Hailstones do not occur frequently.
Answer:

• Strong vertical movements of air with very high difference in temperature are an ideal condition for the formation of hailstones.
• Presence of moisture is also necessary in the air.
• Such conditions do not exist frequently.
• Hence hailstones are not experienced frequently.

Question 7.
Dew and frost occur on a large scale in winters.
Answer:

• During winters when moisture-laden air near the earth’s surface comes in contact very cold objects, condensation of the vapour takes place.
• They turn into very small water droplets. These water droplets get stick to the surface of the cold objects. This is called dew.
• If the temperature of the air is less than 0°C, the water droplets stuck to the surfaces of cold objects freeze.
• This frozen water droplet is called frost.
• Thus dew and frost occur on a large scale in winters.

Draw diagram of Rain Gauge:
Answer:

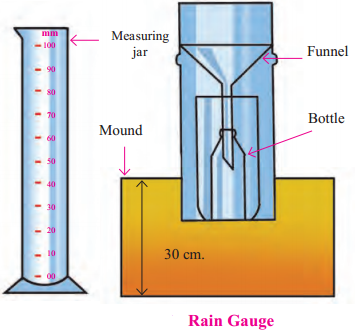
Question 6.
Explain the effects of precipitation.
Answer:

• The main source of potable water available on the earth is precipitation.
• As extreme rainfall is destructive so is the absence of rainfall.
• Floods may occur because of heavy rainfall and causes loss to life and property.
• If precipitation does not take place then conditions of drought arise. It causes a shortage of food and food may have to be imported and farmers’ conditions becomes grave.
• The economy of an agrarian1 country like India is dependent on agriculture. The agriculture in India to a large extent is dependent on monsoons. Hence rainfall in India is important to the whole country.
• A good rainfall at the right time increases crop production while untimely rain can damage the crope.
• Acid rains which is a combination of harmful gases and rainwater is harmful to the living organisms as well as non-living objects.

Explain:

Question 1.
Snowfall
Answer:

• When the temperature in the atmosphere falls below the freezing point, the water vapour directly turns into snowflakes. This is called sublimation.
• Here, the vapour in the form of gas transforms into solid snow.
• Precipitation in the form of solid particles is known as snowfall.
• In high latitudinal and temperate regions, snowfall occurs at the mean sea level while in tropical areas, snowfall occurs at places located higher than the snowline altitude.

Question 2.
Formation of hailstones.
Answer:

• When there is a lot of heat on the earth’s surface, the upward air flow blows at a great speed.
• Because of this upward flow, the temperature of the air reduces and the condensation of the water vapour takes place.
• Dark clouds are formed. Because of the upward movement of air, these water droplets go at a higher altitude.
• Here, solidification of these droplets occur and hailstones are formed.

Question 3.
Cyclonic rainfall
Answer:

• Cyclone is the specific air formation when the pressure at an area is less than the surrounding regions.
• Air from the surrounding region comes toward the center of the cyclone and starts moving upwards.
• As it rises, the temperature of the air reduces, condensation occurs and rainfall takes place.
• It rains in areas over which the cyclone passes. Cyclonic rainfall occurs more in temperate zones and its area is also quite extensive.
• Comparatively, cyclonic rainfall occurring in tropical regions is limited in extent and is stormy in nature.

Question 4.
Rain Gauge.
Answer:

• The instrument that is used to measure rainfall is called rain gauge.
• The funnel that is used for measuring rain has a specific diameter. The rain falling in this funnel is collected in a bottle fitted in the gauge.
• The collected water is then measured with the help of measuring jar. The measuring jar reads in millimetres.
• In areas of heavy rainfall, the reading of the rain is taken every three hours.
• The gauge is kept on open ground on a 30cm flat-mount. Hence, the rainwater is collected without any obstruction.

Question 5
Fog, dew and frost
Answer:
(i) Fog:

• The temperature of the layers of the air near the surface of the earth reduces. As temperature reduces, water vapour condenses.
• In this process, vapour turns into microscopic water particles and float in the air.
• When the density of these droplets in the air increases, fog occurs.

(ii) Dew:

• When moisture-laden air near the earth’s surface comes in contact with very cold objects, condensation of the vapour takes place. They turn into very small water droplets.
• These water droplets get stick to the surface of the cold objects. This is called dew.

(iii) Frost:

• If the temperature of the air reaches less than 0°C, the water droplets stuck to the surfaces of cold objects and freeze.
• This frozen water droplet is called frost.

Question 6.
Acid Rain
Answer:

• Because of air pollution in industrial areas, various gases get mixed in the air.
• Different adds are created when the water vapour in the air reacts chemically with these gases. For example, nitric add, sulphuric add, etc.
• Acids dissolved in rainwater fall with the rain j during precipitation. Such a type of rain which has acids dissolved in it is called acid rain.
• Such type of rainfall is harmful to the living organisms and the non-living objects.

Question 7.
Convectional Rainfall
Answer:

1. In equatorial areas, the surface gets heated because of the sun’s heat and the air near it also gets heated. As it gets heated, it spreads and becomes lighter and moves upwards.
2. It cools down when it goes upward & as the j moisture-holding capacity of cold air is less, condensation and rainfall occurs.
3. This type of rainfall is called as Convectional! Rainfall.
4. In equatorial areas, such a type of rainfall occurs almost daily in the afternoons. Rainfall is accompanied by lightning and thunder.
5. The Congo basin of the Africa and the Amazon basin in the South America experience convectional rainfall.
6. Such a rainfall has a very limited area on the earth.

Question 8.
Orographic rainfall
Answer:

• Winds coming from lakes or seas are moisture-laden. They are obstructed by the high mountain ranges coming in their way.
• They start going upwards along the slope of the mountains.
• The temperature of these winds drop and condensation occurs and rainfall takes place. Thus because of the obstruction of the mountains, this type of rainfall occurs.
• The windward side of the mountains gets; more rain; the amount of vapour in the air reduces after crossing the mountain and the moisture-holding capacity of the air increases.
• The leeward side of the mountain gets lesser rainfall and hence this area is identified as rain- shadow area.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 4 Operations on Fractions Class 6 Practice Set 9 Answers Solutions.

6th Standard Maths Practice Set 9 Answers Chapter 4 Operations on Fractions

Question 1.
Convert into improper fractions:
i. \(7 \frac{2}{5}\)
ii. \(5 \frac{1}{6}\)
iii. \(4 \frac{3}{4}\)
iv. \(2 \frac{5}{9}\)
v. \(1 \frac{5}{7}\)
Solution:
i. \(7 \frac{2}{5}\)

ii. \(5 \frac{1}{6}\)

iii. \(4 \frac{3}{4}\)

iv. \(2 \frac{5}{9}\)

v. \(1 \frac{5}{7}\)

Question 2.
Convert into mixed numbers:
i. \(\frac { 30 }{ 7 }\)
ii. \(\frac { 7 }{ 4 }\)
iii. \(\frac { 15 }{ 12 }\)
iv. \(\frac { 11 }{ 8 }\)
v. \(\frac { 21 }{ 4 }\)
v. \(\frac { 20 }{ 7 }\)
Solution:
i. \(\frac { 30 }{ 7 }\)

ii. \(\frac { 7 }{ 4 }\)

iii. \(\frac { 15 }{ 12 }\)

iv. \(\frac { 11 }{ 8 }\)

v. \(\frac { 21 }{ 4 }\)

v. \(\frac { 20 }{ 7 }\)

Question 3.
Write the following examples using fraction:
i. If 9 kg rice is shared among 5 people, how many kilograms of rice does each person get?
ii. To make 5 shirts of the same size, 11 meters of cloth is needed. How much cloth is needed for one shirt?
Solution:
i. Total quantity of rice = 9 kg
Number of people = 5
∴ Kilograms of rice received by each person = \(\frac { 9 }{ 5 }\)
∴ Each person will get \(\frac { 9 }{ 5 }\) kg of rice.

ii. Total meters of cloth = 11 meters
Number of shirts to be made = 5
Meters of cloth needed to make 1 shirt = \(\frac { 11 }{ 5 }\)
∴ Cloth needed to make 1 shirt is \(\frac { 11 }{ 5 }\) meters.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.3 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 5 Probability.

Practice Set 5.3 Algebra 10th Std Maths Part 1 Answers Chapter 5 Probability

Question 1.
Write sample space ‘S’ and number of sample points n(S) for each of the following experiments. Also write events A, B, C in the set form and write n(A), n(B), n(C).

i. One die is rolled,
Event A: Even number on the upper face.
Event B: Odd number on the upper face.
Event C: Prime number on the upper face.

ii. Two dice are rolled simultaneously,
Event A: The sum of the digits on upper faces is a multiple of 6.
Event B: The sum of the digits on the upper faces is minimum 10.
Event C: The same digit on both the upper faces.

iii. Three coins are tossed simultaneously.
Condition for event A: To get at least two heads.
Condition for event B: To get no head.
Condition for event C: To get head on the second coin.

iv. Two digit numbers are formed using digits 0, 1, 2, 3, 4, 5 without repetition of the digits.
Condition for event A: The number formed is even.
Condition for event B: The number is divisible by 3.
Condition for event C: The number formed is greater than 50.

v. From three men and two women, environment committee of two persons is to be formed.
Condition for event A: There must be at least one woman member.
Condition for event B: One man, one woman committee to be formed.
Condition for event C: There should not be a woman member.

vi. One coin and one die are thrown simultaneously.
Condition for event A: To get head and an odd number.
Condition for event B: To get a head or tail and an even number.
Condition for event C: Number on the upper face is greater than 7 and tail on the coin.
Solution:
i. Sample space (S) = {1, 2, 3, 4, 5, 6}
∴ n(S) = 6
Condition for event A: Even number on the upper face.
∴ A = {2,4,6}
∴ n(A) = 3
Condition for event B: Odd number on the upper face.
∴ B = {1, 3, 5}
∴ n(B) = 3
Condition for event C: Prime number on the upper face.
∴ C = {2, 3, 5}
∴ n(C) = 3

ii. Sample space,
S = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}
∴ n(S) = 36
Condition for event A: The sum of the digits on the upper faces is a multiple of 6.
A = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (6, 6)}
∴ n(A) = 6

Condition for event B: The sum of the digits on the upper faces is minimum 10.
B = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}
∴ n(B) = 6

Condition for event C: The same digit on both the upper faces.
C = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
∴ n(C) = 6

iii. Sample space,
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
∴ n(S) = 8

Condition for event A: To get at least two heads.
∴ A = {HHT, HTH, THH, HHH}
∴ n(A) = 4

Condition for event B: To get no head.
∴ B = {TTT}
∴ n(B) = 1

Condition for event C: To get head on the second coin.
∴ C = {HHH, HHT, THH, THT}
∴ n(C) = 4

iv. Sample space (S) = {10, 12, 13, 14, 15,
20, 21, 23, 24, 25,
30, 31, 32, 34, 35,
40, 41, 42, 43,
45, 50, 51, 52, 53, 54}
∴ n(S) = 25
Condition for event A: The number formed is even
∴ A = {10, 12, 14, 20, 24, 30, 32, 34, 40, 42, 50, 52, 54)
∴ n(A) = 13
Condition for event B: The number formed is divisible by 3.
∴ B = {12, 15, 21, 24, 30, 42, 45, 51, 54}
∴ n(B) = 9
Condition for event C: The number formed is greater than 50.
∴ C = {51,52, 53,54}
∴ n(C) = 4

v. Let the three men be M₁, M₂, M₃ and the two women be W₁, W₂.
Out of these men and women, a environment committee of two persons is to be formed.
∴ Sample space,
S = {M₁M₂, M₁M₃, M₁W₁, M₁W₂, M₂M₃, M₂W₁, M₂W₂, M₃W₁, M₃W₂, W₁W₂}
∴ n(S) = 10
Condition for event A: There must be at least one woman member.
∴ A = {M₁W₁, M₁W₂, M₂W₁, M₂W₂, M₃W₁, M₃W₂, W₁W₂}
∴ n(A) = 7
Condition for event B: One man, one woman committee to be formed.
∴ B = {M₁W₁, M₁W₂, M₂W₁, M₂W₂, M₃W₂, M₃W₂}
∴ n(B) = 6
Condition for event C: There should not be a woman member.
∴ C = {M₁M₂, M₁M₃, M₂M₃}
∴ n(C) = 3

vi. Sample space,
S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
∴ n(S) = 12
Condition for event A: To get head and an odd number.
∴ A = {(H, 1), (H, 3), (H, 5)}
∴ n(A) = 3
Condition for event B: To get a head or tail and an even number.
∴ B = {(H, 2), (H, 4), (H, 6), (T, 2), (T, 4), (T, 6)}
∴ n(B) = 6
Condition for event C: Number on the upper face is greater than 7 and tail on the coin.
The greatest number on the upper face of a die is 6.
∴ Event C is an impossible event.
∴ C = { }
∴ n(C) = 0

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 40 Answers Solutions Chapter 10 Bank and Simple Interest.

Bank and Simple Interest Class 7 Practice Set 40 Answers Solutions Chapter 10

Question 1.
If Rihanna deposits Rs 1500 in the school fund at 9 p.c.p.a for 2 years, what is the total amount she will get?
Solution:
Here, P = Rs 1500, R = 9 p.c.p.a , T = 2 years
∴ Total interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{1500 \times 9 \times 2}{100}\)
= 1500 x 9 x 2
= Rs 270
∴ Total amount = Principal + Interest
= 1500 + 270
= Rs 1770
∴ Rihanna will get a total amount of Rs 1770.

Question 2.
Jethalal took a housing loan of Rs 2,50,000 from a bank at 10 p.c.p.a. for 5 years. What is the yearly interest he must pay and the total amount he returns to the bank?
Solution:
Here, P = Rs 250000, R = 10 p.c.p.a., T = 5 years
∴ Total interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{250000 \times 10 \times 5}{100}\)
= 2500 x 10 x 5
= Rs 1,25,000
∴ Yearly interest = Total interest ÷ Time = 1,25,000 ÷ 5 = Rs 25000
Total amount to be returned = Principal + Total interest
= 250000 + 125000 = Rs 375000
∴ The yearly interest is Rs 25,000 and Jethalal will have to return Rs 3,75,000 to the bank.

Question 3.
Shrikant deposited Rs 85,000 for \(2\frac { 1 }{ 2 }\) years at 7 p.c.p.a. in a savings bank account. What is the total
interest he received at the end of the period?
Solution:
Here, P = Rs 85000, R = 7 p.c.p.a., T = \(2\frac { 1 }{ 2 }\) years = 2.5 years
∴ Total interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{85000 \times 7 \times 2.5}{100}\)
= \(\frac{85000 \times 7 \times 25}{100 \times 10}\)
= 85 x 7 x 25
= Rs 14875
∴ The total interest received by Shrikant at the end of the period is Rs 14875.

Question 4.
At a certain rate of interest, the interest after 4 years on Rs 5000 principal is Rs 1200. What would be the interest on Rs 15000 at the same rate of interest for the same period?
Solution:
The interest on Rs 5000 after 4 years is Rs 1200.
Let us suppose the interest on Rs 15000 at the same rate after 4 years is Rs x.
Taking the ratio of interest and principal, we get
∴ \(\frac{x}{15000}=\frac{1200}{5000}\)
∴ \(x=\frac{1200 \times 15000}{5000}\)
= Rs 3600
∴ The interest received on Rs 15000 is Rs 3600.

Question 5.
If Pankaj deposits Rs 1,50,000 in a bank at 10 p.c.p.a. for two years, what is the total amount he will get from the bank?
Solution:
Here, P = 150000, R = 10 p.c.p.a., T = 2 years
∴ Total interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{150000 \times 10 \times 2}{100}\)
= Rs 30000
∴ Total amount = Principal + Total Interest
= 150000 + 30000
= Rs 180000
∴ Pankaj will receive Rs 180000 from the bank.

Maharashtra Board Class 7 Maths Chapter 10 Banks and Simple Interest Practice Set 40 Intext Questions and Activities

Question 1.
Observe the entries made in the page of a passbook shown below and answer the following questions. (Textbook pg. no. 70)

1. On 2.2.16 the amount deposited was Rs__and the balance Rs__.
2. On 12.2.16, Rs__were withdrawn by cheque no. 243965. The balance was Rs__
3. On 26.2.2016 the bank paid an interest of Rs__

Solution:

1. 1500, 7000
2. 3000, 9000
3. 135

Practice Set 40 Class 7 Question 2.
Suvidya borrowed a sum of Rs 30000 at 8 p.c.p.a. interest for a year from her bank to buy a computer. At the end of the period, she had to pay back an amount of Rs 2400 over and above what she had borrowed.
Based on this information fill in the blanks below. (Textbook pg. no. 70)

1. Principal = Rs__
2. Rate of interest =__%
3. Interest = Rs__
4. Time =__year.
5. The total amount returned to the bank = 30,000 + 2,400 = Rs__

Solution:

1. 30000
2. 8
3. 2400
4. 1
5. Rs 32400

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 16 Quadrilaterals Class 6 Practice Set 37 Answers Solutions.

6th Standard Maths Practice Set 37 Answers Chapter 16 Quadrilaterals

Question 1.
Observe the figures below and find out their names:

Solution:
i. Pentagon (5 sides)
ii. Hexagon (6 sides)
iii. Heptagon (7 sides)
iv. Octagon (8 sides)

Maharashtra Board Class 6 Maths Chapter 16 Quadrilaterals Practice Set 37 Intext Questions and Activities

Question 1.
Observe the figures given below and say which of them are quadrilaterals. (Textbook pg. no. 81)

Solution:
Is a quadrilateral: (i)

Question 2.
Draw a quadrilateral. Draw one diagonal of this quadrilateral and divided it into two triangles. Measures all the angles in the figure. Is the sum of the measures of the four angles of the quadrilateral equal to the sum of the measures of the six angles of the two triangles? Verity that this is so with other quadrilaterals. (Textbook pg. no. 84)
Solution:

m∠PQR = 104°
m∠QRP = 26°
m∠RPQ = 50°
m∠PRS = 34°
m∠RSP = 106°
m∠SPR = 40°
∴ Sum of the measures of the angles of quadrilateral = m∠PQR + m∠QRP + m∠RPQ + m∠PRS + m∠RSP + m∠SPR
= 104° + 26° + 50° + 34° + 106° + 40°
= 360°
Also, we observe that
Sum of the measures of the angles of quadrilateral = Sum of the measures of angles of the two triangles (PQR and PRS)
= (104°+ 26°+ 50°)+ (34° + 106° + 40°)
= 180° + 180°
= 360°
[Note: Students should drew different quadrilaterals and verify the property.]

Question 3.
For the pentagon shown in the figure below, answer the following: (Textbook pg. no. 84)

1. Write the names of the five vertices of the pentagon.
2. Name the sides of the pentagon.
3. Name the angles of the pentagon.
4. See if you can sometimes find players on a field forming a pentagon.

Solution:

1. The vertices of the pentagon are points A, B, C, D and E.
2. The sides of the pentagon are segments AB, BC, CD, DE and EA.
3. The angles of the pentagon are ∠ABC, ∠BCD, ∠CDE, ∠DEA and ∠EAB.
4. The players shown in the above figure form a pentagon. The players are standing on the vertices of

Question 4.
Cut out a paper in the shape of a quadrilateral. Make folds in it that join the vertices of opposite angles. What can these folds be called? (Textbook pg. no. 83)

Solution:
The folds are called diagonals of the quadrilateral.

Question 5.
Take two triangular pieces of paper such that . one side of one triangle is equal to one side of the other. Let us suppose that in ∆ABC and ∆PQR, sides AC and PQ are the equal sides. Join the triangles so that their equal sides lie B side by side. What figure do we get? (Textbook pg. no. 83)

Solution:
If we place the triangles together such that the equal sides overlap, the two triangles form a quadrilateral.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 13 Profit-Loss Class 6 Practice Set 33 Answers Solutions.

6th Standard Maths Practice Set 33 Answers Chapter 13 Profit-Loss

Question 1.
Maganlal bought trousers for Rs 400 and a shirt for Rs 200 and sold them for Rs 448 and Rs 250 respectively. Which of these transactions was more profitable?
Solution:
Cost price of trousers = Rs 400
Selling price of trousers = Rs 448
Profit = Selling price – Cost price
= 448 – 400 = Rs 48
Let Maganlal make x % profit on selling trousers

∴ x = 12%
Cost price of shirt = Rs 200
Selling price of shirt = Rs 250
∴ Profit = Selling price – Cost price
= 250 – 200
= Rs 50
Let Maganlal make y% profit on selling shirt.

∴ y = 25%
∴ Transaction involving selling of shirt was more profitable.

Question 2.
Ramrao bought a cupboard for Rs 4500 and sold it for Rs 4950. Shamrao bought a sewing machine for Rs 3500 and sold it for Rs 3920. Whose transaction was more profitable?
Solution:
Cost price of cupboard = Rs 4500
Selling price of cupboard = Rs 4950
∴ Profit = Selling price – Cost price
= 4950 – 4500
= Rs 450
Let Ramrao make x% profit on selling cupboard

∴ x = 10%
Cost price of sewing machine = Rs 3500
Selling price of sewing machine = Rs 3920
∴Profit = Selling price – Cost price
= 3920 – 3500
= Rs 420
Shamrao make y% profit on selling sewing machine.

∴y = 12%
∴Shamrao’s transaction was more profitable.

Question 3.
Hanif bought one box of 50 apples for Rs 400. He sold all the apples at the rate of Rs 10 each. Was there a profit or loss? What was its percentage?
Solution:
Cost price of 50 apples = Rs 400
Selling price of one apple = Rs 10
∴ Selling price of 50 apples = 10 x 50 = Rs 500
Selling price is greater than the total cost price.
∴ Hanif made a profit.
∴ Profit = Selling price – Cost price
= 500 – 400
= Rs 100
Let Hanif make of x% profit on selling apples.

∴ x = 25%
∴ Hanif made a profit of 25%.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 9 HCF-LCM Class 6 Practice Set 24 Answers Solutions.

6th Standard Maths Practice Set 24 Answers Chapter 9 HCF-LCM

Question 1.
Find the HCF of the following numbers.
i. 45, 30
ii. 16, 48
iii. 39, 25
iv. 49, 56
v. 120, 144
vi. 81, 99
vii. 24, 36
viii. 25, 75
ix. 48, 54
x. 150, 225
Solution:
i. Factors of 45 = 1, 3, 5, 9,15, 45
Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30
∴ HCF of 45 and 30 = 15

ii. Factors of 16 = 1, 2, 4, 8, 16
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
∴ HCF of 16 and 48 = 16

iii. Factors of 39 = 1, 3, 13, 39
Factors of 25 = 1, 5, 25
∴ HCF of 39 and 25 = 1

iv. Factors of 49 = 1, 7, 49
Factors of 56 = 1, 2, 4, 7, 8, 14, 28, 56
∴ HCF of 49 and 56 = 7

v. Factors of 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Factors of 144 = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144
∴ HCF of 120 and 144 = 24

vi. Factors of 81 = 1, 3, 9, 27, 81
Factors of 99 = 1, 3, 9, 11, 33, 99
∴ HCF of 81 and 99 = 9

vii. Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
∴ HCF of 24 and 36 = 12

viii. Factors of 25 = 1, 5, 25
Factors of 75 = 1, 3, 5, 15, 25, 75
∴ HCF of 25 and 75 = 25

ix. Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Factors of 54 = 1, 2, 3, 6, 9, 18, 27, 54
∴ HCF of 48 and 54 = 6

x. Factors of 150 = 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
Factors of 225 = 1, 3, 5, 9, 15, 25, 45, 75, 225
∴ HCF of 150 and 225 = 75

Question 2.
If large square beds of equal size are to be made for planting vegetables on a plot of land 18 metres long and 15 metres wide, what is the maximum possible length of each bed?
Solution:
Length of the land = 18 m
Width of the land = 15 m
The maximum length of each bed will be the greatest common factor of 18 and 15.
Factors of 18 = 1, 2, 3, 6, 9, 18
Factors of 15 = 1, 3, 5, 15
∴ HCF of 18 and 15 = 3
∴ The maximum possible length of each bed is 3 metres.

Question 3.
Two ropes, one 8 metres long and the other 12 metres long are to be cut into pieces of the same length. What will the maximum possible length of each piece be?
Solution:
Length of first rope = 8 m
Length of second rope = 12 m
The maximum length of each piece will be the greatest common factor of 8 and 12.
Factors of 8 = 1, 2, 4, 8
Factors of 12 = 1, 2, 3, 4, 6, 12
∴ HCF of 8 and 12 = 4
∴ The maximum possible length of each piece is 4 metres.

Question 4.
The number of students of Std 6th and Std 7th who went to visit the Tadoba Tiger Project at Chandrapur was 140 and 196 respectively. The students of each class are to be divided into groups of the same number of students. Each group can have a paid guide. What is the maximum number of students that can be there in each group? Why do you think each group should have the maximum possible number of students?
Solution:
Number of students of Std 6th = 140
Number of students of Std 7th = 196
The maximum number of students in each group will be the greatest common factor of 140 and 196.
Factors of 140 = 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
Factors of 196 = 1, 2, 4, 7, 14, 28, 49, 98, 196
∴ HCF of 140 and 196 = 28
∴ Maximum students in each group are 28.
Each group should have maximum number students so that there will be minimum number of groups and hence minimum number of paid guides.

Question 5.
At the Rice Research Centre at Tumsar there are 2610 kg of seeds of the basmati variety and 1980 kg of the indrayani variety. If the maximum possible weight of seeds has to be filled to make bags of equal weight what would be the weight of each bag? How many bags of each variety will there be?
Solution:
Weight of basmati rice = 2610 kg
Weight of indrayani rice = 1980 kg
The weight of each bag will be the greatest common factor of 2610 and 1980.
Factors of 2610 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 29, 30, 45, 58, 87, 90, 145, 174, 261, 290, 435, 522, 870, 1305, 2610
Factors of 1980 = 1, 2, 3, 4, 5, 6, 9, 10, 11, 12, 15, 18, 20, 22, 30, 33, 36, 44, 45, 55, 60, 66, 90, 99, 110, 132, 165, 180, 198, 220, 330, 396, 495, 660, 990, 1980
∴ HCF of 2610 and 1980 = 90
Maximum weight of each bag = 90 kg
Number of bags of basmati rice = 2610 ÷ 90 = 29
Number of bags of indrayani rice = 1980 ÷ 90 = 22
Maximum weight of each bag is 90 kg.
The number of bags of basmati rice is 29, and the number of bags of indrayani rice is 22.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 11.2 8th Std Maths Answers Solutions Chapter 11 Statistics.

Practice Set 11.2 8th Std Maths Answers Chapter 11 Statistics

practice set 11.2 8th class Question 1.
Observe the following graph and answer the questions.

i. State the type of the graph.
ii. How much is the savings of Vaishali in the month of April?
iii. How much is the total of savings of Saroj in the months March and April?
iv. How much more is the total savings of Savita than the total savings of Megha?
v. Whose savings in the month of April is the least?
Solution:
i. The given graph is a subdivided bar graph.
ii. Vaishali’s savings in the month of April is Rs 600.
iii. Total savings of Saroj in the months of March and April is Rs 800.
iv. Savita’s total saving = Rs 1000, Megha’s total saving = Rs 500
∴ difference in their savings = 1000 – 500 = Rs 500.
Savita’s saving is Rs 500 more than Megha.
v. Megha’s savings in the month of April is the least.

practice set 11.2 Question 2.
The number of boys and girls, in std 5 to std 8 in a Z.P. School is given in the table. Draw a subdivided bar graph to show the data. (Scale : On Y axis, 1cm = 10 students)

Standard	5th	6th	7th	8th
Boys	34	26	21	25
Girls	17	14	14	20

Solution:

Standard	5th	6th	7th	8th
Boys	34	26	21	25
Girls	17	14	14	20
Total	51	40	35	45

Statistics class 8 practice set 11.1 Question 3.
In the following table number of trees planted in the year 2016 and 2017 in four towns is given. Show the data with the help of subdivided bar graph.

Year\Town	karjat	Wadgaon	Shivapur	Khandala
2016	150	250	200	100
2017	200	300	250	150

Solution:

Year\Town	karjat	Wadgaon	Shivapur	Khandala
2016	150	250	200	100
2017	200	300	250	150
Total	350	550	450	250

Statistics class 8 Question 4.
In the following table, data of the transport means used by students in 8th standard for commutation between home and school is given. Draw a subdivided bar diagram to show the data.
(Scale: On Y axis: 1 cm = 500 students)

Means of commutation\Town	Paithan	Yeola	Shahapur
Cycle	3250	1500	1250
Bus and auto	750	500	500
On foot	1000	1000	500

Solution:

Means of commutation\Town	Paithan	Yeola	Shahapur
Cycle	3250	1500	1250
Bus and auto	750	500	500
On foot	1000	1000	500
Total	5000	3000	2250

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.5 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

Practice Set 4.5 Algebra 9th Std Maths Part 1 Answers Chapter 4 Ratio and Proportion

Question 1.
Which number should be subtracted from 12, 16 and 21 so that resultant numbers are in continued proportion?
Solution:
Let the number to be subtracted be x.
∴ (12 – x), (16 – x) and (21 – x) are in continued proportion.

∴ 84 – 4x = 80 – 5x
∴ 5x – 4x = 80 – 84
∴ x = -4
∴ -4 should be subtracted from 12,16 and 21 so that the resultant numbers in continued proportion.

Question 2.
If (28 – x) is the mean proportional of (23 – x) and (19 – x), then find the value ofx.
Solution:
(28 – x) is the mean proportional of (23 – x) and (19-x). …[Given]

∴ -5(19 – x) = 9(28 – x)
∴ -95 + 5x = 252 – 9x
∴ 5x + 9x = 252 + 95
∴ 14x = 347
∴ x = \(\frac { 347 }{ 14 }\)

Question 3.
Three numbers are in continued proportion, whose mean proportional is 12 and the sum of the remaining two numbers is 26, then find these numbers.
Solution:
Let the first number be x.
∴ Third number = 26 – x
12 is the mean proportional of x and (26 – x).
∴ \(\frac { x }{ 12 }\) = \(\frac { 12 }{ 26 – x }\)
∴ x(26 – x) = 12 x 12
∴ 26x – x² = 144
∴ x² – 26x + 144 = 0
∴ x² – 18x – 8x + 144 = 0
∴ x(x – 18) – 8(x – 18) = 0
∴ (x – 18) (x – 8) = 0
∴ x = 18 or x = 8
∴ Third number = 26 – x = 26 – 18 = 8 or 26 – x = 26 – 8 = 18
∴ The numbers are 18, 12, 8 or 8, 12, 18.

Question 4.
If (a + b + c)(a – b + c) = a² + b² + c², show that a, b, c are in continued proportion.
Solution:
(a + b + c)(a – b + c) = a² + b² + c² …[Given]
∴ a(a – b + c) + b(a – b + c) + c(a – b + c) = a2 + b2 + c2
∴ a² – ab + ac + ab – b² + be + ac – be + c² = a² + b² + c²
∴ a² + 2ac – b² + c² = a² + b² + c²
∴ 2ac – b² = b²
∴ 2ac = 2b²
∴ ac = b²
∴ b² = ac
∴ a, b, c are in continued proportion.

Question 5.
If \(\frac { a }{ b }\) = \(\frac { b }{ c }\) and a, b, c > 0, then show that,
i. (a + b + c)(b – c) = ab – c²
ii. (a² + b²)(b² + c²) = (ab + be)²
iii. \(\frac{a^{2}+b^{2}}{a b}=\frac{a+c}{b}\)
Solution:
Let \(\frac { a }{ b }\) = \(\frac { b }{ c }\) = k
∴ b = ck
∴ a = bk =(ck)k
∴ a = ck² …(ii)

i. (a + b + c)(b – c) = ab – c²
L.H.S = (a + b + c) (b – c)
= [ck² + ck + c] [ck – c] … [From (i) and (ii)]
= c(k² + k + 1) c (k – 1)
= c² (k² + k + 1) (k – 1)
R.H.S = ab – c²
= (ck²) (ck) – c² … [From (i) and (ii)]
= c²k³ – c²
= c²(k³ – 1)
= c² (k – 1) (k² + k + 1) … [a³ – b³ = (a – b) (a² + ab + b²]
∴ L.H.S = R.H.S
∴ (a + b + c) (b – c) = ab – c²

ii. (a² + b²)(b² + c²) = (ab + bc)²
b = ck; a = ck²
L.H.S = (a² + b²) (b² + c²)
= [(ck²) + (ck)²] [(ck)² + c²] … [From (i) and (ii)]
= [c²k⁴ + c²k²] [c²k² + c²]
= c²k² (k² + 1) c² (k² + 1)
= c4k² (k² + 1)²
R.H.S = (ab + bc)²
= [(ck²) (ck) + (ck)c]² …[From (i) and (ii)]
= [c²k³ + c²k]²
= [c²k (k² + 1)]2 = c⁴(k² + 1)²
∴ L.H.S = R.H.S
∴ (a² + b²) (b² + c²) = (ab + bc)²

iii. \(\frac{a^{2}+b^{2}}{a b}=\frac{a+c}{b}\)

9th Standard Algebra Practice Set 4.5 Question 6. Find mean proportional of \(\frac{x+y}{x-y}, \frac{x^{2}-y^{2}}{x^{2} y^{2}}\).
Solution:
Let a be the mean proportional of \(\frac{x+y}{x-y}\) and \(\frac{x^{2}-y^{2}}{x^{2} y^{2}}\)

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Miscellaneous Problems Set 1 Answers Solutions.

Maharashtra Board Miscellaneous Problems Set 1 Class 7 Maths Solutions

Question 1.
Solve the following:
i. (-16) × (-5)
ii. (72) ÷ (-12)
iii. (-24) × (2)
iv. 125 ÷ 5
v. (-104) ÷ (-13)
vi. 25 × (-4)
Solution:
i. (-16) × (-5) = 80

ii. 72 ÷ (-12) = \(\frac { 72 }{ -12 }\)
= \(\frac{1}{(-1)} \times \frac{72}{12}\)
(-1) × 12
= -6

iii. (-24) × 2 = -48

iv. 125 ÷ 5 = \(\frac { 125 }{ 5 }\)
= 25

v. (-104) ÷ (-13) = \(\frac { -104 }{ -13 }\)
= \(\frac { 104 }{ 13 }\)
= 8

vi. 25 × (-4) = -100

Question 2.
Find the prime factors of the following numbers and find their LCM and HCF:
i. 75,135
ii. 114,76
iii. 153,187
iv. 32,24,48
Solution:
i. 75 = 3 × 25
= 3 × 5 × 5
135 = 3 × 45
= 3 × 3 × 15
= 3 × 3 × 3 × 5
∴ HCF of 75 and 135 = 3 × 5
= 15
LCM of 75 and 135 = 3 × 5 × 5 × 3 × 3
= 675

ii. 114 = 2 × 57
= 2 × 3 × 19
76 = 2 × 38
= 2 × 2 × 19
∴ HCF of 114 and 76 = 2 × 19
= 38
LCM of 114 and 76 = 2 × 19 × 3 × 2
= 228

iii. 153 = 3 × 51
= 3 × 3 × 17
187 = 11 × 17
∴ HCF of 153 and 187 = 17
LCM of 153 and 187 = 17 × 3 × 3 × 11
= 1683

iv. 32 = 2 × 16
= 2 × 2 × 8
= 2 × 2 × 2 × 4
= 2 × 2 × 2 × 2 × 2
24 = 2 × 12
= 2 × 2 × 6
= 2 × 2 × 2 × 3
48 = 2 × 24
= 2 × 2 × 12
= 2 × 2 × 2 × 6
= 2 × 2 × 2 × 2 × 3
∴ HCF of 32, 24 and 48 = 2 × 2 × 2
= 8
LCM of 32,24 and 48 = 2 × 2 × 2 × 2 × 2 × 3
= 96

Question 3.
Simplify:
i. \(\frac { 322 }{ 391 }\)
ii. \(\frac { 247 }{ 209 }\)
iii. \(\frac { 117 }{ 156 }\)
Solution:
i. \(\frac { 322 }{ 391 }\)

ii. \(\frac { 247 }{ 209 }\)

iii. \(\frac { 117 }{ 156 }\)

Question 4.
i. 784
ii. 225
iii. 1296
iv. 2025
v. 256
Solution:
i. 784

∴ 784 = 2 × 2 × 2 × 2 × 7 × 7
∴ √784 = 2 × 2 × 7
= 28

ii. 225

∴ 225 = 3 × 3 × 5 × 5
∴ √225 = 3 × 5
= 15

iii. 1296

∴ 1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
∴ √1296 = 2 × 2 × 3 × 3
= 36

iv. 2025

∴ 2025 = 3 × 3 × 3 × 3 × 5 × 5
∴ √2025 = 3 × 3 × 5
= 45

v. 256

∴ 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ √256 = 2 × 2 × 2 × 2
= 16

Question 5.
There are four polling booths for a certain election. The numbers of men and women who cast their vote at each booth is given in the table below. Draw a joint bar graph for this data.

Polling Booths	Navodaya Vidyalaya	Vidyaniketan School	City High School	Eklavya School
Women	500	520	680	800
Men	440	640	760	600

Solution:

Question 6.
Simplify the expressions:
i. 45 ÷ 5 + 120 × 4 – 12
ii. (38 – 8) × 2 ÷ 5 + 13
iii. \(\frac{5}{3}+\frac{4}{7} \div \frac{32}{21}\)
iv. 3 × {4 [85 + 5 – (15 – 3)] + 2}
Solution:
i. 45 ÷ 5 + 120 × 4 – 12
= 9 + 80 – 12
= 89 – 12
= 77

ii. (38 – 8) × 2 ÷ 5 + 13
= 30 × 2 ÷ 5 + 13
= 60 ÷ 5 + 13
= 12 + 13
= 25

iii. \(\frac{5}{3}+\frac{4}{7} \div \frac{32}{21}\)
\(\frac{5}{3}+\frac{4}{7} \times \frac{21}{32}\)
\(\frac{5}{3}+\frac{3}{8}=\frac{40}{24}+\frac{9}{24}\)
\(\frac{49}{24}\)

iv. 3 × {4 [85 + 5 – (15 – 3)] + 2}
= 3 × {4[90 – 5] + 2}
= 3 × {4 × 85 + 2}
= 3 × (340 + 2)
= 3 × 342
= 1026

Question 7.
Solve:
i. \(\frac{5}{12}+\frac{7}{16}\)
ii. \(3 \frac{2}{5}-2 \frac{1}{4}\)
iii. \(\frac{12}{5} \times \frac{(-10)}{3}\)
iv. \(4 \frac{3}{8} \div \frac{25}{18}\)
Solution:
i. \(\frac{5}{12}+\frac{7}{16}\)

ii. \(3 \frac{2}{5}-2 \frac{1}{4}\)

iii. \(\frac{12}{5} \times \frac{(-10)}{3}\)
= 4 × (-2)
= -8

iv. \(4 \frac{3}{8} \div \frac{25}{18}\)
= \(\frac{7}{4} \times \frac{9}{5}\)
= \(\frac { 63 }{ 20 }\)

Question 8.
Construct ∆ABC such that m∠A = 55°, m∠B = and l(AB) = 5.9 cm.
Solution:

Question 9.
Construct ∆XYZ such that, l(XY) = 3.7 cm, l(YZ) = 7.7 cm, l(XZ) = 6.3 cm.
Solution:

Question 10.
Construct ∆PQR such that, m∠P = 80°, m∠Q = 70°, l(QR) = 5.7 cm.
Ans:
In ∆PQR,
m∠P + m∠Q + m∠R = 180° …. (Sum of the measures of the angles of a triangle is 180°)
∴ 80 + 70 + m∠R = 180
∴ 150 + m∠R = 180
∴ m∠R = 180 – 150
∴ m∠R = 30°

Question 11.
Construct ∆EFG from the given measures. l(FG) = 5 cm, m∠EFG = 90°, l(EG) = 7 cm.
Solution:

Question 12.
In ∆LMN, l(LM) = 6.2 cm, m∠LMN = 60°, l(MN) 4 cm. Construct ∆LMN.
Solution:

Question 13.
Find the measures of the complementary angles of the following angles:
i. 35°
ii. a°
iii. 22°
iv. (40 – x)°
Solution:
i. Let the measure of the complementary
angle be x°.
35 + x = 90
∴35 + x-35 = 90 – 35
….(Subtracting 35 from both sides)
∴x = 55
∴The complementary angle of 35° is 55°.

ii. Let the measure of the complementary angle be x°.
a + x = 90
∴a + x – a = 90 – a
….(Subtracting a from both sides)
∴x = (90 – a)
∴The complementary angle of a° is (90 – a)°.

iii. Let the measure of the complementary angle be x°.
22 + x = 90
∴22 + x – 22 = 90 – 22
….(Subtracting 22 from both sides)
∴x = 68
∴The complementary angle of 22° is 68°.

iv. Let the measure of the complementary angle be a°.
40 – x + a = 90
∴40 – x + a – 40 + x = 90 – 40 + x
….(Subtracting 40 and adding x on both sides)
∴a = (50 + x)
∴The complementary angle of (40 – x)° is (50 + x)°.

Question 14.
Find the measures of the supplements of the following angles:
i. 111°
ii. 47°
iii. 180°
iv. (90 – x)°
Solution:
i. Let the measure of the supplementary
angle be x°.
111 + x = 180
∴ 111 + x – 111 = 180 – 111
…..(Subtracting 111 from both sides)
∴ x = 69
∴ The supplementary angle of 111° is 69°.

ii. Let the measure of the supplementary angle be x°.
47 + x = 180
∴47 + x – 47 = 180 – 47
….(Subtracting 47 from both sides)
∴x = 133
∴The supplementary angle of 47° is 133°.

iii. Let the measure of the supplementary angle be x°.
180 + x = 180
∴180 + x – 180 = 180 – 180
….(Subtracting 180 from both sides)
∴x = 0
∴The supplementary angle of 180° is 0°.

iv. Let the measure of the supplementary angle be a°.
90 – x + a = 180
∴90 – x + a – 90 + x = 180 – 90+ x
….(Subtracting 90 and adding x on both sides)
∴a = 180 – 90 + x
∴a = (90 + x)
∴The supplementary angle of (90 – x)° is (90 + x)°.

Question 15.
Construct the following figures:
i. A pair of adjacent angles
ii. Two supplementary angles which are not adjacent angles.
iii. A pair of adjacent complementary angles.
Solution:
i.

ii.

iii.

Question 16.
In ∆PQR the measures of ∠P and ∠Q are equal and m∠PRQ = 70°, Find the measures of the following angles.

1. m∠PRT
2. m∠P
3. m∠Q

Solution:
Here, ∠PRQ and ∠PRT are angles in a linear pair.
m∠PRQ + m∠PRT = 180°
∴70 + m∠PRT = 180
∴m∠PRT = 180 – 70
∴m∠PRT = 110°
Now, ∠PRT is the exterior angle of ∆PQR.
∴m∠P + m∠Q = m∠PRT
∴m∠P + m∠P = m∠PRT ….(The measures of ∠P and ∠Q is same)
∴2m∠P = 110
∴m∠P = \(\frac { 110 }{ 2 }\)
∴m∠P = 55°
∴m∠Q =

Question 17.
Simplify
i. 5⁴ × 5³
ii. \(\left(\frac{2}{3}\right)^{6} \div\left(\frac{2}{3}\right)^{9}\)
iii. \(\left(\frac{7}{2}\right)^{8} \times\left(\frac{7}{2}\right)^{-6}\)
iv. \(\left(\frac{4}{5}\right)^{2} \div\left(\frac{5}{4}\right)\)
Solution:
Simplify
i. 5⁴ × 5³
= 5⁴⁺³
= 5⁷

ii. \(\left(\frac{2}{3}\right)^{6} \div\left(\frac{2}{3}\right)^{9}\)

iii. \(\left(\frac{7}{2}\right)^{8} \times\left(\frac{7}{2}\right)^{-6}\)

iv. \(\left(\frac{4}{5}\right)^{2} \div\left(\frac{5}{4}\right)\)

Question 18.
Find the value:
i. 17¹⁶  ÷ 17¹⁶
ii. 10^-3
iii. (2³)²
iv. 4⁶ × 4^-4
Solution:
i. 17¹⁶  ÷ 17¹⁶
= 17⁰
= 1

ii. 10^-3
= \(\frac{1}{10^{3}}\)
= \(\frac{1}{1000}\)

iii. (2³)²
= 2^3×2
= 2⁶
= 2 × 2 × 2 × 2 × 2 × 2
= 64

iv. 4⁶ × 4^-4
= 4^6+(-4)
= 4²
= 4 × 4
= 16

Question 19.
Solve:
i. (6a – 5b – 8c) + (15b + 2a – 5c)
ii. (3x + 2y) (7x – 8y)
iii. (7m – 5n) – (-4n – 11m)
iv. (11m – 12n + 3p) – (9m + 7n – 8p)
Solution:
i. (6a – 5b – 8c) + (15b + 2a – 5c)
= (6a + 2a) + (-5b + 15b) + (-8c – 5c)
= 8a + 10b – 13c

ii. (3x + 2y) (7x – 8y)
= 3x × (7x – 8y) + 2yx (7x – 8y)
= 21x² – 24xy + 14xy – 16y²
= 21x² – 10xy – 16y²

iii. (7m – 5n) – (-4n – 11m)
= 7m – 5n + 4n + 11m
= (7m + 11m) + (-5n + 4n)
= 18m – n

iv. (11m – 12n + 3p) – (9m + 7n – 8p)
= 11m – 12n + 3p – 9m – 7n + 8p
= (11m – 9m) + (-12n – 7n) + (3p + 8p)
= 2m – 19n + 11p

Question 20.
Solve the following equations:
i 4(x + 12) = 8
ii. 3y + 4 = 5y – 6
Solution:
i. 4(x + 12) = 8
∴4x + 48 = 8
∴4x + 48 – 48 = 8 – 48
….(Subtracting 48 from both sides)
∴ 4x = -40
∴ x = \(\frac { -40 }{ 4 }\)
∴ x = -10

ii. 3y + 4 = 5y – 6
∴ 3y + 4 + 6 = 5y – 6 + 6
….(Adding 6 on both sides)
∴ 3y + 10 = 5y
∴ 3y + 10 – 3y = 5y – 3y
….(Subtracting 3y from both sides)
∴ 10 = 2y
∴ 2y = 10
∴ y = \(\frac { 10 }{ 2 }\)
∴ y = 5