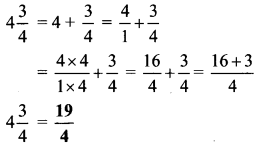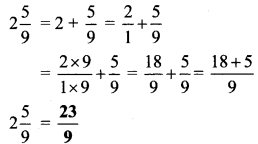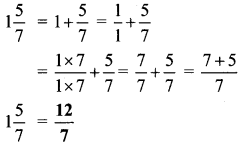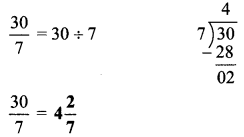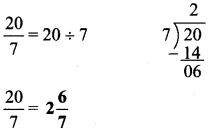Category: Class 6

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 5 (अ) आओ, आयु बताना सीखो, (ब) महाराष्ट्र की बेटी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 5 (अ) आओ, आयु बताना सीखो, (ब) महाराष्ट्र की बेटी

Hindi Sulabhbharti Class 6 Solutions Chapter 5 (अ) आओ, आयु बताना सीखो, (ब) महाराष्ट्र की बेटी Textbook Questions and Answers

अंतर बताओ:

Answer:
१. माँगटीके की बनावट अलग है।
२. शॉल का रंग अलग है।
३. बिंदिया का आकार अलग है।
४. हार के लोलक का रंग अलग है।
५. हाथ पर लगी मेंहदी की बनावट अलग है।
६. साड़ी के किनारे पर से चित्र गायब है।
७. चोली का रंग अलग है।
८. होंठ लाल है।
९. साड़ी का रंग अलग है।
१०. ठुड्डी पर तिल है।

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 4 जोकर Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 4 जोकर

Hindi Sulabhbharti Class 6 Solutions Chapter 4 जोकर Textbook Questions and Answers

किन्हीं पाँच मुहावरों / कहावतों के सांकेतिक चित्र बनाओ: जैसे

मैंने समझा:
Answer:
प्रस्तुत पाठ में मैंने सीखा कि अपनी बातों को प्रभावी ढंग से कम-से-कम शब्दों में व्यक्त करने के लिए मुहावरों और कहावतों का प्रयोग किया जाता है।

खोजबीन:

निम्नलिखित शब्द को लेकर चार मुहावरे लिखो।

Answer:
हाथ
१. हाथ का मैल होना
२. हाथ तंग होना
३. हाथ धोना
४. हाथ पर हाथ धरे बैठना

स्वयं अध्ययन:

अब पछताए होत क्या, जब चिड़िया चुग गई खेत’ पर आधारित कोई कहानी सुनाओ।
Answer:
चींटी और टिड्डा दोनों पड़ोसी थे। चींटी बहुत मेहनती थी। वह दिनभर मेहनत करती थी। वह अपने भविष्य के लिए भी अनाज इकट्ठा करती रहती थी। वहीं टिड्डा सिर्फ पेट भरने तक का भोजन जुटाकर दिनभर खेलता-कूदता, नाचता-गाता था। कुछ दिनों बाद बरसात का मौसम आया। टिड्डे को । कहीं भी भोजन नहीं मिल पा रहा था, जबकि चींटी आराम से घर में बैठकर बरसात का आनंद ले रही थी। चींटी को देखकर टिड्डे को यह भी समझ में आ गया कि उसने पूरे साल आराम करके गलती की, लेकिन ‘अब पछताए होत क्या, जब चिड़िया चुग गई खेत।’

जरा सोचो ………. बताओ:

यदि साइकिल तुमसे बोलने लगी तो ……
Answer:
यदि साइकिल मुझसे बोलने लगी तो मुझे बहुत खुशी होगी। मैं उससे अपने मन की सारी बातें कहता और वह भी मुझे अपनी सारी बातें बताती।। हम दोनों आपस में बहुत बातें करते। मैं उसे अपनी सबसे अच्छी दोस्त बना लेता और वह बिना मेहनत किए मुझे मेरी मनचाही जगह पर ले जाती। यदि साइकिल मुझसे बोलने लगी, तो मैं उसके सारे दुख-दर्द भी पूगा। सब उस पर सवार होते हैं, उसपर सामान रखते हैं, तो उसे कैसा महसूस होता है? मैं उसकी नजर से दिखने वाली दुनिया के बारे में जानना चाहूँगा। साइकिल जिन-जिन स्थानों का भ्रमण कर चुकी होगी, उन सभी स्थानों के बारे में भी जानकारी लूँगा। यदि साइकिल मुझसे बोलने लगी, तो मैं उसके इतिहास के बारे में जानना चाहूँगा। उसका जन्म कब, कैसे और कहाँ हुआ? इन सबकी जानकारी लूँगा। उससे पूछंगा कि वह पहले किस तरह दिखती थी? उसे पहले यह दुनिया कैसी लगती थी और अब कैसी लगती है? उसकी हालत में कैसे बदलाव आया? साइकिल से ढेर सारी बातें करके उसे अपनेपन का विश्वास दिलाऊँगा तथा उसकी हालत को बेहतर-सेबेहतर बनाने का प्रयत्न करूँगा।

विचार मंथन:

गागर में सागर भरना
Answer:
‘गागर में सागर भरना’ यह एक मुहावरा है। इस मुहावरे का अर्थ है – कम शब्दों में बहुत कुछ कहना। इस मुहावरे को एक उदाहरण द्वारा समझते हैं – कबीरदास ने अपने दोहों के जरिए गागर में सागर भर दिया।

सदैव ध्यान में रखो:

हमें सदैव प्रसन्न रहना चाहिए।
Answer:
हास्य का मतलब होता है हँसना। हँसना स्वास्थ्य के लिए बहुत लाभदायक है। हँसने से रक्त संचार बढ़ता है। हँसने से चेहरे की माँसपेशियों का भी व्यायाम होता है। इससे दिमाग भी स्वस्थ रहता है। यूँ कहा जा सकता है कि हँसना स्वास्थ्य के लिए बहुत गुणकारी है, इसलिए हमें हँसते रहना चाहिए।

समझो हमें:

चित्र की सहायता से बारहखड़ी के शब्द बनाकर लिखो।

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 4 Operations on Fractions Class 6 Practice Set 9 Answers Solutions.

6th Standard Maths Practice Set 9 Answers Chapter 4 Operations on Fractions

Question 1.
Convert into improper fractions:
i. \(7 \frac{2}{5}\)
ii. \(5 \frac{1}{6}\)
iii. \(4 \frac{3}{4}\)
iv. \(2 \frac{5}{9}\)
v. \(1 \frac{5}{7}\)
Solution:
i. \(7 \frac{2}{5}\)

ii. \(5 \frac{1}{6}\)

iii. \(4 \frac{3}{4}\)

iv. \(2 \frac{5}{9}\)

v. \(1 \frac{5}{7}\)

Question 2.
Convert into mixed numbers:
i. \(\frac { 30 }{ 7 }\)
ii. \(\frac { 7 }{ 4 }\)
iii. \(\frac { 15 }{ 12 }\)
iv. \(\frac { 11 }{ 8 }\)
v. \(\frac { 21 }{ 4 }\)
v. \(\frac { 20 }{ 7 }\)
Solution:
i. \(\frac { 30 }{ 7 }\)

ii. \(\frac { 7 }{ 4 }\)

iii. \(\frac { 15 }{ 12 }\)

iv. \(\frac { 11 }{ 8 }\)

v. \(\frac { 21 }{ 4 }\)

v. \(\frac { 20 }{ 7 }\)

Question 3.
Write the following examples using fraction:
i. If 9 kg rice is shared among 5 people, how many kilograms of rice does each person get?
ii. To make 5 shirts of the same size, 11 meters of cloth is needed. How much cloth is needed for one shirt?
Solution:
i. Total quantity of rice = 9 kg
Number of people = 5
∴ Kilograms of rice received by each person = \(\frac { 9 }{ 5 }\)
∴ Each person will get \(\frac { 9 }{ 5 }\) kg of rice.

ii. Total meters of cloth = 11 meters
Number of shirts to be made = 5
Meters of cloth needed to make 1 shirt = \(\frac { 11 }{ 5 }\)
∴ Cloth needed to make 1 shirt is \(\frac { 11 }{ 5 }\) meters.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 16 Quadrilaterals Class 6 Practice Set 37 Answers Solutions.

6th Standard Maths Practice Set 37 Answers Chapter 16 Quadrilaterals

Question 1.
Observe the figures below and find out their names:

Solution:
i. Pentagon (5 sides)
ii. Hexagon (6 sides)
iii. Heptagon (7 sides)
iv. Octagon (8 sides)

Maharashtra Board Class 6 Maths Chapter 16 Quadrilaterals Practice Set 37 Intext Questions and Activities

Question 1.
Observe the figures given below and say which of them are quadrilaterals. (Textbook pg. no. 81)

Solution:
Is a quadrilateral: (i)

Question 2.
Draw a quadrilateral. Draw one diagonal of this quadrilateral and divided it into two triangles. Measures all the angles in the figure. Is the sum of the measures of the four angles of the quadrilateral equal to the sum of the measures of the six angles of the two triangles? Verity that this is so with other quadrilaterals. (Textbook pg. no. 84)
Solution:

m∠PQR = 104°
m∠QRP = 26°
m∠RPQ = 50°
m∠PRS = 34°
m∠RSP = 106°
m∠SPR = 40°
∴ Sum of the measures of the angles of quadrilateral = m∠PQR + m∠QRP + m∠RPQ + m∠PRS + m∠RSP + m∠SPR
= 104° + 26° + 50° + 34° + 106° + 40°
= 360°
Also, we observe that
Sum of the measures of the angles of quadrilateral = Sum of the measures of angles of the two triangles (PQR and PRS)
= (104°+ 26°+ 50°)+ (34° + 106° + 40°)
= 180° + 180°
= 360°
[Note: Students should drew different quadrilaterals and verify the property.]

Question 3.
For the pentagon shown in the figure below, answer the following: (Textbook pg. no. 84)

1. Write the names of the five vertices of the pentagon.
2. Name the sides of the pentagon.
3. Name the angles of the pentagon.
4. See if you can sometimes find players on a field forming a pentagon.

Solution:

1. The vertices of the pentagon are points A, B, C, D and E.
2. The sides of the pentagon are segments AB, BC, CD, DE and EA.
3. The angles of the pentagon are ∠ABC, ∠BCD, ∠CDE, ∠DEA and ∠EAB.
4. The players shown in the above figure form a pentagon. The players are standing on the vertices of

Question 4.
Cut out a paper in the shape of a quadrilateral. Make folds in it that join the vertices of opposite angles. What can these folds be called? (Textbook pg. no. 83)

Solution:
The folds are called diagonals of the quadrilateral.

Question 5.
Take two triangular pieces of paper such that . one side of one triangle is equal to one side of the other. Let us suppose that in ∆ABC and ∆PQR, sides AC and PQ are the equal sides. Join the triangles so that their equal sides lie B side by side. What figure do we get? (Textbook pg. no. 83)

Solution:
If we place the triangles together such that the equal sides overlap, the two triangles form a quadrilateral.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 13 Profit-Loss Class 6 Practice Set 33 Answers Solutions.

6th Standard Maths Practice Set 33 Answers Chapter 13 Profit-Loss

Question 1.
Maganlal bought trousers for Rs 400 and a shirt for Rs 200 and sold them for Rs 448 and Rs 250 respectively. Which of these transactions was more profitable?
Solution:
Cost price of trousers = Rs 400
Selling price of trousers = Rs 448
Profit = Selling price – Cost price
= 448 – 400 = Rs 48
Let Maganlal make x % profit on selling trousers

∴ x = 12%
Cost price of shirt = Rs 200
Selling price of shirt = Rs 250
∴ Profit = Selling price – Cost price
= 250 – 200
= Rs 50
Let Maganlal make y% profit on selling shirt.

∴ y = 25%
∴ Transaction involving selling of shirt was more profitable.

Question 2.
Ramrao bought a cupboard for Rs 4500 and sold it for Rs 4950. Shamrao bought a sewing machine for Rs 3500 and sold it for Rs 3920. Whose transaction was more profitable?
Solution:
Cost price of cupboard = Rs 4500
Selling price of cupboard = Rs 4950
∴ Profit = Selling price – Cost price
= 4950 – 4500
= Rs 450
Let Ramrao make x% profit on selling cupboard

∴ x = 10%
Cost price of sewing machine = Rs 3500
Selling price of sewing machine = Rs 3920
∴Profit = Selling price – Cost price
= 3920 – 3500
= Rs 420
Shamrao make y% profit on selling sewing machine.

∴y = 12%
∴Shamrao’s transaction was more profitable.

Question 3.
Hanif bought one box of 50 apples for Rs 400. He sold all the apples at the rate of Rs 10 each. Was there a profit or loss? What was its percentage?
Solution:
Cost price of 50 apples = Rs 400
Selling price of one apple = Rs 10
∴ Selling price of 50 apples = 10 x 50 = Rs 500
Selling price is greater than the total cost price.
∴ Hanif made a profit.
∴ Profit = Selling price – Cost price
= 500 – 400
= Rs 100
Let Hanif make of x% profit on selling apples.

∴ x = 25%
∴ Hanif made a profit of 25%.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 9 HCF-LCM Class 6 Practice Set 24 Answers Solutions.

6th Standard Maths Practice Set 24 Answers Chapter 9 HCF-LCM

Question 1.
Find the HCF of the following numbers.
i. 45, 30
ii. 16, 48
iii. 39, 25
iv. 49, 56
v. 120, 144
vi. 81, 99
vii. 24, 36
viii. 25, 75
ix. 48, 54
x. 150, 225
Solution:
i. Factors of 45 = 1, 3, 5, 9,15, 45
Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30
∴ HCF of 45 and 30 = 15

ii. Factors of 16 = 1, 2, 4, 8, 16
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
∴ HCF of 16 and 48 = 16

iii. Factors of 39 = 1, 3, 13, 39
Factors of 25 = 1, 5, 25
∴ HCF of 39 and 25 = 1

iv. Factors of 49 = 1, 7, 49
Factors of 56 = 1, 2, 4, 7, 8, 14, 28, 56
∴ HCF of 49 and 56 = 7

v. Factors of 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Factors of 144 = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144
∴ HCF of 120 and 144 = 24

vi. Factors of 81 = 1, 3, 9, 27, 81
Factors of 99 = 1, 3, 9, 11, 33, 99
∴ HCF of 81 and 99 = 9

vii. Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
∴ HCF of 24 and 36 = 12

viii. Factors of 25 = 1, 5, 25
Factors of 75 = 1, 3, 5, 15, 25, 75
∴ HCF of 25 and 75 = 25

ix. Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Factors of 54 = 1, 2, 3, 6, 9, 18, 27, 54
∴ HCF of 48 and 54 = 6

x. Factors of 150 = 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
Factors of 225 = 1, 3, 5, 9, 15, 25, 45, 75, 225
∴ HCF of 150 and 225 = 75

Question 2.
If large square beds of equal size are to be made for planting vegetables on a plot of land 18 metres long and 15 metres wide, what is the maximum possible length of each bed?
Solution:
Length of the land = 18 m
Width of the land = 15 m
The maximum length of each bed will be the greatest common factor of 18 and 15.
Factors of 18 = 1, 2, 3, 6, 9, 18
Factors of 15 = 1, 3, 5, 15
∴ HCF of 18 and 15 = 3
∴ The maximum possible length of each bed is 3 metres.

Question 3.
Two ropes, one 8 metres long and the other 12 metres long are to be cut into pieces of the same length. What will the maximum possible length of each piece be?
Solution:
Length of first rope = 8 m
Length of second rope = 12 m
The maximum length of each piece will be the greatest common factor of 8 and 12.
Factors of 8 = 1, 2, 4, 8
Factors of 12 = 1, 2, 3, 4, 6, 12
∴ HCF of 8 and 12 = 4
∴ The maximum possible length of each piece is 4 metres.

Question 4.
The number of students of Std 6th and Std 7th who went to visit the Tadoba Tiger Project at Chandrapur was 140 and 196 respectively. The students of each class are to be divided into groups of the same number of students. Each group can have a paid guide. What is the maximum number of students that can be there in each group? Why do you think each group should have the maximum possible number of students?
Solution:
Number of students of Std 6th = 140
Number of students of Std 7th = 196
The maximum number of students in each group will be the greatest common factor of 140 and 196.
Factors of 140 = 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
Factors of 196 = 1, 2, 4, 7, 14, 28, 49, 98, 196
∴ HCF of 140 and 196 = 28
∴ Maximum students in each group are 28.
Each group should have maximum number students so that there will be minimum number of groups and hence minimum number of paid guides.

Question 5.
At the Rice Research Centre at Tumsar there are 2610 kg of seeds of the basmati variety and 1980 kg of the indrayani variety. If the maximum possible weight of seeds has to be filled to make bags of equal weight what would be the weight of each bag? How many bags of each variety will there be?
Solution:
Weight of basmati rice = 2610 kg
Weight of indrayani rice = 1980 kg
The weight of each bag will be the greatest common factor of 2610 and 1980.
Factors of 2610 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 29, 30, 45, 58, 87, 90, 145, 174, 261, 290, 435, 522, 870, 1305, 2610
Factors of 1980 = 1, 2, 3, 4, 5, 6, 9, 10, 11, 12, 15, 18, 20, 22, 30, 33, 36, 44, 45, 55, 60, 66, 90, 99, 110, 132, 165, 180, 198, 220, 330, 396, 495, 660, 990, 1980
∴ HCF of 2610 and 1980 = 90
Maximum weight of each bag = 90 kg
Number of bags of basmati rice = 2610 ÷ 90 = 29
Number of bags of indrayani rice = 1980 ÷ 90 = 22
Maximum weight of each bag is 90 kg.
The number of bags of basmati rice is 29, and the number of bags of indrayani rice is 22.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 2 Angles Class 6 Practice Set 3 Answers Solutions.

6th Standard Maths Practice Set 3 Answers Chapter 2 Angles

Question 1.
Use the proper geometrical instruments to construct the following angles. Use the compass and the ruler to bisect them:

1. 50°
2. 115°
3. 80°
4. 90°

Solution:

Maharashtra Board Class 6 Maths Chapter 2 Angles Practice Set 3 Intext Questions and Activities

Question 1.
Construct an angle bisector to obtain an angle of 30°. (Textbook pg. no. 11)
Solution: .
In order to get a bisected angle of a given measure, the student has to draw the angle having twice the measurement of required bisected angle.

For getting measurement of 30° (for the bisected angle), one has to make an angle of 60° (i.e. 30° × 2).

Step 1:
Draw ∠ABC of 60°.

Step 2:
Cut arcs on the rays BA and BC. Name these points as D and E respectively.

Step 3:
Place the compass point on point D and draw an arc inside the angle.
Without changing the distance of the compass, place the compass point on point E and cut the previous arc. Name the point of intersection as O

Step 4:
Draw ray BO.
Ray BO is the angle bisector of ∠ABC.
i.e. m∠ABO = m∠CBO = 30°

Question 2.
Construct an angle bisector to draw an angle of 45°. (Textbook pg. no. 11)
Solution:
For getting measurement of 45° (for the bisected angle), one has to make an angle of 90° (i.e. 45° × 2).
Step 1:
Draw ∠PQR of 90°.

Step 2:
Cut arcs on the rays QP and QR.
Name these points as M and N respectively.

Step 3:
Place the compass point on point M and draw an arc inside the angle.
Without changing the distance of the compass, place the compass point on point N and cut the

Step 4:
Draw ray QO.
Ray QO is the angle bisector of ∠PQR.
i.e. m∠PQO = m∠RQO = 45°

Question 3.
Ask three or more children to stand in a straight line. Take two long ropes. Let the child in the middle hold one end of each rope. With the help of the ropes, make the children on either side stand along a straight line. Tell them to move so as to form an acute angle, a right angle, an obtuse angle, a straight angle, a reflex angle and a full or complete angle in turn. Keeping the rope stretched will help to ensure that the children form straight lines. (Textbook pg. no. 6)
Solution:

Question 4.
Look at the pictures below and identify the different types of angles. (Textbook pg. no. 8)

Solution:
i. Complete angle
ii. Reflex and Acute angle
iii. Acute and Obtuse angle

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 5 Decimal Fractions Class 6 Practice Set 15 Answers Solutions.

6th Standard Maths Practice Set 15 Answers Chapter 5 Decimal Fractions

Question 1.
Write the proper number in the empty boxes.

Solution:

Question 2.
Convert the common fractions into decimal fractions:
i. \(\frac { 3 }{ 4 }\)
ii. \(\frac { 4 }{ 5 }\)
iii. \(\frac { 9 }{ 8 }\)
iv. \(\frac { 17 }{ 20 }\)
v. \(\frac { 36 }{ 40 }\)
vi. \(\frac { 7 }{ 25 }\)
vii. \(\frac { 19 }{ 200 }\)
Solution:
i. \(\frac { 3 }{ 4 }\)

ii. \(\frac { 4 }{ 5 }\)

iii. \(\frac { 9 }{ 8 }\)

iv. \(\frac { 17 }{ 20 }\)

v. \(\frac { 36 }{ 40 }\)

vi. \(\frac { 7 }{ 25 }\)

vii. \(\frac { 19 }{ 200 }\)

Question 3.
Convert the decimal fractions into common fractions:
i. 27.5
ii. 0.007
iii. 90.8
iv. 39.15
v. 3.12
vi. 70.400
Solution:
i. 27.5
= \(\frac { 275 }{ 10 }\)

ii. 0.007
= \(\frac { 7 }{ 1000 }\)

iii. 90.8
= \(\frac { 908 }{ 10 }\)

iv. 39.15
= \(\frac { 3915 }{ 100 }\)

v. 3.12
= \(\frac { 312 }{ 100 }\)

vi. 70.400
= 70.4
= \(\frac { 704 }{ 10 }\)

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 10 Equations Class 6 Practice Set 27 Answers Solutions.

6th Standard Maths Practice Set 27 Answers Chapter 10 Equations

Question 1.
Rewrite the following using a letter:
i. The sum of a certain number and 3.
ii. The difference is obtained by subtracting 11 from another number.
iii. The product of 15 and another number.
iv. Four times a number is 24.
Solution:
i. Let the number be x.
∴ x + 3 represents the sum of a certain number x and 3.

ii. Let the number be x.
∴ x – 11 represents the number obtained by subtracting 11 from another number x.

iii. Let the number be x.
∴ 15x represents the product of 15 and another number x.

iv. Let the number be x.
∴ 4x = 24 represents four the product of a number x four times.

Question 2.
Find out which operation must be done on both sides of these equations in order to solve them:

1. x + 9 = 11
2. x – 4 = 9
3. 8x = 24
4. \(\frac { x }{ 6 }\) = 3

Solution:

1. Subtract 9 from both sides.
2. Add 4 to both sides.
3. Divide both sides by 8.
4. Multiply both sides by 6.

Question 3.
Given below are some equations and the values of the variables. Are these values the solutions to those equations?

No.	Equation	Value of the Variable	Solution (Yes/No)
i.	y – 3 = 11	y = 3	No
ii.	17 = n + 7	n = 10
iii.	30 = 5x	x = 6
iv.	\(\frac { m }{ 2 }\) = 14	m = 7

Solution:

No.	Equation	Value of the Variable	Solution (Yes/No)
i.	y – 3 = 11	y = 3	No
ii.	17 = n + 7	n = 10	Yes
iii.	30 = 5x	x = 6	Yes
iv.	\(\frac { m }{ 2 }\) = 14	m = 7	No

i. y – 3 = 11
∴ y – 3 + 3 = 11 + 3
…. (Adding 3 to both sides)
∴ y + 0 = 14
∴ y = 14

ii. 17 = n + 7
∴ 17 – 7 = n + 7 – 7
…. (Subtracting 7 from both sides)
∴ 17 + (-7) = n + 7 – 7
∴ 10 = n
∴  n = 10

iii. 30 = 5x
∴ \(\frac{30}{5}=\frac{5x}{5}\)
…. (Dividing both sides by 5)
∴  6 = 1x
∴ 6 = x
∴  x = 6

iv. \(\frac { m }{ 2 }\) = 14
∴ \(\frac { m }{ 2 }\) × 2 = 14 × 2
…. (Multiplying both sides by 2)
\(\frac { m\times2 }{ 2\times1 }\) = 28
∴ m = 28

Question 4.
Solve the following equations:
i. y – 5 = 1
ii. 8 = t + 5
iii. 4x = 52
iv. 19 = m – 4
v. \(\frac { p }{ 4 }=9\)
vi. x + 10 = 5
vi. m – 5 = -12
vii. p + 4 = -1
Solution:
i. y – 5 = 1
∴y – 5 + 5 = 1 + 5
…. (Adding 5 to both sides)
∴y + 0 = 6
∴y = 6

ii. 8 = t + 5
∴8 – 5 = t + 5 – 5
……(Subtracting 5 from both sides)
∴8 + (-5) = t + 0
∴ 3 = t
∴t = 3

iii. 4x = 52
∴\(\frac{4x}{4}=\frac{52}{4}\)
…. (Dividing both sides by 4)
∴ 1x = 13
∴ x = 13

iv. 19 = m -4
∴ 19 + 4 = m – 4 + 4
…. (Adding 4 to both sides)
∴ 23 = m + 0
∴ m = 23

v. \(\frac { p }{ 4 }\) = 9
∴ \(\frac { p }{ 4 }\) × 4 = 9 × 4 …. (Multiplying both sides by 4)
∴ \(\frac { p\times4 }{ 4\times1 }=36\)
∴ 1p = 36
∴ p = 36

vi. x + 10 = 5
∴ x + 10 – 10 = 5 – 10
…. (Subtracting 10 from both sides)
∴ x + 0 = 5 + (-10)
∴ x = -5

vii. m – 5 = -12
∴m – 5 + 5 = – 12 + 5
…. (Adding 5 to both sides)
∴m + 0 = -7
∴m = -7

viii. p + 4 = – 1
∴p + 4 – 4 = -1 – 4
…. (Subtracting 4 from both sides)
∴p + 0 = (-1) + (-4)
∴P = -5

Question 5.
Write the given information as an equation and find its solution:
i. Haraba owns some sheep. After selling 34 of them in the market, he still has 176 sheep. How many sheep did Haraba have at first?

ii. Sakshi prepared some jam at home and filled it in bottles. After giving away 7 of the bottles to her friends she still has 12 for herself. How many bottles had she made in all? If she filled 250g of jam in each bottle, what was the total weight of the jam she made?

iii. Archana bought some kilograms of wheat. She requires 12 kg per month and she got enough wheat milled for 3 months. After that, she had 14 kg left. How much wheat had Archana bought altogether?
Solution:
i. Let the number of sheep before selling be x.
∴ x – 34 = 176
∴ x – 34 + 34 = 176 + 34 ….(Adding 34 to both sides)
∴ x + 0 = 210
∴ x = 210
The number of sheep with Haraba before selling is 210.

ii. Let the total number of bottles be x.
∴ x – 7 = 12
∴ x – 7 + 7 = 12 + 7 ….(Adding 7 to both sides)
∴ x + 0 = 19
∴ x = 19
Weight of jam in each bottle = 250g
∴ Total weight of jam = 19 × 250g = 4750 g = \(\frac { 4750 }{ 1000 }\)kg = 4.75 kg
∴ The total number of bottles of jam made by Sakshi is 19, and the total weight of jam made is 4.75 kg.

iii. Let the total wheat bought by Archana be x kg.
Wheat used in 1 month = 12 kg
∴ Wheat used in 3 months = 3 × 12 = 36 kg
∴ x – 36 = 14
∴ x – 36 + 36 = 14 + 36 ….(Adding 36 to both sides)
∴ x + 0 = 50
∴ x = 50
∴ The total amount of wheat bought by Archana was 50 kg.