Category: Class 6

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 6 स्वास्थ्य संपदा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 6 स्वास्थ्य संपदा

Hindi Sulabhbharti Class 6 Solutions Chapter 6 स्वास्थ्य संपदा Textbook Questions and Answers

कार्य हमारा

चित्र देखकर क्रियायुक्त शब्दों से वाक्य बनाओ।

Answer:

1. लता सेब खाती है।
2. बच्चे हँस रहे थे।
3. गुड़िया अलमारी से गिर गई है।
4. माँ अपने बच्चे को सुला रही है।
5. रमेश अपनी बहन को खाना खिला रहा है।
6. मैं अपने-आप खाना खा लेता हूँ।
7. माँ अपनी बिटिया को खाना खिलाती है।

जरा सोचो…..लिखो:

यदि भोजन से नमक गायब हो जाए तो….
Answer:
यदि भोजन से नमक गायब हो जाए तो भोजन स्वादिष्ट नहीं लगेगा। हर चीज फीकी लगेगी। फीका भोजन करना मुश्किल होगा और हमारा पेट नहीं भरेगा। पेटभर खाना न खाने से हमें कमजोरी आ जाएगी। हम ढंग से कोई काम नहीं कर सकेंगे। नमक के बिना हमारे शरीर को आयोडीन नहीं मिलेगा, जिससे शरीर का विकास रुक जाएगा।

मैंने समझा:

__________
___________
Answer:
इस पाठ में गांधी जी यह समझाना चाहते हैं कि हमें अपना शरीर स्वस्थ रखना चाहिए। हमें पर्याप्त मात्रा में दूध, मक्खन, फल, हरी सब्जियाँ, गेहूँ की रोटी आदि पौष्टिक पदार्थ अपने भोजन में लेने चाहिए। हमें शुद्ध हवा में रहते हुए प्राणायाम व व्यायाम भी करना चाहिए।

खोजबीन:

खादी का कपड़ा कैसे बनाया जाता है इसकी जानकारी प्राप्त करके लिखो।
Answer:
चरखे पर रूई से सूत काता जाता है। फिर उस सूत से जुलाहा हथकरघे पर कपड़ा बुनता है। इसके पश्चात इस कपड़े को रंगा जाता है। हाथ से बुना कपड़ा कुछ मोटा होता है। इसी कपड़े को खादी कहते हैं।

अध्ययन कौशल:

पढ़ाई का नियोजन करते हुए अपनी दिनचर्या लिखो।
Answer:
मेरा स्कूल सुबह साढ़े सात बजे से दोपहर दो बजे तक रहता है। मैं ढाई बजे घर आ जाता हूँ। खाना खाने और थोड़ा आराम करने के बाद मैं अपने स्कूल का गृहकार्य करने बैठ जाता हूँ। फिर गृहकार्य पूरा कर मैं खेलने चला जाता हूँ, क्योंकि मेरी उम्र के सभी बच्चे उसी समय अपनी पढ़ाई आदि खत्म करके खेलने आते हैं। दो घंटा खेलने के बाद मैं घर आता हूँ। खाना खाते समय मैं टीवी पर समाचार और डिस्कवरी जैसे ज्ञानवर्धक चैनल देखता हूँ। फिर स्कूल बैग तैयार करके दस बजे मैं सोने चला जाता हूँ। इस तरह यह मेरी दिनचर्या सुबह से रात तक की है।

बताओ तो सही।

संतुलित आहार पर पाँच वाक्य बोलो।
Answer:

1. पर्याप्त मात्रा में पौष्टिक तत्त्वों से भरे आहार को संतुलित आहार’ कहते हैं।
2. मजबूत एवं स्वस्थ शरीर के लिए संतुलित आहार लेना चाहिए।
3. संतुलित आहार हमारे कार्य करने की शक्ति एवं गति को बढ़ाता है।
4. इससे हमारे शरीर का संपूर्ण रूप से शारीरिक एवं मानसिक विकास होता है।
5. संतुलित आहार हमारे शरीर की रोग-प्रतिरोधक क्षमता बढ़ाता है।

मेरी कलम से:

अपने मित्र को शुभकामना/बधाई पत्र लिखो।
Answer:

एक वाक्य में उत्तर लिखो।

Question 1.
जैतून के तेल की जगह मक्खन क्यों लिया जाना चाहिए?
Answer:
मक्खन में जो विटामिन होते हैं वह जैतून के तेल में नहीं होते, इसलिए जैतून के तेल की जगह मक्खन लिया जाना चाहिए।

Question 2.
रक्षक का धर्म कौन-सा है?
Answer:
रक्षा करना रक्षक का धर्म है।

Question 3.
किन-किन सब्जियों की गिनती अच्छी, हरी सब्जियों में होती है?
Answer:
लौकी, फूलगोभी, पत्तागोभी, बिना बीज की सेम, बैंगन आदि की गिनती अच्छी और हरी सब्जियों में होती है।

Question 4.
फेफड़ों के लिए क्या अति आवश्यक है?
Answer:
चौबीसों घंटे शुद्ध-से-शुद्ध हवा फेफड़ों के लिए अति आवश्यक है।

सदैव ध्यान में रखो:

नवयुवकों की शक्ति देशहित में लगनी चाहिए।
Answer:
मनुष्य के अंदर उसके पूरे जीवन में सबसे अधिक ऊर्जा युवावस्था में होती है। इस उम्र में वह अधिक-से-अधिक मुश्किल कार्य कर सकता है। मनुष्य का कर्तव्य होता है कि वह अपने परिवार और समाज के साथ-साथ देश के विकास के लिए भी कार्य करे। अत: नवयुवक या युवावर्ग को अपनी शक्ति देशहित में लगानी चाहिए, जिससे देश ज्यादा-से-ज्यादा सफलता प्राप्त कर सके।

विचार मंथन:

स्वस्थ शरीर, स्वस्थ मन। योगासन है, उत्तम साधन।
Answer:
स्वास्थ्य सबसे बड़ा धन है। अच्छे स्वास्थ्य के बिना सब कुछ व्यर्थ है। कहते हैं कि स्वस्थ शरीर में स्वस्थ मन वास करता है, इसलिए हमें हमेशा अपने स्वास्थ्य पर ध्यान देना चाहिए। इसके लिए अच्छे खान-पान के साथ-साथ शारीरिक व्यायाम भी अनिवार्य है। हमें सुबह जल्दी उठना चाहिए और रात को भी समय पर सो जाना चाहिए। सुबह उठकर खुली हवा में सैर करना लाभदायक होता है। साथ ही हमें योगासन भी अवश्य करना चाहिए। योगासन में शारीरिक क्रियाओं के अलावा श्वासोच्छवास पर ध्यान केंद्रित किया जाता है। इस तरह शारीरिक और मानसिक शक्तियों का विकास होता है। अत: स्वस्थ तन-मन के लिए योगासन एक उत्तम साधन है।

भाषा की ओर:

निम्न विशेषण शब्द का अपने वाक्य में प्रयोग करके उनका प्रकार लिखो।

Answer:

1. पाँच
   प्रकार: पाँच – संख्यावाचक विशेषण
   वाक्य: मैं रोज सुबह पाँच बजे सोकर उठता हूँ।
2. यही
   प्रकार: यही – सार्वनामिक विशेषण
   वाक्य: यही लड़का कल स्कूल नहीं आया था।
3. कुछ
   प्रकार: कुछ – परिमाणवाचक विशेषण
   वाक्य: कुछ फल लेते आना।
4. मीठी
   प्रकार: मीठी – गुणवाचक विशेषण
   वाक्य: रीना मीठी दही खाती है।

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 7 नदी कंधे पर Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions Chapter 7 नदी कंधे पर

Hindi Sulabhbharti Class 6 Solutions Chapter 7 नदी कंधे पर Additional Important Questions and Answers

निम्नलिखित प्रश्नों के उत्तर एक शब्द में लिखिए:

Question 1.
बालक किसको कंधे पर लाना चाहता है?
Answer:
नदी को।

Question 2.
बालक किसके साथ नहाना चाहता है?
Answer:
मित्रों के साथ।

Question 3.
वह नदी का परिचय किससे कराना चाहता है?
Answer:
भद्रजनों से।

निम्नलिखित प्रश्नों के उत्तर लिखिए:

Question 1.
बालक नदी के उस पार खड़े-खड़े क्या करना चाहता
Answer:
बालक नदी के उस पार खड़े-खड़े ‘मम्मी-मम्मी’ चिल्लाना चाहता है।

Question 2.
शाम ढलने पर बालक क्या करता?
Answer:
शाम ढलने पर बालक नदी को उठाकर अपने कंधे पर रखवाता और जहाँ से उसे लाया था, वहीं रख आता।

Question 3.
वह मित्रों के साथ किस प्रकार नहाना चाहता है?
Answer:
वह मित्रों के साथ कूद-कूदकर और उछल-उछलकर नहाना चाहता है।

Question 4.
बालक नदी को कहाँ बहाना चाहता है?
Answer:
बालक नदी को अपने घर के ठीक सामने बहाना चाहता है।

Question 5.
बालक सबको किसलिए आमंत्रित करता?
Answer:
बालक सबको नदी में नहाने के लिए आमंत्रित करता।

कविता में आए हुए लयात्मक शब्दों को ढूँढकर लिखिए:

उदाहरण: बहाते – बहाते

1. मस्ताते
2. रखवाते
3. करवाते

Answer:

1. चिल्लाते
2. रख आते
3. इतराते

रिक्त स्थानों की पूर्ति कीजिए:

Question 1.
अगर हमारे ……………… में होता।
Answer:
बस

Question 2.
……………… उठाकर घर ले आते।
Answer:
नदी

Question 3.
अपने घर के ठीक ………….
Answer:
सामने

Question 4.
उसको हम ……………… बहाते।
Answer:
हर रोज़

Question 5.
……………… उछल-उछलकर।
Answer:
कूद-कूदकर

Question 6.
अपने मित्रों के साथ ………………।
Answer:
चहाते

उचित जोड़ियाँ मिलाइए:

Answer:
१ – घ
२ – ग
३ – क
४ – ड
५ – ख

व्याकरण और भाषाभ्यास

निम्नलिखित शब्दों के बहुवचन-रूप लिखिए:

1. नदी
2. कंधा
3. बहाता

Answer:

1. नदियाँ
2. कंधे
3. बहाते

निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:

1. घर
2. नदी
3. आमंत्रित
4. शाम
5. मम्मी
6. मित्र
7. झटपट
8. इतराते

Answer:

1. गृह
2. सरिता
3. निमंत्रित
4. संध्या
5. माता
6. सखा
7. जल्दी-जल्दी
8. इठलाते

निम्नलिखित शब्दों के विपरीतार्थक शब्द लिखिए:

1. खड़े-खड़े
2. यहीं
3. उपस्थित
4. झटपट
5. सामने
6. भद्र

Answer:

1. बैठे-बैठे
2. वहीं
3. अनुपस्थित
4. धीरे-धीरे
5. पीछे
6. अभद्र

निम्नलिखित शब्दों में अनुस्वार ‘ या अनुनासिक लगाकर शब्द लिखिए:

1. मित्रो
2. कधे
3. जहा
4. आमत्रित
5. जनो

Answer:

1. मित्रों
2. कंधे
3. जहाँ
4. आमंत्रित
5. जनों

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati Chapter 9 वह देश कौन-सा है? Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions स्वयं अध्ययन २

Hindi Sulabhbharti Class 6 Solutions स्वयं अध्ययन २ Textbook Questions and Answers

चित्रवाचन करके अपने शब्दों में कहानी लिखो और उचित शीर्षक बताओ:

विद्यार्थियों से ऊपर दिए गए चित्रों का क्रमानुसार निरीक्षण कराएँ । चित्र में कौन-कौन-सी घटनाएं घटी होंगी, उन्हें सोचने के लिए कहें । उन्हें अन्य चित्रों एवं घटनाओं के आधार पर कहानी लिखने के लिए प्रेरित करें और उचित शीर्षक देने के लिए कहें।
Answer:
छात्र स्वयं करें

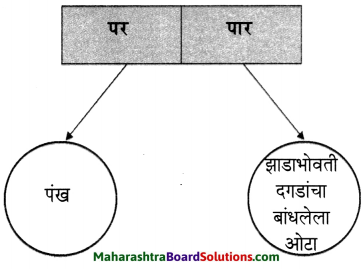
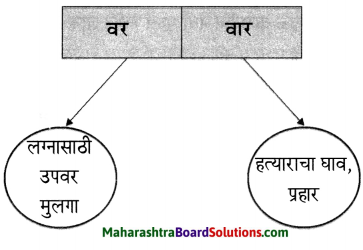
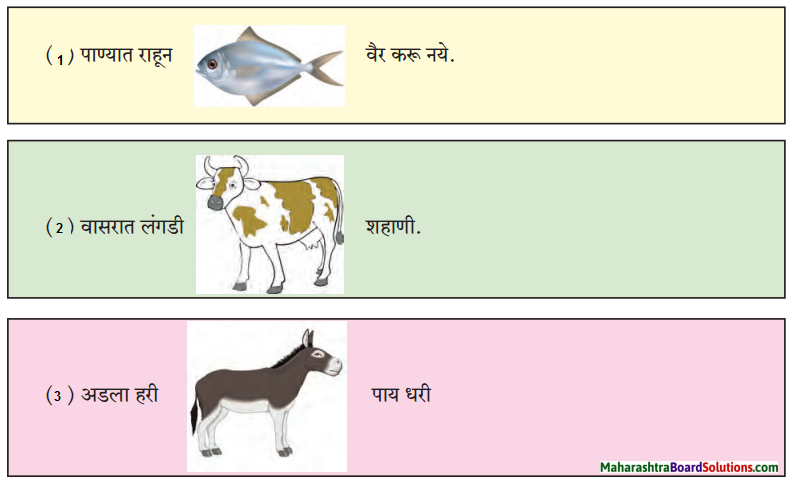
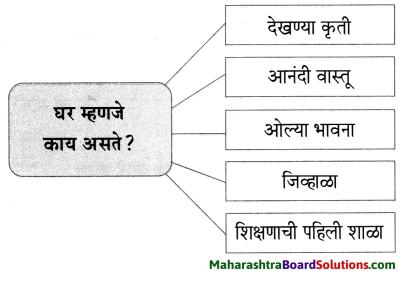
Balbharti Maharashtra State Board Class 6 English Solutions Chapter 4.3 Mr Nobody Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 English Solutions Chapter 4.3 Mr Nobody

Class 6 English Chapter 4.3 Mr Nobody Textbook Questions and Answers

1. Read the poem aloud.

Question 1.
Read the poem aloud.

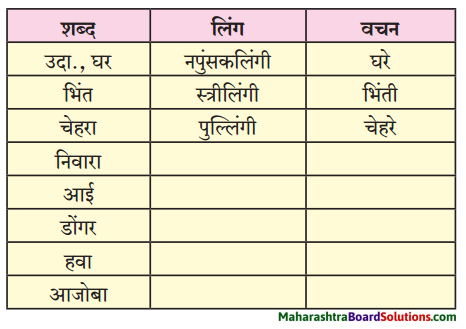
2. Complete the following chart of personal pronouns using words from the brackets.

Question 1.
Complete the following chart of personal pronouns using words from the brackets:
(him, our, we, he, her, their, it, me, your).

Which of the above pronouns do you use when you talk about yourself?
Answer:
I, my, me, us, our, ours

Question 2.
Suppose you are telling someone about the good/bad things they have done. What pronouns are you likely to use?
Answer:
you, your, yours

Question 3.
Suppose you are complaining about one or more persons, things to your teacher/mother. What pronouns will you use?
Answer:
he, she, they, him, her, them, his, here, their’s.

3. Write all the instances of the mischief done by Mr Nobody.

Question 1.
Write all the instances of the mischief done by Mr Nobody.
Answer:

1. Mr Nobody breaks plates by causing cracks in them.
2. He tears books.
3. He leaves the door ajar.
4. He pulls the buttons from our shirts.
5. He scatters the pins afar.
6. He does not oil the door and leaves it squeaking.
7. He leaves finger marks upon the door, as he does not keep his hands clean.
8. He spills the ink.
9. He leaves the boots lying around here and there, without putting them in place.

4. What characteristics of Mr Nobody do we learn about from this poem?

Question 1.
What characteristics of Mr Nobody do we learn about from this poem?
Answer:
Mr Nobody seems to be a very mischievous, playful and irresponsible person. He does not handle things with care as he breaks plates. He behaves in a very careless manner by leaving the door ajar. He seems to be very insensitive to others’ problems because he pulls out buttons from shirts and scatters pins.

5. Imagine that there is a Mr Somebody who has to correct all the wrongs that are done by Mr Nobody.

Question 1.
Write in the following table, what Mr Somebody will have to do.

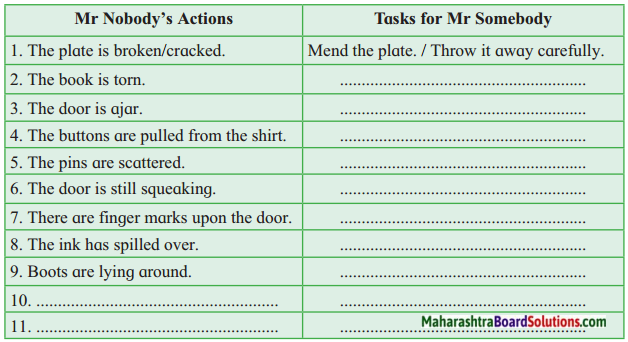
A few more things to the list in the above table, using your own ideas and experience.
Answer:

Mr Nobody’s Actions	Tasks for Mr Somebody
1. The plate is broken/cracked.	Mend the plate./Throw it away carefully.
2. The book is torn.	Mend the book by either sticking a cello tape or any adhesive that is suitable.
3. The door is ajar.	Shut the door properly.
4. The buttons are pulled from the shirt.	Tuck the buttons on the shirt.
5. The pins are scattered.	Gather all the pins, put them in a container and keep them safely in an appropriate place.
6. The door is still squeaking.	Oil the door to prevent it from squeaking.
7. There are finger marks upon the door.	Wipe and clean the finger marks on the door.
8. The ink has spilled over.	Clean and wipe the spilled ink.
9. Boots are lying around.	Arrange the shoes in pairs and put them on the shoe rack neatly.
10. Expensive clothes are scattered.	Gather the clothes and put them in the laundry basket (to be put for washing).
11. Dirty plates on the table	Pick up the plates and glasses and place them in the sink for washing.
12. Leave the comb without cleaning.	Remove the hair from the comb, wipe neatly and keep it in the comb stand.

6. Write about one occasion each when you have behaved like:

Question 1.
Write about one occasion each when you have behaved like:
Answer:
a. Mr Nobody: I took out the thermometer for checking my temperature as I suspected that I was running fever. After checking my body temperature, I kept the thermometer on my bed next to me. My mother who came in to check if I was not keeping too well, sat on it. The thermometer not only broke but also hurt her on her palm.

b. Mr Somebody: My dad came home in a hurry from the bank and was leaving for office. In haste, he forgot his mobile. I spotted it as soon as he left. So, I took and went behind him to give it to him so that he would not miss out on any of his urgent business calls.

7. Listen and complete.

Question 1.
Close your books. The teacher will dictate some lines from the poem. She will say the first half and you have to write the entire line/verse.
(a) I know a funny …….. ………. .
As quite as a ………..
Who does the mischief that is done
………… ………… ………..!

(b) There’s no one ever sees his face,
And yet we all ………….
That every plate we break was ………….
By ………… …………

8. Use the following expressions in your own sentences.

Question a.
We all agree that ……………..
Answer:
We all agree that we should plant at least one tree each year and nurture it to save our environment.

Question b.
It is he/she who …………..
Answer:
It is he/she who helped the blind old lady to cross the road in spite of being in a hurry to reach school.

Question c.
Don’t you see …………….
Answer:
Don’t you see that all lot of effort and hard work has to be put in order to succeed?

Question d.
None of us…
Answer:
None of us ever thought about such an interesting and brilliant idea.

Class 6 English Chapter 4.3 Mr Nobody Additional Important Questions and Answers

Reading Skills and Poetic Device.

Question 1.
Give the description of the man – Mr Nobody.
Answer:
Mr. Nobody is a funny little mischievous man who is as quiet as a mouse.

Question 2.
What does Mr Nobody do?
Answer:
Mr. Nobody does all the mischief that is done in everybody’s house, without being visible to anyone.

Question 3.
What is the fact that all agree about Mr Nobody?
Answer:
All of us agree to it that every plate that we break was cracked by Mr Nobody.

Question 4.
What mischief does Mr Nobody do with books and the door?
Answer:
Mr Nobody always tears out books and leaves the door ajar (slightly open).

Question 5.
What are the things done to our shirts and pins by Mr Nobody?
Answer:
Mr Nobody pulls the buttons from our shirts and scatters the pins far and wide.

Question 6.
What work do we leave undone, to be done by Mr Nobody?
Answer:
We leave the work of oiling the door to be done by Mr. Nobody.

Question 7.
Why is oiling required for the door?
Answer:
Oiling has to be done to the door because it is making the squeaking noise, while opening and closing.

Read the extract and answer the questions given below.

Question 1.
What are the things that we mess up with but blame them as belonging to Mr Nobody? Why?
Answer:
The finger marks on the door, the unclosed blinds that make the curtains fade, the spilled ink, the boots lying around – all these things belong to us, but to avoid being blamed by the others as being irresponsible.

Question 2.
What do we do to the door and not agree that we have done?
Answer:
We leave our finger marks upon the door because our hands are not clean. But we do not agree that we have done so.

Question 3.
How do we make the curtains fade?
Answer:
We never keep the blinds of the windows closed. The sunlight falls on the curtains inside and makes the curtains lose their bright colour. So, the curtains have a faded look.

Question 4.
What happens to the ink and boots sometimes?
Answer:
We spill the ink and allow the boots to be kept in an unorganized manner. The boots are not kept on the shoe rack.

Mr. Nobody Summary in English

The poet begins by stating that there is a funny little person in every house, who does all the mischief very quietly. No one can see this person’s face because he does not let himself become visible as he does everything wrong. Yet, all of us do agree that every plate that was found cracked (mischief done) was done so by Mr. Nobody.

Mr. Nobody is the one who always damages books by tearing them. He leaves the door slightly open without closing it properly. Mr. Nobody also pulls away the buttons from our shirts making them unfit for wearing. He scatters the pins here and there and afar, and makes them invisible to everyone and dangerous too. We let the squeaking door squeak and do not bother to oil it because we leave the work of oiling to be done by Mr. Nobody. We do not want to take pains to do anything responsibly.

We never leave finger marks upon the door. If at all they are there, they are made by none of us. If the blinds are left unclosed, then the curtains start fading. Even if they remain unclosed, we are never to be blamed as we never leave them unclosed. We never spill the ink for all this is done by Mr. Nobody. The books that are lying around are not ours. They belong to Mr. Nobody.

Introduction:

‘Mr. Nobody’ is a poem whose poet is unknown. The poem deals with many things that we never bother about and leave carelessly. This attitude of living very lackadaisical about many everyday things and chores is brought to our notice. The poet also feels that instead of living negligently, we should introspect and exhibit a more responsible behaviour.

Glossary:

1. mischief – troublesome and playful behaviour
2. cracked – broken glitch
3. ajar – slightly open
4. scatters (adv) – throws about and strews
5. afar (adv) – at or to a distance
6. prithee – please (used to convey a polite request) old English of ‘I pray thee’
7. blinds – screens for a window
8. fade – lose colour, freshness or strength gradually.
9. spill – cause to fall or run out of a container

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 17 पाणपोई Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 17 पाणपोई (कविता)

Marathi Sulabhbharti Class 6 Solutions Chapter 17 पाणपोई Textbook Questions and Answers

1. एक – दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
अंगाची लाही लाही कशामुळे होते?
उत्तर:
उन्हामुळे अंगाची लाही लाही होते.

प्रश्न 2.
अवखळ वारा सुटल्यावर काय होते?
उत्तर:
अवखळ वारा सुटल्यावर पालापाचोळा धुळीबरोबर उडतो.

प्रश्न 3.
थकलेल्या वाटसरूला ग्लानी का येते?
उत्तर:
रखरखत्या उन्हामुळे थकलेल्या वाटसरूला ग्लानी येते.

प्रश्न 4.
पाणपोईवर पाणी पिण्यास कोण कोण येतात?
उत्तर:
पाणपोईवर पाणी पिण्यास गरीब श्रीमंत दोन्हीही येतात.

प्रश्न 5.
ज्यांनी पाणपोई थाटली त्याला आशीर्वाद का देतात?
उत्तर:
रखरखत्या उन्हात रांजणातले थंडगार पाणी पिऊन सर्व तृप्त होतात म्हणून त्याला आशीर्वाद देतात.

2. उष्णगरम, थंडगार, पालापाचोळा या शब्दांतील दोन्ही शब्द एकाच अर्थाचे आहेत, असे शब्द शोधा व लिहा.

प्रश्न 1.
उष्णगरम, थंडगार, पालापाचोळा या शब्दांतील दोन्ही शब्द एकाच अर्थाचे आहेत, असे शब्द शोधा व लिहा.

3. घामेजणे, लाहीलाही होणे, उष्णगरम झळाई, रखरखते ऊन, तहान लागणे या शब्दसमुहांचा वापर करून पाच-सहा वाक्ये लिहा.

प्रश्न 1.
घामेजणे, लाहीलाही होणे, उष्णगरम झळाई, रखरखते ऊन, तहान लागणे या शब्दसमुहांचा वापर करून पाच-सहा वाक्ये लिहा.
उत्तर:
उन्हाळ्याचे दिवस होते. रखरखते ऊन होते. मामाच्या शेतावर जायचे होते. अंगाची लाहीलाही होत होती. आम्ही घामेजलो होतो. उष्णगरम झळाई लागत होती. घसा कोरडा पडला होता. तहान लागली होती. जवळच्या झऱ्यातून थंडगार गोड पाणी प्यायलो. मन तृप्त झाले.

4. रखरख, गरगर यांसारखे अक्षरांची पुनरावृत्ती होणारे शब्द शोधा.

प्रश्न 1.
रखरख, गरगर यांसारखे अक्षरांची पुनरावृत्ती होणारे शब्द शोधा.
उत्तर:

1. लाहीलाही
2. सारखीसारखी
3. झरझर
4. भरभर
5. पटपट

5. पाणपोई हा पाण्याशी संबंधित शब्द आहे. तसेच खालील शब्द वाचा व समजून घ्या.

पाणबुड्या, पाणलोट, पाणवठा, पाणथळ, पाणकोंबडा, पाणघोडा, पाणवनस्पती.

6. ऊन या शब्दाला विशेषणे लावलेली आहेत. ती वाचा व समजून घ्या.

7. खालील विरूद्धार्थी शब्द लिहा.

प्रश्न 1.
खालील विरूद्धार्थी शब्द लिहा.
उत्तर:

1. गार × गरम
2. रंक × राव
3. ऊन × सावली
4. तृप्त × अतृप्त
5. दुवा × शाप
6. सज्जन × दुर्जन

8. तुम्हांला खूप तहान लागली असताना अचानक पाणपोई दिसली, तर तुमच्या मनात कोणते विचार येतील ते लिहा.

प्रश्न 1.
तुम्हांला खूप तहान लागली असताना अचानक पाणपोई दिसली, तर तुमच्या मनात कोणते विचार येतील ते लिहा.
उत्तर:
डांबरी रस्त्यावरून चालताना उष्णतेच्या झळा लागत होत्या. थंडगार पाणी प्यावेसे वाटत होते आणि अचानक एक पाणपोई दिसली. माझ्या मनात विचार येतील की ही पाणपोई कोणी ठेवली असेल? त्या सज्जन माणसास मला भेटता येईल का? हे पाणी थंडगार कसे राहते? लाल फडके कोण बांधून जाते? त्या सज्जनाचे मला आभार मानता येतील का? इत्यादी.

9. चालून चालून थकलेल्या वाटसरूला थंडगार पाणी मिळाल्यावर काय वाटत असेल, कल्पना करा व लिहा.

प्रश्न 1.
चालून चालून थकलेल्या वाटसरूला थंडगार पाणी मिळाल्यावर काय वाटत असेल, कल्पना करा व लिहा.
उत्तर:
मे महिन्याची दुपार होती. वाटसरू दुसऱ्या गावाला जायला निघाला. जवळ पाणीही नव्हते. रखरखत्या उन्हात चालवत नव्हते. ग्लानी येत होती. कडक ऊन होते. थोडे पुढे जाऊन पहातो तो काय एका मोठ्या वृक्षाखाली पाणपोई दिसली. मनाला खूप बरे वाटले. ज्यानी कोणी ती पाणपोई ठेवली होती त्याला खूप दुवा दिला. समाजसेवेची ही पद्धत किती न्यारी आहे असे वाटले. तहान शमली. तृप्तता झाली.

10. तुमच्या गावातील एखादया पाणपोईवर जा. तीकोणी काढली, ती काढण्यामागचा उद्देश, त्याची निगा कशी राखतात, पाणी कसे भरले जाते याची माहिती घ्या. ती एक मोठी समाजसेवा कशी आहे, याबद्दल सात-आठ ओळी लिहा.
उत्तर:
राजापूर आमचे गाव. उन्हाळा सुरू झाला की गावातील एक ज्येष्ठ व्यक्ती व त्यांचा तरूण मुलगा मोठ्या झाडाच्या पारावर सुंदर मोठे काळे माठ आणतात. त्यात स्वच्छ गोड पाणी भरतात. त्या माठाला ओले लाल फडके बांधतात. त्यामुळे माठातील पाणी थंडगार रहाते. वाटसरूंना, तहानलेल्यांना एवढ्या प्रचंड उष्णतेत गार पाणी मिळावे व त्यांची तहान शमावी हा त्यामागील उद्देश. वाटसरूने पाणी काढण्यासाठी ठेवलेल्या डावानेच पाणी घ्यायचे हा दंडक असतो.

त्यात उष्टे भांडे किंवा हात बुडवता येत नाही. हे रांजण नीट झाकलेले असते. केरकचरा त्यात जात नाही. गाळलेले नळाचे पाणी यात भरले जाते. ते जंतुविरहीत असते. ‘तहान शमविण्यासाठी’ स्वेच्छेने केलेली ही सेवा म्हणजे समाजसेवेचे एक उत्तम उदाहरण आहे. यातून ‘परोपकार’ हा मुख्य उद्देश दिसून येतो. आपणासही यातून शिकण्यासारखे आहे. घरातील गॅलरीत व खिडकीबाहेर पक्ष्यांनाही दाणा पाण्याची सोय करता येते. करून तर पहा!

विचार करून सांगा !

प्रश्न 1.
पाराची वाडी या गावातील मुलांनी केलेल्या उपक्रमाबद्दल तुमचे मत सांगा.

प्रश्न 2.
आपण एखादी गोष्ट किंवा उपक्रम करतो, तेव्हा घरातील मोठ्या माणसांना सांगणे आवश्यक आहे का? तुमचे मत सांगा.
उत्तरः
कोणताही उपक्रम हा समाजाच्या हितासाठी असेल तर घरातील मोठ्या माणसांना निश्चितच आनंद होतो. ते देखील तुमची योजना राबवण्यासाठी पुढाकार घेतात. कमी खर्चात योग्य काम कसे होईल हे शिकवितात. त्यासाठी लागणारी शिस्त, नियोजनाचे धडे देतात. म्हणून मोठया माणसांना सांगणे आवश्यक आहे असे मला वाटतेय.

प्रश्न 3.
अशा प्रकारचे कोणकोणते सामाजिक उपक्रम करावे असे तुम्हांला वाटते? ते उपक्रम थोडक्यात सांगा.

प्रश्न 4.
‘पाणी’ या विषयावरची घोषवाक्ये तयार करून त्याच्या पाट्या तयार करा.
उत्तर:

प्रश्न 5.
‘पाणी हेच जीवन’ यांवर आधारित दहा ओळी लिहा.

प्रश्न 6.
तुम्ही एखादा उपक्रम केला असेल, तर त्याबाबतची माहिती मित्राला पत्राने कळवा.

प्रश्न 7.
खालील उतारा वाचा. त्या उताऱ्यात पूर्णविराम (.) स्वल्पविराम (,) प्रश्नचिन्ह (?) उद्गारचिन्ह (!) आणि एकेरी अवतरणचिन्ह (‘-‘) घाला व उतारा पुन्हा लिहा.

प्रश्न 8.
इयत्ता पाचवीमध्ये तुमचा शब्दसंग्रह तुम्ही तयार केला आहे. शब्दसंग्रह किंवा शब्दकोश कसा पाहावा हे आपण पाहूया.

प्रश्न 9.
वर दिलेले ‘अ’ गटातील व ‘ब’ गटातील शब्द वाचा.
‘अ’ गटातील शब्द हे बाराखडीतील स्वरचिन्हानुसार दिलेले नाहीत.
मात्र ‘ब’ गटातील शब्द हे बाराखडीतील स्वरचिन्हानुसार दिलेले आहेत.

प्रश्न 10.
पाठ्यपुस्तकातील पाठ 2 आणि पाठ 3 मधील शब्दार्थ खालील चौकटीत दिले आहेत.

प्रश्न 11.
पाठ्यपुस्तकातील पाठ 2 आणि पाठ 3 मधील शब्दार्थ शब्दकोशाप्रमाणे खालील चौकटीत दिले आहेत.

‘अ’ गट

लुकलुकणे-चमकणे.
तल्लीन होणे-दंग होणे, गुंग होणे.
कडकडून भेटणे-प्रेमाने मिठी मारणे.
बिलगणे-प्रेमाने जवळ येणे.
गहिवरून येणे-मन भरून येणे.
धमाल-मजा.
पाडाचा आंबा-अर्धवट पिकलेला आंबा.
आमराई-आंब्याच्या झाडांची बाग.
ऐन दुपारी- भर दुपारी.
भणाण वारा – वाऱ्याचा भयभीत करणारा आवाज.
खचणे-खाली खाली जाणे, ढासळणे.
चडफड- राग,
गिल्ला करणे-गोंधळ करणे.

‘ब’ गट

आमराई-आंब्याच्या झाडांची बाग,
ऐन दुपारी- भर दुपारी.
कडकडून भेटणे-प्रेमाने मिठी मारणे.
खचणे- खाली खाली येणे, ढासळणे.
गहिवरून येणे-मन भरून येणे.
गिल्ला करणे-गोंधळ करणे.
चडफड- राग.
तल्लीन होणे-दंग होणे, गुंग होणे.
धमाल-मजा.
पाडाचा आंबा-अर्धवट पिकलेला आंबा.
बिलगणे-प्रेमाने जवळ येणे.
भणाण वारा – वाऱ्याचा भयभीत करणारा आवाज.
लुकलुकणे-चमकणे.

आले का लक्षात?

‘क, ख ….. ज्ञ’ या अक्षरांच्या क्रमानुसार व बाराखडीतील चिन्हानुसार वरील शब्द लिहिले आहेत. शब्दकोश पाहताना याच पद्धतीने पाहा. पाठ्यपुस्तकातील किंवा पाठ्येतर साहित्यातील शब्दांचे अर्थ पाहताना या पद्धतीने शब्दकोश पाहा. पाठ्यपुस्तकातील इतर पाठांमध्ये आलेले शब्दार्थ पाहा व शब्दकोशाप्रमाणे लिहून अधिकचा सराव करा.

Class 6 Marathi Chapter 17 पाणपोई Additional Important Questions and Answers

योग्य पर्याय निवडून उत्तरे लिहा.

प्रश्न 1.
उन्हाने अंगाची ……………. होते. (लाहीलाही / आग)
उत्तर:
लाहीलाही

प्रश्न 2.
…………….. सावलीत पाणपोई थाटली आहे. (आंब्याच्या / वटवृक्षाच्या)
उत्तर:
वटवृक्षाच्या

प्रश्न 3.
रखरखत्या उन्हात …………….. वारा सुटला आहे. (उष्णगरम / अवखळ)
उत्तर:
अवखळ

प्रश्न 4.
पाणी पिण्यास ……………… ठेवतात. (रांजण / माठ)
उत्तर:
रांजण

प्रश्न 5.
पाणी पिऊन ………………. दुवा देतात. (लोकांना / सज्जनास)
उत्तर:
सज्जनास

खालील प्रश्नांची एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
रांजण कसे होते?
उत्तर:
रांजण गार पाण्याने भरलेले व लाल कापडाने झाकलेले होते.

प्रश्न 2.
कवितेच्या खालील ओळी पूर्ण करा.
उत्तर:

1. ……………. होतीया लाहीलाही.
2. आठवते दग्ध ………………….
3. …………………. अवखळ वारा.
4. …………………. उंच अंबरा.
5. …………………. मोठी तहान.
6. ‘रंक असो ………………….
7. धन्य असो ………………….
8. पिऊनीया ………………….

उत्तरः

1. उन्हात घामेजुनी अंगाची होतीया लाहीलाही.
2. आठवते दग्ध उन्हातली थंडगार सराई.
3. रखरखत्या उन्हात सुटतो अवखळ वारा.
4. धुळीसंगे पालापाचोळा जाई या उंच अंबरा.
5. सारखीसारखी लागते साऱ्यांना मोठी तहान.
6. ‘रंक असो वा राव,’ हे पाणी पितात सारेजण!
7. धन्य असो ज्याने थाटिली ही पाणपोई उन्हात.
8. पिऊनीया पाणी दुवा देती सारे त्या सज्जनास.

व्याकरण व भाषाभ्यास

विशेषण:
नामाबद्दल अधिक माहिती सांगणाऱ्या शब्दास विशेषण म्हणतात.
उदा. सुंदर, कोवळे, लहान, लुसलुशीत, कडक, गोजिरवाणे इ.

प्रश्न 1.
जोड्या जुळवा.

नाम	विशेषण
1. ताजमहाल	अ. नरम
2. वारा	ब. थंडगार
3. बर्फ	क. कडक
4. लाकूड	ड. सोसाट्याचा
5. कापूस	इ. सुंदर

उत्तर:

नाम	विशेषण
1. ताजमहाल	इ. सुंदर
2. वारा	ड. सोसाट्याचा
3. बर्फ	ब. थंडगार
4. लाकूड	क. कडक
5. कापूस	अ. नरम

प्रश्न 2.
‘वारा’ या शब्दाला विशेषणे लावा..
उत्तर:

प्रश्न 3.
एकाच अर्थाचे शब्द शोधा. जसे की – उष्णगरम, थंडगार, पालापाचोळा.
उत्तर:

1. केरकचरा
2. गोरागोमटा
3. गरमागरम
4. घनदाट
5. काळाकभिन्न

प्रश्न 4.
संबंधित शब्द लिहा.
उत्तर:

1. पाणपोई – पाणबुड्या, पाणबोट, पाणवठा, पाणथळ, पाणकोंबडा, पाणघोडा, पाणवनस्पती
2. जलचर – जलविद्युत, जलसाठा, जलसमाधी, जलाशय, जलसंपत्ती, जलधी

प्रश्न 6.
खालील विरूद्धार्थी शब्द लिहा.
उत्तर:

1. थाटणे × मोडणे
2. आठवणे × विसरणे
3. थकलेला × ताजातवाना
4. मोठी × लहान
5. भरलेले × रिकामे
6. झाकणे × उघडणे

खालील वाक्प्रचारांचा अर्थ सांगून वाक्यात उपयोग करा.

प्रश्न 1.
अंगाची लाहीलाही होणे – उन्हामुळे अंगाची आग होणे.
उत्तर:
वैशाख महिन्यात अंगाची लाहीलाही होते.

प्रश्न 2.
तृप्त होणे – समाधानी होणे.
उत्तर:
भुकेलेला भिकारी भाजीभाकरी खाऊन तृप्त झाला.

विचार करून सांगा !

प्रश्न 1.
कोणकोणते सामाजिक उपक्रम करावेत असे तुम्हांला वाटते? ते उपक्रम थोडक्यात सांगा.
उत्तरः
1. जलसाक्षरता अभियान राबवणे – पाणी ही निसर्गाची अमूल्य देणगी आहे. पाण्याचा योग्य वापर करणे ही प्रत्येकाची जबाबदारी आहे. पाण्याचे सिंचन, नियोजन, वापर अतिशय काळजीपूर्वक करण्यासाठी खेडोपाडी, शहरातून जलसाक्षरता शिबीरे घ्यायला हवी.

2. तंत्रज्ञान साक्षरता – आजच्या तंत्रज्ञान आणि माहितीच्या युगात दररोज नवनवीन बदल घडत आहेत. त्याला सामोरे
जाण्यासाठी संगणक, टॅब, मोबाईलची ओळख व त्यात कौशल्य प्राप्त करून घेण्यासाठी वृद्धांचे व जिज्ञासूंचे तंत्रज्ञान साक्षरता वर्ग मोफत घेतले पाहिजे. त्यामुळे संभाव्य अडचणींवर ते मात करू शकतील. उदा. रांगेत उभे न राहता एखादया वृद्ध व्यक्तिला ऑनलाईन बुकींग कसे करतात ते शिकविणे.

पाणपोई Summary in Marathi

काव्यपरिचयः
‘पाणपोई’ या कवितेत उन्हात अंगाची लाहीलाही होत असताना, रखरखते ऊन असताना वाटसरूंना ग्लानी येते व पाणी हवेहवेसे वाटते. तर त्या ठिकाणी स्वच्छ, थंडगार पाणी प्यायला मिळाले तर अत्यंत तृप्तता मिळते. वाटसरूंना पाणी पिण्यासाठी केलेली सोय म्हणजेच पाणपोई. भूतदयेचे हे उत्तम उदाहरण आहे.

शब्दार्थ:

1. दग्ध ऊन – भाजणारे ऊन (burning heat)
2. वाटवृक्ष – वडाचे झाड (Banyan tree)
3. पाणपोई – उन्हाळ्यामध्ये वाटसरूंसाठी केलेली पिण्याच्या पाण्याची सोय (stand to supply water to travellers)
4. अवखळ – खोडकर (naughty, mischevous)
5. थकलेला – दमलेला (tired)
6. ग्लानी – चक्कर, सुस्ती (ennui, fatigue)
7. रांजण – मोठे माठ (big earthen pot)
8. तृप्त – संतुष्ट (satisfied)
9. रंक – गरीब (poor)
10. राव – श्रीमंत (rich)

वाक्प्रचार व अर्थ:

1. अंगाची लाही लाही होणे – उन्हामुळे अंगाची आग होणे.
2. तृप्त होणे – समाधानी होणे.

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 9 घर Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 9 घर (कविता)

Marathi Sulabhbharti Class 6 Solutions Chapter 9 घर Textbook Questions and Answers

1. एक – दोन वाक्यात उत्तरे लिहा.

प्रश्न अ
माणसाची पहिली शाळा कुठे सुरू होते?
उत्तर:
माणसाची पहिली शाळा घरात सुरू होते.

प्रश्न आ
घराने कोणत्या गोष्टी जवळ कराव्यात?
उत्तर:
घराने नवी मूल्ये व नवीन ज्ञान जवळ करावे.

प्रश्न इ
आईच्या हातचे जेवण कसे असते?
उत्तर:
आईच्या हातचे जेवण चविष्ट असते.

2. कवीने घराचे वर्णन कोणत्या शब्दांत केले आहे ते लिहा. 

प्रश्न 1.
कवीने घराचे वर्णन कोणत्या शब्दांत केले आहे ते लिहा.
उत्तर:
घर म्हणजे नुसते दगड, विटा, सिमेंटपासून बनवलेल्या चार भिंतीने तयार केलेली वस्तू नसून ती एक सुंदर कलाकृती असते. ती एक आनंदी वास्तू असते. घरात फक्त वेगवेगळ्या खोल्या असून चालत नाही तर घर म्हणजे जिव्हाळा व प्रेमाने भरलेल्या ओल्या भावना असते. घरातच आपण शिक्षणाच्या पहिल्या शाळेत शिकत असतो. घर म्हणजे फक्त पसारा किंवा केवळ निवारा नसून त्याला स्वत:चा असा एक चेहरा व कहाणी असते. घराला स्वत:ची अशी एक ओळख असते.

घरापासूनच आपण पाहायला, चालायला, धावायला, लढायला व दुःखाचे डोंगर चढायला शिकतो. घराने सतत सावधान व समाधानी असावे. घराने सतत काळाचे भान ठेवावे. त्याने नवीन-नवीन मूल्य स्विकारावीत व नवीननवीन ज्ञान आत्मसात करावे. घरात आई अपार कष्ट करत असते. आजी सतत घरातल्या लहानग्या मुलांना गोष्टी सांगते तर आजोबा सतत सर्वांशी गप्पा मारत असतात. घरी आई जे सर्वांसाठी जेवण बनविते ते अतिशय चविष्ट व रूचकर असते. अशा प्रकारे कवी ‘धुंडिराज जोशी’ यांनी घराचे वर्णन केले आहे.

3. खालील आकृती पूर्ण करा.

प्रश्न 1.
खालील आकृती पूर्ण करा.

उत्तर:

3. शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधून लिहा. 

वस्तू, खोल्या, जिव्हाळा, पसारा, पाहायला, सावधान, भान, गोष्ट, चविष्ट

प्रश्न 1.
शब्दातील शेवटचे अक्षर सारखे येणारे शब्द कवितेतून शोधून लिहा.
वस्तू, खोल्या, जिव्हाळा, पसारा, पाहायला, सावधान, भान, गोष्ट, चविष्ट
उत्तर:

1. वस्तू – वास्तू
2. खोल्या – ओल्या
3. जिव्हाळा – शाळा
4. पसारा – निवारा
5. पाहायला – चालायला
6. लढायला – चढायला
7. सावधान – समाधान
8. भान – ज्ञान
9. गोष्ट – कष्ट
10. चविष्ट – गप्पिष्ट

4. योग्य पर्याय निवडून लिहा.

प्रश्न अ.
घरात हव्या भावना ओल्या – म्हणजे
(अ) घरातील व्यक्तींनी रडावे
(आ) घरातील व्यक्तींनी परस्परांवर प्रेम करावे.
(इ) घरातील व्यक्तीत एक व्यक्ती भावना नावाची असावी.
उत्तर:
(आ) घरातील व्यक्तींनी परस्परांवर प्रेम करावे.

प्रश्न ब.
घर शिक्षणाची पहिली शाळा – म्हणजे
(अ) घरामध्ये बालमंदिर भरते.
(आ) घरापासून शिक्षणाला सुरूवात होते.
(इ) घराच्या शाळेत नाव घातले जाते.
उत्तर:
(आ) घरापासून शिक्षणाला सुरूवात होते.

प्रश्न क.
जवळ करावीत नवी मूल्ये नवीन ज्ञान – म्हणजे
(अ) नवी मूल्ये व नवीन ज्ञानाच्या जवळ राहायला जावे.
(आ) रोज नवीन मूल्यांची व ज्ञानाची पुस्तके वाचावीत.
(इ) काळानुसार मूल्य व ज्ञानातील बदल स्वीकारावे.
उत्तर:
(आ) रोज नवीन मूल्यांची व ज्ञानाची पुस्तके वाचावीत.

5. तुमच्या परिसरातील घराला दिलेली नावे पाहा. यादी करा. 

प्रश्न 1.
तुमच्या परिसरातील घराला दिलेली नावे पाहा. यादी करा.
उत्तर:

1. मातृछाया
2. गोकुळधाम
3. शांतीनिवास
4. कृष्णकुंज
5. गीताई
6. ग्रीनव्हिला
7. दिपांजली
8. शिवसदन
9. राधाकृष्णनिवास
10. मातोश्री
11. सह्याद्री व्हिला
12. मनःस्मृती
13. केशवधाम
14. शांतनुनिवास
15. वृंदावन
16. उत्कर्ष

6. खालील शब्द व त्यांचे अर्थ लक्षात ठेवा.

प्रश्न 1.
खालील शब्द व त्यांचे अर्थ लक्षात ठेवा.
उत्तर:

1. चविष्ट – चव असणारे
2. विशिष्ट – ठरावीक प्रकारचा
3. भ्रमिष्ट – भ्रम झालेला
4. गप्पिष्ट – गप्पा मारणारा
5. कोपिष्ट – रागावलेला
6. अनिष्ट – योग्य नसलेले

7. खालील शब्दांचे लिंग ओळखा व वचन बदला. 

प्रश्न 1.
खालील शब्दांचे लिंग ओळखा व वचन बदला.

उत्तर:

शब्द	लिंग	वचन
1. घर	नपुंसकलिंगी	घरे
2. भिंत	स्त्रीलिंगी	भिंती
3. चेहरा	पुल्लिंगी	चेहरे
4. निवारा	पुल्लिंगी	निवारे
5. आई	स्त्रीलिंगी	आया
6. डोंगर	पुल्लिंगी	डोंगर
7. हवा	स्त्रीलिंगी	हवा
8. आजोबा	नपुंसकलिंगी	आजोबा

8. खालील शब्द शिक्षकांच्या मदतीने समजून घ्या.

9. खालील शब्द वाचा लिहा.

10. वस्तू आणि वास्तू या दोन शब्दांतील लेखनामध्ये फक्त ‘काना’ दिल्याने फरक पडतो; परंतु अर्थामध्ये खूप फरक आहे. खाली दिलेल्या शब्दांचे अर्थ शोधा. लिहा. उदा., वस्तू – जिन्नस, नग वास्तू – घर
कप – काप, तार – तारा, खरे – खारे, गर – गार, घर – घार, चार – चारा, पर – पार, वर – वार

प्रश्न 1.
कप – काप
उत्तर:

प्रश्न 2.
तार – तारा
उत्तर:

प्रश्न 3.
खरे – खारे
उत्तर:

प्रश्न 4.
गर – गार
उत्तर:

प्रश्न 5.
घर – घार
उत्तर:

प्रश्न 6.
चार – चारा
उत्तर:

प्रश्न 7.
पर – पार
उत्तर:

प्रश्न 8.
वर – वार
उत्तर:

11. तुमच्या घराचे चित्र काढून रंगवा व त्यांचे सहा सात वाक्यांत वर्णन करा. 

प्रश्न अ.
तुमच्या घराचे चित्र काढून रंगवा व त्यांचे सहा सात वाक्यांत वर्णन करा.
उत्तर:
माझ्या घराचे नाव ‘गोकुळधाम’ आहे. माझ्या घरात मी, माझे आई-बाबा व मोठी ताई असे चार जण राहतो. माझी आई घरातील सर्व कामे करते. माझे बाबा शेताची सर्व कामे करतात. मी व ताई आम्ही रोज शाळेत जातो व अभ्यास करतो. माझ्या घराभोवती विविध प्रकारची झाडे आहेत. माझ्या घरासमोरून एक नदी वाहते. तिचे पाणी स्वच्छ व चवदार आहे. माझे घर म्हणजे फक्त दगड व माती पासून बनवलेल्या भिंती नसून त्यात एक प्रकारचा जिव्हाळा आहे.

प्रश्न आ.
चित्राच्या जागी योग्य शब्दाचा वापर करून खालील म्हणी पूर्ण करा.

उत्तर:

प्रश्न 1.

उत्तरः
पाण्यात राहून माशाशी वैर करू नये,

प्रश्न 2.

उत्तर:
वासरात लंगडी गाय शहाणी.

प्रश्न 3.

उत्तर:
अडला हरी गाढवाचे पाय धरी.

प्रश्न इ.
खालील चित्रांच्या सहसंबंध लावून गोष्ट तयार करा.

उत्तर:
काही मुले स्वच्छंदी मनाची असतात. माझे मनही तसेच आहे. मी एके दिवशी क्रिकेटचे सामान घेऊन मोकळ्या माळरानावर खेळायला गेलो होतो. तिथे गेल्यावर मी काही फुलपाखरे पाहिली. ती त्या माळावर स्वच्छंदी उडत होती. बागडत होती. त्यांच्या पंखावरील विविध रंग पाहून मी आश्चर्यचकितच झालो. निसर्ग ही रंगांची किमया कशी साधतो ते मला कळेना. त्याच मोकळ्या माळावर काही मुले पतंग उडवताना दिसली. त्यांचे त्या पतंगांचे विविध रंग पाहून मलाही पतंग उडवण्याचा मोह झाला आणि मी क्रिकेट सोडून पतंग उडवण्यात गुंग झालो.

Marathi Sulabhbharti Class 6 Solutions Chapter 9 घर Important Additional Questions and Answers

खालील पदयपंक्तींच्या रिकाम्या जागा भरून ओळी पूर्ण करा.

प्रश्न 1.

1. घर नाही चार …………….. घर असते देखण्या ……………..
2. घर नाही एक……………… .घर म्हणजे आनंदी …………….. .
3. घर नाही नुसत्या ……………. घरात हव्या भावना …………….. .
4. घरात हवा ………………., घर शिक्षणाची पहिली …………….. .
5. घर नाही पसारा, घर नाही ………………… निवारा.
6. घराला असते …………….., घराला असतो आपला .
7. घराने असावे …………….. घराने द्यावे …………….. .
8. घराने ठेवावे …………….. भान, जवळ करावीत नवी …………….. नवीन ……………….
9. घरात आईचे अपार …………….. ,आजी सांगते ……………… गोष्ट,
10. घरात आजोबा …………….. , आईच्या हातचे जेवण …………….. .

उत्तर:

1. भिंती, कृती
2. वस्तू, वास्तू
3. खोल्या, ओल्या
4. जिव्हाळा, शाळा
5. नुसता, केवळ
6. कहाणी, चेहरा
7. सावधान, समाधान
8. काळाचे, मूल्ये, ज्ञान
9. कष्ट, सुंदर
10. गप्पिष्ट, चविष्ट

खालील प्रश्नांची एक ते दोन वाक्यात उत्तरे लिहा.

प्रश्न 1.
घर कसल्या कृती असते?
उत्तर:
घर देखण्या कृती असते.

प्रश्न 2.
घर म्हणजे कशी वास्तू असते?
उत्तर:
घर म्हणजे आनंदी वास्तू असते..

प्रश्न 3.
घरात कशा भावना हव्यात?
उत्तर:
घरात ओल्या भावना हव्यात.

प्रश्न 4.
घराला स्वत:चा असा काय असतो?
उत्तर:
घराला स्वत:चा असा आपला चेहरा असतो.

प्रश्न 5.
घर काय काय शिकवते?
उत्तर:
घर पाहायला, चालायला, धावायला, लढायला, दुःखाचा डोंगर चढायला शिकवते.

प्रश्न 7.
घराने कशाचे भान ठेवावे?
उत्तर:
घराने काळाचे भान ठेवावे.

प्रश्न 8.
घरात अपार कष्ट कोण करते?
उत्तर:
घरात अपार कष्ट आई करते.

प्रश्न 9.
घरात सुंदर गोष्ट कोण सांगते?
उत्तर:
घरात सुंदर गोष्ट आजी सांगते.

प्रश्न 10.
घरात गप्पा करणारे कोण आहेत?
उत्तर:
घरात आजोबा गप्पा करणारे आहेत.

व्याकरण व भाषाभ्यास

प्रश्न 1.
समानार्थी शब्द लिहा.

1. घर
2. जिव्हाळा
3. पहिली
4. शाळा
5. कहाणी
6. चेहरा
7. डोंगर
8. काळ
9. मूल्ये
10. कष्ट ङ्के

उत्तर:

1. सदन, पास्त, निवास
2. प्रेम
3. प्रथम
4. विद्यालय
5. गोष्ट, कथा
6. तोंड, वदन
7. पर्वत
8. वेळ
9. आदर्श
10. परिश्रम

प्रश्न 5.
विरूद्धार्थी शब्द लिहा.

1. देखणा
2. एक
3. आनंद
4. ओल्या
5. जिव्हाळा
6. पहिली
7. असते
8. ज्ञान
9. सुंदर
10. आजी
11. जवळ

उत्तर:

1. विद्रुप
2. अनेक
3. दु:ख
4. सुक्या
5. द्वेष, मत्सर
6. शेवटची
7. नसते
8. अज्ञान
9. कुरूप
10. आजोबा
11. दूर

प्रश्न 6.
खालील शब्दांचे वचन बदला,

1. घर
2. भिंत
3. खोली
4. ओली
5. शाळा
6. निवारा
7. कहाणी
8. चेहरा
9. मूल्य
10. गोष्ट

उत्तर:

1. घरे
2. भिंती
3. खोल्या
4. ओल्या
5. शाळा
6. निवारे
7. कहाण्या
8. चेहरे
9. मूल्ये
10. गोष्टी

प्रश्न 2.
खालील वेब पूर्ण करा.
उत्तर:
1.

2.

खालील शब्द व त्यांचे अर्थ लक्षात ठेवा.

प्रश्न 1.
खालील शब्द व त्यांचे अर्थ लक्षात ठेवा.
उत्तर:

1. नादिष्ट – छंद असणारा
2. गर्विष्ट – गर्व असणारा
3. कनिष्ट – लहान असणारा
4. वरिष्ट – मोठा असणारा
5. इष्ट – चांगले

चित्राच्या जागी योग्य शब्दाचा वापर करून खालील म्हणी पूर्ण करा.

प्रश्न 1.

उत्तरः
हातच्या कंकणाला आरसा कशाला.

प्रश्न 2.
नाकापेक्षा जड
उत्तर:
नाकापेक्षा मोती जड.

घर Summary in Marathi

काव्य परिचयः

‘घर’ या कवितेत धुंडिराज जोशी यांना घर म्हणजे केवळ चार भिंती नसून त्यापलिकडेही बरेच काही असल्याचा विचार मांडला आहे. घर एक आनंदी वास्तू असून त्या घराशी जिव्हाळा, अनके भावना निगडित असतात. हे घरच आपल्याला अनेक गोष्टी शिकवते, आपल्याला समाधान देते. याच घरात आजी, आजोबा या सगळ्यांच्या आठवणीदेखील सामावलेल्या असतात. घरासंबंधीचे फार सुंदर विचार या कवितेत मांडले आहेत.

शब्दार्थ:

1. घर – निवास, निवारा (house)
2. भिंत – तट (wall)
3. देखण्या – सुंदर (beautiful)
4. कृती – काम (work)
5. वस्तू – (things)
6. वास्तू – इमारत (building)
7. नुसत्या – फक्त, केवळ (only)
8. खोली – (room)
9. हव्या – पाहिजेत (want)
10. ओल्या भावना – प्रेमळ भावना (loving feelings)
11. जिव्हाळा – आत्मीयता (attachment)
12. पहिली – प्रथम (first)
13. शाळा – विद्यालय (school)
14. नुसता – फक्त, केवळ (only)
15. निवारा – आसरा (shelter)
16. कहाणी – गोष्ट, कथा (story)
17. चेहरा – मुखवटा, तोंड (face)
18. डोंगर – पर्वत (mountain)
19. चढायला – (toclimb)
20. सावधान – जागृत (to alert, vigilant)
21. ठेवावे – मांडणे (to keep)
22. काळ – समय (period, time)
23. भान – जाणीव (consciousnest)
24. नवी – नवीन (new)
25. मूल्ये – किंमत (value)
26. ज्ञान – माहिती (knowledge)
27. अपार – खूप, जास्त (to much)
28. कष्ट – परिश्रम (hard work)
29. आजी – (grandmother)
30. सुंदर – छान (lovely)
31. आजोबा – (grandfather)
32. सांगते – (to tell) बोलणे
33. गप्पिष्ट – गप्पा करणारे (talkative, chatter)
34. चविष्ट – रूचकर, चवदार (tasty, delicious)

Balbharti Maharashtra State Board Class 6 English Solutions Chapter 2.1 The Clothesline Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 English Solutions Chapter 2.1 The Clothesline

Class 6 English Chapter 2.1 The Clothesline Textbook Questions and Answers

1. Read the poem aloud. Recite any stanza of your choice from memory.

Question 1.
Read the poem aloud. Recite any stanza of your choice from memory.

2. Answer the following questions with reference to the poem.

Question a.
What is described in the poem?
Answer:
The poetess Charlotte Druitt Cole describes the clothes on the clothesline swaying in the wind, waiting to be free.

Question b.
What are the clothes compared to? Give two examples.
Answer:
The clothes are compared to white snow, restive horses, fairy-tale witches, a bird and a sail.

Question c.
What do restive horses do?
Answer:
Restive horses are unable to remain still; dance in a lively, playful manner and walk or move with high springy steps.
OR
Restive horses caper and prance

Question d.
What do fairy-tale witches do?
Answer:
Fairy-tale, witches dance wildly in a very hard and violent manner.

Question e.
What did one of the fluttering creatures do?
Answer:
One of the fluttering creatures freed herself from the clutches of the pegs, and soared high into the air like a bird and made it difficult for anyone to find her.

Question f.
What could have happened to the one who flew away? Who was she?
Answer:
The one who flew away happened to be the poetess’ handkerchief. She could be hidden somewhere in a ditch or drowned in the sea.

3. Form groups and discuss the following questions:

Question a.
Why are clothes compared to living things?
Answer:
The clothes are compared to living things, as they feel they need to be free from any kind of bondage just like living things.

Question b.
The events described in the poem take place at a certain place, at a certain period of the year, under specific weather conditions. Describe the place, the time and the weather conditions.
Answer:
The events described may be taking place in the backyard of a household, during the spring season, whilst the warm air in the afternoon makes the weather seem warmer than usual.

4. When we say that two or more words rhyme, we mean that they end with the same sound or syllable. For example, ‘ring – sing’. Rhyming words are often used in the verse at the end of the lines. List the rhyming words from the poem. Note the words ‘behind’ and ‘wind’. They have similar spellings, that is they look the same. But they are pronounced differently, that is, they do not ‘sound’ the same. This is known as ‘eye rhyme’. Separate the examples of eye rhymes from the following list.
Answer:

Rhyming Words	Eye Rhyme words
cry- try	none – shone
stronger – longer	shut – put
laughter – daughter	imply – simply
won – done
known – grown
beat – feat

5. List all the phrases from the poem in which two or more words are joined with ‘and’.

Question 1.
List all the phrases from the poem in which two or more words are joined with ‘and’.
Answer:

1. hither and thither
2. caper and prance
3. shiver and skip
4. flipping and flapping and flopping

6. Form groups and discuss what must have happened to the handkerchief. Write the story in your own words.

Question 1.
Form groups and discuss what must have happened to the handkerchief. Write the story in your own words.
Answer:
Wash your handkerchief clean. Hang it with a peg to dry in the wind. Watch how it flutters.

7. Wash your handkerchief clean. Hang it with a peg to dry in the wind. Watch how it flutters.

Question 1.
Wash your handkerchief clean. Hang it with a peg to dry in the wind. Watch how it flutters.

8. Complete the following comparisons.
as white us ………………….
as green as ………………….
us red as ………………….
as blue as ………………….
us black as ………………….
as bright as ………………….

Question a.
Rewrite these comparisons using the comparative degree.
Example: Whiter than snow
Answer:

• Bluer than sky
• Blacker than coal.
• Redder than blood.

Question b.
Find suitable objects for each comparison.
Example: Petals or flowers or feathers whiter than snow.
Answer:

• Ocean or eyes bluer than sky.
• Leaves or moss greener than grass.
• Crow or night blacker than coal.
• Sapphire or rose redder than blood.
• Stars or light brighter than sun.

Class 6 English Chapter 2.1 The Clothesline Additional Important Questions and Answers

Reading Skills and Poetic Device

Read the following extract and answer the questions given below.

Question 1.
How do the clothes on the clothesline dance?
Answer:
The clothes on the clothesline dance hand-in-hand in a row, hither and thither, and to and fro.

Question 2.
How do they go?
Answer:
They go flipping, flopping and flapping away.

Question 3.
What are the clothes on the clothesline compared to?
Answer:
The clothes on the clothesline are compared to fluttering creatures that are as white as snow.

Question 4.
What do they do in the merry March wind?
Answer:
The clothes on the clothesline shiver and skip in the merry March wind.

Question 5.
Pick out the rhyming words from the 1st stanza.
Answer:
The rhyming words are ‘row-fro-go-snow’.

Question 6.
Pick out the eye rhyme pair from the 2nd stanza.
Answer:
The pair of eye rhyme in the 2nd stanza is ‘behind-wind’.

Read the following extract and answer the questions given below.

Question 1.
How was she struggling? Why?
Answer:
She was struggling wildly to be free.

Question 2.
Whom did she leave behind?
Answer:
She left pegs and clothesline behind.

Question 3.
How did she fly?
Answer:
She flew like a bird.

Question 4.
What did she gleam like?
Answer:
She gleamed like a sail in the sun.

Question 5.
What was she doing for fun?
Answer:
She was flipping and flopping and flapping for fun.

Question 6.
Where could she now be?
Answer:
She could now be hidden in a ditch or drowned in the sea.

Question 7.
What does the poetess know?
Answer:
The poetess knows for a fact that her handkerchief won’t ever come back to her pocket.

Question 8.
Pick out the rhyming words from the 2nd stanza.
Answer:
The rhyming words are : sun – fun; be – sea.

The Clothesline Summary in English

Paraphrase:

The white clothes that are hung on the clotheslines seem to be dancing in a carefree manner. The clothes’ movements resemble restless horses and their dance reminds the poetess of the wild dance of witches in fairy tales when they dance in the March wind. The poet claims to have seen her handkerchief struggling to be free of the pegs, thereby freeing herself and flying out of reach, like a bird.

The poetess saw her handkerchief flying away merrily. The handkerchief could now be somewhere hiding in a ditch or drowned in the sea. The poetess feels sad about the handkerchief leaving her, knowing very well that she won’t return.

Introduction:

The poetess Charlotte Druitt speaks about the clothes, flapping and blowing on the clothesline on a windy day. She mentions about her handkerchief which left the pegs, gleaming like a sail in the sun and no one could find her.

Glossary:

1. ditch – a trench
2. gleam – a small shaft, stream of light
3. sail – a piece of cloth attached to the mast of a boat to catch the wind and propel it.

Balbharti Maharashtra State Board Class 6 English Solutions Chapter 3.3 Stone Soup Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 English Solutions Chapter 3.3 Stone Soup

Class 6 English Chapter 3.3 Stone Soup Textbook Questions and Answers

1. Answer the following questions.

Question a.
Where does the story take place?
Answer:
The story takes place in a village.

Question b.
List the characters in the play and write one or two lines about each.
Answer:
1. Motiram – He is a farmer. He had a good produce of crops. He does not want to advertise because he is afraid he would have guests at home and he would have to share with them.
2. Sonabai – She too had a good produce. She too like Motiram did not want to advertise because she does not like to have guests.
3. Hirabai – She too feels that guests are pests. She hates to give food and money to others.
4. Rupabai – She thinks a little differently. She feels it is not right to refuse someone who comes for help.
5. Traveller – He is a traveller who has travelled a long distance and is tired and hungry. He hears the conversation of the villagers and comes to know that they are miserly. In the end he makes everyone contribute a little towards making of the soup.

Question c.
How do the following avoid giving anything to the traveller?
Answer:
Motiram – He tells the traveller that dinner was over and nothing was left. He tells the traveller to try elsewhere.
Sonabai – She pretended to be hard of hearing which eventually made the traveller try elsewhere.
Hirabai – She pretended not to understand the traveller’s language and spoke gibberish (nonsense) which made the traveller try elsewhere.
Rupabai – She told the traveller that she too was very hungry because she had not made anything as her larder was empty.

Question d.
Find what Hirabai tells the traveller by reading her words from right to left.
Answer:
Go away. No food and no rest for anyone here.

Question e.
Apart from the stone, how many things go into the soup?
Answer:
Apart from the stone, water, potatoes, carrots, tomatoes, beans, onions, ginger, salt and pepper go into making the soup.

Question f.
Does the traveller really have a magic stone?
Answer:
No, the traveller does not have a magic stone, but he uses the stone to make the miserly villagers believe that the stone was magical.

2. On any one page, note against the speech of every character, what feelings it should show to bring out the meaning best. For example, joy, fear, anger, nervousness, friendliness, dislike, surprise, wonder, excitement, politeness, rudeness, cunning, curiosity.

Question 1.
On any one page, note against the speech of every character, what feelings it should show to bring out the meaning best. For example, joy, fear, anger, nervousness, friendliness, dislike, surprise, wonder, excitement, politeness, rudeness, cunning, curiosity.
Answer:

1. Rupabai – surprise, wonder
2. Traveller – regret
3. Rupabai – cunning
4. Traveller – joy, expectation
5. Rupabai – unsure
6. Sonabai – friendliness
7. Hirabai – apologetic

3. Read aloud / Enact the play.

Question 1.
Read aloud / Enact the play.

4. Write a recipe for the stone soup.

Question 1.
Write a recipe for the stone soup.
Answer:
The Stone Soup
Once upon a time a tired and weary traveller came to a village. The Sun had just set. The traveller was very hungry and very tired. He hoped to get food and shelter in the village. He saw cottages in a row and walked towards them when suddenly he heard voices of people chatting. He stopped to hear ….
Now can you continue with the story.

5. Form pairs. Write at least one short dialogue for each of the following expressions.

Question 1.
Form pairs. Write at least one short dialogue for each of the following expressions.
(a) I agree (b) True! (c) You are right (d) Why not? (To mean that something can be done) (e) Thank you
Answer:
For example:
(a) Amit: I think all schools should have big playgrounds.
Sumit: I agree!

(b) Mohit: It has been raining cats and dogs.
Rohit: True!

(c) Sangeeta: There is a solution to every problem.
Neeta: You are right.

(d) William: Will I be able to complete this project all by myself?
Mother: Why not?
Rohini: Here are the English notes you wanted.
Sohini: Thank you

6. Find the meaning of ‘Charity begins at home/ Find other sayings which have a similar meaning.

Question 1.
Find the meaning of ‘Charity begins at home/ Find other sayings which have a similar meaning.
Answer:
‘Charity begins at home.’ The meaning of this proverb is – A person’s first responsibility is to look after the needs of their own family and friends.
Saying with similar meanings.

1. Charity and beating begins at home – John Fletcher.
2. Home is where the heart is.
3. Home sweet home.
4. A home away from home.

Now you add some more.

7. List five questions from the play which can be answered with ‘yes’ or ‘no’.

Question 1.
List five questions from the play which can be answered with ‘yes’ or ‘no’.
Answer:
(a) Does it melt away?
(b) Have you guessed the secret of the stone soup?
(c) Do you think that is right?
(d) Can I have some food?
(e) Anyone at home?

8. Smart Answers: Form a large group. Each person asks the next one a question to get him to say ‘yes’ or ‘no’. He/She can use appropriate statements, requests or even other questions as a response. But if he/she says ‘yes’ or ‘no’, he/she is out. Otherwise he/she continues the game. Questions cannot be repeated.

Question 1.
Smart Answers: Form a large group. Each person asks the next one a question to get him to say ‘yes’ or ‘no’. He/She can use appropriate statements, requests or even other questions as a response. But if he/she says ‘yes’ or ‘no’, he/she is out. Otherwise he/she continues the game. Questions cannot be repeated.
Answer:
To be done by students.

9. Visit a library: Find stories about hosts and guests. Share them with the class. Classify the stories into funny and serious stories.

Question 1.
Visit a library: Find stories about hosts and guests. Share them with the class. Classify the stories into funny and serious stories.
Answer:
To be done by students.

Class 6 English Chapter 3.3 Stone Soup Important Questions and Answers

Reading Skills, Vocabulary and Grammar

Read the extract and answer the following questions.

Question 1.
State whether the following statements are true or false.
a. Rupabai thought differently.
b. The villagers notice the traveller when they were chatting outside Motiram’s house.
Answer:
a. True
b. False

Question 2.
What time of the day was it when the villagers were chatting?
Answer:
It was evening time when the villagers were chatting.

Question 3.
What did Hirabai think of guests?
Answer:
Hirabai thought of guests as nuisance.

Question 4.
Uninvited guests are pests according to (Choose the correct alternative)
(a) Sonabai
(b) Hirabai
(c) Motiram
(d) Rupabai
Answer:
(b) Motiram

Question 5.a.
Add a prefix to get the opposite of Polite
Answer:
Impolite

Question b.
Guests can be a nuisance. (Pick out the modal verb and add a question tag)
Answer:
Modal verb – can Guests can be a nuisance, can’t they?

Question c.
Uninvited guests are pests. (Frame a ‘Wh’ question to get the underlined word as the answer)
Answer:
What are uninvited guests?

Question d.
I never waste good food. (Identify the kind of sentence)
Answer:
Assertive/Declarative – Negative

Question e.
You are right. (Change into negative)
Answer:
You are not wrong.

Personal Response:

Question 1.
Should we help people in need? Justify.
Answer:
Yes, we should help people in need if we can. Helping others will surely give us satisfaction and we will feel happy. The person whom we help also is happy. We should remember the saying ‘What goes around comes around.’

Language Study

Do as directed.

Question 1.
Who are you, young man? (Kind of sentence)
Answer:
Interrogative sentence

Question 2.
I am not defeated. (Make it affirmative)
Answer:
I am undefeated.

Question 3.
I can hardly believe this. (Pick out the modal auxiliary)
Answer:
Modal auxiliary – can

Question 4.
I have not seen you around. (Add a question tag)
Answer:
I have not seen you around, have I?

Question 5.
I’m a poor, footsore traveller. (Pick out the adjectives)
Answer:
Adjectives – poor, footsore.

Question 6.
You can taste the goodness of fresh vegetables. (Frame a ‘wh’ question to get the underlined words as the answer)
Answer:
What can you taste?

Question 7.
It reminds me of the soup I had made some time ago. (Change the verb into past perfect)
Answer:
It had reminded me of the soup I had made some time ago.

Student’s Activity:

Question 1.
Write a simple recipe of your choice. Remember:
(a) Ingredients
(b) Method
Answer:
To be done by students.

Stone Soup Summary in English

The play ‘Stone Soup’ revolves around selfish and miserly villagers, Motiram, Sonabai, Hirabai and Rupabai and a traveller. The villagers who have their cottages closeby are discussing about people who come uninvited. They do not like to have guests, more so uninvited ones. A traveller weary and hungry enters their village and tries asking for help, but each of the villagers give some excuse not to help the travellers. In the end the traveller plays a trick on the miserly villagers, brings out a magic stone and prepares a wonderful soup, that too with things (vegetables/ items) given by the villagers themselves.

Introduction:

The play ‘Stone Soup’ is a humorous play. It is actually an old folk tale in which a hungry traveller tricks the miserly villagers into believing that soup can be made from a stone. As the pot of water boils with the stone in it, he urges the villagers, one by one, to add more and more ingredients until the soup becomes a feast fit for a king. This play tries to tell us, that when people share resources, no matter how small each contribution is, the result will always benefit all.

Glossary:

1. footsore (adj) – having painful feet from much walking
2. gibberish (n) – speech or writing that is meaningless
3. larder (n) – a cool room in a house where food is stored
4. tempting (adj) – appealing, attractive, inviting
5. speechless (adj) – not knowing what to say
6. generosity (n) – giving in plenty
7. marvellous (adj) – extremely good or pleasing
8. noble (adj) – having high moral principles
9. hard of hearing (phr) – not able to hear well
10. charity begins at home (proverb) – a person’s first responsibility is to look after the needs of their own family and friends

Balbharti Maharashtra State Board Class 6 Hindi Solutions Sulabhbharati पुनरावर्तन १ Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Hindi Solutions पुनरावर्तन १

Hindi Sulabhbharti Class 6 Solutions पुनरावर्तन १ Textbook Questions and Answers

Question 1.
वर्णमाला सुनाओ और विशेष वर्गों के उच्चारण पर ध्यान दो ।
Answer:
अ आ इ ई उ ऊ ऋ ए ऐ ओ औ अं अः अँ ऑ
क ख ग घ ङ
च छ ज झ ञ
ट ठ ड ढ ण (ड़ ढ़)
त थ द ध न
प फ ब भ म
य र ल व श ष स ह
क्ष त्र ज्ञ श्र

Question 2.
विद्यालय के स्नेह सम्मेलन का वर्णन करो।
Answer:
मेरे विद्यालय में प्रत्येक वर्ष स्नेह सम्मेलन मनाया जाता है। इस वर्ष स्नेह सम्मेलन के मुख्य अतिथि थे, पुणे विश्वविद्यालय के उपकुलपति! उनका स्वागत लेझिम नृत्य द्वारा किया गया। प्राथमिक विभाग के विद्यार्थियों ने स्वागत-नृत्य प्रस्तुत कर सभी अतिथियों का मन मोह लिया। माध्यमिक विभाग के विद्यार्थियों ने देश के विभिन्न प्रांतों का लोकनृत्य दिखा कर समा बाँध दिया। उच्च माध्यमिक विभाग के विद्यार्थियों ने हिंदी और मराठी में देशभक्ति पर नाटक प्रस्तुत किए। प्रधानाध्यापक ने विद्यार्थियों को पुरस्कार दिए। इस अवसर पर विद्यार्थियों के साथ-साथ उनके माता-पिता भी उपस्थित थे। इस तरह इस वर्ष भी बड़े धूम-धाम से स्नेह सम्मेलन मनाया गया।

Question 3.
पसंदीदा विषय पर विज्ञापन बनाकर उसको पढ़ो।
Answer:

Question 4.
फल-फूलों के दस-दस नाम लिखो।

Answer:

फलों के नाम:

१.अनार
२. आम
३. अमरूद
४. केला
५. खरबूजा
६. चीकू
७. जामुन
८. मोसंबी
९. तरबूज
१०. संतरा

फूलों के नाम:

१. कमल
२. कनेर
३. गुलाब
४. गेंदा
५. गुड़हल
६. चमेली
७. चंपा
८. जूही
९. पलाश
१०. मोगरा

Question 5.
अक्षर समूह में से खिलाड़ियों के नाम बताओ और लिखो।

Answer:

1. साइना नेहवाल
2. ध्यानचंद
3. खाशाबा जाधव
4. मिल्खा सिंह
5. मेरी कॉम
6. सानिया मिर्जा
7. सचिन तेंडुलकर

Balbharti Maharashtra State Board Class 6 Marathi Solutions Sulabhbharati Chapter 14 अप्पाजींचे चातुर्य Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 6 Marathi Solutions Chapter 14 अप्पाजींचे चातुर्य

Marathi Sulabhbharti Class 6 Solutions Chapter 14 अप्पाजींचे चातुर्य Textbook Questions and Answers

1. एका वाक्यात उत्तर लिहा.

प्रश्न अ.
अप्पाजींनी बैलगाडीत कशाचे पीक घ्यायला लावले?
उत्तर:
अप्पाजींनी बैलगाडीत कोबीचे पीक घ्यायला लावले.

प्रश्न आ.
उत्कृष्ट दर्जाची मूर्ती कोणती?
उत्तरः
ज्या मूर्तीच्या कानात घातलेली तार तेथेच अडून राहिली, ती तिसरी मूर्ती उत्कृष्ट दर्जाची होय.

प्रश्न इ.
कलिंगचा राजा संतुष्ट का झाला?
उत्तरः
अप्पाजींनी तीनही मूर्तीचा दर्जा बरोबर ओळखल्याने कलिंग राजा संतुष्ट झाला.

2. तीन – चार वाक्यांत उत्तरे लिहा.

प्रश्न अ.
अप्पाजींनी ताजी कोबी कलिंग देशाकडे कशी पाठवली?
उत्तरः
राजाने अप्पाजींच्या सांगण्याप्रमाणे एका गाडीत माती भरून त्यात कोबीच्या बिया पेरून ती कलिंग राज्याकडे रवाना केली. गाडीवान प्रवासात रोज कोबींच्या रोपांना पाणी देत असे. तीन महिन्यांनी ती बैलगाडी कलिंग राज्यात पोहचली. अशाप्रकारे कलिंग राजाला ताजी कोबी मिळाली.

प्रश्न आ.
कलिंगच्या राजाने अप्पाजींची दुसऱ्यांदा कशी परीक्षा घेतली?
उत्तरः
कलिंगच्या राजाने दुसऱ्यांदा एकसारख्या दिसणाऱ्या तीन मूर्ती मागवल्या व म्हणाला, ‘या तीनही मूर्ती दिसायला सारख्या असल्या, तरी यांतली एक मूर्ती निकृष्ट आहे, दुसरी मध्यम दर्जाची आहे आणि तिसरी उत्कृष्ट आहे. या सारख्या दिसणाऱ्या तीन मूर्तीमधील उत्कृष्ट कोणती ते मला
सांगा.’

अप्पाजींनी एक लवचिक तार घेतली. ती पहिल्या मूर्तीच्या कानात घातली. ती तार मूर्तीच्या तोंडातून बाहेर पडली. अप्पाजी म्हणाले, ‘ही निकृष्ट मूर्ती आहे! नंतर अप्पाजींनी ती तार दुसऱ्या मूर्तीच्या कानात घातली. ती तार त्या मूर्तीच्या दुसऱ्या कानातून बाहेर पडली. अप्पाजी म्हणाले, ‘ही मध्यम दर्जाची मूर्ती होय.’ तिसऱ्या मूर्तीवरही अप्पाजींनी हाच प्रयोग केला. त्या मूर्तीच्या कानात घातलेली तार तिच्या तोंडातून वा दुसऱ्या कानातून कोठूनच बाहेर पडली नाही. अप्पाजी म्हणाले, ‘ही उत्कृष्ट मूर्ती.’ अशा प्रकारे परीक्षा घेतली.

प्रश्न इ.
मूर्तीच्या तोंडात घातलेली तार तोंडातून बाहेर येते याचा अप्पाजींनी कोणता अर्थ लावला?
उत्तरः
एखादा माणूस ज्या अफवा ऐकतो, त्याचा खरेखोटेपणा पडताळून न पाहता जर तो त्या दुसऱ्यांना सांगू लागला, तर त्याचे व समाजाचेही हित होत नाही. असा अर्थ मूर्तीच्या कानात घातलेली तार तोंडातून बाहेर पडलेल्या मूर्तीबद्दल सांगितला.

प्रश्न ई.
अप्पाजींच्या मते उत्तम माणूस कोणता?
उत्तरः
अफवा ऐकल्यावर जो माणूस दुसऱ्या कानाने ती सोडून देत नाही किंवा लगेच ती दुसऱ्याला सांगत नाही, तर तिच्या खरेखोटेपणाची खात्री करून घेतो आणि आपण काय ऐकले ते पुराव्याशिवाय सांगत नाही, तो माणूस उत्तम. असे अप्पाजींचे मत आहे.

3. पाणी टंचाईमुळे तुम्हांला पाणी दुरून आणायचे आहे. कमी श्रमात ते आणण्यासाठी तुम्ही काय प्रयत्न कराल?

प्रश्न 1.
पाणी टंचाईमुळे तुम्हांला पाणी दुरून आणायचे आहे. कमी श्रमात ते आणण्यासाठी तुम्ही काय प्रयत्न कराल?

4. विरूद्धार्थी शब्द लिहा.

प्रश्न 1.
विरूद्धार्थी शब्द लिहा.
उत्तरः
(अ) हित × अहित
(आ) निकृष्ट × उत्कृष्ट

5. खाली दिलेल्या उदाहरणाप्रमाणे चौकट पूर्ण करा.

प्रश्न 1.
खाली दिलेल्या उदाहरणाप्रमाणे चौकट पूर्ण करा.

उत्तरः

गाडी – गाडीवान	चतुर – चतुराई	खरा – खरेपणा
धन – धनवान	महाग – महागाई	साधे – साधेपणा
दया – दयावान	स्वस्त – स्वस्ताई	शहाणा – शहाणपणा
बल – बलवान	नवल – नवलाई	भोळा – भोळेपणा

6. खालील शब्द वाचा व समजून घ्या.

प्रश्न 1.
खालील शब्द वाचा व समजून घ्या.
उत्तर:

1. चतुर – चातुर्य
2. चोरी – चौर्य
3. क्रूर – कौर्य
4. शूर – शौर्य
5. सुंदर – सौंदर्य
6. धीर – धैर्य

7. खालील शब्दांना तो, ती, ते शब्द लावून लिंग ओळखा.

प्रश्न 1.

1. दरी
2. पान
3. पुस्तक
4. माठ
5. लाडू
6. वही

उत्तर:

1. ती दरी – स्त्रीलिंग
2. ते पान – नपुंसकलिंग
3. ते पुस्तक – नपुंसकलिंग
4. तो माठ – पुल्लिंग
5. तो लाडू – पुल्लिंग
6. ती वही – स्त्रीलिंग

8. तुमच्या मित्राच्या / मैत्रिणीच्या चतुरपणाचे कौतुक झाल्याचा प्रसंग घरी व वर्गात सांगा.

प्रश्न 1.
तुमच्या मित्राच्या / मैत्रिणीच्या चतुरपणाचे कौतुक झाल्याचा प्रसंग घरी व वर्गात सांगा.
उत्तर:
आज रस्त्याने जात असता एक तरूण मुलगा कानात हेडफोन घालून मोबाईलची गाणी ऐकत रस्ता पार करत होता. त्याने डावी व उजवीकडे गाडी येताना पाहिलेच नाही. तेवढ्यात समोरून एक सुसाट गाडी येताना माझ्या मित्राला दिसली. ती गाडी सतत हॉर्न वाजवत होती, पण त्याच्या कानावर तो आवाज गेला नाही. आता अपघात होणारच होता एवढ्यात माझ्या तनय नावाच्या मित्राने समयसुचकता दाखवून त्याला पटकन मागे ओढले. म्हणून तो अपघात टळला. तनयचे कौतुक करावे तेवढे थोडेच.

9. अप्पाजींसारख्या अनेक चतुर व्यक्ती इतिहासात होऊन गेल्या आहेत. उदा., बिरबल, तेनालीराम. यांच्या गोष्टी मिळवा. वाचा. वर्गात सांगा.

प्रश्न 1.
अप्पाजींसारख्या अनेक चतुर व्यक्ती इतिहासात होऊन गेल्या आहेत. उदा., बिरबल, तेनालीराम. यांच्या गोष्टी मिळवा. वाचा. वर्गात सांगा.

10. खालील वेबमध्ये दिलेल्या शब्दांस विशेषणे लावा.

प्रश्न 1.

उत्तरः

1. चवदार कोबी
2. बेचव कोबी
3. ताजी कोबी
4. शिळी कोबी

प्रश्न 2.

उत्तरः

1. मातीची मूर्ती
2. देखणी मूर्ती
3. सजवलेली मूर्ती
4. सुंदर मूर्ती

खालील तक्ता वाचा. समजून घ्या.

प्रश्न 1.

उत्तर:

वतमान काळ	भूतकाळ	भविष्य काळ
1. माया खेळते	माया खेळली	माया खेळेल
2. तो खेळतो	तो खेळला	तो खेळेल
3. तुम्ही खेळता	तुम्ही खेळलात	तुम्ही खेळाल
4. आम्ही खेळतो	आम्ही खेळलो	आम्ही खेळू
5. त्या खेळतात	त्या खेळल्या	त्या खेळतील

दिलेल्या सूचनांप्रमाणे खालील वाक्यांत बदल करा.

प्रश्न 1.
रिमा सहलीला गेली. (भविष्यकाळ करा)
उत्तर:
रिमा सहलीला जाईल.

प्रश्न 2.
मला आंबा आवडतो. (भूतकाळ करा)
उत्तर:
मला आंबा आवडला.

प्रश्न 3.
चंदाने लाडू खाऊन संपवला. (वर्तमानकाळ करा)
उत्तर:
चंदा लाडू खात आहे.

प्रश्न 4.
सुभाष माझा मित्र आहे. (भूतकाळ करा)
उत्तर:
सुभाष माझा मित्र होता.

प्रश्न 5.
वंदना अभ्यास करते. (भूतकाळ करा)
उत्तर:
वंदनाने अभ्यास केला.

प्रश्न 6.
संजू क्रिकेट खेळतो. (भविष्यकाळ करा)
उत्तर:
संजू क्रिकेट खेळेल.

पूर, गाव, नगर,बाद ही अक्षरे असणाऱ्या गावांची, शहरांची, ठिकाणांची नावे खालील तक्त्यात लिहा.

प्रश्न 1.
पूर, गाव, नगर,बाद ही अक्षरे असणाऱ्या गावांची, शहरांची, ठिकाणांची नावे खालील तक्त्यात लिहा.

उत्तर:

गाव	पूर	नगर	बाद
1. मानगाव	सोलापूर	अहमदनगर	औरंगाबाद
2. नागाव	कोल्हापूर	सह्याद्रीनगर	दौलताबाद
3. सोनगाव	नागपूर	संभाजीनगर	उस्मानाबाद
4. भरतगाव	कानपूर	हनुमाननगर	फिरोजाबाद
5. धरणगाव	राजापूर	वैभवनगर	अहमदाबाद
6. शेगाव	तारापूर	जामनगर	हैद्राबाद

Class 6 Marathi Chapter 14 अप्पाजींचे चातुर्य Additional Important Questions and Answers

खालील प्रश्नांची प्रत्येकी एक-दोन वाक्यांत उत्तरे लिहा.

प्रश्न 1.
कृष्णदेवराय कोणत्या नगराचा राजा होता?
उत्तरः
कृष्णदेवराय विजयनगरचा राजा होता.

प्रश्न 2.
विजयनगरच्या प्रधानाचे नाव काय होते?
उत्तरः
विजयनगरच्या प्रधानाचे नाव अप्पाजी होते.

प्रश्न 3.
उत्तरकडे कोणते राज्य होते?
उत्तरः
उत्तरेकडे कलिंग राज्य होते.

प्रश्न 4.
त्या काळी वाहतूक कशातून होत असे?
उत्तरः
त्या काळी बैलगाडीतून वाहतूक होत असे.

प्रश्न 5.
बैलगाड्या कलिंग राज्यात पोहचायला किती महिने लागत?
उत्तरः
बैलगाड्या कलिंग राज्यात पोहचायला तीन महिने लागत.

प्रश्न 6.
कलिंग राजाने एकूण किती मूर्त्या आणल्या?
उत्तरः
कलिंग राजाने एकूण तीन मूर्त्या आणल्या.

प्रश्न 7.
निकृष्ट दर्जाची मूर्ती कोणती?
उत्तरः
मूर्तीच्या कानातून घातलेली तार मूर्तीच्या तोंडातून बाहेर पडली ही निकृष्ट दर्जाची मूर्ती होय.

प्रश्न 9.
मध्यम दर्जाची मूर्ती कोणती?
उत्तर:
ज्या मूर्तीच्या एका कानातून घातलेली तार दुसऱ्या कानातून बाहेर पडली ती मूर्ती मध्यम दर्जाची होय.

व्याकरण व भाषाभ्यास

प्रश्न 1.
खालील शब्दांचे समानार्थी शब्द लिहा.

1. जुनी
2. गोष्ट
3. चतुर
4. राजा
5. निरोप
6. निकृष्ट
7. उत्कृष्ट
8. कान
9. माणूस
10. खात्री
11. संतुष्ट
12. पुरावा

उत्तर:

1. पुराणी
2. कथा
3. हुशार
4. नृप
5. सांगावा
6. तकलादू
7. चांगली
8. कर्ण
9. मनुष्य
10. विश्वास
11. समाधानी
12. दाखला

प्रश्न 2.
खालील शब्दांचे विरूद्धार्थी शब्द लिहा.

1. जुनी
2. उत्तर
3. प्रश्न
4. चतुर
5. चवदार
6. इच्छा
7. जलद
8. ताजी
9. सारखा
10. बाहेर
11. माणूस
12. खरे
13. नुकसान

उत्तर:

1. नवी
2. दक्षिण
3. उत्तर
4. मुर्ख
5. बेचव
6. अनिच्छा
7. सावकाश
8. शिळी
9. वेगळा
10. आत
11. स्त्री
12. खोटे
13. फायदा

अप्पाजींचे चातुर्य Summary in Marathi

पाठपरिचय:

विजयनगरमध्ये असणाऱ्या कृष्णदेवरायच्या राज्यात त्याचे प्रधान अप्पाजी फार चतुर होते. उत्तरेकडे असलेल्या कलिंग राजाने अप्पाजींची चतुराई कशी पारखली, त्याच्या परीक्षेला अप्पाजींनी कसे कौशल्याने तोंड दिले याचे वर्णन या पाठात आले आहे.

शब्दार्थ:

1. चातुर्य – हुशारी (cleverness)
2. जुनी – प्राचीन (Many year’s ago)
3. प्रधान – मंत्री (Minister)
4. उत्तर – North
5. चतुराई – हुशारी (cleverness)
6. निरोप – संदेश (Message)
7. चवदार – रुचकर (tasty)
8. कोबी – एक फळभाजी (cabbage)
9. आस्वाद – चव (taste, flavour)
10. त्या काळी – त्या वेळी (that time)
11. जलद – गतीमान (fast)
12. साधने – वाहने (vehicle)
13. बैलगाडी – Bullock cart
14. राज्य – state
15. ताजी – Fresh
16. कुजून – सडून (rotten)
17. गाडीवान – गाडी चालवणारा, वाहक (Driver)
18. बी – बीज (seed)
19. पेरणे – जमिनीत बी टाकणे (sowing)
20. रवाना – पाठवणे (to send)
21. कौतुक – प्रशंसा (to admire)
22. परीक्षा – कसोटी (test)
23. एकसारख्या – समान, सारख्या (same)
24. मूर्ती – प्रतिमा (Statue)
25. निकृष्ट – कमी दर्जाची (in ferier)
26. उत्कृष्ट – उत्तम (superior, excellent)
27. लवचिक – हलणारी (Flexible)
28. तार – धातूचा तंतू (wire)
29. अफवा – खोटी बातमी (rumour)
30. हित – कल्याण, भले (interest)
31. नुकसान – तोटा (Loss)
32. संतुष्ट – समाधानी (satisfied)
33. पुरावा – दाखला (proof, evidence)

वाक्प्रचार व अर्थ:

1. चतुराई पाहणे – हुशारी पाहणे
2. परीक्षा घेणे – कौशल्य तपासून पाहणे
3. खरेखोटेपणा पडताळणे – सत्य, असत्य तपासणे
4. हित नसणे – भले नसणे, कल्याण नसणे
5. अफवा ऐकणे – खोटी बातमी ऐकणे.
6. खात्री करणे – तपासून, चौकशी करणे